一维离散型核函数的神经场稳态解的研究

况发伦，杨慕容，金德泉

(广西大学数学与信息科学学院，广西南宁530004)

0 引言

哺乳动物的大脑神经皮质是高度发达的神经系统，神经系统在数学上可以抽象成一类拥有激励模式的信息处理中心的神经场。20世纪70年代，科学家提出了很多不同的神经场模型描述大脑皮层神经元之间的兴奋活动[1-5]。在这些模型中，Amari的动力神经场模型描述的是具有相同功能和性质的皮质神经元在兴奋时相互作用所表现出的在统计学的行为，可以用于分析两个神经场之间地形连接的形成机制，并且能够很好的解决一些神经生理学问题和解释一些重要的神经物理学现象[6]。在实际运用中，Amari的动力神经场方程稳态解的性质往往决定有很大的作用，如在聚类中[7-8]，局部解可以看成是连接数据模型的边界，边界的位置影响数据集分类的好坏，所以局部解的性质决定了数据聚类结果的优劣。研究稳态解的性质不仅丰富了神经场模型的理论，同时增加了神经场模型应用的广度，如粒计算[9]、信息几何[10]等。

神经场模型的稳态解的相关性质也被众多学者讨论过[11-13]，笔者讨论的是在一维离散型核函数条件下，神经场模型稳态解的存在性和一些性质，得到了三种类型稳态解(φ解，局部解，∞解)存在的条件，并给出了在特定条件下，局部解半径的求法，分析了此条件下局部解的稳定性质。

1 神经场方程

考虑一维的Amari的动力神经场方程：

(1)

τ>0表示时间常数，Ω表示感知区域，h≥0表示神经场的静息水平，s(x,t)表示输入信号分布函数。u(x,t)表示时间为t位于x的神经元的平均膜电位，u(x,t)可以视为x与t的可微函数，{x∈Ω:u(x,t)>0}表示兴奋区域。假设神经元在x与t时的平均活动，即脉冲发射率，由u(x,t)的函数给定θ(u(x,t))，θ(u)是单调递增的非线性阈值函数，满足:

(2)

θ(u)描述的是神经场兴奋区域Ω内的一点与其邻域的反馈，在很多情况下，离散型阈值函数取阶跃函数:

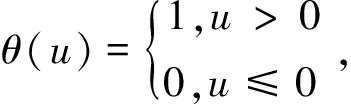
(3)

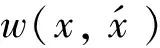
(4)

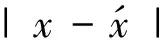
由于本文讨论的重点是离散型核函数的神经场方程的稳态解，所以假定输入函数是时不变的，即s(x,t)=s(x)≥0。

令Ω=R，则有:

(5)

由于神经元的激活机制的特性，w(x)是各向同性函数，其形状是“墨西哥帽”形，函数基本形式为:

(6)

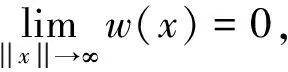
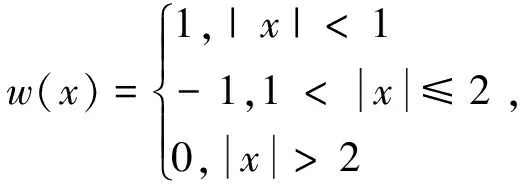
(7)

令:

(8)

则神经场方程(5)的所有稳态解u*(x)均满足F(u*(x))=0。

定义若u*(x)是神经场方程的稳态解[12]，即:

(9)

则有:

(10)

①若∀x∈R，u*(x)≤0，则u*(x)为φ解;

②若∀x∈R，u*(x)>0，则u*(x)为∞解;

③D∈R且D为一对称区域，当x∈D时，u*(x)>0；当x∉D时，u*(x)≤0，则u*(x)为局部解;

说明方程只存在φ解，说明兴奋区域不存在；只存在∞解，说明区域全局兴奋；若方程存在局部解，则说明神经场存在局部兴奋区域。

另设wmin(x)=min{w(x),0}，wmax(x)=max{w(x),0}，

则有:

(11)

(12)

(13)

设输入函数s(x)有界，则存在S0>0，s0>0，使得:

s0≤s(x)≤S0。

(14)

2 主要结果与证明

假设交互核w(x)满足式(12)、(13)，s(x)满足式(14)。

命题1若S0-h+1≤0，则式(5)的稳态解均为φ解；若存在φ解，则s0-h≤0。

证明∀x∈R，阈值函数为θ(u)∈[0,1]，令F(u*(x))=0，则:

1+S0-h≤0,

(15)

所以，根据φ解的定义，当S0-h+1≤0时，原方程所有稳态解均为φ解。

若∀x∈R，令F(u*(x))=0，则:

=s0-h。

(16)

由于φ解存在，则s0-h≤u*(x)≤0，即s0-h≤0，证毕。

命题2当输入函数s(x)=0时，动力神经场方程(5)存在唯一的φ解u*(x)=-h。

证明令u*(x)=-h，此时阈值函数θ(u*(x))=θ(-h)=0，则：

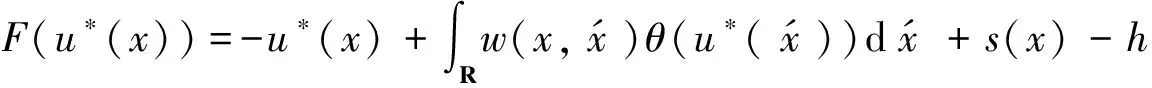
(17)

所以u*(x)=-h是神经场方程(5)的稳态解。

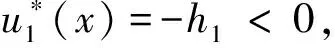
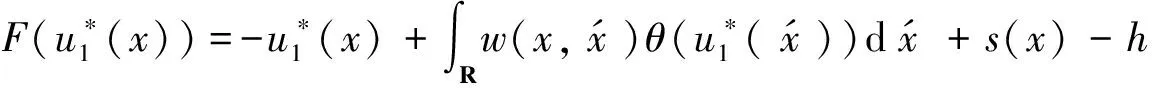
(18)

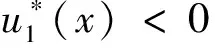
命题3若s0-h>0，则式(5)的稳态解均为∞解；若存在∞解，则S0-h+1>0。

证明∀x∈R，阈值函数θ(u)∈[0,1]，令F(u*(x))=0，则：

=s0-h>0。

(19)

所以，根据∞解的定义，当s0-h>0时，原方程所有稳态解均为∞解。

若∀x∈R，令F(u*(x))=0，则：

=1+S0-h。

(20)

由于∞解存在，则1+S0-h>u*(x)>0，即1+S0-h>0，证毕。

推论1θ(u)∈[0,1]为所给定单位阶跃函数，若神经场方程(5)存在局部解，则S0-h+1>0且s0-h≤0。

证明∀x∈R，令F(u*(x))=0，有：

1+S0-h≥u*(x)≥s0-h。

(21)

根据局部解的定义，若方程存在局部解，需保证s0-h≤0且S0-h+1>0，证毕。

现假设D={x∈R:00，令：

(22)

当x=d时，令：

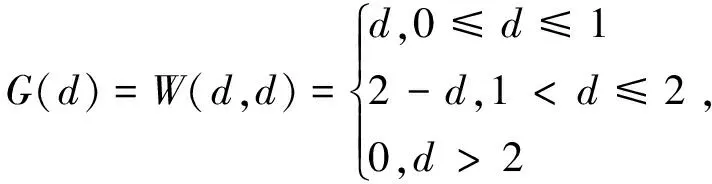
(23)

(24)

(25)

命题4当输入函数s(x)=0时，G(d)-h=0是动力神经场方程(5)存在局部解的充分必要条件。

证明充分性。由于神经场方程(5)存在局部解，根据式(22)、(23)中G(d)的定义，局部解必满足G(d)-h=0。

下证必要性。与文献[14]的证明类似，由于G∞=0，G(0)=0，而G(d)连续有界，由零点定理可知，当G(d)-h=0时，方程(5)必存在局部解。

命题5假设输入函数s(x)=0，若G∞

证明当输入函数s(x)=0，x=d时，则：

u*(d)=G(d)-h，

(26)

根据式(23)，可得d1=h、d2=2-h。此时区域D=[h,2-h]。

采用邻域分析法证明局部解的稳定性：

对于u*(d1)，u*(d1-Δd)<0，∂u-/∂t<0，而u*(d1+Δd)>0，∂u+/∂t<0，故u*(d1)为不稳定的局部解。

对于u*(d2)，u*(d2-Δd)>0，∂u-/∂t>0，而u*(d2+Δd)<0，∂u+/∂t<0，故u*(d2)为稳定的局部解，证毕。

说明命题5给出了动力神经场在没有外部输入的短期记忆时，局部解兴奋区间范围的计算方法。

3 结论

本文研究了带有离散型核函数的一维Amari的动力神经场方程稳态解的存在性，得到了三种典型解的存在条件。θ(u)∈[0,1]为单位阶跃函数，假设交互核w(x)满足式(12)和式(13)，s(x)满足式(14)，当S0-h+1≤0时，神经场方程稳态解均为φ解；当s0-h>0时，神经场方程稳态解均为∞解；假设输入函数s(x)=0，则u*(x)=-h是神经场方程存在的唯一φ解，进一步，假设G(d)满足式(23)～式(25)，G(d)-h=0是神经场方程存在局部解的充分必要条件，并且当0