基于预测机制的装配作业重调度问题建模优化

陆志强，方 佳

（同济大学机械与能源工程学院，上海201804）

在实际飞机移动装配线中，装配作业在装配调度计划的指导下依次执行。飞机移动装配线调度问题可抽象成资源受限项目调度问题（resourceconstrained project scheduling problem），近几年的相关研究大多围绕不确定环境展开，Panda等［1］和Liu等［2］均以制造业为背景研究作业时长变动、物料送达不准时等不确定因素影响下的调度问题。对于飞机移动装配这种单件大型复杂产品的装配项目而言，因装配质量不合规格增加的修复操作就是不可忽视的不确定因素之一，它既可能导致后续作业延迟开始也可能造成装配人员安排、资源配送和使用计划发生伴随性变动，装配计划执行过程不稳定性增加的同时企业也将产生额外的计划调整成本。本文从高效性和经济性出发，研究飞机移动装配线中作业因为质量原因被增加修复操作这一环境下的重调度问题。

随着飞机移动装配线越来越多地采用智能设备辅助装配，设备性能衰退逐渐成为影响作业装配质量进而干扰装配计划的要因。Kang等［3］和Liu等［4］都研究制造系统中机器设备“硬故障”（设备彻底不可运行）中断作业这一环境下的调度问题，相比设备“硬故障”，飞机移动装配线中发生设备“软故障”的频繁更高。与Shahkarami等［5］分析的光纤网络软故障（soft-failure）类似，复杂装配系统中机器设备发生“软故障”时虽能运行，但却会导致装配质量问题频繁出现并演变为频繁的作业修复。本文将机器设备中工装夹具、刀具、夹具与刀具构成的部件定义为质量相关部件，它们的磨损与退化是促使设备发生“软故障”的主要因素。本文通过收集设备质量相关部件的衰退以及作业质量特性偏差历史数据构建前端的作业质量预测模型。

现有解决不确定环境下调度问题的方法可以分为前摄调度法和反应调度法。多数研究前摄调度方法的文献通过数学公式推导出可插入调度计划中的缓冲时间值或资源投入量来应对干扰。前摄型调度研究成果中，Cui等［6］针对流水车间故障不确定环境下的生产调度与维护计划联合优化问题，提出了双层循环算法。Tan等［7］将紧急救援问题抽象成了资源受限项目调度问题并设计了一种混合型遗传-禁忌算法。Bruni等［8］研究了作业执行时间不确定的资源受限项目调度问题并提出了自适应的鲁棒优化模型对资源分配作出决策。在反应调度方法的研究中，Qiao等［9］针对半导体制造中的突发事件提出了包含一个规则和一个调度程序的局部快速修复型重调度算法。Creemers等［10］研究作业执行时间随机变动的反应型调度问题并采用马尔科夫链进行动态优化决策。Rahmani等［11］针对动态柔性车间中未预期的新工件到达造成干扰的问题，设定双优化目标并提出了一种变邻域算法生成较稳定的重调度方案。

如今智能制造正通过促进信息通信技术与制造过程的整合来重塑制造业，数据驱动式的决策方式对制造业的未来具有重要意义。本文基于这种思想提出了指导现场实际作业装配的闭环框架，该框架的前端利用预测模型对作业质量进行预测，后端基于预测结果构建重调度模型并运用本文提出的改进型免疫算法调整作业装配计划。

1 问题描述以及数学模型

1.1 问题描述

以飞机移动装配线为背景提出的预测-重调度闭环框架的相关假设与说明如下，其中后端作业重调度模型的内容在1.2节详细描述。

（1）飞机移动装配线当前工位的装配作业集合记作J={1，2，3，...，j，...，N}，其中1和N是虚拟作业；作业j∈J有确定的装配时长tdj和对第k∈K种资源的需求量r jk，K为资源集合；任意作业j受到时序约束必须在其全部紧前作业完成后才能开始；此外，受有限资源量的约束，任意时刻任意种类的资源总需求量不能超过该类资源的供应量R k。

（2）装配作业所需机器设备中共包含ρ类质量相关部件，类型集合记作Q={1，2，3，...ρ}。作业j所需第q∈Q类质量相关部件的衰退情况用夹具长度衰退量l jq、夹具直径衰退量c jq、夹具张紧力衰退量s jq和刀具磨损量g jq构成的向量D jq=(l jq，c jq，s jq，g jq)T表示，D j是维度为4O j的单列向量，其中O j为作业j所需质量相关部件类型总数。Wang等［12］针对衰退型生产系统研究生产与维护联合优化问题时采用gamma过程来描述生产系统退化；Lu等［13］研究串并行多阶段制造系统机会维护问题时，考虑到设备中质量相关部件（QRCs）衰退过程具有随机独立、非负增量的性质故采用gamma过程对QRCs衰退进行建模，同理本文假设作业所需设备中质量相关部件的衰退过程服从gamma过程。任意作业j的初始衰退向量记作Dojq=(lojq，cojq，sojq，gojq)T，Dojq中每个维度都服从正态分布。

（3）为保证飞机装配的质量，作业j完成后必须接受n个质量特性偏差检测，检测时间忽略不计，结果 记 作X j=(b x1，b y1，b z1，b x2，b y2，b z2...b x n，b y n，b z n)T，b x i、b y i和b z i（i∈[1，n]）是作业j的第i个质量特性偏差值在x、y和z3个方向上的分量。若X j各维度均落在标准规格范围内可继续执行后续作业；否则需对作业j添加属性为tdjr=ϑtdj和r jrk=ϑr jk的修复作业jr，jr未完成时作业j所有紧后作业都无法执行。

假设X j的各维度b i∈X j，i=[1，3n]都服从正态分布且装配过程对各维度正态分布的影响可明显体现在均值上，忽略各维度方差σji的细微波动，作业最多进行一次修复便可质量达标。装配现场的数据采集系统每隔一定周期进行一次质量相关部件衰退数据以及质量特性偏差数据的更新与存储。

（4）作业j的装配质量有3个主要影响因素：该作业所需设备中质量相关部件衰退情况、关键紧前作业jb的质量特性偏差和j装配中的噪声量。假设任意作业j有且仅有一个关键紧前作业jb对X j有关键影响。当前工位内的全部关键紧前作业构成激发预测机制的作业列表Jb，时间驱动方式下只要有jb∈Jb完成且质检合格将直接触发后续作业质量特性偏差的预测机制，预测机制运行时间忽略不计；质检不通过则直接采用右移策略插入修复作业计划形成新的调度计划指导装配，此部分不是本文重点故不再赘述。

（5）假设装配现场已提供经优化的预防性维护阈值δ=50%，作业质量合格概率预测值相比标准值下降超过δ时将根据更换零衰退部件的成本与质量合格概率改善程度之比确定性价比最高的维护方式，维护时长为tm，维护结束后相应作业才能开始装配。

（6）离散化时间集合记为T={0，1，2，3...T}，装配项目启动前由遗传算法优化得到初始调度计划Fo，基于Fo经调整形成的新调度计划Fn又可视作下一次计划调整的初始调度计划。

1.2 后端作业重调度符号与数学模型

（1）时间相关符号。T：离散化时刻集合；tm：预防性维护持续时长；tp：预测机制触发时刻即重调度时刻，tp∈T。

（2）资源相关符合。K：有限资源集合；R k：第k类资源的供应量。

（3）作业相关符号。J：工位内装配作业集合；j：J中的任意作业；jr：j对应的修复作业；tdj：作业j的执行时长；r jk：作业j对第k类资源的需求量；w j：作业j实际开始时间偏离初始计划开始时间每单位时间所付成本即作业的权重；W j：作业j所有紧后作业单位时间偏差成本累积和。

（4）调度计划相关符号。Fo（Fn）：初始（新）调度计划方案；tosj（tnsj）：作业j在初始（新）调度计划中的开始时刻。

（5）重调度相关符号。Jstp：tp时刻已开始作业列表；Jntp：tp时刻未开始作业列表；Jmtp：tp时刻接受质量相关部件维护的作业列表；Jptp：tp时刻确定要进行预调度的修复作业列表；Jftp：tp时刻Jntp中未进行修复预调度的作业列表；J tp：tp时刻确定的重调度作业列表；JAj（JBj）：预调度作业确定后，作业j更新后的全部紧后（紧前）作业集合。

（6）决策变量符号。x jt：0-1变量，作业j在t时刻开始取1，否则取0。

（7）数学模型为

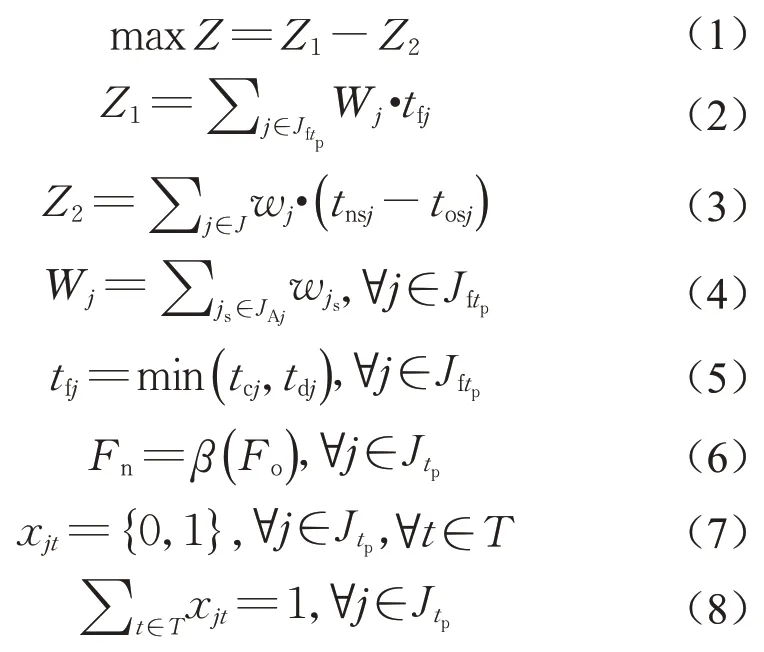
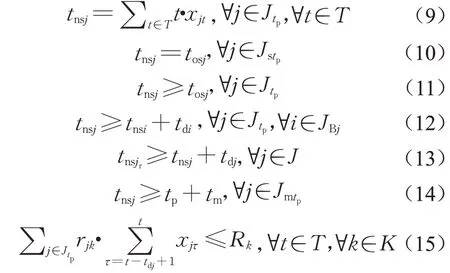
式（1）是优化目标。式（5）tcj是重调度列表中未进行修复预调度的作业在新调度计划中的松弛时间，tcj等于作业j结束时刻到最早紧后开始时刻这段时区中满足资源约束的最大连续时段数，贡献时段tfj取tcj和tdj间的较小值，其含义是一旦j产生了预期外的修复需求且装配现场实施右移策略时作业j所有紧后作业都能少推迟的时间值；式（4）W j是作业j所有紧后作业单位偏差时间需付成本之和；基于式（4）、（5）的式（2）衡量新调度计划中未进行修复预调度的作业应对质量修复干扰时能节约的成本可视为作出的贡献，而式（3）衡量新调度计划相比初始调度计划因作业延迟开始给企业造成的成本支出，因此由式（2）与式（3）的差值构成的优化目标函数（1）的含义是最大化新调度计划对企业的总贡献值。

式（6）-（11）给出了新调度计划（Fn）与初始调度计划（Fo）间的映射与约束关系：Fn是在Fo基础上运用预测和算法得到，但Fn与Fo的对应关系不存在显性表达故直接记作式（6）的β；式（7）-（9）给出了Fn中作业开始时间与决策变量的关系式，同时约束了任意作业只能有一个开始时刻；式（10），（11）则进一步约束了重调度时刻已开始作业的开始时间应与Fo保持一致，重调度作业在Fn中的开始时间不得早于Fo。

最后，式（12）-（15）从时序及资源方面给出了约束：式（12）-（14）从装配工艺时序、装配与修复时序及维护与装配时序角度约束了作业的开始时间；式（15）表示任意时刻作业的资源需求总量不能超过资源的总供应量。

2 整体框架与算法设计

图1是本文构建的实际应用闭环框架。前端离线训练部分主要完成数据的提取、处理和作业质量特性偏差预测模型的训练；后端在线预测部分则主要根据装配线实际数据进行预测并基于预测结果实现装配计划重调度。2.1节、2.3节和2.2节分别对前端模型训练、后端重调度算法以及两者的过渡部分进行了阐述，研究重点仍集中在后端重调度算法的有效性和整体框架的可行性分析上。

图1 实际应用前后端整体框架Fig.1 Front-end overall framework of actual application

2.1 前端支持向量回归（SVR）模型训练

2.1.1 生成训练样本

采用文献［14］基于质量偏差流理论的状态空间模型即公式（16）模拟各作业质量特性偏差的历史数据：

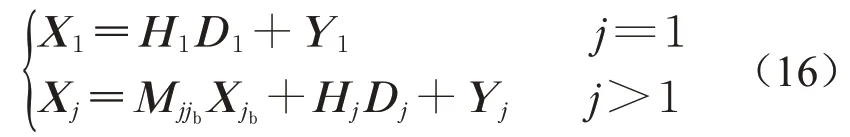
其中，Μjjb是j的关键紧前作业jb与作业j间的质量特性偏差传递矩阵，H j是质量相关部件衰退对作业j质量特性偏差影响的传递矩阵，Y j是噪声矩阵。M jjb、H j和Y j采用文献［14］中的数据。考虑到实际装配现场质量相关部件衰退及作业质量特性偏差在短时间内变化较小故构建训练样本时以数据采集系统数据更新周期为取样周期，作业j的训练样本如（17）矩阵S j所示，S j∈Rs1×s2，其中s2是样本总数。

S j中每个样本的输入矢量I j∈R(3n+4O j)×1由各取样周期内jb的质量特性偏差均值Xmjb以及作业j所需设备的质量相关部件衰退均值Dmj构成，输出矢量E j∈R3n×1等于作业j在周期内的质量特性偏差均值Xmj。

2.1.2 训练支持向量回归模型

对作业质量特性偏差的每一维都建立支持向量回归（SVR）模型，SVR可通过映射函数将非线性问题成功转换为式（18）中高维特征空间的线性回归模型，利用结构风险最小化原则和对偶问题最终可将预测值优化问题表示为（19）［15］：

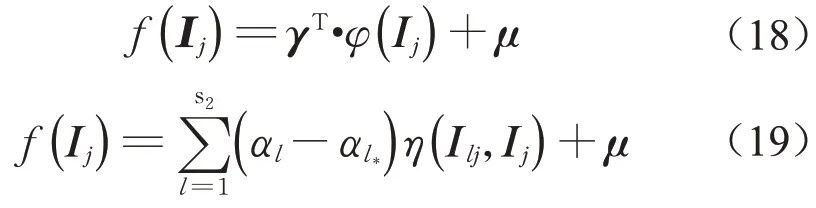
2.2 作业质量预测机制的激发与结果输出

基于2.1节训练的质量特性偏差预测模型，时间驱动下质量预测机制的激发与结果输出流程如下：

步骤1:作业jb∈Jb按计划在tp时刻装配完成并接受质检得到质量特性偏差X jb，考虑到一个数据采集周期内数据都十分接近，故可近似将该值视为当前数据采集周期内的均值Xmjb。

步骤2:确定jb的关键紧后作业列表Jh。遍历Jh，检测jh∈Jh所需设备中质量相关部件的衰退量并基于历史衰退过程预估jh完成时的衰退均值Dmjh，将Xmjb和Dmjh构成矢量Ιjh输入作业jh的预测模型并最终输出jh的质量特性偏差均值预测值Xmjh。由Xmjh以及质量特性偏差的上下规格矢量Xujh和Xdjh通过式（20）可算出jh的合格概率预测值PEjh，若达到预防性维护阈值则将jh纳入Jmtp。

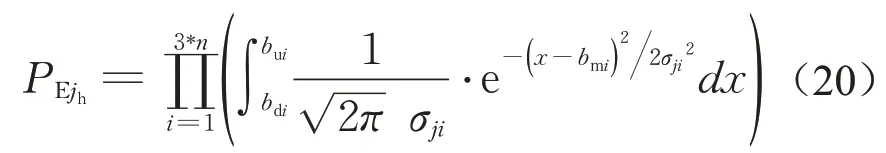
步骤3:tp时刻未开始作业列表Jntp中未被预测的作业质量合格概率默认为历史概率，被预测的作业质量合格概率若是Jntp中的瓶颈，其修复作业将被纳入预调度列表Jptp，Jptp中作业不可多于Nu。

步骤4:重调度作业列表J tp由Jntp和Jptp构成，进一步调用2.3节算法生成装配作业重调度计划。

2.3 改进型免疫算法

免疫算法是一种模仿生物体免疫学机理的较为成熟的启发式算法，本文所提改进型免疫算法（I-IA）重点在种群初始化、交叉变异和种群更新方面进行了改进。

2.3.1 初始种群的生成

为在增加抗体多样性的同时降低转变为完全随机搜索的风险，初始种群L中P条抗体由2种不同的生成方式ξ1(⋅)和ξ2(⋅)按照比例a1和a2构成，记作式（21）：

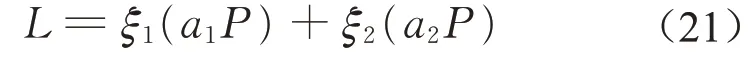
图2给出了局部作业网络结构和运用2种方式生成的抗体编码示例。第1行示意第1种方式，在不违背紧前紧后关系约束的前提下随机生成可行调度编码即抗体；第2行示意第2种方式，编码在不违背作业时序约束的同时被划分为具有一定性质的不同模块，示例被划分的［1］、［3 4］、［8 2 5 7］和［9］这4个模块相互之间位置不可换，但任意一个模块内部的作业相互之间不存在紧前紧后关系，因此可随机交换位置。

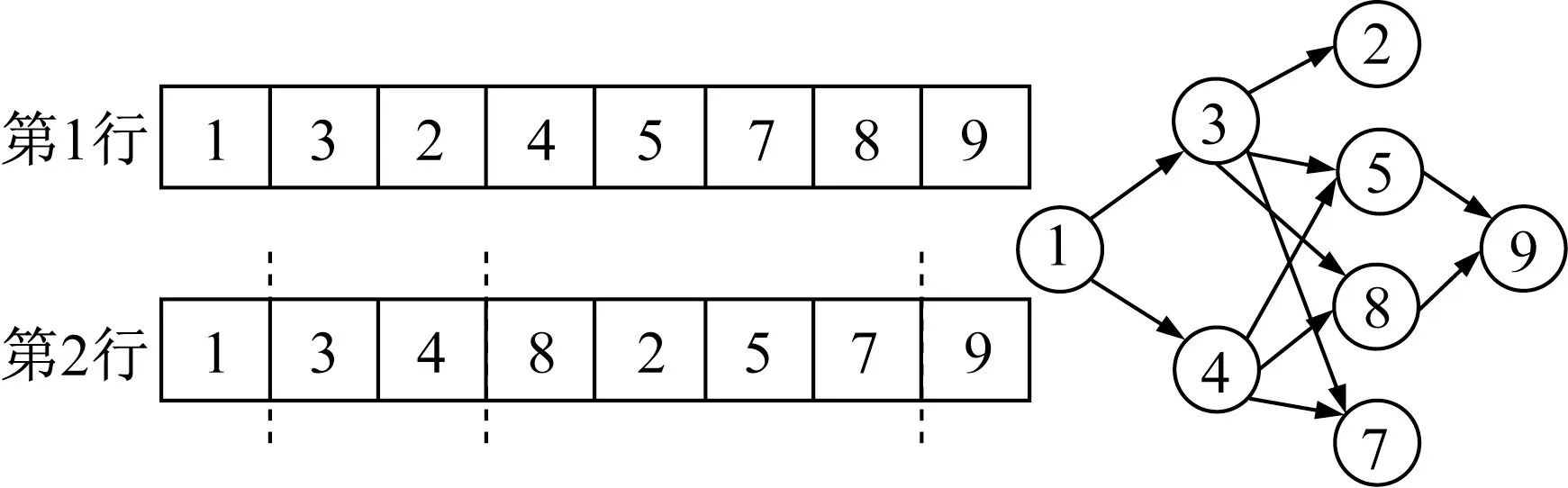
图2 抗体生成方式示例Fig.2 Example of antibody generation methods

当有修复作业被预调度时只需增加修复作业与原作业间的约束关系并更新整体作业网络结构的时序约束关系就可按上述方式生成初始种群。

2.3.2 交叉与变异操作

免疫算法中交叉和变异操作对算法整体性能至关重要。交叉和变异概率越大则抗体被更新的机会越多，这有助于提高种群的多样性但太大的交叉和变异概率也可能使优良基因丢失［16］。在参考文献［17］中交叉变异算子的基础上设计了如下自适应交叉（pc）和变异（pm）算子：

式（22）是方案贡献值也是抗体亲和度评价指标，式（23）、（24）中Ag和As对应2条交叉抗体中较大和较小的亲和度值，Am和Av分别是当前群体的最大与平均亲和度值，Ac是当前抗体的亲和度值。抗体可根据自身亲和度在群体中的表现动态调节交叉或变异概率：亲和度高于群体平均水平的抗体，亲和度越高pm越小，亲和度低于群体平均水平的抗体，亲和度越低pc越大。这种方式可保留较优抗体并有针对性地促使较差抗体进行邻域搜索。此外，本文针对第2种方式生成的抗体设置了简单快速的变异规则：①w j越大的作业调度优先级越高。②W j越大的作业调度优先级越高。③全部紧后作业总数越大的作业调度优先级越高。④随机交换模块中的作业顺序。①-④可针对编码的一个或多个模块实施从而灵活控制变异程度。抗体交叉变异流程如下：

步骤1：按抗体生成方式不同，划分原抗体群为群1和群2，交叉抗体d1、d2需同时源于群1或群2。

步骤2：计算pc并生成随机数r1，若r1≤pc则转步骤3进行交叉，否则不交叉。

步骤3：若d1、d2都来自群2则随机选择2个相邻模块，重新生成2个模块的作业顺序后分别得到子抗体d1s和d2s；若d1、d2都来自群1则随机产生满足h2＞h1的2个位置h1和h2，d1中位置介于h1与h2间的作业按照d2中这些作业的对应顺序排列，其他作业位置不变得到子抗体d1s，同理形成d2s并最终根据亲和度大小更新d1、d2。

步骤4：对交叉后的抗体群实现自适应变异，群1抗体进行单点挪位变异，群2抗体则按前文所给变异规则进行模块内的变异。

2.3.3 种群更新与末尾淘汰机制

本文设置的知识记忆库中最佳亲和度值若连续U代未变将按照种群初始化方式重构下一代种群，否则先按亲和度降序排列交叉变异后的群体，再对末尾抗体实施克隆、变异，选出亲和度最大的抗体淘汰当前末尾抗体，亲和度相同则根据抗体编码和解码后作业的松弛时间选择相似度小的。

3 数值实验及分析

3.1 实验平台与实例参数

Lambrechts等［18］提取服从三角分布的离散数据为作业设定不稳定性成本权重，本文以相同方式使非虚拟作业权重服从参数为（0.01，0.06，0.10）的三角分布，结尾虚作业的权重从参数为（0.10，0.15，0.18）的三角分布中抽样1 000次取平均。每个作业仅有2类质量相关部件，初始衰退量lojq、cojq、sojq和gojq分别服从区间［0，1］、［0，1］、［0，3］和［0，10］内的均匀分布。质量相关部件的衰退服从gamma过程，其中形状参数和尺寸参数分别服从区间［0.001 35，0.001 56］和［0.018 70，0.033 60］内的均匀分布。调度算法中抗体规模为50，迭代20次，pc与pm算子中λ1=0.8，λ2=0.4，λ3=0.6，λ4=0.8。本文实验利用差值百分比G来衡量I-I-A相对其他B算法所得目标函数的改善程度。本文优化目标可能出现负数，按式（25）计算G，可直接通过G值分析出I-I-A相对不同算法的改善程度大小。G值为正数时表示I-I-A所得结果更优，G值越大表示I-I-A优化程度越明显。

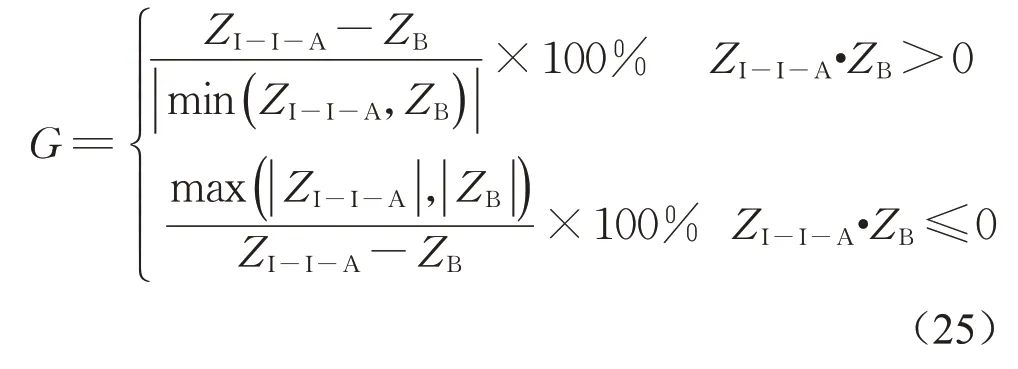
3.2 重调度算法性能对比

3.2.1 节选择了工程实践中常用的基于作业优先顺序的规则［19］AWA1和右移策略（RS）2种对比算法：①AWA1将作业按照在Fo中开始时间的先后顺序排列，所有修复作业安排至正常作业的后一位形成AWA1编码。②RS将修复作业安排在对应正常作业结束时刻开始执行，其他作业顺延到各自的紧前作业全部完成后开始执行［20］。考虑到I-I-A是启发式算法而AWA1与RS并非启发式算法，因此3.2.1进一步选取同样是启发式算法的遗传算法与I-I-A进行对比，验证I-I-A的有效性。需说明的是，3.2.1节单次预测下的每组对比实验仅对比单次预测-重调度后的装配计划的贡献值；而3.2.2节则模拟了装配现场时间驱动下按顺序进行的多次预测-重调度过程并对最终形成的总装配计划的贡献值进行后验对比。

3.2.1 单次预测下算法性能对比

实验在5种作业规模下进行，各规模下均取5个算例共进行5组实验，这5个算例分别有且仅有1个关键作业。每个算例下的一组实验需对关键作业激发预测机制并实现重调度的过程进行20次模拟，在保持预测部分一致的情况下对比运用I-I-A、AWA1和RS这3种重调度算法得到的调度计划在目标函数值上的表现。表1每组数据是该组20次模拟所得结果里与目标函数中位值所在次对应的数据信息。用G1和G2分别表示I-I-A与AWA1、RS的目标函数优化结果之间的差值百分比。表1中G1和G2列大部分为正数说明I-I-A结果基本都优于AWA1和RS，多数G2均值比G1均值大10%左右反映出I-I-A优于RS的程度大于AWA1。仅从目标函数优化结果可见I-I-A相比AWA1和RS有显著的改善效果，但I-IA的运算时间远远大于AWA1和RS，主要因为本文的I-I-A需迭代寻优而AWA1和RS并不存在迭代搜索过程。

考虑到本文I-I-A属于启发式算法，遗传算法（GA）作为经典启发式算法其解决调度问题的适用性和有效性已被大量文献研究验证，为进一步验证I-I-A的算法性能，将其与GA进行对比。GA在种群规模和迭代总数上与I-I-A保持一致，但交叉和变异采用固定概率0.8和0.7，初始种群仅采用一种随机生成方式。该对比实验中各算例都确定了10个激发预测机制的关键作业，每个算例进行3次实验，每次实验这10个关键作业在保持前端一致而后端分别采用I-I-A和GA可得到10个调度结果和对应的目标函数值，I-I-A优化得到的目标函数值与GA优化得到的目标函数值之间的差值百分比用G表示，表2汇总了每次实验10个实验结果的最大、最小、平均G和2种算法的运行时间。

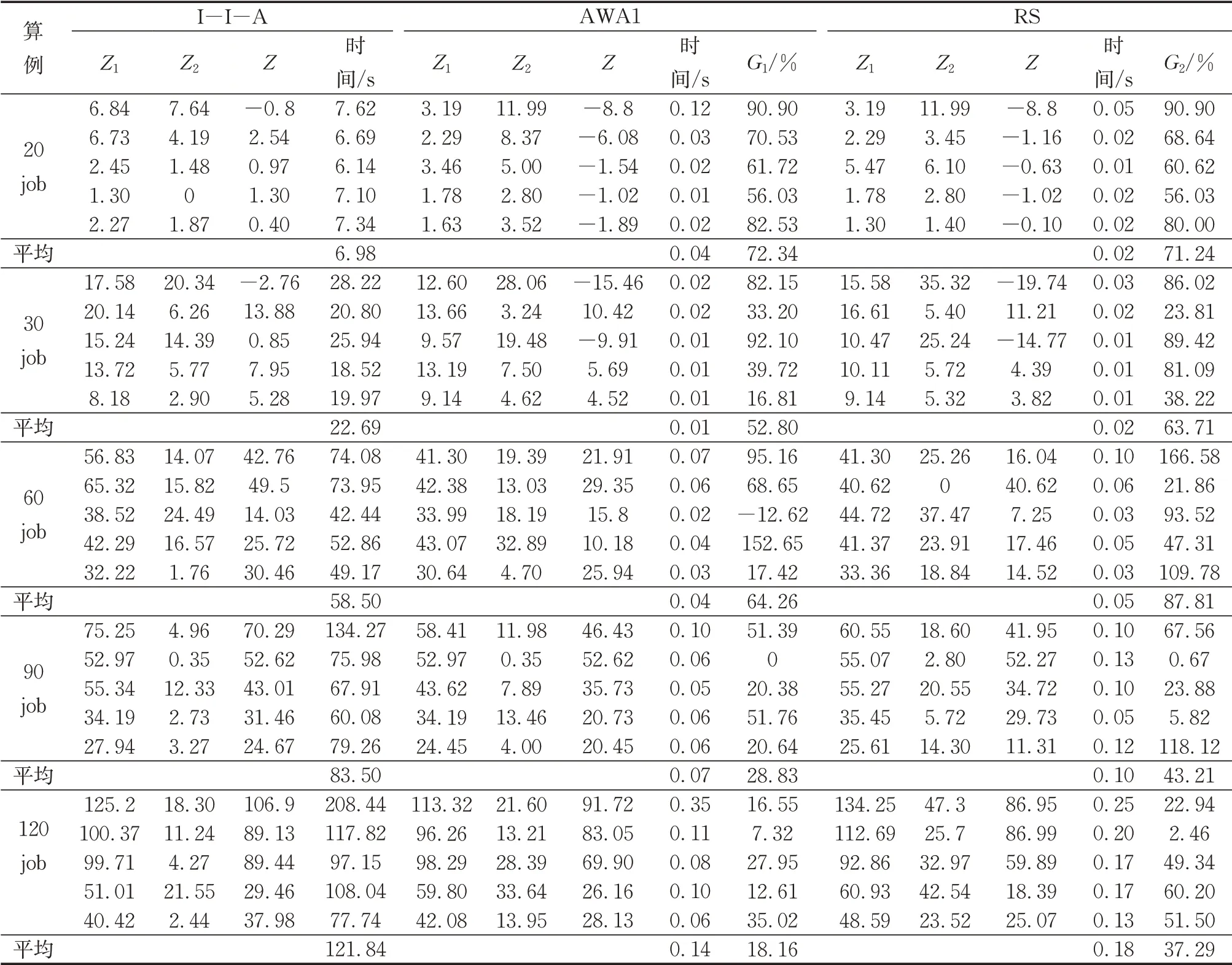
表1 单次预测下I-I-A与AWA1以及RS对比结果Tab.1 Comparison of results of I-I-A,AWA1,and RS in single prediction

表2各算例实验组下的平均G基本都在12%以上，60job时G的均值达到了29.61%，可见I-I-A的优化结果明显好于GA，并且I-I-A在运算时间上仍略优于GA特别是在作业规模较大的算例中平均节约时间在6s左右。I-I-A在设置了知识记忆库和末尾淘汰机制的情况下运算效率仍高于GA，侧面反映出I-I-A中已改进部分的高效性。

3.2.2 多次预测下调度计划后验对比实验

飞机装配项目中装配作业多且装配时间长，通常存在多个关键作业也需进行多次预测和装配计划调整的情况。图3给出了3次执行预测-重调度（采用AWA1规则）后所有作业实际的总调度计划。图中第3次预测-重调度后形成的总调度计划是第1、2、3次预测-重调度过程累积而成的总调度计划，若当前工位进入一个完全相同的新项目，该总调度计划对制定新项目的装配计划具有重要参考价值。本部分实验模拟多次预测-重调度过程并对比不同重调度算法形成的实际总调度计划在目标函数上的表现。该实验将工程中常用的AWA1规则改进成AWA2（即作业按Fo中开始时间的顺序排列），若同时开始则w j+W j越大调度优先级越高，所有修复作业插入至对应正常作业的后一位形成AWA2重调度编码。

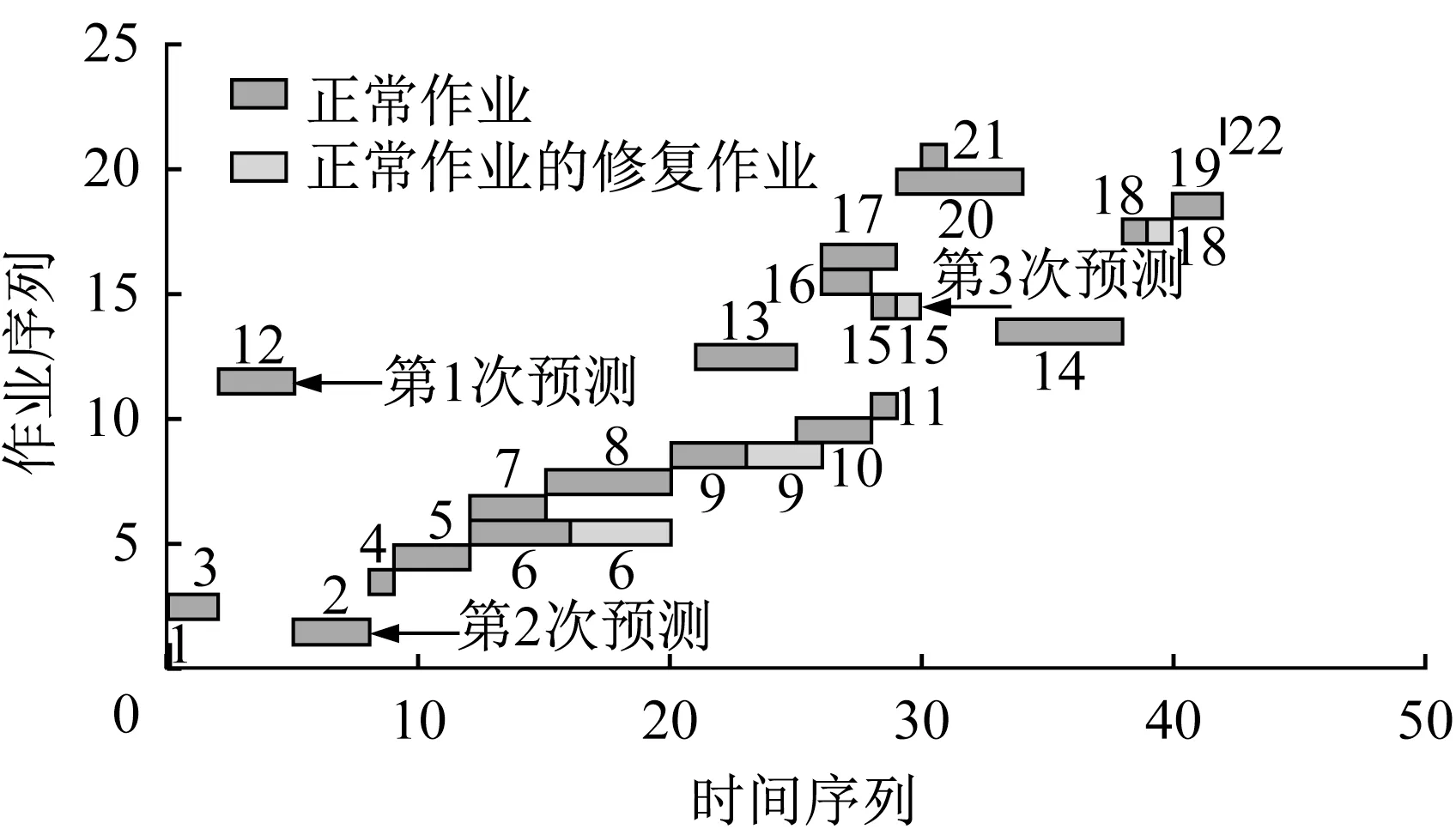
图3 多次预测后实际调度计划示意Fig.3 Actual scheduling plan after multiple predic⁃tions

AWA1、AWA2与I-I-A的对比实验在20job的算例下进行，列表［1，3，12，2，4，5，7，9，8，16，15，10，11］用于挑选激发预测机制的作业，激发作业规模介于区间［2，10］内，各规模下从列表中随机选择30组不重复的作业并进行30组预测-重调度仿真模拟。该实验采用G3和G4分别表示I-I-A与AWA1、AWA2得到的总调度计划在目标函数结果上的差值百分比。

不同激发作业规模下30组对比实验的G3和G4分布分别如图4深色与浅色箱形图所示，图中十字形点是30组数据里太大或者太小的数据视为异常值的点。与图4相关的数据见表3。图4不同规模下G3和G4的分布多为正数且形状相似，这说明I-I-A的优化能力强于AWA1和AWA2并且I-I-A优于AWA1和AWA2的程度基本相同。

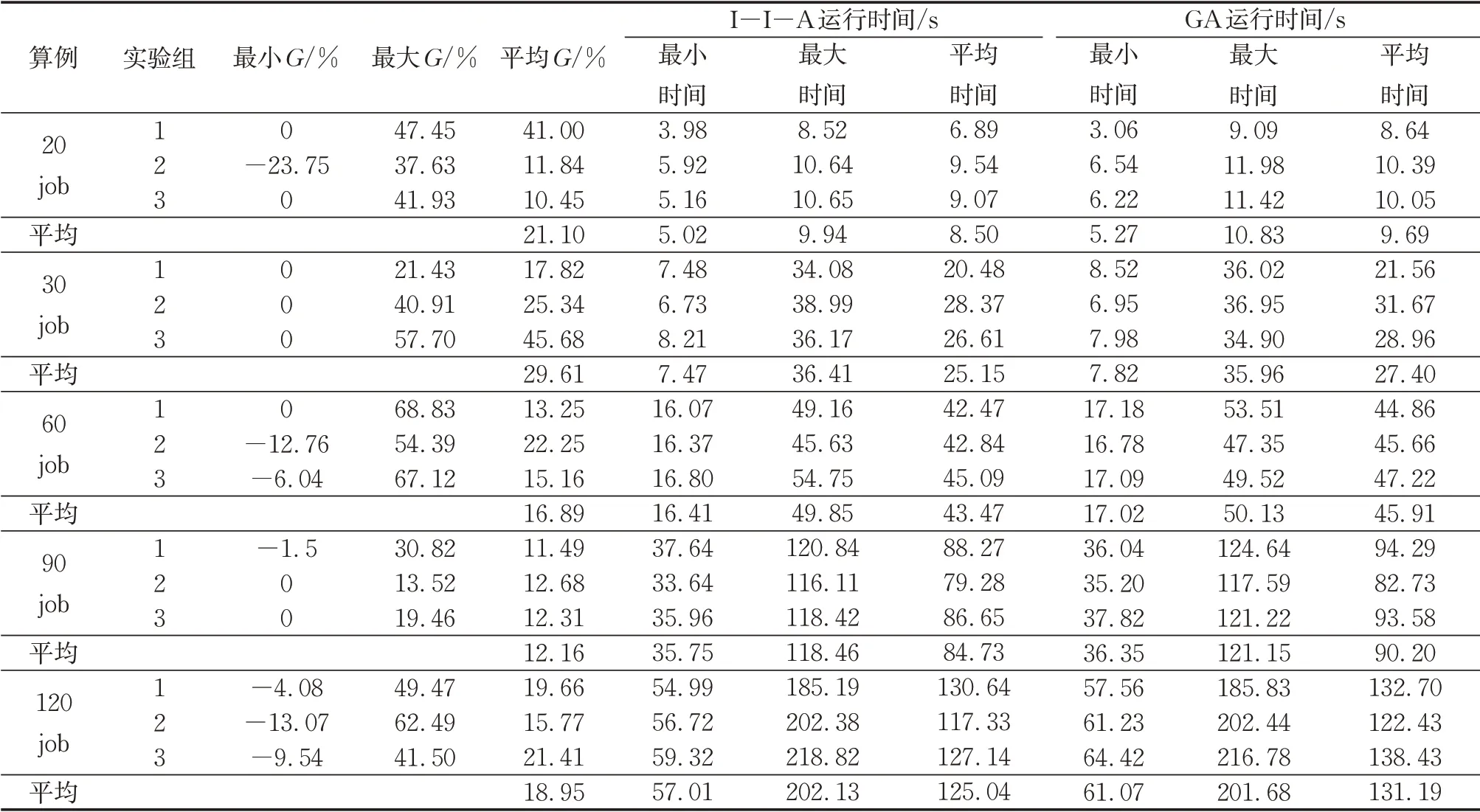
表2 单次预测下I-I-A与GA对比结果Tab.2 Comparison of results of I-I-A and GA in single prediction

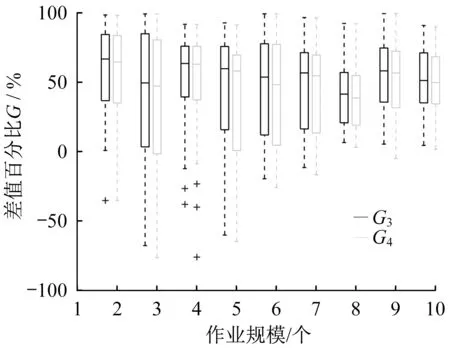
图4 不同激发作业规模下的G值分布箱形图Fig.4 Box-plot of G distributions in different scales of trigger jobs

表3中较小四分位值、中位值和较大四分位值是将各激发规模下的30组G3（G4）升序排列后第25%，第50%和第75%个位置的G3（G4）值，分别对应图4矩形盒下、中、上3条线所示G值。表3较小四分位值对应列的G值大部分都是正数说明多数规模下的30组实验结果中I-I-A至少有75%的结果优于AWA1或AWA2且30组G值中有75%的数据大于表中所给值，但激发作业规模为3和5的数据中也分别出现G4的较小四分位值是-2.54%和-0.254%的情况，说明这2种规模下的30组实验中至少有25%的组数I-I-A的结果不如AWA2好，一定程度上反映出经改进的AWA2规则在某些情况下性能优于I-I-A。进一步分析表3，从G中位值以及较大四分位值来看G3和G4均未再出现负数并且G3和G4均值基本都大于40%，说明I-I-A不仅能在单次预测-重调度下生成贡献值较大的重调度计划，多次预测-重调度后形成的总调度计划相比AWA1和AWA2而言依然具有更高的贡献值，可为新进入当前工位的装配项目提供更合理的装配计划模板。

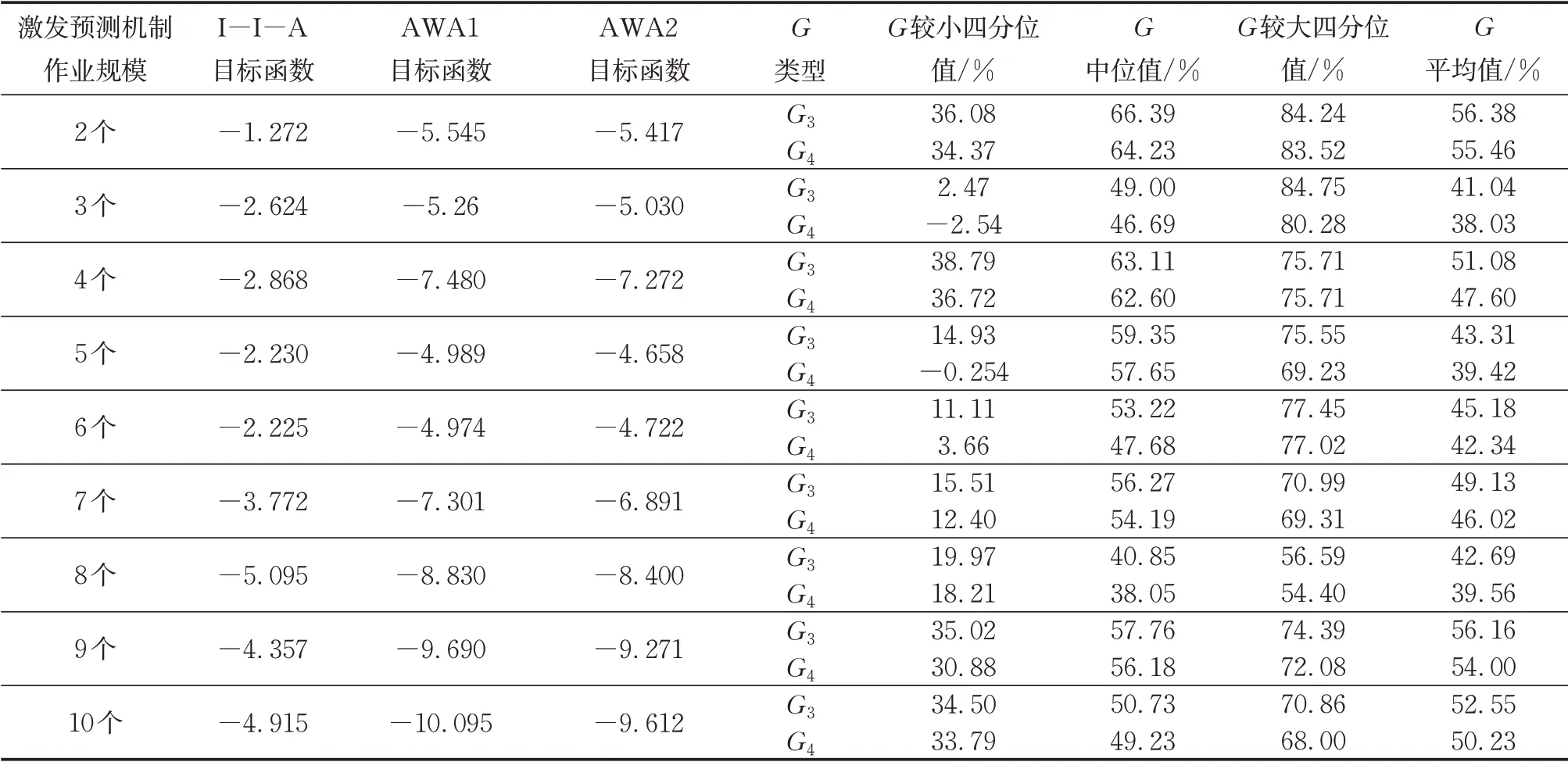
表3 不同激发作业规模下目标函数值和G值表现情况Tab.3 Performance of objective and G values in different scales of trigger jobs

3.3 整体框架性能分析

3.2 节仅对比后端重调度算法并验证了I-I-A的效果和效率，不能体现本文所提预测-重调度框架的优势，本节将该框架与文献中经典的前摄调度框架以及纯反应型重调度框架进行对比，对比实验中采用了前摄-右移框架和反应-右移框架。前摄-右移框架在初始调度计划中事先插入部分缓冲时间用以应对可能的修复干扰，当有修复作业插入时采用右移策略更新调度计划；反应-右移框架不插入缓冲时间，仅在有修复作业加入时才采用右移策略更新调度计划；本文框架在计划执行过程中主动预测并基于预测结果预调度一部分修复作业从而减少未来可能的修复干扰。本文框架前端SVR预测模型的平均准确率接近81%，各算例实验通过抽样仿真模拟不同框架下计划执行的完整过程，修复场景根据作业的合格概率随机抽样得到，各算例下的5组实验抽样场景数均为50。需说明的是前摄-右移框架和反应-右移框架除初始计划不同，其他无区别，使用相同的抽样场景。本文框架、前摄-右移框架、反应-右移框架在50个仿真场景下得到的调度计划平均周期时间见表4中的周期1、周期2和周期3，仿真中实际右移次数的平均值见最后3列数据。

表4部分算例本文框架相比前摄-右移框架在调度计划平均周期上缩短了10个单位左右，主要原因是本文框架不在初始计划内插入缓冲而仅基于预测结果预调度部分修复作业因此降低了缓冲时间的冗余程度，实验结果也反映出前摄-右移框架事先插入的缓冲时间针对性弱预防作用较小；本文框架与反应-右移框架在调度计划平均周期上非常接近但也有近4个单位时间的减少并且平均右移数目也少了近4次，这意味着本文框架减少了预期外质量修复作业加入导致的事后型计划调整次数，进一步体现出本文框架通过事前预测能准确预调度出一部分修复作业便于在修复需求产生时直接按预调度计划执行。但是，本文框架也需付出预测-重调度的运算时间代价，由于算例中调度作业的时间单位未明确给出，因此无法与算法时间单位（s）统一，更难将包括预测部分在内的整体算法运行时间一同纳入调度仿真中以给出包含运算时间的最接近应用实际的调度计划周期，但是实际工程中可根据事前预测-重调度与事后重调度消耗时间和成本的具体情况选择最合适的框架。

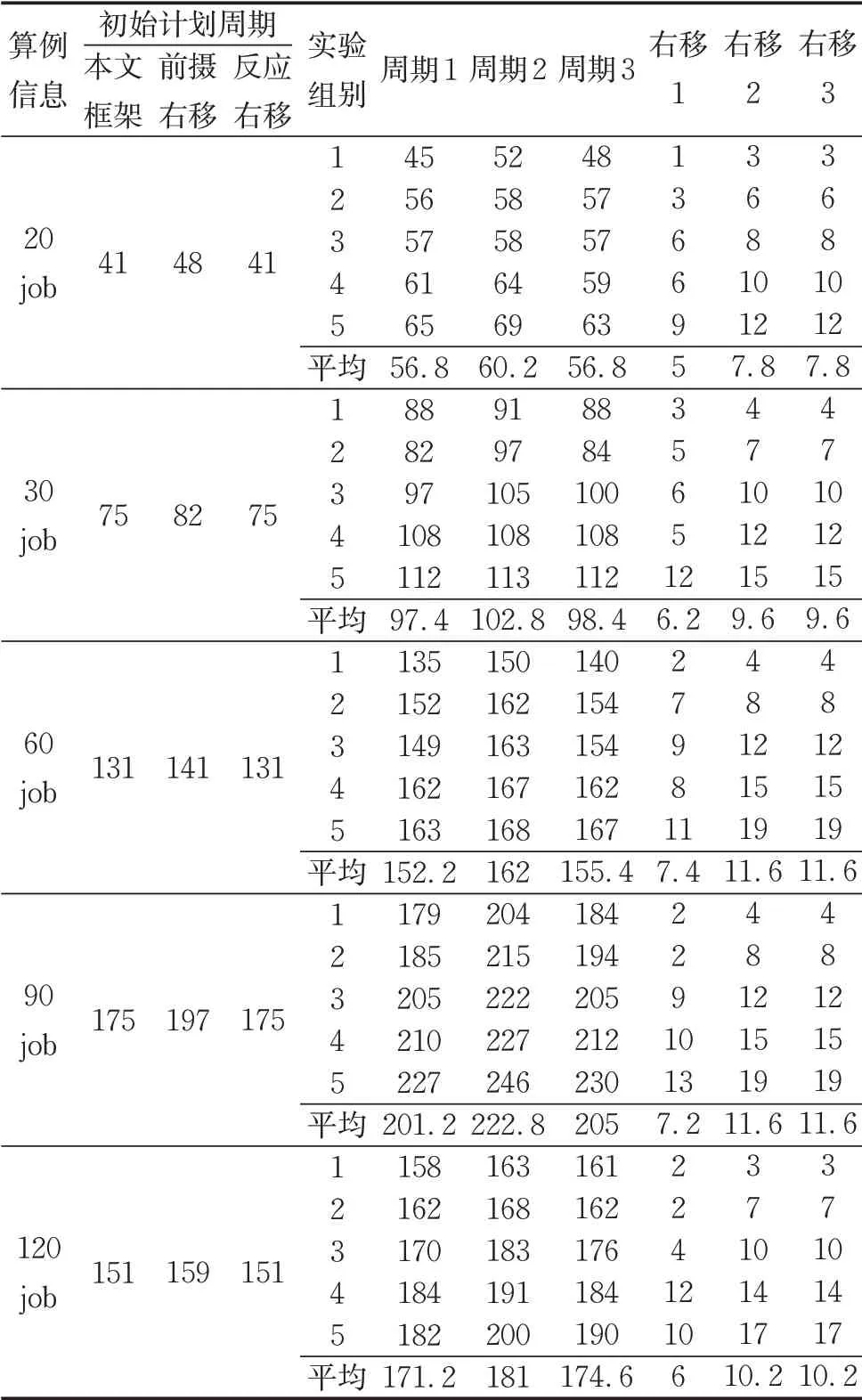
表4 各算例下不同框架仿真结果Tab.4 Simulation results of different frameworks in each case

4 结语

（1）以飞机移动装配线为背景，针对质量修复作业的加入干扰调度计划的问题提出了基于预测机制的装配作业重调度框架，框架前端训练了质量预测模型，后端建立了作业重调度模型。

（2）提出了重调度算法I-I-A并通过不同的对比实验验证有效性。总体看，I-I-A在优化效果和效率上均好于GA；相比AWA1和RS，I-I-A虽能得到更佳的优化结果但在简便程度和算法运行时间上的劣势也较明显。

（3）相比现有文献中利用公式推导实现前摄调度，该框架可掌握更准确的实际装配信息进而得到更准确的预测结果，有利于降低计划中所插缓冲时间或资源的冗余度。此外，相比起反应型调度方式，本文框架更利于保持项目执行过程的稳定性。

（4）后续进一步优化前端预测模型并构建前后端的集成优化模型。