基于弱耦合求解方法的排水管网底泥输运模拟

金 溪，王 芳，张翔凌

（1.武汉理工大学土木工程与建筑学院，湖北武汉430070；2.武汉市规划研究院，湖北武汉430014）

排水管网底泥的淤积和冲刷会造成许多问题。随着城市化的发展这些问题表现得越来越突出，尤其是在使用合流制管网的地区这些问题的影响尤其严重。近几年来排水系统底泥输运造成的环境问题成为了相关领域的研究热点［1-2］。

目前，相当多的研究聚焦于将一维或二维水力模型与底泥输运模型进行耦合，实现对于底泥沉积及冲刷过程的模拟［3-4］。但是研究的内容集中于个别管段在单场降雨中导致的污染物释放问题，无法在管网的规模上进行考虑底泥输运问题的水力和水质模拟，并且研究内容缺少对于底泥沉积过程的考虑，因此无法在长周期上对底泥淤积量的变化进行预测。Seco等［5］提出了一种基于SWMM（storm water management model）与底泥污染物释放模型的模拟方法，可以在管网规模上进行考虑底泥污染物冲刷的水质模拟，但是模拟过程中SWMM与底泥污染物释放模型是完全分开计算的，因此并不是一种耦合模拟过程。

为了实现考虑底泥输运问题的排水管网水力、水质模拟，提出一种基于SWMM及底泥输运模型（sediment transport model，STM）耦合模拟的计算方法，在考虑底泥淤积和冲刷的情况下进行水力、水质模拟。

1 控制方程

在管渠底泥输运模型中，其控制方程常用Saint-Venant-Exner（SWExner）方 程 组 进 行 描 述。SWExner方程组的形式如下所示。连续性方程为

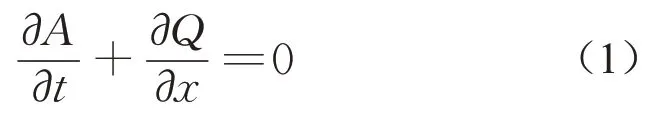
动量方程为

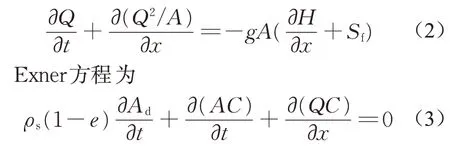
其中：x为流行距离，m；t为时间，s；A为管渠过流断面面积，m2；Q为流量，m3·s-1；H为水头，m；Sf为水力坡度；g为重力加速度，m·s-2；ρs为底泥干密度，kg·m-3；e为底泥空隙率；C为水中悬移质浓度，kg·m-3；Ad为管渠底部沉积物横断面积，m2。

在求解SWExner方程组时可以利用经典的计算流体力学方法以及Exner方程求解方法对其进行耦合求解。许多研究者利用该思路对SWExner方程组的求解进行了研究，并验证了其可行性［6-9］。

SWExner方程组的求解方法可以分为两大类：完全耦合求解方法（1-step approach）以及弱耦合求解方法（weak coupling approach）。对于完全耦合求解方法，在每一个时间步长的求解过程中，需要考虑底泥输运对于管道流动的影响，并且管道的流动按照非恒定流进行考虑，因此SWExner方程组中的方程需要同时求解。而在弱耦合求解方法中，每一个时间步长中，管段的流动假定为恒定流动，并且假定底泥输运对于水在管道中的流动没有影响。通过上述假设，在弱耦合求解方法中可以先进行Saint-Venant方程组的求解，再将Saint-Venant方程组的水力计算结果作为已知条件代入Exner方程进行求解。多名研究者对完全耦合求解及弱耦合求解方法进行了综合比较［10-11］，总体上来说完全耦合求解方法适用的场合更广泛，尤其在流量及悬移质浓度剧烈变化导致底泥形变或运动速度较快的场景下完全耦合求解方法可以给出更好的模拟效果，但是该方法也具有计算量大、耦合机制复杂的缺点。相对应的，弱耦合求解方法只能用于底泥形变或运动速度相对于水流速度较低的情境下，否则其前提条件将无法满足，影响模拟效果。但是弱耦合求解方法具有求解简单、对Exner方程的形式适应性更强等特点。Cunge等［12］认为，对于大多数底泥输运问题，底泥的运动速度一般远低于水流的速度，因此弱耦合求解方法可以应对绝大多数底泥输运问题的模拟场景。多名研究学者将弱耦合求解方法用于排水管段底泥输运问题的求解，取得了较好的效果。验证了弱耦合求解方法在排水管道场景应用的可行性［13-14］。通过上述比较以及对排水系统中底泥输运特点的考虑，采用弱耦合求解方法对SWExner方程组进行求解。

在耦合求解的过程中，SWMM5［15］被用来求解SWExner方程组中的Saint-Venant方程组部分。在SWMM5的水力、水质模型求解过程中，管段被看作最基本的计算单元，忽略了各个变量数值沿管长的变化。因此当Exner方程与SWMM5进行耦合计算时，其方程中的（∂（QC））/∂x部分被忽略掉，从而简化为方程（4）所示的形式：

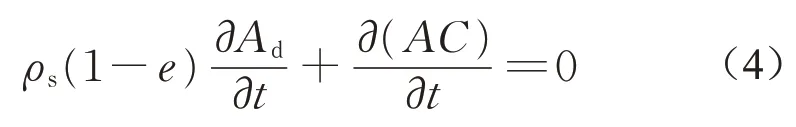
求解Exner方程的目的是获得Ad与C的值。由于该方程中具有2个未知量，因此需要补充一个方程使其封闭。这里补充如公式（5）所示的河床形变方程：

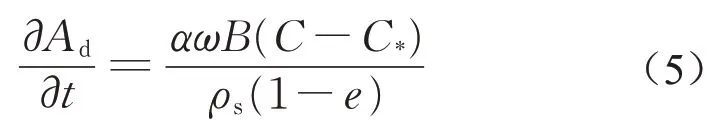
其中：α为恢复饱和系数，表示在冲刷（或者沉积）过程中实际冲刷（或沉积）的底泥质量占潜在的可能被冲刷（或沉积）的底泥质量的比例；ω为底泥颗粒的沉降速率，m·s-1，沉降速率与底泥颗粒粒径ds（mm）具有很强的相关性，本研究中ω与ds之间的数值关系采用Chen［16］总结的方程进行描述；B为底泥横断面表层宽度，m；C*为水流的携沙能力，kg·m-3，这里采用张丽春等［17］中总结的携沙能力计算公式进行描述：

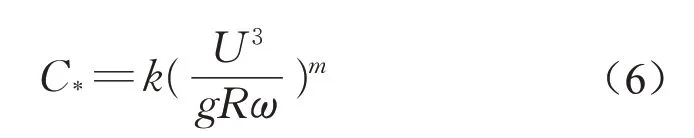
其中：U为管渠过流断面平均流速，m·s-1；R为管渠过流断面水力半径，m；k、m为经验参数，其取值与U3/（gRω）的数值有关，这里采用张小峰等［18］总结的k、m与U3/（gRω）的数值关系进行k、m值的计算。

2 求解方法

在耦合求解过程中SWMM5负责计算水力、水质变量数值，包括Q、H、U、C，然后利用上述变量值代入Exner方程获得Ad与C的值。在上述过程中C被更新了2次，SWMM5计算获得的C为不考虑底泥颗粒沉积和冲刷因素情况下获得的底泥颗粒在水中的浓度。而Exner方程的求解则是在考虑底泥输运的情况下对底泥颗粒的浓度以及管底底泥的体积进行更新。通过上述耦合求解方法可以实现在考虑底泥输运情况下的管网水力、水质以及管底底泥淤积情况的模拟。该求解过程可以被描述为下述步骤：

（1）SWMM5演进一个时间步长，获得Q、H、U、C数值。

（2）Exner方程求解的准备。获得ω、R、B的数值，根据U3/（gRω）的数值获得k、m数值，最后计算C*的数值。

（3）Exner方程求解。联合求解方程（4）、（5）获得Ad与C的值。

（4）Exner方程求解结果的校验与修正。Ad与C的计算结果没有考虑耦合求解的数值稳定性，因此需要对结果进行校验与修正，其方法详见2.2节。

（5）管段水力横断面的更新。根据Ad的数值对管段的水力横断面进行更新。返回步骤（1）或者结束模拟。

在上述求解过程中水中悬移质浓度C可以利用SWMM5模型中定义的某一种污染物来代表，例如定义TSS（total suspended solid）代表水中悬移质浓度。

2.1 管段水力横断面的更新

在耦合求解过程的第（5）步需要对管渠的横断面依据Ad进行更新，但是在SWMM5中没有断面类型可以在模拟过程中进行调整，因此需要对SWMM5的代码进行适当修改，增加一种可以在模拟过程中更新几何尺寸的断面类型。以SWMM5中的可淤积圆管（filled circular）断面类型为基础创建一种可以在模拟过程中改变断面几何参数的断面类型。可淤积圆管中的淤积深度（filled depth）属性被用来描述底泥淤积深度，并且该属性需要在每一个时间步长中根据Ad的计算结果进行更新，更新方法如下所示：

（1）根据Ad计算结果更新淤积深度。

（2）根据淤积深度更新淤积表面的宽度以及满流条件下的水力半径。

（3）根据淤积深度更新管段进出口的偏移高度。

2.2 耦合求解过程中的数值稳定性

耦合求解过程中需要将时间离散为较短的时间步长，而时间步长长度的确定对于求解过程的稳定性具有非常重要的影响。通过上述耦合过程的描述可以看出，SWMM5模型为耦合求解过程的整体框架，Exner方程的求解被嵌入在SWMM5的步长中，因此耦合的时间步长长度是由SWMM5的时间步长确定机制控制的。SWMM5的时间步长是利用Courant-Friedrichs-Lewy（CFL）原则确定的，CFL原则确定的时间步长仅能满足Saint-Venant方程组求解对数值稳定性的要求，而无法保证Exner方程求解的数值稳定性。

Exner方程求解出现数值不稳定的情况主要是因为在求解过程中没有考虑水流携沙能力对于沉积物浓度变化范围的限制。实际上在一个时间步长内如果沉积物的浓度（C）达到了水流的携沙能力确定的浓度（C*）后，沉积物的沉积与冲刷会达到一个平衡状态，从而使得沉积物浓度停留在当前时间步长内水流携沙能力确定的沉积物浓度数值。因此在Exner方程求解过程中，在获得了C与Ad的计算结果以后需要利用C*进行校验与修正。校验与修正的过程为：

（1）首先通过比较沉积物浓度初始值（C0）与携沙能力（C*）判断当前时间步长内是冲刷过程还是沉积过程。

（2）如果为沉积过程，比较沉积物浓度计算结果C与C*的数值，如果C＜C*则赋值C=C*，并利用公式（4）重新计算Ad；如果为冲刷过程，比较C与C*的数值，如果C＞C*则赋值C=C*，并利用公式（4）重新计算Ad。

上述修正过程的流程可由图1表示。

通过上述修正方法可以在不改变SWMM5时间步长确定机制的条件下，实现耦合过程的数值稳定性。但是这种方法在处理高浓度、高沉降性（如粘滞性性小、粒径较大）的沉积物颗粒时，仍然可能出现相邻时间步长C、Ad计算结果差异较大的情况，虽然不会出现数值震荡的情况，但是可能增加模拟过程的连续性误差。这种情况下可以通过缩小SWMM5的时间步长（routing step）来减小连续性误差。

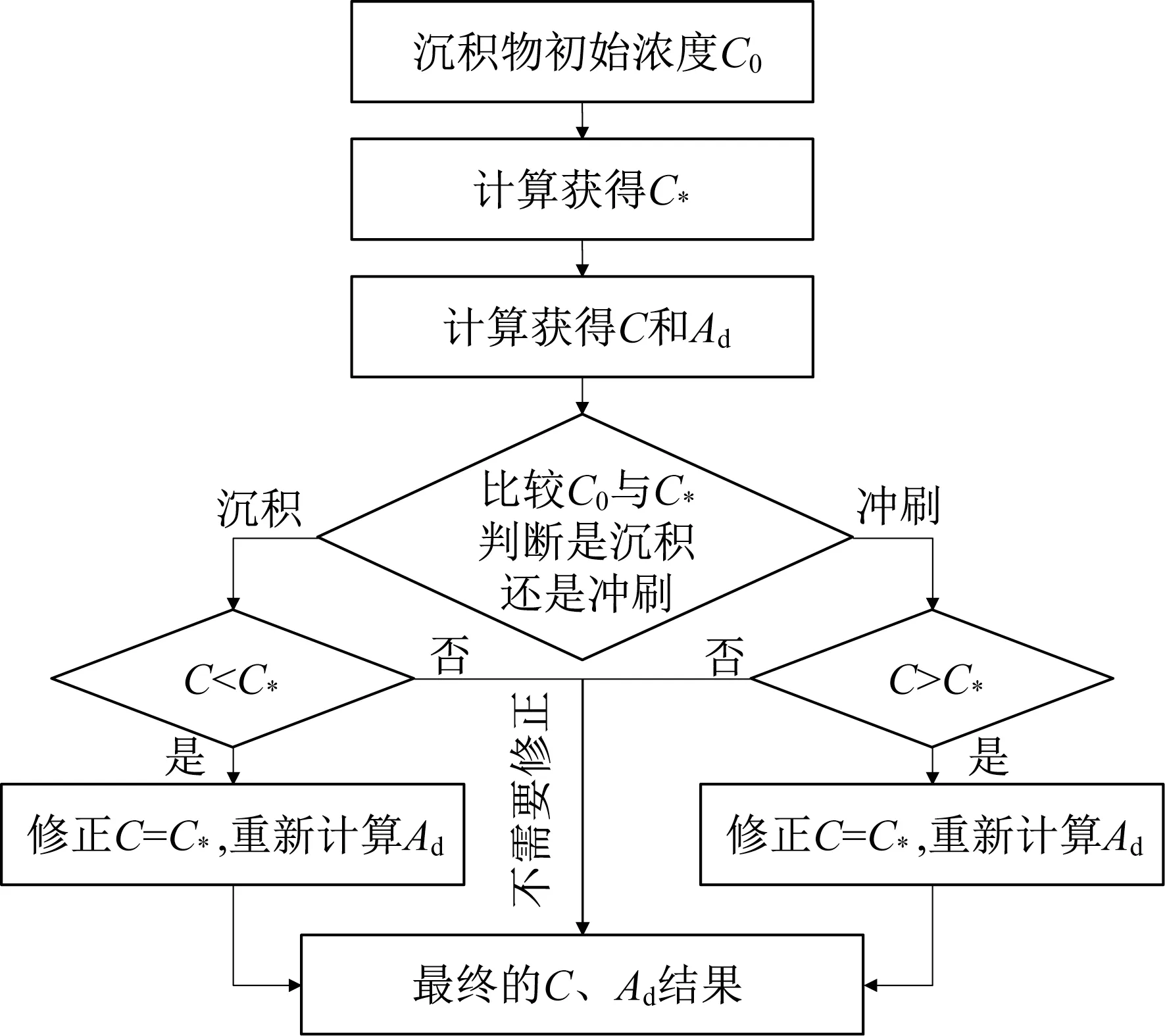
图1 沉积物浓度计算结果验证与修正流程Fig.1 Flowchart of validation and correction sedi⁃ment mass concentration

3 案例研究

将上述耦合计算方法应用2个不同的案例模型中。模型1为一个简单的虚拟排水管网，其管网结构如图2所示，参数见表1。

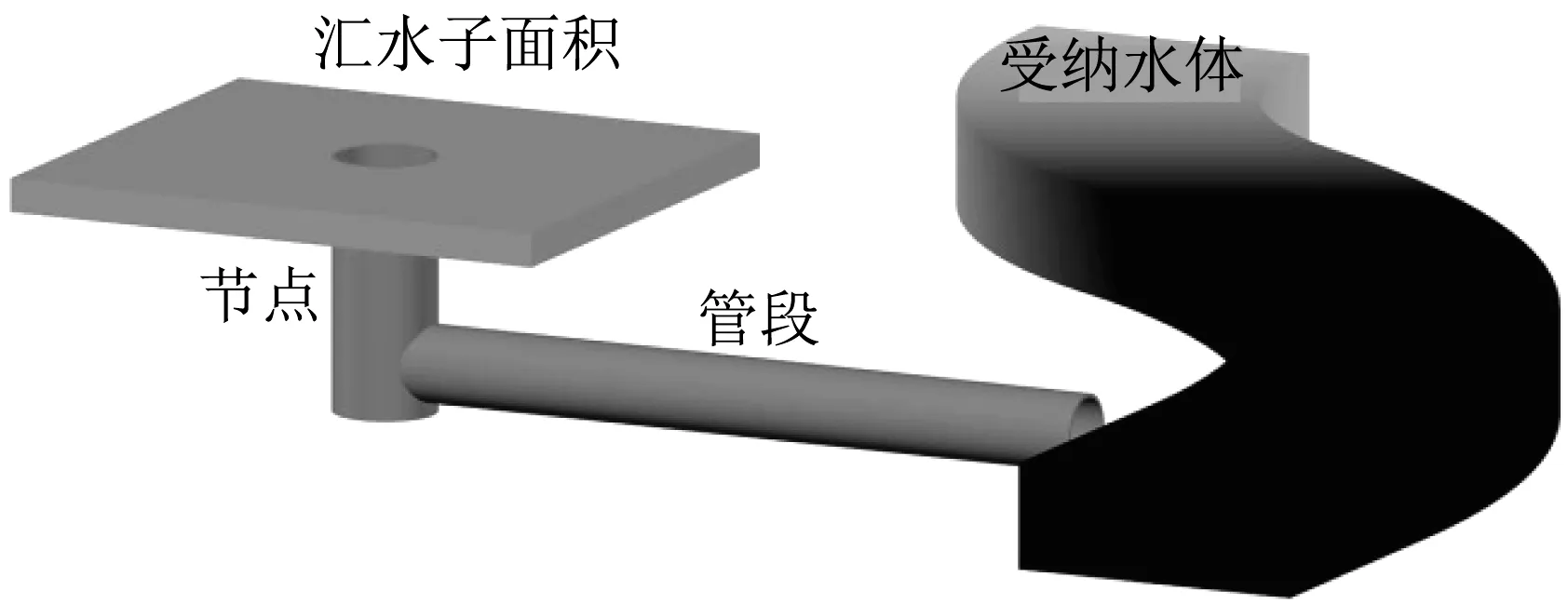
图2 案例1管网结构Fig.2 Sewer network of case1

管网中各图元的属性如表1所示。该案例的作用是对于耦合算法的计算过程的数值稳定性及连续性误差问题进行分析。

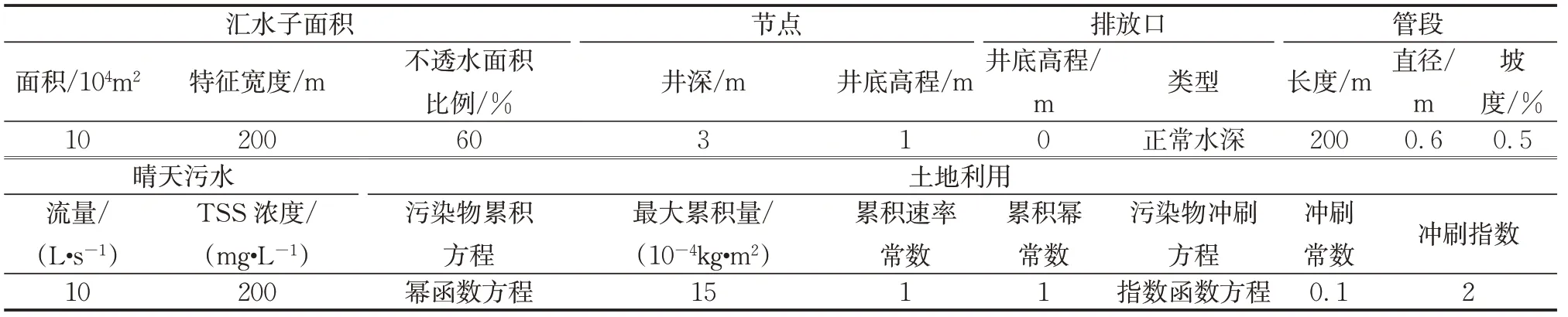
表1 案例1管网模型基本参数值Tab.1 Parametersof features in sewer network of case1

案例2为巢湖市某区域排水管网系统，利用4场降雨的监测数据对耦合方法的计算结果与SWMM5模型的计算结果进行对比，以评估耦合模型的模拟效果。案例2研究区域的管网图如图3所示。监测降雨分别为当地时间2011-06-24，2011-07-12，2011-07-17以及2011-07-26的降雨。案例2管网模型的基本参数值如表2所示。

表2 案例2管网模型基本参数值Tab.2 Parameters of features in combined sewer network of case 2

研究区域内管网在4场降雨过程中的水力模拟的准确性是水质模拟准确性的基础，因此必须首先对模型进行水力模拟校核，通过调整汇水子面积相关属性的参数使模型的模拟结果与监测流量数据达到较好的模拟效果。水力校核的结果如图4所示。

4 结果与讨论

4.1 案例1模拟结果与分析

为了模拟管网底泥在长周期运行中淤积深度的变化，对案例1模型利用弱耦合求解方法进行了4年的长周期模拟，其中降雨数据的时间步长为1h，管段底泥初始淤积深度为0.1m。管段底泥淤积深度以及水中TSS浓度的SWMM5模拟结果以及弱耦合求解方法模拟结果的对比如图5所示。

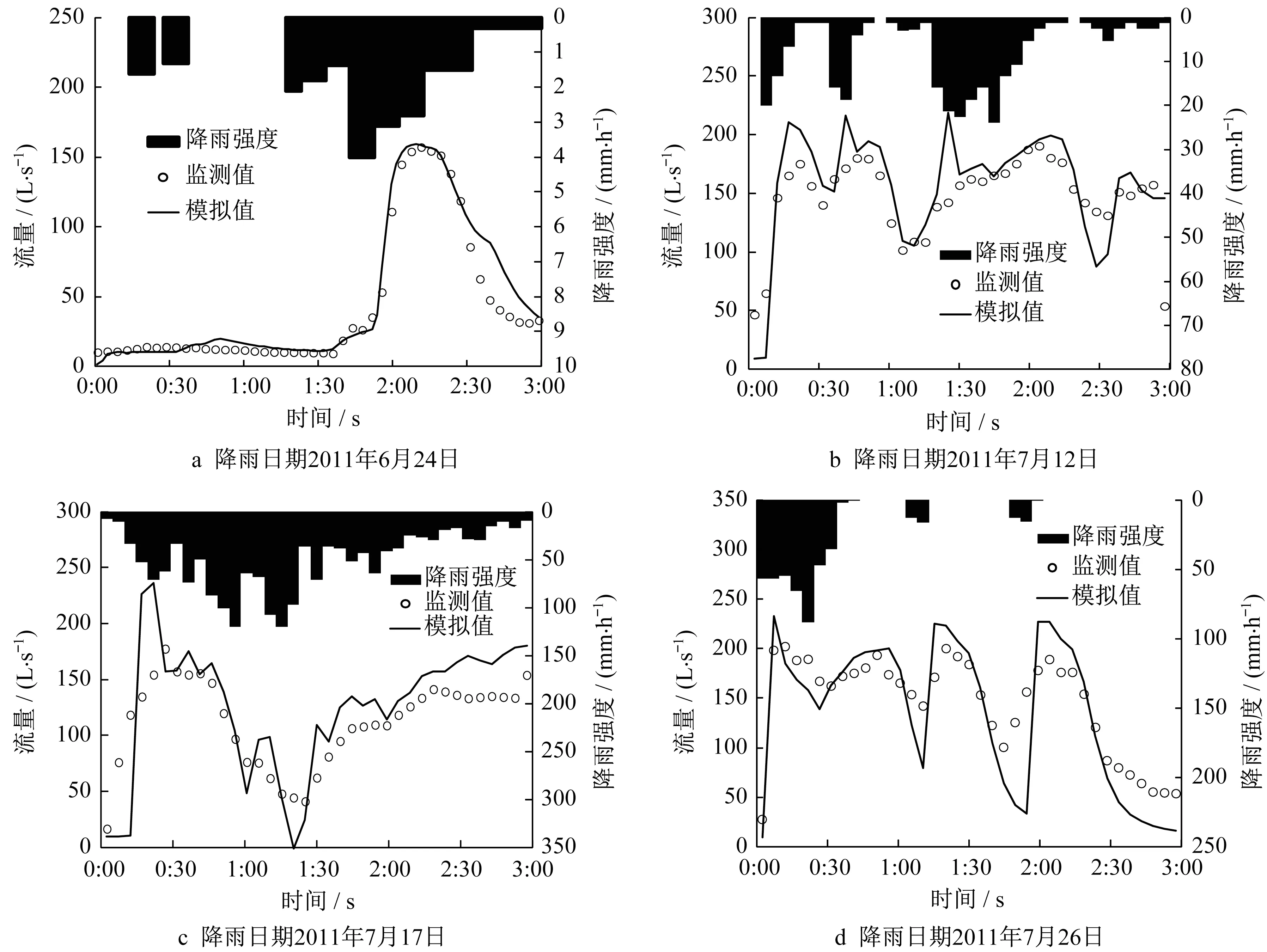
图4 研究区域管网水力模拟校核结果Fig.4 Calibrated result of SWMMhydraulic simulation of case 2

通过图5 a、5b可以看出，通过耦合模拟方法可以模拟出管底淤积以及管网水质情况随降雨而产生的变化，在降雨密集的时间段，由于管内流量的增加造成底泥冲刷，从而降低了管底的淤积深度，同时管道水流的TSS浓度显著增高。而在降雨较少的时期，晴天流量中的TSS会在管底造成淤积，出现管底淤积深度增加而管道内水流TSS浓度降低的情况。相对应的，由于SWMM5模拟中没有考虑管底淤积物的冲刷和淤积对于淤积深度和污染物浓度的影响，其管道淤积情况不会随着时间发生变化，并且水中TSS的浓度没有考虑雨天底泥冲刷的影响，因此浓度值普遍偏低。

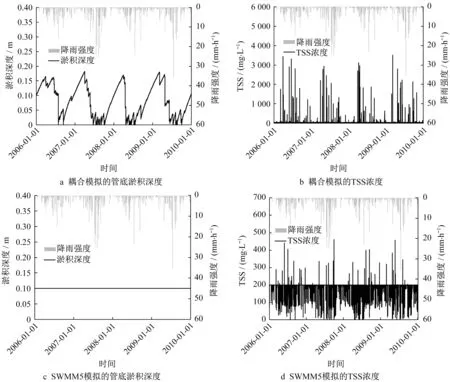
图5 案例1SWMM5模拟结果与耦合模拟结果对比Fig.5 Comparison of simulation results with and without coupling process of case 1

在耦合求解过程中数值稳定性以及连续性误差的大小是衡量求解方法质量的重要指标。在求解过程中，输入的TSS质量（Minlet）、排出的TSS质量（Moutlet）以及由于冲刷或淤积导致的水中TSS质量变化（Mdf）之间需要满足质量守恒原则，即满足关系式：Minlet=Moutlet+Mdf，其中Mdf在冲刷情况下取负值，在淤积情况下取正值。在理想情况下这个关系式应该被严格遵守，但是由于采用时间离散的方式进行求解不可避免会产生误差，如果误差较大则说明求解方法存在问题或者某些参数值设置不合理。图6显示了案例1的4年模拟过程中某个降雨冲刷时段（6h）的连续性误差时间过程线。

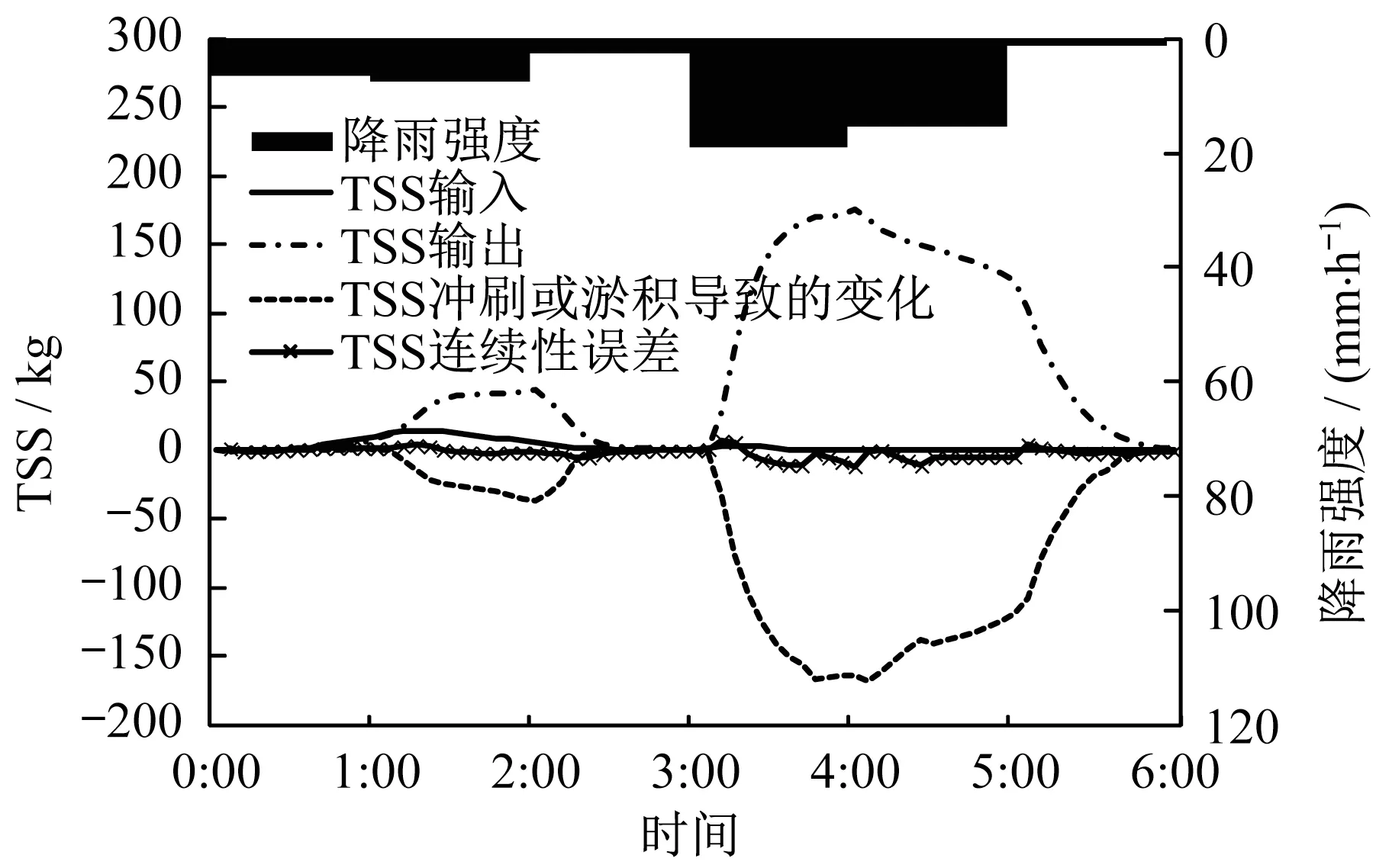
图6 案例1沉积物连续性误差时间过程线Fig.6 Time evolution of sediment mass error of case1

从图6可以看出，在整个冲刷过程中连续性误差的值在很低的范围内波动。误差的量化指标可以通过相对误差（E）来表示，相对误差的计算公式如公式（7）所示：

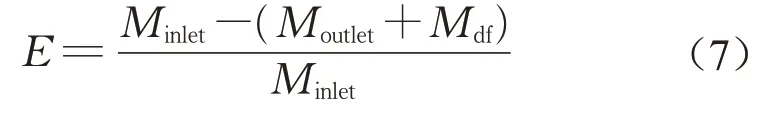
在所截取的6h时间段内，TSS连续性误差的值为-3.18%，在整个4年的模拟时段中TSS的连续性误差值1.83%。上述结果说明弱耦合求解方法在进行排水管网底泥输运模拟中可以保持数值的稳定性及较低的连续性误差。

为了验证耦合求解过程在污染物变化剧烈的条件下是否仍然能保持计算的稳定性及低连续性误差，将案例1中晴天流量TSS浓度提高至5 000mg·L-1，同时为了比较不同恢复饱和系数（α）及不同时间步长（Δt）对于数值稳定性及连续性误差的影响，对于沉降颗粒的恢复饱和系数及时间步长取不同的数值进行多次模拟。恢复饱和系数取值为0.010、0.025、0.050、0.10、0.250、0.500、1.000。时间步长取值为0.5s、1s、2s、5s、10s、30s、60s。α与Δt共有49种组合，对每种参数组合逐一进行模拟，图7展示了所有参数组合对应的模拟结果中TSS连续性误差以及流量连续性误差。

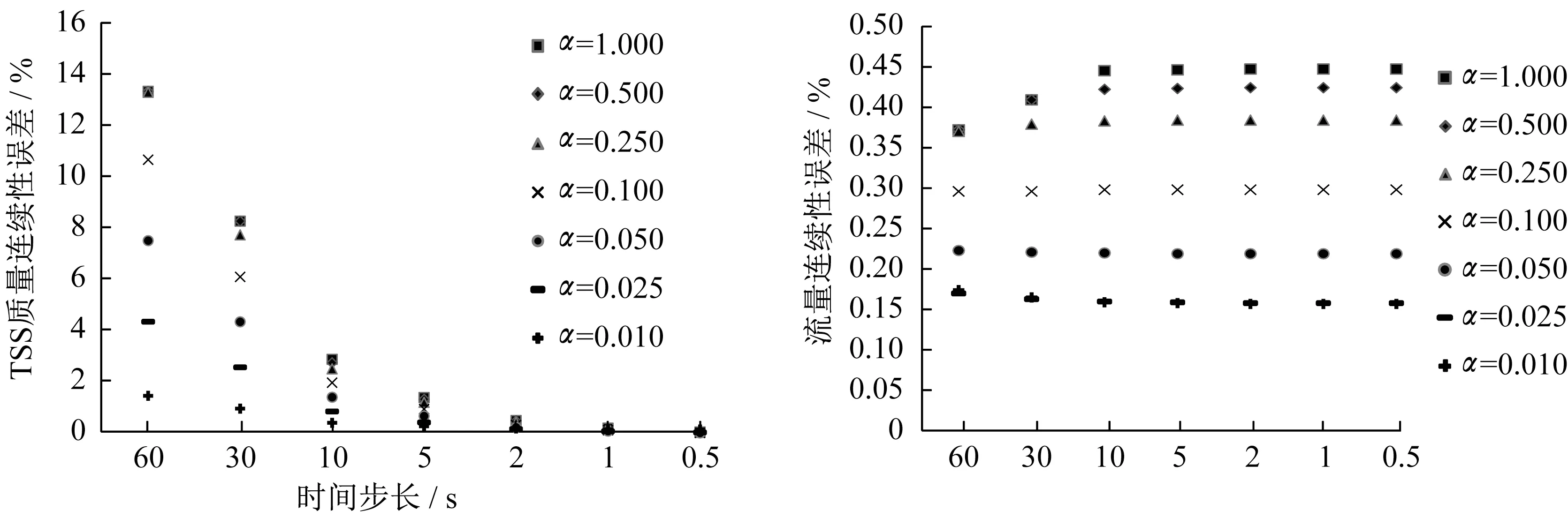
图7 案例1不同α、Δt参数组合情况下的TSS及流量连续性误差Fig.7 Flow and mass error of case1 at different combinations ofαandΔt

通过图7可以看出所有α、Δt参数组合情况下耦合求解方法的流量连续性误差均小于0.5%，时间Δt的不同取值几乎对流量连续性误差没有影响。α取值对于流量连续性误差有比较明显的影响，这主要是因为连续性误差的大小主要受到耦合过程中管段过流断面变化的影响，而较高的α值会造成管段过流断面变化速率较快（较高的沉积或冲刷速率会导致沉积物的快增加或降低），从而造成相对较大的流量连续性误差。

对于TSS连续性误差，α、Δt取值对其均有比较明显的影响，并且在α、Δt均取较高值的情况下出现了很高的TSS连续性误差。说明在底泥颗粒浓度高且易于沉降或冲刷的情况下较长的时间步长会导致连续性误差的增加。但是可以看出随着时间步长的缩短，TSS连续性误差快速降低至较低的数值，说明缩小时间步长可以有效应对高浓度且易于沉降或冲刷的底泥颗粒的输运模拟。可以看出在排水系统中，虽然在高浓度、高恢复饱和系数的底泥输运情况下底泥的形变及运动速率有了较大的提升，但是其数值相对于水流速率仍然很低，因此当时间步长长度较短的情况下将每个时间步长内的流动近似为恒定流的前提条件仍然是成立的，因此弱耦合求解方法用于管道底泥输运问题的求解问题的模拟仍然可以满足数值稳定性及低连续性误差的要求。

4.2 案例2模拟结果与分析

在案例2的SWMM5模拟结果与弱耦合求解方法模拟结果对比的过程中，为了使2种不同的模拟方法均达到最佳模拟效果，2种不同模拟方法中的水质模拟相关参数采用不同的取值。不同模拟方法的参数取值如表3所示。

表3 SWMM5及STM模型在耦合及非耦合模拟中的参数取值Tab.3 Parameters in SWMM5 and STM with and without coupling process

2种模拟方法获得的TSS浓度模拟结果对比如图8所示。通过图8可以看出考虑底泥输运的耦合求解方法的模拟结果与实测数据吻合得更好。SWMM5模拟结果的问题主要体现在模拟的后半段TSS浓度模拟值普遍较实测值偏低。这个现象在2011-07-12、2011-07-17以及2011-07-26三天的降雨体现得比较明显，这主要是由于在没有考虑底泥输运情况下，当地面污染物在被雨水冲刷完后，管道水流中的污染物量大大减少，造成TSS浓度非常低。而实际情况下水流对于管道底泥的冲刷会造成水中底泥颗粒仍然维持在一定的浓度。耦合模拟结果由于考虑水流对于管底沉积物的冲刷，因此模拟结果更加接近实测值。

2011-06-24的降雨事件中监测的TSS浓度曲线中有2个峰值，分别出现在0：50以及2：00这2个时刻。SWMM5模拟结果中只模拟出2：00的TSS峰值，而耦合求解方法的模拟结果中2个浓度峰值都有较好的体现。这主要是因为在SWMM5模拟过程中，污染物只来自于地面污染物的冲刷，当降雨强度较低的时候，各个汇水子面积上的地表径流量很小，对地面污染物的冲刷能力很弱，因此地表径流冲刷引入的污染物量几乎对于管道中的TSS浓度没有影响。耦合模拟过程中管道中的流量会在流动的过程中从上游至下游逐渐累加，因此管道内的水流在从起端流至监测点的过程中冲刷能力逐渐变强，并不断对管底沉积物进行冲刷，从而形成比较明显的浓度提升，形成第一个TSS浓度峰值。

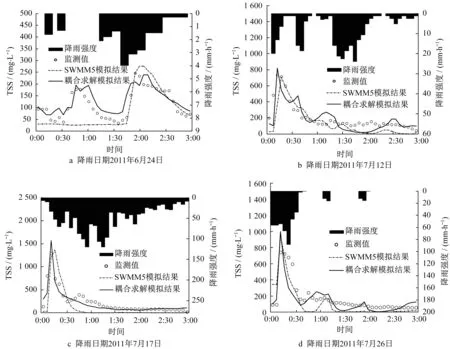
图8 案例2耦合求解方法与SWMM5模拟结果对比Fig.8 Comparison of simulation results with and without coupling process

为了定量检验2种方法模拟结果的质量，对2种方法的模拟结果的纳什效率系数（Nash-Sutcliffe efficiency coefficient，NSE）进行了计算。表4显示了2种方法水质模拟结果的纳什效率系数及流量、污染物连续性误差。

表4 2种求解方法的纳什系数及连续性误差对比Tab.4 Numerical accuracy evaluation of simulation results for each storm event

通过表4可以看出耦合求解方法对应的NSE数值明显较SWMM5的NSE值更高，说明耦合求解方法具有更好的模拟效果，耦合求解方法的连续性误差虽然较SWMM5的连续性误差高，但是仍然在较低且可接受的范围内。

5 结论

以SWMM5软件为基础框架，将Exner方程的求解方法嵌入SWMM5的水力、水质计算过程中，实现SWExner方程组的弱耦合求解。利用该耦合求解方法可以实现在考虑管道底泥输运情况下的管网水力、水质模拟，从而实现在考虑管道底泥输运的情况下，对排水管网的水力、水质工况进行更加准确的模拟和评估。

在该耦合求解过程的每一个时间步长中，Exner方程求解的结果需要利用水流携沙能力进行校验与修正，从而使得SWMM5原有的时间步长确定机制可以用来确定耦合过程的时间步长。通过对SWMM5中填充圆（filled circular）断面类型的改造，实现了在模拟过程中更新断面参数。目前的耦合求解方法中只能对于圆形断面实现断面参数的更新。本文2个案例的管段断面均为圆形，因此可以利用耦合求解方法进行模拟，下一步工作会将SWMM5中的多个断面类型进行改造实现对于沉积物断面在模拟过程中的更新。

通过2个模型案例的模拟，验证了该管道底泥输运模型弱耦合求解方法的数值稳定性及模拟结果的准确性。通过模拟结果可以看出该方法的水流、污染物连续性误差均较小，而且其模拟结果与单纯的SWMM模拟结果相比，与实测的水力、水质数据具有更高的吻合度。