求解大型稀疏线性方程组的贪婪距离随机Kaczmarz方法

杜亦疏，殷俊锋，张 科

（1.同济大学数学科学学院，上海200092；2.上海海事大学文理学院，上海201306）

考虑求解具有如下形式的大规模稀疏线性方程组

其中系数矩阵A∈Rm×n可为满秩或秩亏矩阵，且b∈Rm.当线性方程组（1）不相容时，通常考虑求其最小二乘解

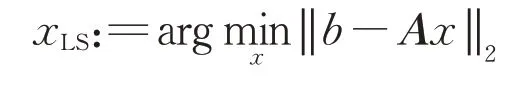
当线性方程组（1）相容时，通常考虑求其最小欧氏范数解

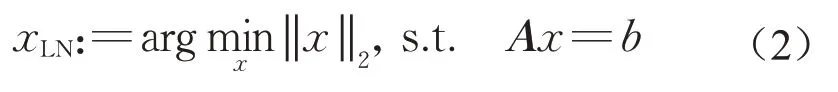
问题（2）等价于求解等价的正规方程组

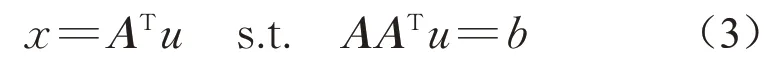
为了求解大型稀疏线性方程组（1），许多经典的迭代方法陆续被提出来并加以深入研究，例如，Kaczmarz迭代方法［1］、超松弛迭代方法（SOR）［2-3］、共轭梯度法（CG）［4］、广义极小残量法（GMRES）［5］和稳定化的双共轭梯度法（BiCGSTAB）［6］等.关于这些迭代法理论及其应用的综述，参见文献［7-13］.

自从20世纪30年代波兰数学家Stefan Kaczmarz提出Kaczmarz方法后，该方法迅速得到数值计算专家和学者的广泛关注，其迭代方法的各种变体和收敛理论获得了大量的研究和发展［14-15］.由于该方法是一种具有代表性的行处理迭代方法，其行投影方法很容易在计算机上实现和并行计算，因此被广泛应用在分布式计算、电子计算机断层扫描、数字信号处理、人工智能和图像恢复等科学与工程计算领域［16-20］.

Strohmer和Vershynin［21］在2009年首次提出采用随机的思想来选取工作行，并证明了这种随机Kaczmarz方法具有线性收敛速率，这再度使得Kaczmarz方法成为数值代数领域的一个研究热点.Bai等［22］结合贪婪和随机的数学思想，提出了一种新的且更加有效的概率准则来选取工作行，即贪婪随机Kaczmarz方法.此后，松弛贪婪随机Kaczmarz方法［23］和部分随机拓展的Kaczmarz方法［24］也被陆续提出并加以深入研究.Popa［25］总结了各类Kaczmarz方法的收敛速率.更多的随机Kaczmarz方法及其理论可以参见文献［26］.另一方面，Bai等［27］利用同样的数学思想，提出了一类贪婪随机坐标下降方法，用以求解列满秩超定线性代数方程组的最小二乘问题，可以证明新方法较原有的随机坐标下降方法［28］具有更快的收敛速率.

在研究中发现，提高随机Kaczmarz方法收敛速率的重点在于能否提出一类从系数矩阵中选取工作行的有效概率准则.在原始的Kaczamrz方法中，工作行被循环选取，然后将当前点投影到工作行所形成的超平面上.在文献［29］中，贪婪Kaczmarz方法的工作行选取办法被分为两类，第一类是选取上一次迭代后各残差分量中模长最大的行作为本次迭代的工作行，第二类是选取当前迭代解离系数矩阵各行所形成的超平面的距离最大的行作为本次迭代的工作行.受该思想启发，笔者提出一类基于距离的贪婪随机Kaczmarz方法（GDRK）.

1 贪婪距离随机Kaczmarz方法

在原始的Kaczmarz方法中，工作行被循环选取，然后将当前点投影到工作行所形成的超平面上，更具体地说，如果定义A()i代表系数矩阵A的第i行，b()i代表向量b的第i个分量，初始向量为x0，则Kaczmarz方法如算法1所示.

算法1［1］Kaczmarz方法.①置k：=0.计算i k=(kmodm)+1.②计算x k+1=x k+③置k=k+1，转步骤①.其中，(⋅)T代表矩阵或向量的转置.在Kaczmarz方法中，通过按顺序选取工作行，然后将当前点x k正交投影到超平面A(i k)x k=b(i k)上.

在文献［14］中，Ansorge首次采用贪婪的思想来选取工作行，即选取上一次迭代后各残差分量中模长最大的行作为本次迭代的工作行，提出贪婪残差Kaczmarz方法，并将Cimmino方法与Kaczmarz方法的联系做了详尽的分析，具体过程见算法2.

算法2［14］贪婪残差Kaczmarz方法.①置k：=0.计 算i k=arg maix②计算x k+1=x k+③置k=k+1，转步骤①.

Nutini等［29］采用另一类贪婪选取工作行的办法，即选取当前迭代解离系数矩阵各行所形成的超平面的距离最大的行作为本次迭代的工作行，提出贪婪距离Kaczmarz方法.论文分析收敛性并尝试利用正交图提出快速的随机Kaczmarz方法，具体过程见算法3.

算法3［29］贪婪距离Kaczmarz方法.①置k：=0.计 算i k=arg maix②计算x k+1=x k+③置k=k+1，转步骤①.

在文献［21］中，Strohmer和Vershynin将各行2-范数与‖ ‖AF比值的平方作为概率，然后根据此概率随机选取本次迭代的工作行，提出随机Kaczmarz方法，具体过程见算法4.

算法4［21］随机Kaczmarz方法.①置k：=0.根据概率Pr(row=i k)=选取指标i k∈{1，2，…，m}.②计算x k+1=x k+③置k=k+1，转步骤①.

在算法4中，Pr(⋅)代表选取系数矩阵第i k行作为本次迭代工作行的概率.

关于随机Kaczmarz方法，有如下的收敛性定理.

定理1［21-22］线性方程组（1）相容，其中系数矩阵A∈Rm×n且右端项b∈Rm.初始向量x0∈Rn在AT的列空间中，则通过随机Kaczmarz方法生成的迭代序列在期望上收敛到其最小范数解x⋆=A†b，且迭代解序列的误差的数学期望满足

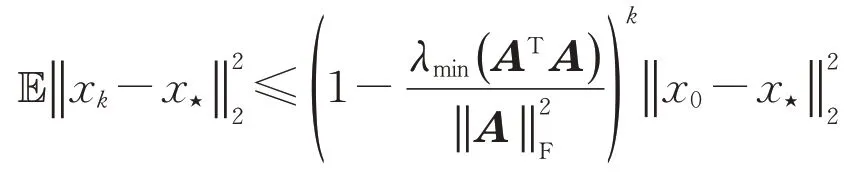
Bai等［22］提出了一种新的概率准则，即先选取当前点x k离系数矩阵各行所形成的超平面的距离较大的行所对应的指标i k，将其放入集合U中，然后定义集合U中每行被选取的概率为各残差分量模长的平方除以残差欧式范数的平方，具体过程见算法5.

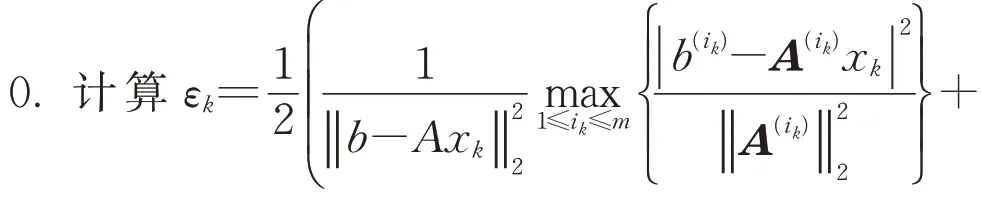
算法5［22］贪婪随机Kaczmarz方法.①置k：=②定义正整数指标集U k=A(i k)x k|2≥εk‖ ‖b-A x k③计算的第i个分 量=④根据概率Pr(row=i k)=选取指标i k∈U k.⑤计算x k+1=x k+⑥置k=k+1，转步骤①.

关于贪婪随机Kaczmarz方法，有如下的收敛性定理.

定理2［22］若线性方程组（1）相容，其中系数矩阵A∈Rm×n且右端项b∈Rm.初始向量x0∈Rn在AT的列空间中，则通过贪婪随机Kaczmarz方法生成的迭代序列在期望上收敛到其最小范数解x⋆=A†b，且迭代解序列的误差的数学期望满足

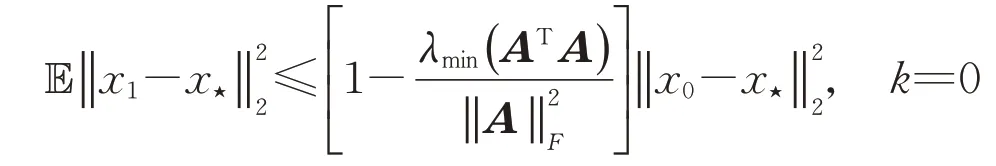
和

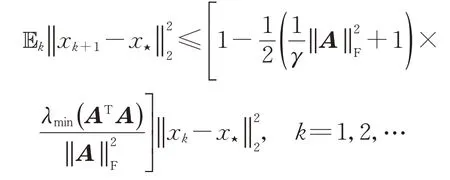
其中γ=更一般地有

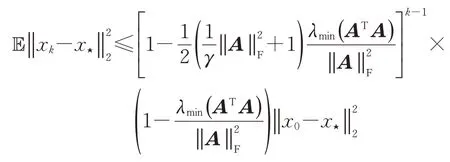
在算法5中，希望指标集U k中对应较大距离的指标i k可以以较大概率被取到.然而在算法5的第④步，选取指标i k的概率定义为正比于各残差分量模长的平方.假设集合中指标i k所对应的行具有较大残量，则它有较大概率被取为工作行；若同时该指标对应的行范数很大，则当前点投影到此工作行所形成的超平面的距离较小，这与算法5第②步中指标集U k的定义相矛盾，此时需要对这2个条件进行平衡.在该想法的启发下，提出基于距离的贪婪随机Kaczmarz方法，具体过程见算法6.

算法6贪婪距离随机Kaczmarz方法.①置k：=0.计算

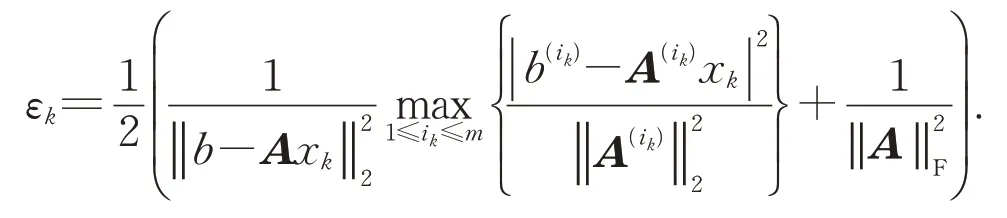
②定义正整数指标集

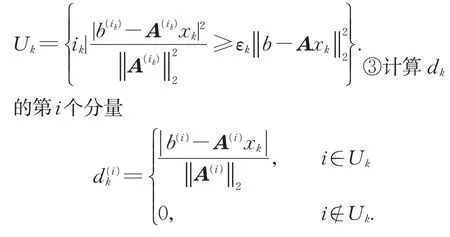
④根据概率Pr(row=i k)=选取指标i k∈U k.⑤计算x k+1=x k+置k=k+1，转步骤①.

由于当前点x k到所有系数矩阵行所形成的超平面的最大距离平方满足下式：

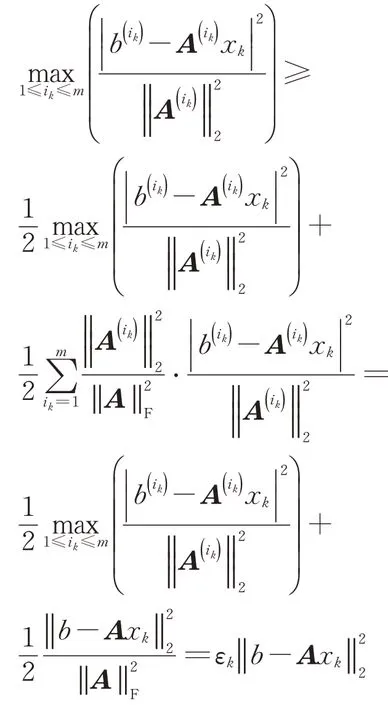
可知算法6中步骤②指标集U k非空，具体参见文献［22］.

由于计算残量具有如下递推式：

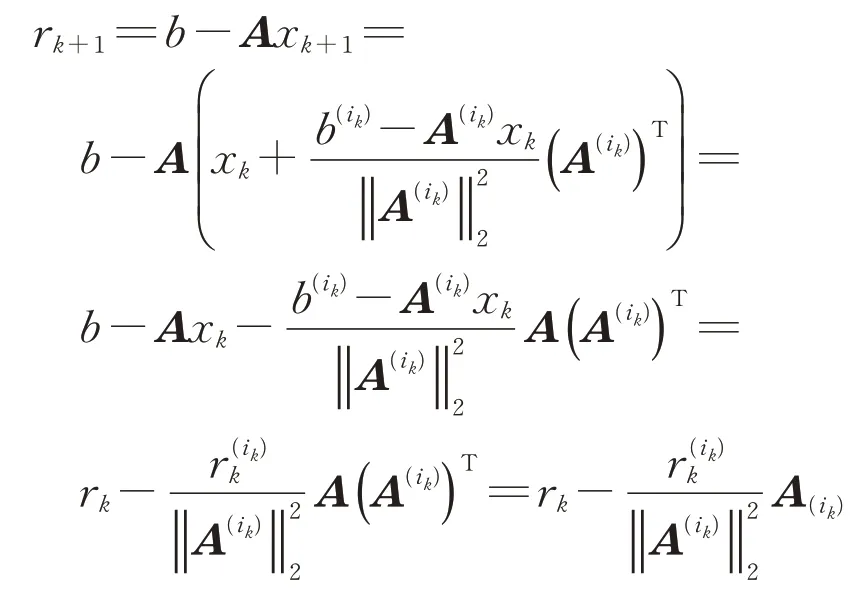
其中B=AAT且B(i k)表示矩阵B的第i k列.也就是说，如果在迭代之前已知AAT，可以进一步提高贪婪距离随机Kaczmarz方法的运行效率，参见文献［22］.关于采用随机策略近似计算矩阵AAT，参见文献［30］.

2 贪婪距离随机Kaczmarz方法的收敛性分析

首先说明若贪婪距离随机Kaczmarz方法收敛，则其一定可以收敛到最小范数解.假设x⋆为满足相容 系 统（1）的 最 小 范 数 解，由（2）可 知，x⋆≜A†b∈R(AT)，其中，R(AT)表示AT列空间.另一方面，若初始向量x0在AT列空间中，由算法6中步骤⑤可知，算法6生成的迭代序列一定在AT列空间中，故若算法收敛，则一定收敛到相容系统（1）的最小范数解.

关于贪婪距离随机Kaczmarz方法，有如下的收敛性定理.

定理3若线性方程组（1）相容，其中系数矩阵A∈Rm×n且右端项b∈Rm.初始向量x0∈Rn在AT的列空间中，则通过贪婪随机Kaczmarz方法生成的迭代序列在期望上收敛到其最小范数解x⋆=A†b，且迭代解序列的误差的数学期望满足

证明：由算法6步骤⑤，可得

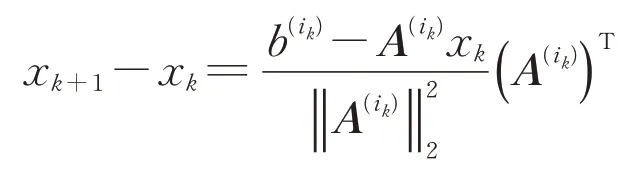
即向量x k+1-x k平行于向量(A(i k))T.又由

可得向量x k+1-x⋆正交于向量(A(i k))T，即正交于向量x k+1-x k，故有下式成立

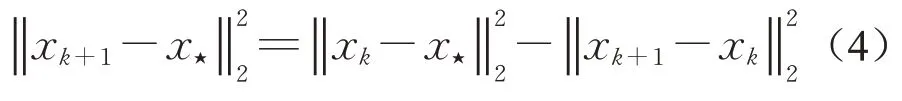
对等式（4）两侧取期望，有

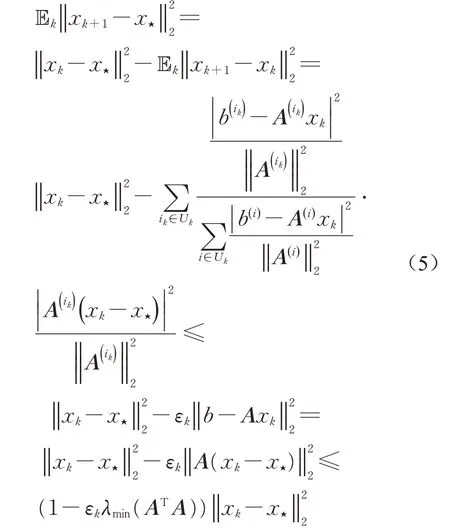
其中，式（5）最后一个不等式需要用到不等式（6），即对于在AT列空间中任意u∈Rn，有

由算法6中εk定义，对于k=1，2，…，有

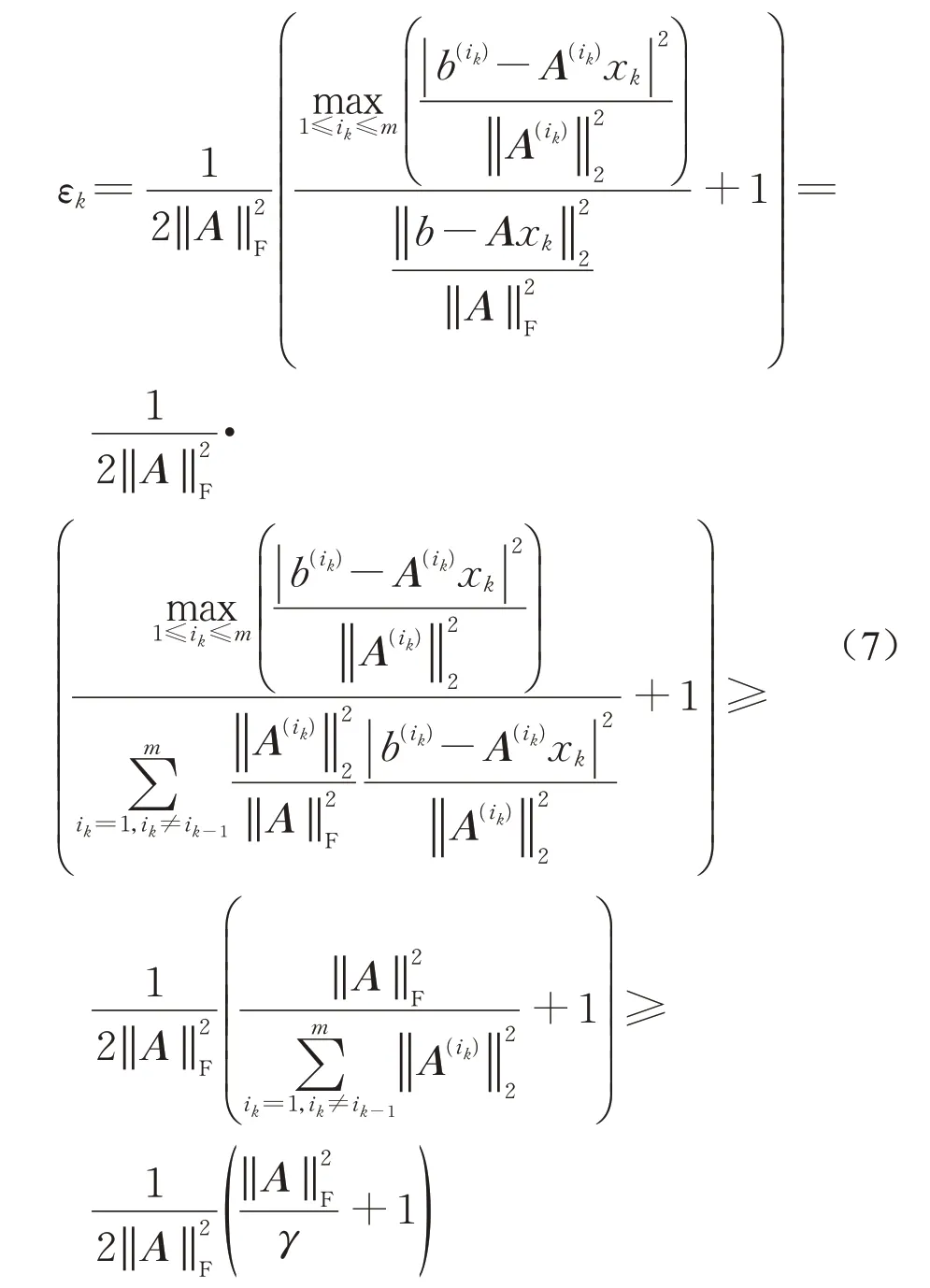
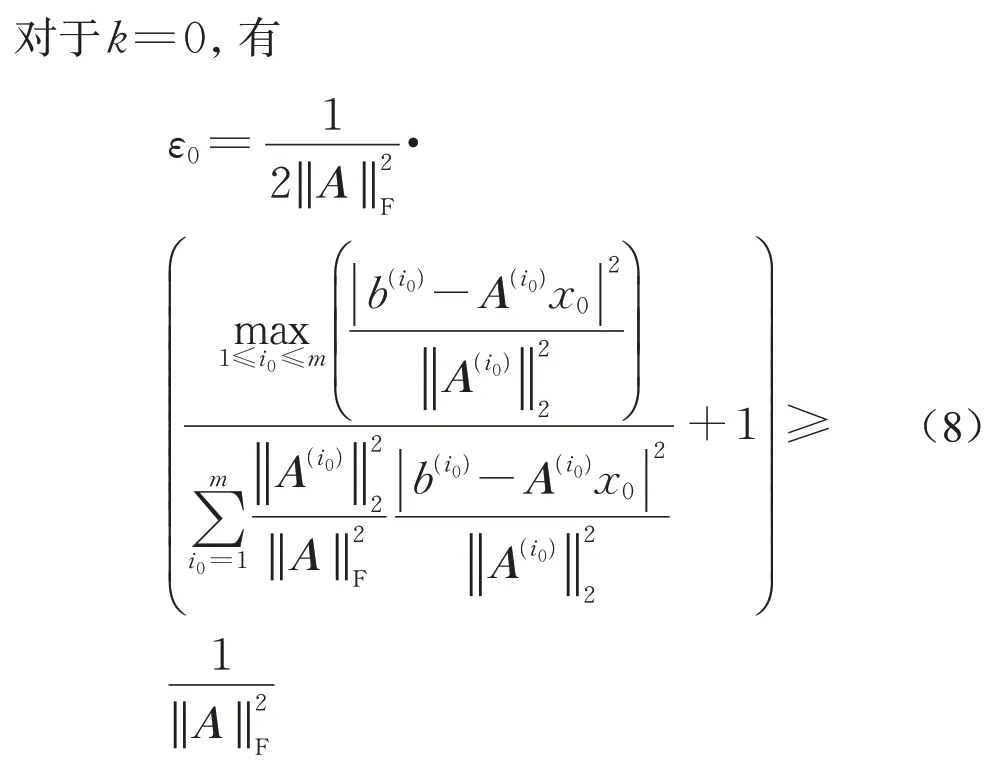
将不等式（7）和（8）代入不等式（5）中，通过归纳法，有

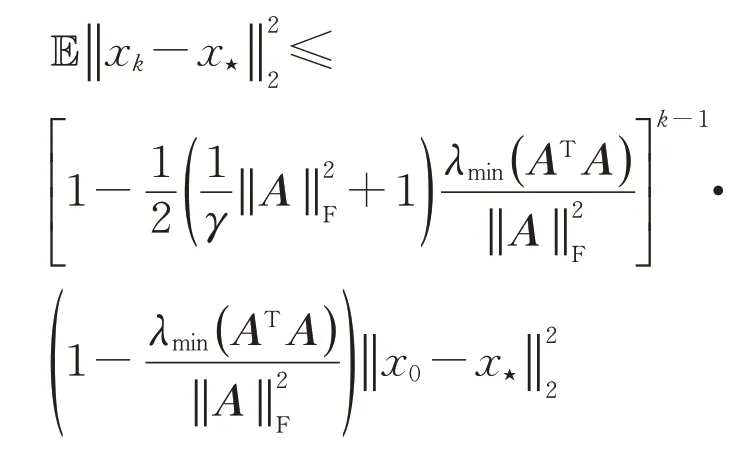
记定理1中随机Kaczmarz方法的收敛因子为

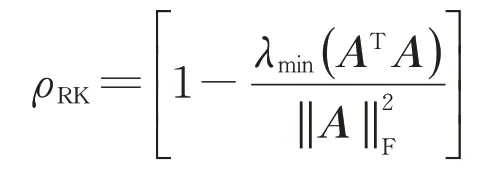
定理2中贪婪随机Kaczmarz方法的收敛因子为

定理3中贪婪距离随机Kaczmarz方法的收敛因子为

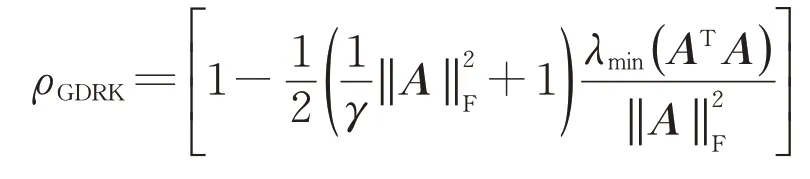
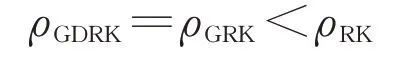
一般而言，收敛因子越小，收敛越快.这里需要特别指出的是，贪婪距离随机Kaczmarz方法和贪婪随机Kaczmarz方法在理论上具有相同的收敛因子，但是对于实际问题，由于贪婪距离随机Kaczmarz方法选取工作行的概率更加符合指标集U k定义，故实际计算时新方法有可能收敛更快.

在浮点运算量方面，随机Kaczmarz方法每次迭代需要4n+1个浮点运算量.若残差由递推公式计算，贪婪随机Kaczmarz方法以及贪婪距离随机Kaczmarz方法每次迭代需要7m+2n+2个浮点运算量［22］.因此，当m＞时，贪婪距离随机Kaczmarz方法计算量小于随机Kaczmarz方法.

3 数值实验

通过数值实验比较随机Kaczmarz方法（RK）、贪婪随机Kaczmarz方法（GRK）、贪婪距离随机Kaczmarz方法（GDRK）的计算效率.这里，迭代步数（IT）和计算时间（CPU）取50次计算结果的中位数.

实验中，通过MATLAB函数randn随机生成解x∈Rn，右端项b∈Rm由A给出，通过MATLAB函数pinv计算最小范数解x⋆=A†b.此外，需要指出GRK方法与GDRK方法按照算法5和6中定义的过程精确执行，并没有显式地计算矩阵B=AAT来计算残量.在本节的所有数值实验中，均取初始向量为x0=0，停机准则为近似解的相对误差

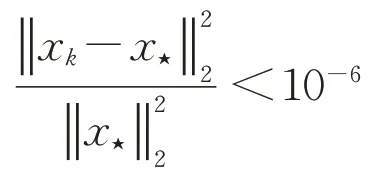
或者迭代步数超过20万步.在实验表格中，若在20万步内未达到指定精度，即用′--′表示.

相关信息见表1～4.表1和表3给出了测试矩阵的阶数、稠密度、秩和条件数，其中稠密度定义为矩阵非零元个数除以矩阵元素个数.关于GDRK方法对于RK方法的加速比，其定义为RK方法所需的计算时间除以GDRK方法所需的计算时间.所有测试矩阵都来自于佛罗里达稀疏矩阵集，见参考文献［31］.

例1.表1列出了测试的方阵的相关信息.包含满 秩 矩 阵Trefethen_150、cage5、Trefethen_300、Stranke94和秩亏矩阵Sandi_authors.其中，矩阵Trefethen_150、Trefethen_300、Stranke94、Sandi_authors为对称矩阵，矩阵cage5为非对称矩阵.

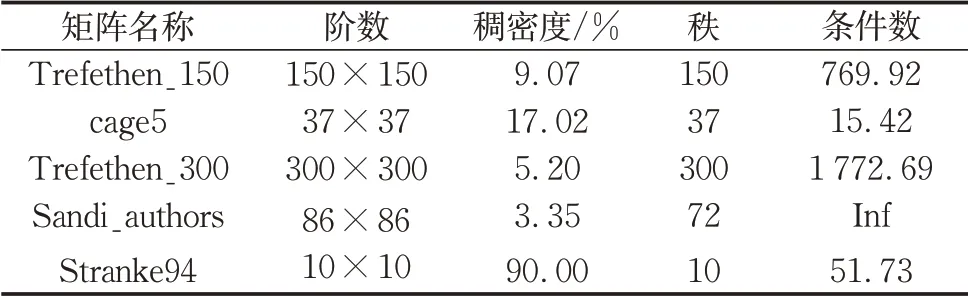
表1 方阵信息Tab.1 Information of square matrices for Example 1

对于测试的方阵，表2给出了RK、GRK、GDRK三种方法的迭代步数（IT）与计算时间（CPU）.

表2 方阵数值结果Tab.2 Numerical results of square matrices for Example 1

从表2可以看出，GDRK与GRK方法总能计算出符合精度的解，而RK方法有时在迭代步数达到20万步后仍不能计算出符合精度的解.而且即便RK方法收敛，GDRK与GRK方法在迭代步数与计算时间上也均少于RK方法.此外，GDRK方法进一步优化了GRK方法，其关于RK方法迭代时间的加速比最大可以达到36.80（矩阵cage5），最小可以达到2.20（矩阵Stranke94）.因此，无论对于满秩还是秩亏的方阵，GDRK方法均收敛，且其迭代步数与计算时间均优于传统的RK方法与GRK方法.

图1和图2是近似解的相对误差与迭代步数的关系.

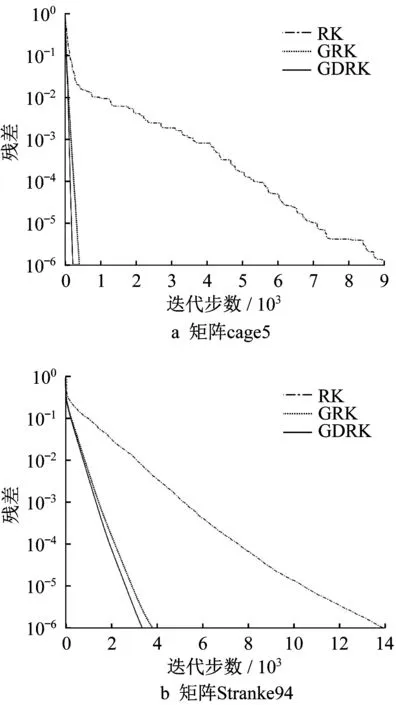
图1 例1近似解的相对误差随着迭代步数的变化曲线Fig.1 Relative solution error with the change of IT for Example 1

图1描绘了矩阵cage5（左）和Stranke94（右）的近似解的相对误差随着迭代步数变化的曲线，进一步验证了GDRK方法比经典的RK方法收敛更快.

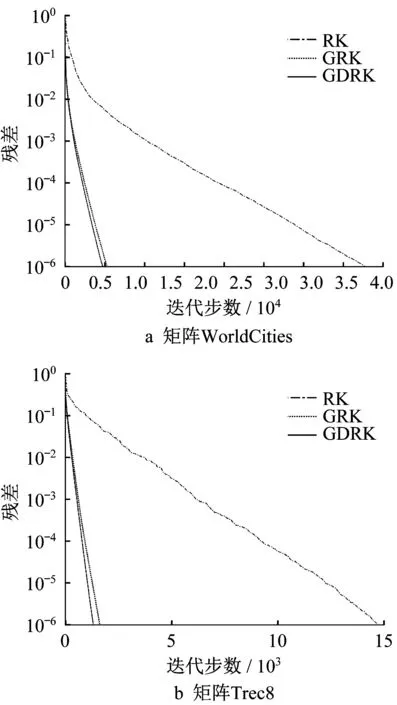
图2 例2近似解的相对误差随着迭代步数变化的曲线Fig.2 Relative solution error with the change of IT for Example 2

例2.表3列出了测试的长方形矩阵的相关信息.包含行满秩矩阵refine、bibd_13_6、Trec8、列满秩矩阵WorldCities和秩亏矩阵GL7d26.

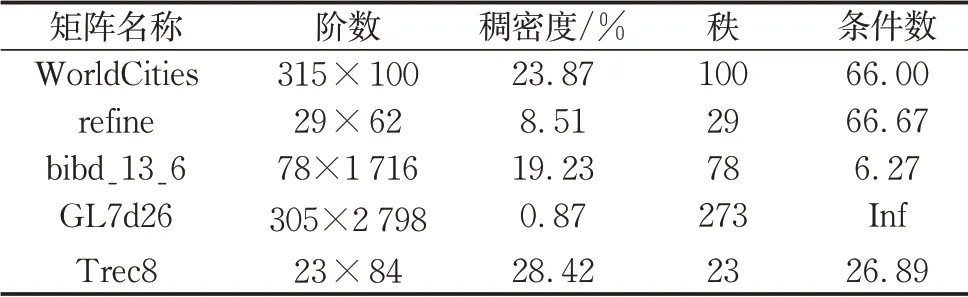
表3 长方形矩阵信息Tab.3 Information of rectangular matrices for Ex⁃ample 2

对于测试的长方形矩阵，表4给出了RK、GRK、GDRK三种方法的迭代步数（IT）与计算时间（CPU）.

从表4可以得出和例1类似结论，即GDRK与GRK方法总能计算出符合精度的解，而RK方法有时在迭代步数达到20万步后仍不能计算出符合精度的解.而且即使RK方法收敛，GDRK与GRK方法在迭代步数与计算时间上也均少于RK方法.此外，GDRK方法进一步优化了GRK方法，其关于RK方法迭代时间的加速比最大可以达到57.23（矩阵refine），最小可以达到4.12（矩阵bibd_13_6）.因此，无论对于满秩或秩亏的长方形矩阵，GDRK方法均收敛，且其迭代步数与计算时间均优于传统的RK方法与GRK方法.

表4 长方形矩阵数值结果Tab.4 Numerical results of rectangular matrices for Example 2

图2 描绘了矩阵WorldCities和Trec8的近似解的相对误差随着迭代步数变化的曲线，进一步验证了GDRK方法比经典的RK方法收敛更快.

4 结论

提出一类贪婪距离随机Kaczmarz方法，理论分析证明新方法的收敛性，且收敛因子小于传统的随机Kaczmarz方法的收敛因子.数值实验结果表明所提出的新方法在迭代步数和计算时间上均优于传统的随机Kaczmarz方法以及贪婪随机Kaczmarz方法.贪婪距离随机Kaczmarz方法能够快速求解大规模稀疏相容线性方程组，主要原因在于新方法定义的随机选取工作行的概率更符合指标集合的定义.如何随机选取工作行以加速随机Kaczmarz方法仍然是一个值得研究的问题.