电动汽车电池组内部绝缘故障研究

陈照添,刘成沛

(中南大学 机电工程学院,湖南 长沙,410083)

电动汽车的研究与使用为环境保护做出了较大的贡献,颇受人们的期待,而电动汽车出行的一些安全事故与问题倍受关注与争议,如自燃、漏电等安全问题，因此，对动力电池内部的绝缘状况进行监测与诊断、防止出现漏电现象有着重要的研究意义。在当前阶段,对车载绝缘进行实时检测的方法主要为2个大类型:有源式以及无源式。无源式类型的检测方法是在电路中设置偏置电阻,采集偏置电阻在接入前后的电压,以此计算绝缘电阻,但偏置电阻的引入会影响电池对地的绝缘情况[1]。有源式检测方法是向电池高压回路注入一定的电压波形,利用前后所得的电压采样值计算绝缘电阻[2]。目前,有多种类型的电动汽车绝缘电阻模型设计和检测方法,主要研究动力电池包整体的高压绝缘的检测,测量动力电池包的正极与负极对底盘的绝缘电阻,以减小出现漏电危害的问题,而对电池包的内部绝缘状态检测与故障定位的研究较少[3]。动力电池包的内部有较多的电池单体、结构部件以及连接组件等,也可能出现某个位置的漏电问题,对电池的使用寿命和行车安全造成影响。

确定发生绝缘故障问题的位置是进行故障维修处理的关键环节,考虑到绝缘性能的渐变性,发生绝缘故障问题常是由单点绝缘薄弱引起的[4]，因此,对电池包的内部进行单点绝缘故障问题的监测,确定发生绝缘故障的位置,能对电池包的内部发生绝缘故障问题前进行及时的报警,防止漏电危害、发热现象等问题的出现及其恶化,维修人员能根据故障报警和故障定位信息及时地进行相应的故障处理,减少因电池包的内部出现绝缘故障问题而带来的安全影响与经济损失。基于有源式的对地电阻检测原理,采用注入电压法计算电池组单点绝缘故障电阻,定位发生单点绝缘故障的位置,建立计算模型,通过相应的理论推导以及MATLAB仿真,对该方法的计算误差进行合理分析。

1 电池组单点绝缘故障计算模型

1.1 单点绝缘故障物理模型

考虑到电池组内部的绝缘问题及其结构,可得如图1所示的分布式绝缘电阻模型,动力电池包与电池模组之间、电池模组与电池单体之间均可视为此模型。其表示在无绝缘故障问题的电池组中,每个电池的正、负极都有1个与车身接地的绝缘电阻,2个相串联的电池之间用1个绝缘电阻表示[5],若电池组内有n个电池则有n+1个绝缘点,R1表示电池组负极与车身接地的绝缘电阻,Rn+1表示电池组正极与车身接地的绝缘电阻,R2～Rn为表示各个串联电池之间的绝缘电阻,U1表示电池组负极与车身接地之间的电压,U2表示电池组正极与车身接地之间电压。

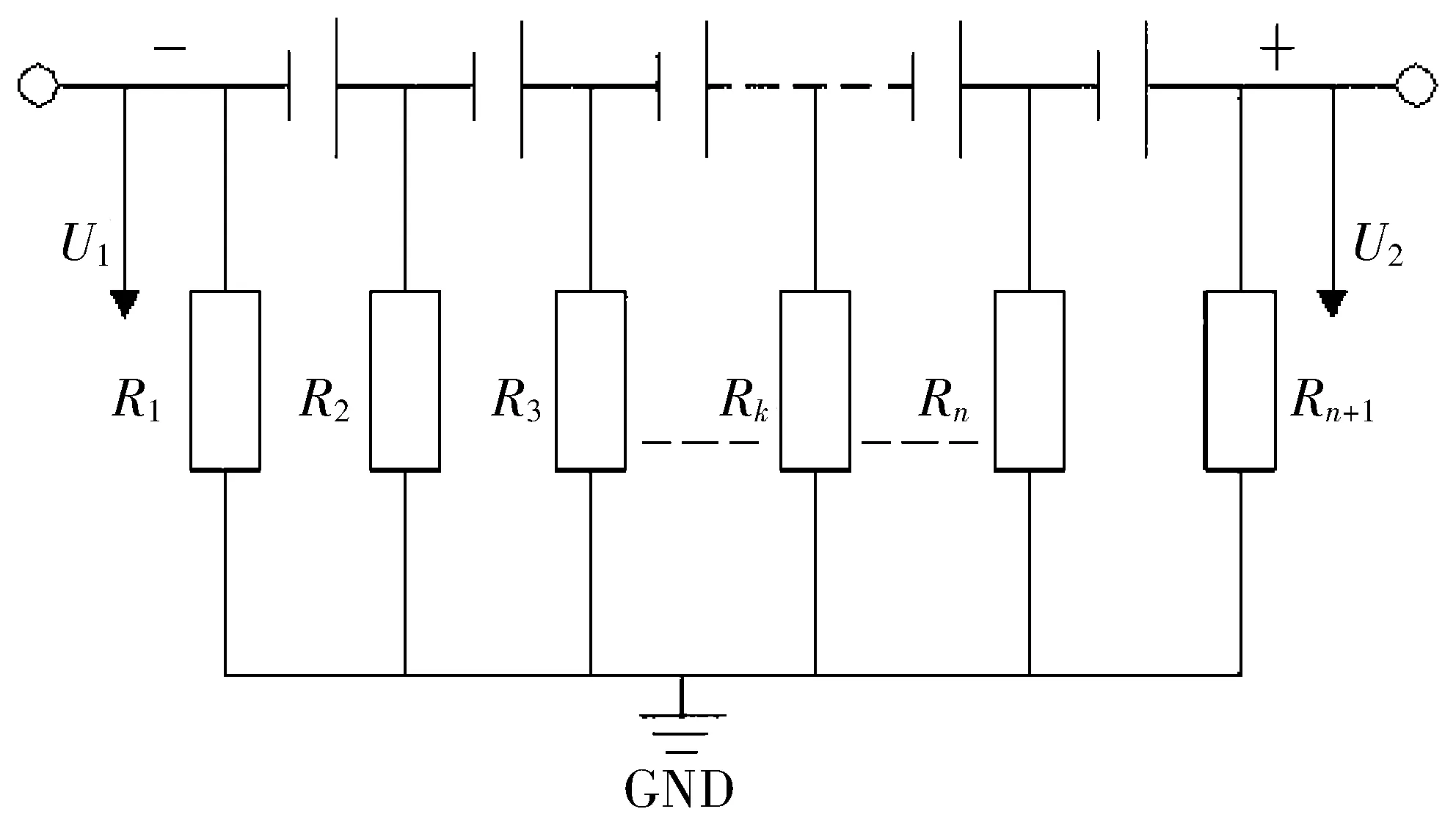
图1 分布式绝缘电阻模型

上图1所示,若电池组没有出现绝缘故障问题,即没有出现漏电现象或漏电流，则可忽略不计,电阻R1～Rn+1阻值较大。若电池组内某一点出现绝缘故障问题,如k点,则其电阻Rk远小于其他位置的绝缘电阻,其他各点位置的绝缘电阻均可视为无穷大[6]，可得电池组内部单点漏电模型如图2所示。图2中k点为出现绝缘故障的位置,Rk为绝缘故障电阻,U为电池组整体电压,U1为绝缘故障电阻Rk到电池组负极的电压。

图2 电池组内部单点漏电模型

1.2 单点绝缘故障检测模型

根据上述的物理模型分析,采用电压注入法检测电池组内部发生绝缘故障问题的位置及其电阻,如图3、图4所示。在此模型中,Rk为绝缘故障电阻,U1为电池组负极到绝缘故障电阻Rk的电压,U2为电池组正极到绝缘故障电阻Rk的电压,U0是绝缘电阻Rk对测量地的电势,R1与R2为已知、不随环境变化的电阻,Ra为采样电阻,Ua为采样电阻Ra测量所得的电压,Us为注入信号电压。

图3 绝缘电阻故障检测模型(1)

1)当注入+20 V电压时,检测模型的电流流向如图3所示,可得下列关系:

(1)

(2)

(3)

U=U1+U2

(4)

2)当注入-20 V电压时,检测模型的电流流向如图4所示,可得下列关系:

图4 绝缘电阻故障检测模型(2)

(5)

(6)

(7)

在上述公式中,未知的量有Ιk1，Ιk2，Uo1，Uo2，Rk，U1和U2,已知的量有R1，R2，Ra，Us1，Us2，Ua1，Ua2和U,由公式(1)，(2)，(5)和(6)可得:

(8)

由公式(1)，(3)，(4)，(5)，(7)和(8)可得:

(9)

(10)

(11)

规定X为电池组内部的绝缘故障点距离其负极的百分比位置,其中U是已知量,根据公式(10)可得:

(12)

2 计算模型误差分析

2.1 各参数对绝缘故障电阻的影响

由公式(11)可知,绝缘故障电阻Rk是由定值电阻R1，R2以及采样电阻Ra、采样电阻Ra测量所得的电压Ua、注入的信号电压Us经公式计算而来,可知Rk的计算精度受采样电阻、采样电阻的电压、定值电阻精度的影响。设采样电阻Ra的理论值与实际值相对误差为零,定值电阻R1和R2的理论值与实际值相对误差为零,采样电阻Ra测量所得的采样电压Ua1的相对误差为γua1,Ua2的相对误差为γua2,注入电压Us1的相对误差为γus1,Us2的相对误差为γus2,绝缘故障电阻Rk的相对误差为γRk。由计算Rk的公式可知,可把Us1，Us2，Ua1和Ua2当成变量,则Rk可表示为

Rk=f(us1,us2,ua1,ua2)

(13)

根据误差传播理论结合公式(11)得:

(14)

其中：

由式(14)可知,采样电压Ua相对误差(γua1、γua2)、注入电压Us相对误差(γus1、γus2)对绝缘故障电阻Rk的相对误差γRk有较大的影响,因此,要提高绝缘故障电阻的测量精度,需要提高采样电压的测量精度和注入电压的精度。此外，应选择精度等级高的定值电阻和采样电阻,从而减小绝缘电阻测量的误差。

2.2 各参数对绝缘故障位置的影响

公式(12)中电池组内部的绝缘故障点位置X与电池组电压U、采样电压、注入电压、定值电阻有关,设定值电阻(R1、R2)的实际值和理论值没有误差,电池组电压U的相对误差为γu,采样电压Ua1的相对误差为γua1,Ua2的相对误差为γua2,注入电压Us1的相对误差为γus1,Us2的相对误差为γus2,绝缘故障点位置X的相对误差为γx。由计算X的公式可知,可把U，Us1，Us2，Ua1和Ua2当成变量,根据误差传播理论结合公式得:

(15)

其中

由式(15)可知,采样电压Ua相对误差(γua1、γua2)、注入电压Us相对误差(γus1、γus2)、电池组电压U相对误差(γu)越大,则绝缘故障点位置X相对误差γx越大。

2.3 绝缘故障电阻值误差分析

由公式(11)可知,绝缘故障电阻Rk可由注入电压、采样电压、采样电阻、定值电阻计算得到；由式(15)可知,绝缘故障电阻Rk相对误差γRk与采样电压Ua相对误差(γua1、γua2)和注入电压Us相对误差(γus1、γus2)有直接关系,假设2组采样电压Ua的相对误差相等,记γua1=γua2=γua；2组注入电压Us的相对误差相等,记γus1=γus2=γus,则可得:

(16)

其中：

由式(16)可知,采样电压Ua相对误差(γua)、注入电压Us相对误差(γus)越大,则绝缘故障电阻Rk相对误差γRk越大。取γua=1%,γus=1%,联合式(16)，(11)和(12)进行MATLAB仿真分析,得出结果如表1所示。

表1 绝缘电阻计算值误差分析

表1中的阻值计算误差均是相对误差,对表1中数据进行分析可得出如下结论:

1)绝缘故障电阻Rk在一定的情况下,若发生绝缘故障的位置X离电池组中点越近,则电阻计算误差会越大。

2)在相同位置X发生绝缘故障问题,绝缘电阻较大或较小,电阻计算误差都会增大。

2.4 绝缘故障定位误差分析

由公式(12)可知,绝缘故障点位置X可由电池组电压、采样电压、注入电压、定值电阻计算得到；假设两组采样电压Ua相对误差相等,记γua1=γua2=γua,两组注入电压Us相对误差相等,记γus1=γus2=γus,结合公式(15)和(16)可得:

(17)

其中：

由式(17)可知,绝缘故障电阻Rk的相对误差γRk越大,则绝缘故障点位置X相对误差γx越大。取γua=1%,γua=1%,γu=1%,联合式(17)，(11)和(12)进行MATLAB仿真分析,得出结果如表2所示。

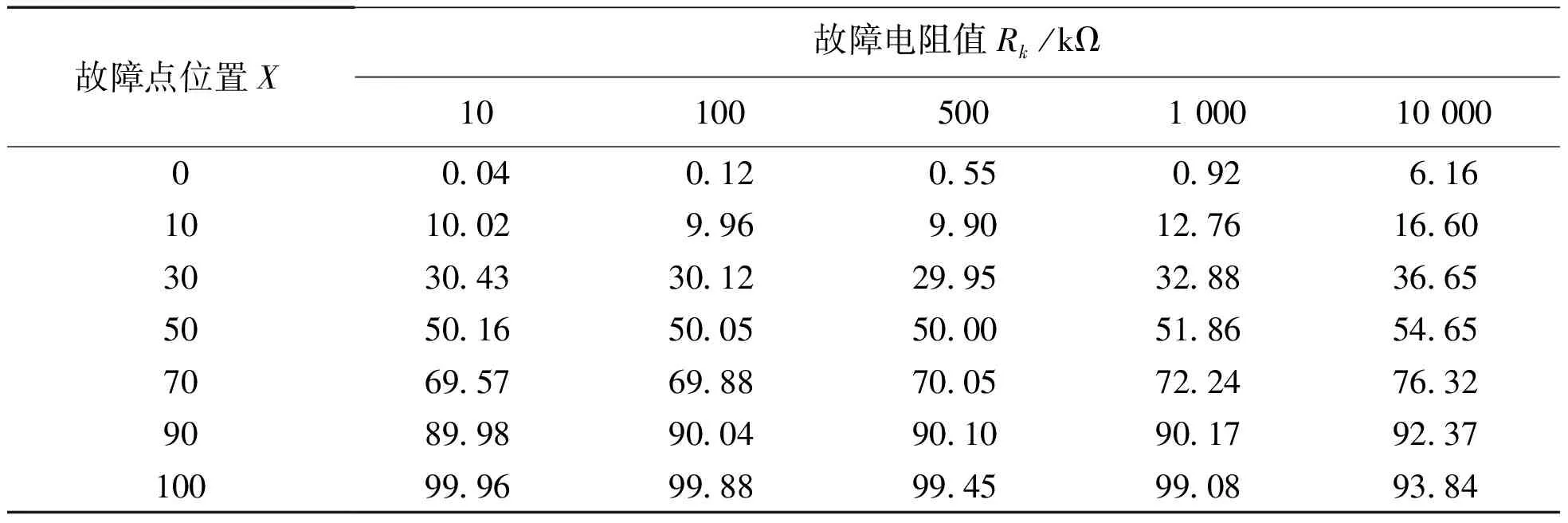
表2 绝缘故障电阻定位误差分析

表2中的电阻定位误差为距离电池组负极的百分比位置,对表2中数据进行分析可得出如下结论:

1)绝缘故障电阻Rk在一定的情况下,发生故障的位置X离电池组正负两极越近,则电阻定位计算误差越大。

2)在相同位置X发生绝缘故障,绝缘电阻较小时,故障定位计算误差较小。

3 实验分析

为验证该诊断模型的有效性和绝缘故障定位的准确性,进行实验室静态试验。电动汽车在停止状态时,电池组没有充放电电流,此时电池组处于静态工作环境。模拟无电流的高压回路,搭建静态试验台,参数如表3所示。

表3 绝缘故障定位静态试验台参数

在上述绝缘试验台中,在电池组的不同位置设计不同大小的绝缘电阻,进行测试分析,如表4所示。

表4 绝缘故障定位静态测试结果

表4中的Rk和X分别表示注入的绝缘电阻及其距离电池组负极的百分比位置,Rkc和Xc分别为检测得出的绝缘电阻和故障位置,γR为绝缘电阻计算值的相对误差,EX为绝缘故障定位的偏移量。

如表4所示,当绝缘电阻较小,阻值计算误差较大,即绝缘电阻Rk=10 kΩ时,绝缘阻值计算误差最大为30%,并且在1 000 kΩ绝缘阻值以内,绝缘电阻越大,阻值计算误差越小。对于绝缘故障定位,在1 000 kΩ绝缘电阻以内,电阻定位计算的误差影响较小,在试验台的100串电池中,定位偏移了1%即偏移了1个电池。并且这些试验结果也与前面误差分析结果相吻合。

4 结论

基于注入电压法,建立了电动汽车电池组内部绝缘电阻故障检测与定位模型,该计算模型仅需2个偏置电阻、1个采样电阻以及1个注入信号电压便可进行采样计算。结合理论分析与推导。以及MATLAB仿真,分析了该模型的计算误差和系统误差。最后通过台架实验,验证了该检测模型的有效性。