基于LM_RBF-PID的板球系统轨迹控制*
黄文杰,向凤红,毛剑琳
(昆明理工大学信息工程与自动化学院,云南 昆明 650500)
1 引言
板球系统作为典型的多输入多输出系统,具有欠驱动、耦合性和非线性强等特点[1],对其控制算法的优化可有效提高板球系统的定位控制和轨迹跟踪的控制精度。尽管PID控制器[2]凭借结构简
单、可靠性高的特点在工程应用中被广泛使用,但在板球系统这一类非线性控制系统中很难达到控制要求[3,4]。因此,国内外学者提出了自适应控制策略[5]、T-S模糊控制[6]、H2控制器和鲁棒性较强的H∞控制器[7]等方案,推动了板球系统理论研究的发展。近年来,随着人工智能研究的不断深入,遗传算法[8,9]、蚁群算法[10]、粒子群算法等近代启发式优化算法相继在板球系统上得到应用。从仿真结果上看,无论是小球的轨迹震荡情况还是控制时间的长短,都得到了一定程度的改进,说明这些语法结构简单和运算能力较强的智能算法均具有一定的应用可行性。
目前板球系统的研究情况大多停留在理论论证方面,将可行方法应用在实物实验的轨迹跟踪的文献较少。本文选取深圳固高科技公司自主研发的GBP2001型板球系统作为研究对象,研究了板球系统的方形轨迹跟踪控制问题;将径向基函数RBF(Radical Basis Function)神经网络与经典PID控制相结合,引入动量因子改进RBF-PID控制算法,用LM(Levenberg-Marquardt)算法代替梯度下降法整定PID控制参数,以解决板球系统稳定性差、运动轨迹复现度差等问题。本文将该参数调整过程命名为LM_RBF-PID控制算法。LM算法具有局部收敛性,同时有鲁棒性强的特点[11],在整定PID控制参数方面得到成功应用[12]。但是,结合自适应控制,针对板球系统这一类非线性控制系统的应用工作尚属首次,本文采用RBF-PID控制算法和LM_RBF-PID控制算法分别在GPB2001型板球系统完成轨迹跟踪控制实验,实验结果对比分析表明,LM_RBF-PID控制算法具有更好的控制效果。
2 GBP2001板球系统建模
在GBP2001板球系统中,以球盘中心作为坐标原点(0,0)建立坐标系,如图1所示。o′x′y′z′是世界坐标系,oxyz是球板的运动坐标系,z轴始终与球盘垂直,x轴和y轴始终与球盘平面平行,o与o′重合。

Figure 1 Ball and plate system coordinate definition schematic diagram图1 板球系统坐标定义示意图
由图1可知,板球系统包括小球位置坐标(x,y)、球板转动角度(θ,β)4个自由度,由于其复杂的非线性特性,难以获取其精确的数学模型,建模过程中在不影响系统特性的情况下做以下假设:
(1)小球在平板上无滑动和绕小球垂直中心轴旋转的运动[13];
(2)忽略平板倾斜角度的限制以及平板面积的影响;
(3)小球在平板上始终和平板保持接触状态;
(4)小球和平板之间所有摩擦忽略不计;
(5)板体在x、y轴方向上关于其支撑点对称并控制两轴的机械条件相同。
分别在x、y2个方向对平板上的小球运动完成解耦,得出x方向和y方向的二维分解示意图,如图2所示。
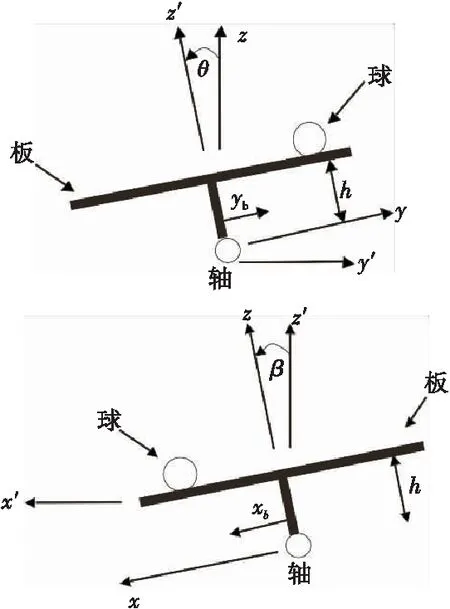
Figure 2 Two-dimensional decomposition of ball and plate system图2 板球二维分解示意
经分析,建立以拉格朗日法为基础的板球系统数学模型,板球系统中各个参数如表1所示。

Table 1 Ball and plate system parameters table表1 板球系统参数表
进一步通过动力学分析,可得板球系统在x轴和y轴的非线性耦合动力学方程如式(1)和式(2)所示:
(1)
(2)
在实际操作中,式(1)和式(2)中描述的非线性模型难以应用。将其线性化后可得式(3)和式(4),如下所示:
(3)
(4)
3 控制器的设计
3.1 RBF-PID算法原理
RBF神经网络在整定PID参数方面具有自学习和非线性逼近的能力,由此设计的控制器可以实现参数的自适应调整,达到提高板球系统的稳定性和高精度控制的目的。
如图3所示,对板球系统完成解耦后可知x轴与y轴控制原理相同,x方向和y方向的控制器相同,通过库设计控制器以控制x轴、y轴方向的误差,从而使小球能实现沿设定轨迹运动的控制目标。以rin(k)为输入,yout(k)为输出,e(k)为控制误差,ymout(k)为辨识网络的输出,RBF神经网络整定PID的控制结构如图4所示。

Figure 3 Ball and plate system RBF-PID parameter self-tuning control structure图3 板球系统RBF-PID参数自整定控制结构
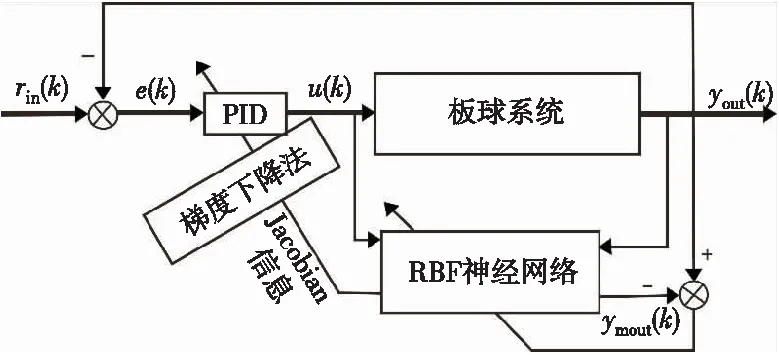
Figure 4 RBF neural network PID control structure图4 RBF神经网络整定PID控制结构
系统控制误差为:
e(k)=rin(k)-yout(k)
(5)
RBF-PID控制器的3个输入为:
(6)
u(k)表示第k次采样时刻PID控制器的输出值,其控制算法为:
u(k)=u(k-1)+Kpxc(1)+
Kixc(2)+Kdxc(3)
(7)

(8)
Kp、Ki、Kd3个参数如式(9)所示:
(9)
在PID参数的在线优化过程中,X=[x1,x2,…,xn]T为网络的输入向量。设RBF神经网络隐含层节点径向基向量H=[h1,h2,…,hj,…,hf]T,其中hj为高斯基函数。第j个节点的中心矢量为Cj=[cj1,cj2,…,cji,…,cjn]T,bj为隐含层节点j的基宽,网络的权向量为W=[w1,w2,…,wj,…,wn]T。∂yout(k)/∂u(k)(Jacobian矩阵信息)通过神经网络辨识得到,第k时刻的∂yout(k)/∂u(k)可以近似等于∂ymout(k)/∂u(k)。
(10)
(11)
3.2 LM_RBF-PID算法原理
针对RBF-PID控制的轨迹跟踪控制实验中系统实时性差且小球震荡大的问题,本文提出使用LM算法代替梯度下降法的同时,引入动量因子的解决方案。LM_RBF整定PID的控制结构如图5所示。
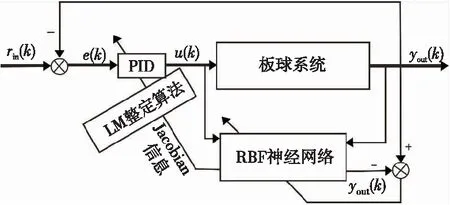
Figure 5 LM_RBF neural network PID control structure diagram图5 LM_RBF神经网络整定PID控制结构
RBF神经网络的参数,在整定过程中均采用梯度下降法来寻找变量的局部极值。针对梯度下降法在实验中稳定性较差且收敛速度慢的问题,在LM算法中引入动量因子α,以达到削弱参数调整中震荡的目的,引入动量因子α后RBF神经网络参数的迭代算法遵循式(12):
(12)
其中,η为学习速率。
动量因子α在参数调节过程中作为阻尼项,确保修正结果沿着参数收敛方向进行调整,算法的收敛速度在很大程度上取决于动量因子α的大小[14]。若α取值过小,收敛速度慢且稳态偏差小,α取值过大,算法产生的稳态偏差较大,故动量因子α的取值对算法的整体控制效果至关重要,α取值与第k次的误差指标E(k)和第k-1次的误差指标的变化量ΔE(k-1)有关:

(13)
LM算法充分应用RBF网络辨识得到的Jacobian信息实现了很好的控制效果。LM算法能有效处理参数的冗余问题,是介于梯度下降法和高斯牛顿法之间的一种非线性寻优算法,非常适用于非线性问题的求解。
用x(k)表示第k次迭代时的参数,第k+1次迭代时新的参数为:
x(k+1)=x(k)-[JT(k)J(k)+μI]-1JT(k)e(k)
(14)
其中,e(k)为控制误差,J为Jacobian矩阵,I表示单位矩阵,μ为大于0的标量。Jacobian 矩阵信息为:
(15)
将上述算法应用到PID控制器的参数整定过程中,PID参数向量K=[Kp,Ki,Kd],则有:
(16)
用LM算法进行优化整定,板球系统中参数向量的变化量为:
(17)
3.3 算法应用步骤
采用LM算法整定PID参数和引入动量因子的LM_RBF-PID控制算法步骤如下所示:
步骤1设置RBF神经网络参数初值bj(0)、cji(0)、wj(0)和隐含层神经元个数f、学习速率η,由式(13)判断决定动量因子α的取值;
步骤2由系统的输入γin(k)和输出yout(k)通过式(6)和式(7)计算u(k);
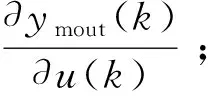
步骤4采用式(9)计算参数Kp(k)、Ki(k)、Kd(k),利用LM_RBF-PID算法整定参数;
步骤5采用误差反向传播法,调整RBF神经网络参数bj(k)、cji(k)、wj(k);
步骤6令k→k+1,重复步骤2~步骤5,直至算法收敛或达到终止条件,完成循环。
4 板球系统控制实验
4.1 板球系统仿真实验
为验证RBF-PID控制算法及其改进算法的控制可行性,设计了RBF-PID控制算法和LM_RBF-PID控制算法的对比仿真实验。分别设置幅值为0.2的阶跃信号和幅值为0.2、频率为0.1 Hz的方波信号,Kp、Ki、Kd的初始值设置为0.02,0,0.5。在Matlab中搭建板球系统的控制仿真模型,二者阶跃响应和方波响应曲线如图6和图7所示。
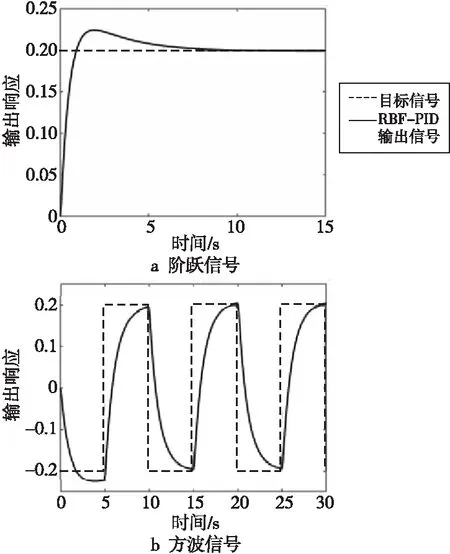
Figure 6 Response curves of step signal and square wave signal of RBF-PID algorithm图6 RBF-PID算法的阶跃信号和方波信号响应曲线
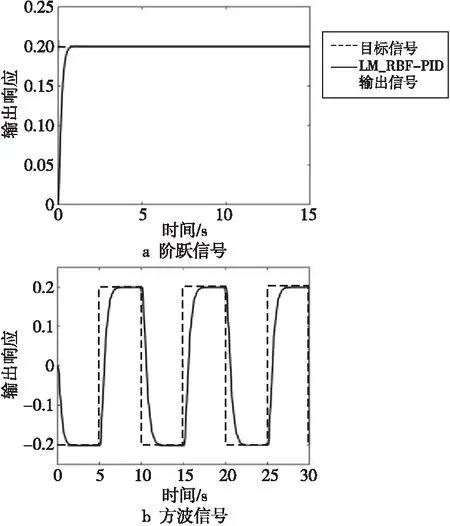
Figure 7 Response curves of step signal and square wave signal of LM_RBF-PID algorithm图7 LM_RBF-PID算法的阶跃信号和方波信号响应曲线
图6和图7中曲线分别为RBF-PID控制算法和LM_RBF-PID控制算法对阶跃信号和方波信号的系统响应曲线。对系统输入阶跃信号,由RBF-PID控制时板球系统的响应曲线可知系统的超调量为12.25%,调节时间为8.3 s;采用LM_RBF-PID控制时板球系统的超调量为0,调节时间为1 s,LM_RBF-PID算法跟踪方波响应的效果也较好。可见,在方波信号作用下RBF-PID控制算法和LM_RBF-PID控制算法均能跟踪方波信号,适用于时变系统的控制,而LM_RBF-PID控制算法的超调量低、响应精度高,控制效果优于RBF-PID控制算法。
4.2 板球系统轨迹跟踪实验
为验证本文改进算法的有效性,以GBP2001板球系统作为实物验证平台,设定以坐标(0,0)为中心、边长为60 mm的正方形目标轨迹,选取多次轨迹跟踪控制实验中控制效果较好的参数值,小球的初始位置坐标设定为(0,0),分别采用RBF-PID控制算法和LM_RBF-PID控制算法在板球系统完成控制时间为30 s的方形轨迹跟踪控制实验。经多次实验对比及整定分析,实验中RBF神经网络的主要参数设置如表2所示。表2中隐含层节点数目设为6,学习速率为0.01,PID的初始参数值设定为Kp=20,Ki=1和Kd=120。选取RBF-PID和LM_RBF-PID控制算法分别完成方形轨迹跟踪的实验。为提高实验准确度和可重复性,实验过程中保持实验平台、小球初始位置、光线等环境不变,实验结果如图8所示。RBF-PID和LM_RBF-PID的方形轨迹跟踪误差对比量化结果如表3所示。其中,振幅5%以上表示小球运动轨迹在63*63(mm)以外。
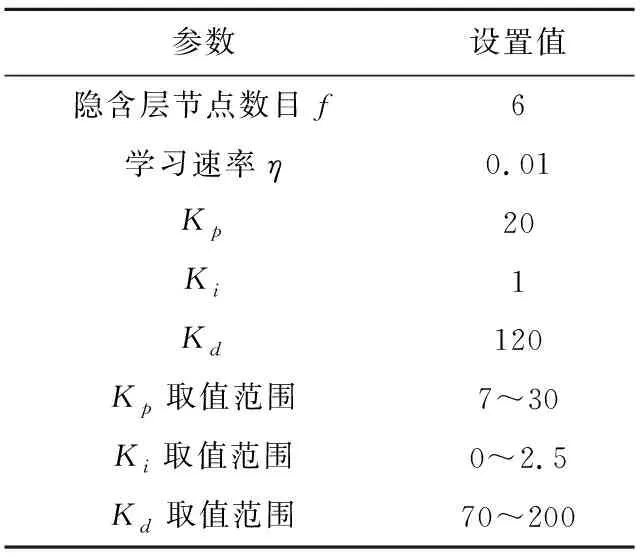
Table 2 Initial value of each control parameter in the experiment表2 实验中各控制参数初始值
由图8可知,小球在球盘上运动过程中,小球的目标位置和小球的运动方向在正方形顶点处会发生较大变化,且小球的惯性会造成响应延迟,导致在小球整段轨迹中4个顶点位置处的轨迹波动较大。在RBF-PID控制过程中轨迹的误差较大,运动曲线不够稳定,对于设定的方形轨迹不能精确复现,如表3所示,其最大震荡位移为68.4 mm,且轨迹振幅>5%的时长为22.8 s。而在LM_RBF-PID控制过程中,小球的最大震荡位移为63.8 mm,运动轨迹振幅>5%的时长也缩短至8.5 s,随着小球运动时间的增加,误差越来越小,轨迹跟踪精度越来越高,能够完成方形轨迹的精确跟踪。
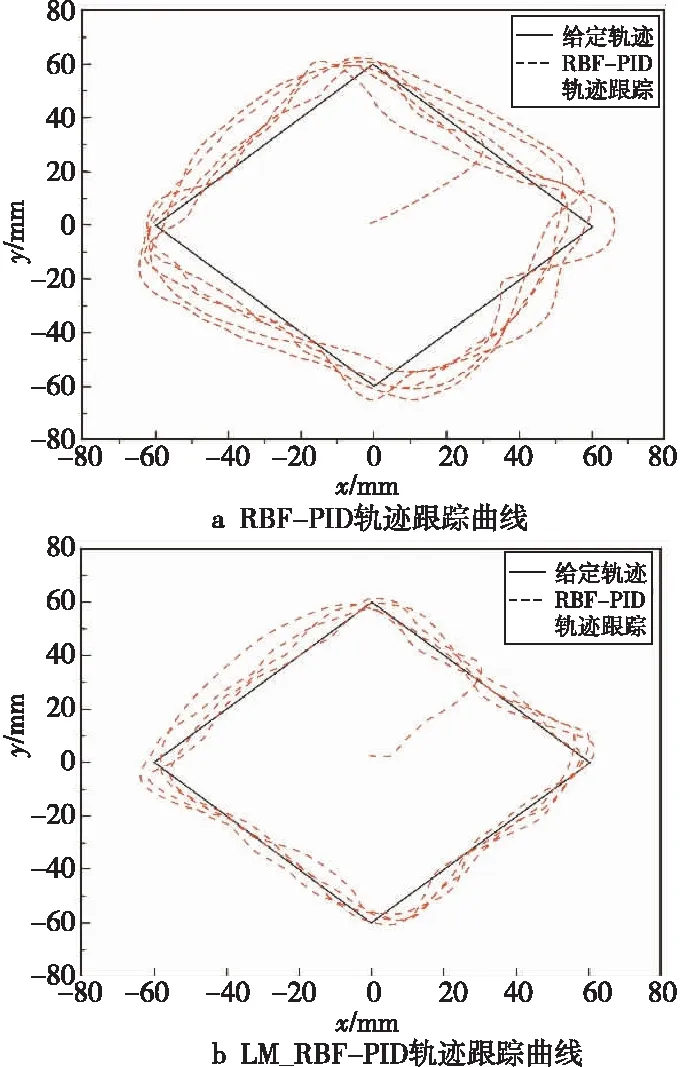
Figure 8 Square trajectory tracking curve of the ball图8 小球方形轨迹跟踪曲线

Table 3 Tracking error comparison of square trajectory表3 方形轨迹跟踪误差对比
5 结束语
本文主要研究了GPB2001非线性板球控制系统,提出用LM算法代替梯度下降法整定PID控制参数,以实现RBF-PID控制的优化,通过在Matlab中的仿真实验,证明了其跟踪非线性时变系统的有效性。通过轨迹跟踪的实验结果可以看出,RBF-PID和LM_RBF-PID控制算法均完成了板球系统的方形轨迹跟踪控制,LM_RBF-PID控制算法在轨迹跟踪实验中,得到的小球轨迹的精确度更高、稳定性更强,控制精度优于RBF-PID控制算法的,能够取得更好的控制效果。

