融合结构与属性视图的可重叠社区发现算法*

昌 阳，马慧芳,2

(1.西北师范大学计算机科学与工程学院，甘肃 兰州 730070;2.广西师范大学广西多源信息挖掘与安全重点实验室，广西 桂林 541004)

1 引言

社区发现算法是发现社区内部结构和组织原则的基本工具，在多个领域发挥着重要作用，如生物网络的新陈代谢网络分析、社交网络中的社区划分等。许多真实世界的网络不仅包含结构信息[1]，节点上还附加了丰富的属性，但仅考虑一类信息源不足以确定社区结构，原因有2个：一是结构通常是稀疏和嘈杂的，若仅使用结构信息来执行聚类，通常会导致不好的划分结果；二是若仅使用属性信息进行聚类，不相关的属性信息也可能会导致非最优的聚类结果。

传统的社区发现算法仅针对结构和属性之一进行挖掘，或是将两者线性叠加再进行挖掘，故不能有效进行信息源的融合[2 - 4]。Whang等人[5]提出的NEO-K-Means(Non-Exhaustive Overlapping K-Means)和Jing等人[6]提出的EWKM(Entropy Weighting K-Means)都是对K-Means的扩展，前者考虑了类簇之间的重叠性和离群点的情况，但未考虑结构和属性信息，后者考虑了子空间和节点属性，未考虑结构信息。与上述不同，部分社区检测算法同时考虑了节点间的属性和结构信息。例如，Yang等人[7]提出的CESNA(Communities from Edge Structure and Node Attributes)算法考虑了2种信息源，但相对重要性无法自动计算；Chen等人[8]提出的TW-K-Means(Two-level variable Weighting K-Means)算法未考虑可重叠的情况；Ruan等人[9]提出的CODICIL(COmmunity Discovery Inferred from Content Information and Link-structure)算法使用属性为每个节点找到最近的邻居，然后通过将每个节点与其相邻点相连来保留图属性信息对图进行重构；Cohn等人[10]以实验方式调整每个信息源的重要性，简单地将所有节点权重固定为特定值。然而，并非所有待聚类的节点的结构和属性信息在决定节点的隶属关系时都具有相同的重要性。此外，作为传统聚类算法在高维空间中的延伸，基于子空间的聚类算法认为每个类簇是由属性子集标识的一组数据，且不同类簇可以用不同属性子集表示。故此，本文设计了一种计算类簇子空间的算法，在算法每轮迭代过程中更新各类簇的属性子空间。通过定义合理的目标函数约束条件对传统的K-Means聚类算法进行修正，从而计算每个类簇中各个维度的权重，使用权重值来标识不同类簇中维度的相对重要性。

综上，本文提出了一种融合结构与属性视图的可重叠社区发现COCD(Combination structure and attribute view for Overlapping Community Detection algorithm)算法,同时考虑了网络中的结构和属性信息，可以自动计算两者的相对重要性以及社区中特定属性的权重并揭示子空间。

2 准备工作

2.1 问题定义

给定属性网络G=(V,E,F)，其中V={v1,v2,…,vn}是n个节点集合；E是边集，且|E|=m；F={f1,f2,…,fr}是r个属性的集合；A表示邻接矩阵，若节点vi和vj间有边，则Aij=1，否则为0。假设将图划分为k个社区，C={c1,c2,…,ck}。表1总结了本文用到的重要符号。

Table 1 Several important mathematical notations表1 本文所用到的符号

2.2 双视图的构建

将图G分别表示为属性视图G1和结构视图G2，其中G1用属性矩阵AF=[fij]∈Rn×r表示，fij为节点vi在第j维上的属性；G2用结构矩阵As=[Bij]∈Rn×d表示，Bij为节点vi在第j维上的结构嵌入值。

2.2.1 属性视图的构建

对于属性图中的每一个节点，它与r维向量表示的属性相关联。每个向量中的元素是节点的属性值。属性值可以是单个单词、标签等，取决于给定网络的上下文。给定数据点矩阵X=[Xij]∈Rn×m，每个数据点上附着各自的属性{f1,f2,…,fr}，由此形成属性矩阵。

2.2.2 结构视图的构建

构建结构视图旨在将信息网络嵌入低维空间，可将每个节点都表示为一个低维向量。经典的图嵌入算法之一如DeepWalk[11]，通过对图随机游走得到一些序列，把序列当句子，利用word2vec就可以得到每一个“词”的向量。node2vec[12]可以看作是对 DeepWalk 的一种更广义的抽象，主要是对DeepWalk的随机游走策略进行了改进，因为普通的随机游走不能很好地保留节点的局部信息，所以node2vec增加了2个参数来对节点邻居加以控制，以获取邻域信息和更复杂的依赖信息。Graph2vec[13]直接对整个图进行嵌入，原理与DeepWalk类似。近期提出的用于随机块模型的不同的隐私邻接谱嵌入算法ASE(Adjacency Spectral Embedding)[14]，通过邻接谱嵌入估计接近于Frobenius范数的潜在位置，并在模拟网络和真实网络中达到与期望参数相当的高精度，来有效地进行图嵌入。LINE(Large-scale Information Network Embedding)[15]作为图嵌入的经典算法，融合了一阶与二阶相似度，可以有效地将大规模网络嵌入到低维向量空间，其适用性广泛，这也是本文选择LINE进行嵌入的原因。

定义1(结构相似度) 节点对(vi,vj)的结构相似度是其邻居网络结构之间的相似度，ui是vi被视为节点时的表示，u′i是vi被视为其他节点特定“上下文”时的表示。若无节点同时和vi与vj连接，则vi和vj的结构相似度是0。结构相似度计算公式如下所示：

(1)

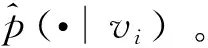
(2)

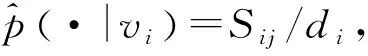
O=-∑(vi,vj)∈ESijlogp(vj|vi)

(3)

与LINE算法[15]类似，通过学习n个节点作为节点的向量表示{ui|i=1,2,…,n}和作为“上下文”的向量表示{u′i|i=1,2,…,n}，使式(3)最小化，能够用d维向量ui表示每个节点vi。

3 COCD算法

3.1 COCD目标函数

现有的基于视图的维度加权聚类算法如TW-K-Means[8]可以执行子空间聚类任务。与在整个数据集的维度上分配权重不同，子空间聚类算法为每个类簇中的每一维度分配权重，因此，不同的类簇具有不同的权重值集合，为了保持可扩展性，在这些新的子空间聚类算法中采用了K-Means 的聚类过程。在每次迭代中，不仅能同时计算视图和维度的权重，还能为视图中的每个维度分配权重。本文融合节点间的属性和结构信息改进了TW-K-Means算法，将固有的子空间聚类算法集成到重叠社区发现的框架中，不仅能自适应地计算2个视图的相对重要性，还能挖掘可重叠的社区及子空间。将数据点X进行预处理后，构建结构视图和属性视图，再聚类为k个簇的过程建模为以下目标函数的最小化：

(4)

其中,U是指示矩阵，表示节点和簇的隶属关系；Z表示簇中心矩阵；w是一个2×1且元素都初始化为1/2的列向量，表示视图的相对重要性；h是m×1的列向量，表示视图下每一维属性的相对重要性。右侧第1项是簇内分散程度的总和，l表示簇编号;i表示节点编号；j表示每一个视图的维度，j=1时表示结构视图，j=2时表示属性视图;t表示视图编号,t=1,2;G1和G2分别是结构视图维度和属性视图维度的集合。第2项和第3项是2个负熵权，λ和η是2个正参数。约束于：

其中,α控制聚类之间的重叠度，0≤α≤(k-1)。算法流程图如图1所示。

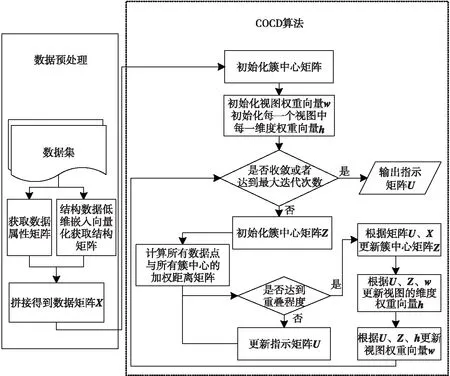
Figure 1 Flowchart of the overlapping community detection algorithm combing structure with attribute view图1 融合结构和属性视图的可重叠社区发现算法流程图

如图1所示，首先，对数据进行预处理后，获取社区发现算法所需的双视图。一方面，从原始属性图上获取属性矩阵；另一方面，利用结构相似度方法将图嵌入到低维空间，转换成低维向量之后得到结构矩阵。由此获得算法需要的原始数据矩阵。其次，随机初始化簇中心矩阵、视图权重以及每一个视图中的每一维权重；再计算数据点与簇中心的加权距离矩阵，根据加权距离矩阵，将数据点分配给距离最近的簇，得到指示矩阵。然后，利用指示矩阵和数据矩阵对每个簇中的数据每一维度求平均值，更新簇中心矩阵。再次，子空间聚类算法为每个类簇中的每一维度分配权重，再更新视图权重向量和视图上属性的维度权重向量，即揭示子空间。最后，计算目标函数的值，查看目标函数值是否收敛，若已收敛，结束算法，得到指示矩阵；若仍未收敛，迭代上述过程，直到目标函数收敛或者达到最大迭代次数，结束算法。此外，目标函数给出了关于算法重叠度的约束条件，使得算法可以检测网络中的重叠社区。

3.2 模型优化

通过迭代求解以下最小化问题来最小化式(4)：

优化目标函数的方法是对U、Z和w以及h进行部分优化。通过迭代算法使得目标函数趋于局部极小值，优化部分每一步都是严格递减的，故算法收敛于局部最小值。对于固定U、Z和h，根据w对目标函数进行最小化时，本文与文献[8]类似使用如下函数更新目标函数。视图权重wt和视图下维度权重hj的计算公式如下所示:

当且仅当给定U、Z和h，下式成立：

(5)

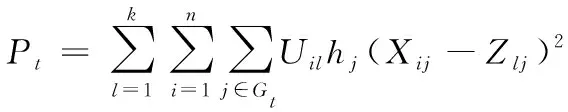
证明对于hj，最小化目标函数式(4)，若j=1，hj表示第1个视图上第j维的重要性，若j=2，hj表示第2个视图上第j维的重要性。对于t=1,2，存在约束∑j∈Gthj=1,0≤hj≤1,t=1,2，通过隔离包含{h1,h2,…,hm}的项,并添加合适的拉格朗日乘数得到形式化后的拉格朗日函数：

η∑j∈Gthjloghj+γt(∑j∈Gthj-1)]

(6)

其中,Qj是在固定U、Z、w时第j维的双视图权重，

对于γt和hj，将L{h1,h2,…,hm}的梯度设置为0，得到：

∂L{h1,h2,…,hm}/∂γt=∑j∈Gthj-1=0

(7)

∂L{h1,h2,…,hm}/∂vj=Qj+η(1+loghj)+γt=0

(8)

由式(8)得到：

hj=exp[(-Qj-γt-η)/η]=

exp[(-Qj-η)/η]exp(-γt/η)

(9)

将式(9)代入式(6)得到：

(10)

故

exp(-γt/η)=1/∑j∈Gtexp[(-Qj-η)/η]

(11)

将式(11)代入式(9)得到：

hj=exp(-Qj/η)/∑m∈Gtexp(-Qm/η)

同上可得：

当且仅当给定U、Z和w，下式成立：

hj=exp(-Qj/η)/∑m∈Gtexp(-Qm/η)

(12)

3.3 COCD算法伪代码

根据上述最小化过程总结COCD算法总结如算法1所示。

算法1COCD算法

Input：数据点矩阵X，簇个数k，控制重叠的参数α，正参数η，λ。

Output：U,Z,h,w。

1.随机选取k个簇中心Z;

2.fort=1to2do

3.wt=1/2;

4.forallj∈Gtdo

5.hj=1/|Gt|;

6.endfor

7.endfor

8.r←0;

9.repeat

10. 计算每一个数据点与所有簇中心的加权距离矩阵[djl]n×k;

11. 初始化全为0指示矩阵U;

12. 初始化T=φ,p=0;

13.whilep<(n+αn)do

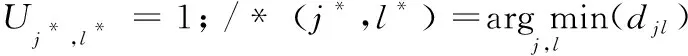
15.endwhile

16. 更新簇中心矩阵Z,根据式(5)更新w,根据式(6)更新h;

17.r←r+1;

18.until目标函数值到达局部最小值或达到迭代次数

在算法1中，X是进行预处理之前的n个数据点矩阵；k是输入簇的个数；α是控制重叠程度的参数，η，λ是2个正参数；T表示存放节点被分配到簇的集合，集合中的元素是节点和簇的二元组，表示该节点被划分到了相应的簇；p是确定重叠度的参数。1～7行是初始化过程，初始化簇中心矩阵Z、视图权重向量w、视图下维度权重向量h。第10行是计算加权距离矩阵。第11、12行初始化一些参数。第13～15行用来判断重叠度是否达到要求，若未达到要求，继续分配数据，否则停止分配，第13行进行(1+α)n次赋值，保证目标函数满足第1个约束条件。第16行更新簇中心矩阵Z、视图权重向量w、视图下维度的权重向量h。第18行判断目标函数是否收敛。

COCD算法涉及到的主要计算步骤有以下3步，运行时复杂度可以分析如下：

(1)划分：将数据分类为k个可重叠的类簇，计算加权距离矩阵，复杂度为O(nk)；再根据加权距离矩阵将数据点进行划分时，时间复杂度为O((n+αn)×nk)，由于α经常比较小，故复杂度为O(n2k)。

(2)更新簇中心：给定指示矩阵U，更新簇中心就是在同一个类簇中找到数据对象的均值。因此，对于k个类簇，这一步的计算复杂度是O(nk(|G1|+|G2|))。

(3)更新视图权重w及视图维度权重h：给定U，Z与h，根据式(5)更新w，只需遍历整个数据集一次来更新h，因此此步骤的复杂度为O(nk(|G1|+|G2|));给定U,Z与w，根据式(5)更新h，同理，只需遍历整个数据集一次来更新h，因此此步骤的复杂度为O(nk(|G1|+|G2|))。

如果聚类过程需要td次迭代才收敛，则该算法的总计算复杂度为max(O(tdnk(|G1|+|G2|)),O(tdn2k))。COCD算法使目标函数值单调下降，直到其收敛到局部最小值。

4 实验

为了全面评估COCD的有效性和效率，本节分别在人工和真实数据集上设计了2组实验。首先描述实验所用数据集；其次观察不同参数值对实验结果的影响，选择适宜的参数；然后分析算法的可扩展性；最后选取4个典型的社区发现算法及未经3.2节优化的本文低阶算法COCD(Naive)与本文算法在人工网络和在真实网络上对比算法性能。

4.1 数据集与评价指标

4.1.1 人工网络数据集

具有基准社区的人工网络是基于LFR基准[17]生成的，其具有与真实世界网络类似的特征。通过设置人工网络的一些重要参数，最终生成了具有5个基准社区结构的人工网络(syn1～syn5),如表2所示。

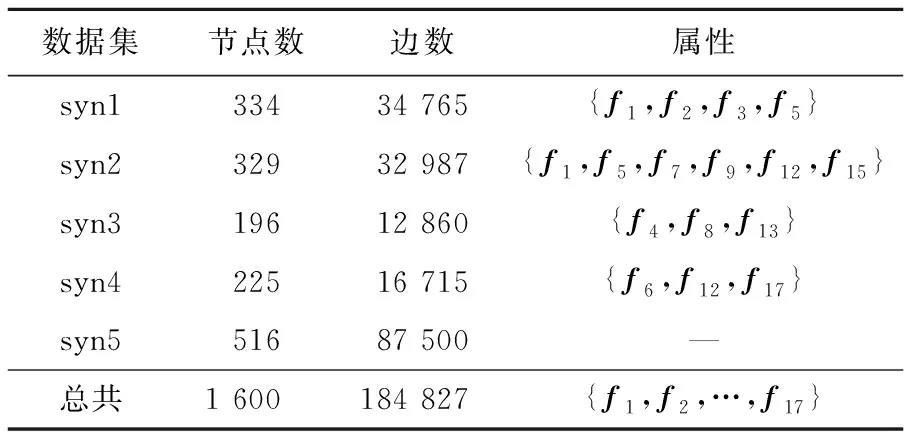
Table 2 Synthetic network datasets表2 人工网络数据集

4.1.2 真实网络数据集

对已有文献中所广泛应用的网络数据集进行了收集和整理，具体有：Flickr数据集[18]是图像共享网络，节点表示用户，边是友谊关系，属性为用户的图像标签，用户有此标签属性给1，否则给0。Amazon数据集来自产品共同购买网络，可从斯坦福大型网络数据集获得，其中节点是产品，共同购买的产品通过边连接，属性为产品具有的特征，每个节点都包含多种类型的属性。Cora是一个论文数据集，本文采用常振超等人[19]的方法，对原始Cora数据集进行精简，去除了在论文中词频统计小于10的单词，其中，边是论文之间的引用关系，至少引用一次，两者之间相互引用均记为一条连接关系，文档所有者之间相互引用均记为一条连接关系，以文档所出现的单词作为文档的节点属性。3个真实网络数据集总结如表3所示。

Table 3 Real network datasets表3 真实网络数据集

4.1.3 评价指标

本文采用与文献[2]和文献[4]中相同的对经典F1分数和NMI(Normalized Mutual Informaiton)分数的改进评价指标平均F1分数和平均NMI分数来进行评估。

4.2 实验结果与分析

4.2.1 参数设置

COCD算法包括3个重要参数α，η和λ，本小节讨论如何在实验中设置这3个重要参数。参数α是直观的，允许指定类簇的重叠程度，参数η和λ可以通过实验来验证其最优值。用户可以用经验知识来估计参数α，如果从经验知识中获取不到，也可以通过使用以下讨论的启发式来估计α值。

图2a和图2b分别显示了COCD算法在5个人工数据集上取不同η和λ值时对聚类结果的影响。由于篇幅限制，且使用NMI分数的量化结果与F1分数的一致，故仅将使用F1分数量化的结果表示出来。从图2能看出，η和λ从0.5变为6的过程中，F1分数的波动不大，即聚类精度对这2个参数不敏感。结果表明COCD算法对参数η和λ具有鲁棒性。

4.2.2 可扩展性分析

通过测量在不断增大规模的人工网络上的运行时间来评估COCD的可扩展性。为了进行评估，考虑6类基线社区检测方法：(1)仅使用网络结构的方法—BIGCLAM(CLuster Affiliation Model for BiG networks)[3]；(2)仅使用节点属性的方法—MAC(Multi-Assignment Clustering)[6]；(3)将两者结合的方法—CESNA[7]；(4)考虑了节点属性以及子空间的算法—EWKM[5]；(5)多视图聚类算法(不能检测重叠社区)—TW-K-Means[8]；(6)未经过3.2节优化的算法—COCD(Naive)。

图3显示了算法的运行时间与网络规模的关系。总的来说，本文算法COCD是最快的算法，一小时左右的时间可以处理约30万个节点；MAC是最慢的，而BIGCLAM比CESNA快，因为它使用与CESNA类似的优化过程，但没有考虑节点属性。对于小型网络(最多17万个节点)，BIGCLAM比COCD(Naive)更快，但是当网络规模变大时，COCD(Naive)会更快。此外，COCD(Naive)是没有经过迭代优化的算法，时间复杂度一般情况下比COCD的小，但对式(4)中带有约束的目标函数进行最小化时，会形成一类非线性优化问题，使得目标函数的解是未知的，所以本文对指示矩阵U、簇中心矩阵Z以及视图的相对重要性向量w和视图下每一维属性的相对重要性h进行部分优化,达到目标函数最小化的目的。最终通过迭代方法使得目标函数趋于局部极小值。故运行时间会比COCD的长。

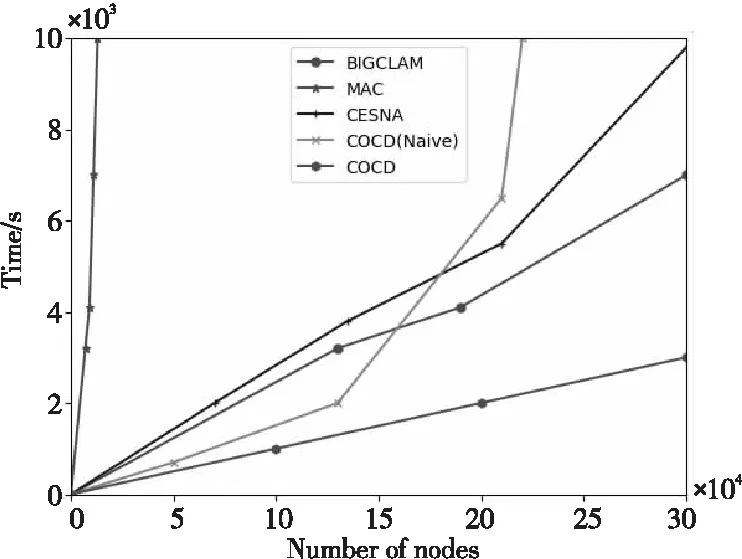
Figure 3 Algorithm running time comparison图3 算法运行时间比较

4.2.3 人工网络和实际网络结果分析

与4.1.1节所提出的对比算法一致，比较本文算法与5个对比算法在5个由LFR基准生成的人工网络数据集和3个真实网络数据集上的平均F1分数与平均NMI值。结果如表4和表5所示。

Table 4 Average F1-scores and average NMI-scores of algorithms on five synthetic datasets表4 5个人工数据集上各算法的平均F1分数与平均NMI分数

Table 5 Average F1-scores and average NMI-scores of algorithms on real datasets表5 真实数据集上各算法的平均F1分数与平均NMI分数

表4显示了人工网络数据集上的实验结果，COCD在10个案例上有8个都得到了最佳的性能。表5显示了在真实网络数据集上的实验结果，将COCD与没有节点属性的BIGCLAM进行比较，注意到COCD得到了更好的性能，因为它结合了来自节点属性和网络的信息。同样，COCD也优于MAC，因为后者只关注节点属性。自然地，COCD绝不会比仅使用单一信息源的最先进算法表现更差。注意到本文基线算法TW-K-Means在人工数据集和真实网络数据集上的表现不如CESNA和COCD，这是因为TW-K-Means在进行社区发现时未考虑重叠度的问题，而真实网络中社区是自然重叠的，故当社区存在重叠情况时检测效果不佳。此外，在将COCD的性能与同时考虑网络结构和节点属性的算法(CESNA)和考虑节点属性以及子空间的算法(EWKM)和COCD(Naive)的性能进行比较时，也能再次观察到COCD的强大性能。

COCD在人工数据集上的NMI值和F1分数优于真实数据集上的值，这是无可厚非的。此外，对于真实网络数据集，COCD在内容共享网络(如Flickr)上相比社交网络上性能增益更佳。例如，在Flickr网络上与除本文算法外性能最佳的算法相比，COCD在平均F1分数和平均NMI分数中分别获得15%和13%的相对增益，可能的解释是，在内容共享网络中，节点的属性(内容)在连接生成中起着更大的作用。总的来说，在16个案例中,COCD在12个案例上性能最佳。

5 结束语

本文提出了一种新的社区发现算法——COCD算法，融合了2种信息源来对属性图进行聚类。该算法可以自适应计算2个视图的相对重要性，并且还为对应视图中的每个维度分配权重以及挖掘子空间。这是一种可扩展的算法，用于大型复杂网络中的重叠社区检测。实验表明，在人工网络数据集和实际网络数据集上，与之前经典的社区发现算法相比，本文提出的COCD算法都显示了较好的性能，提高了社区发现的有效性和高效性。