Mediator的概率扩展*

薛骁勇，孙 猛

(北京大学数学科学学院,北京 100871)

1 引言

在计算机科学和软件工程飞速发展的今天，需要解决的问题的规模越来越大，系统模型和程序实现的复杂程度也越来越高，对整个系统进行直接分析和建模往往十分困难，甚至无法完成。基于组件开发的基本思想是将整个系统分解成多个较为简单的组件，每个组件有特定的结构和功能，对每个组件分别建立模型，最后将各个组件的模型连接起来构成整个系统的模型。它的优点是对组件的建模比较简单，不同的组件可以由不同的团队进行处理，并且组件可被复用于不同的系统之中，从而加速开发过程。

与此同时，对软件安全性的需求也日益增长。但是随着软件系统复杂程度的提高，对安全性的验证往往变得更加困难。为了应对这样的需求，建模语言Mediator[1,2]出现了。它是一门基于组件的形式化建模语言，采用层次化和模块化的基本结构，使用自动机作为最基本的模型单位，对模型进行形式化描述。自动机可以被连接构成系统，从而用于描述更加复杂的系统行为。系统也可以被视为更复杂系统中的组件进行组合，从而形成一种层次化的模块化结构。

与PRISM[3]、UPPAAL[4]等形式化建模工具相比，Mediator不需要使用者有丰富的形式化领域的专业知识，更加方便被学习使用。目前对Mediator也有一些验证和代码生成的工作，例如由Mediator代码自动生成一些程序语言的代码[2,5]，将Mediator模型自动转换到PRISM模型从而能对用Mediator建立的模型进行模型检验[6]。

当前版本的Mediator仅支持对确定性行为的刻画，这已经能描述很多问题了。但是，对于在某些条件下的问题，使用有概率的模型会是一个更好的解决方法，例如对于哲学家用餐问题，就存在不引入其它条件即可解决死锁问题的算法[7]。为了刻画有概率行为的模型，本文对Mediator进行了概率方面的扩展，加入了描述概率行为的语法，并讨论了如何在扩展后的语言中将一个多层的系统展开，转换成单层的自动机。最后通过使用马尔可夫决策过程MDP(Markov Decision Process)定义展开后自动机的语义，给出了展开前多层系统的语义定义。

很多时候仅仅给出模型的描述是不够的，还需要对模型的正确性进行验证。本文通过将Mediator模型自动转换成PRISM模型，可以使用PRISM形式化建模工具中所带有的模型检验器来对Mediator中的模型进行验证。对于扩展前的Mediator模型到PRISM模型转换，已经有了比较完整的工作[6]，在此我们对其进行相应的扩展，使其能够支持扩展后的Mediator语法，从而可以对具有概率行为的Mediator模型进行验证。

本文的正文结构如下：第1节对Mediator进行基本的介绍；第2节给出Mediator描述概率行为的语法扩充；第3节介绍在含有概率的情况下如何将一个多层的系统转变成一个等价的单层自动机，并使用马尔可夫决策过程刻画这个自动机的语义；第4节对PRISM代码的自动生成进行一定的补充，并对一个比特交换协议的具体实例，用Mediator进行建模并将其转换成PRISM模型，使用相应的模型检验器对其进行验证；最后第5节对本文工作进行总结。

2 Mediator介绍

Mediator通过形式化的语法对单个组件进行建模，然后通过各种连接部件将其进行连接。Mediator采用了形式化的卫式转移对组件行为进行描述。一个Mediator程序由类型系统、函数、自动机和系统构成，其定义如下所示：

program ::=(typdef| function| automaton |system)

其中，typedef是Mediator的类型部分，它支持整型、有界整型、浮点数类型、布尔值、字符类型和枚举常量等多种常用的数据类型。而且这些基本的数据类型可以被进一步组合以形成一些更为复杂的数据结构，如多元组、数组、列表等。一个变量在被声明的时候除了必须给出它的数据类型，还可以使用init对其进行初始化。

function是Mediator的函数部分，用来封装一类操作。与一般程序语言中的函数相似的是，它有本地变量，并且通过执行输入变量和本地变量上的操作得到输出变量的值。但它也有不同之处，Mediator中的函数体只包含赋值语句和返回语句，没有其它的控制语句。

自动机automaton是Mediator最基本的组成单位。与一般常见的自动机模型有所不同，在Mediator中自动机没有状态概念，仅仅包含变量声明和卫式转移，这也是为了使Mediator更易于被使用和学习而做出的调整。Mediator中的自动机通过端口与其它自动机或系统进行变量值的传递，端口有输入端口和输出端口2种，输入端口仅能接受外界的消息，输出端口仅能向外界传递消息。一个端口有其本身的类型，以表示它所能传递的变量值的类型。并且端口在创建之时便带有reqRead、reqWrite和value3个变量，前2个用于控制端口的打开或者关闭，最后1个则用来储存传递的值。自动机是Mediator最基本的组成单元，所有行为都要通过自动机来实现，具体的自动机语法规则会在下一节中给出。

system是系统的部分。系统由自动机连接组合而成，系统本身也可以连接组合构成更大的系统，系统部分的语法树如表1所示。

Table 1 Syntax tree of systems in Mediator表1 Mediator中系统的语法树

component和connection是系统最主要的2个部分。component是系统中的组件部分，使用之前定义的自动机或系统对系统中的组件进行描述。connection也使用自动机或系统定义了其所在系统中的一些组件，并且确定系统中组件的端口如何连接。有时系统的构造比较复杂，例如需要将多个自动机发出的消息进行汇总或者将一条消息进行广播，此时可以通过在internal中定义一些节点来使这些关系变得更加清晰。

3 语法扩展

自动机是Mediator语言中最基本的组成部分，是功能的实现。为了扩展Mediator的表达能力，需要对其中自动机的表达能力进行扩展。Mediator中自动机基本的功能和构成已经在第2节进行了基本的介绍，本节给出自动机的组成语法，如表2所示。

Table 2 Syntax tree of automatons in Mediator表2 Mediator中自动机的语法树

一个自动机由端口、变量和卫式转移构成，其中卫式转移是决定自动机行为的最主要部分。一个卫式转移由卫式条件和执行语句构成，当卫式条件被满足时，其所对应的语句便会被执行。执行语句有2类：一类是赋值语句，对自动机的本地变量和端口所对应的变量进行操作；另一类是同步语句，表示在某个端口执行同步操作。如果一个转移包含了和外部端口进行通信的同步语句，则称为外部转移，否则称为本地转移。

在Mediator自动机中，转移是有优先级的。同组转移中排在前面的转移相比后面的转移具有更高的优先级，即只有在前面的所有转移的卫式条件都不被满足且后面转移的卫式条件都被满足时，后面的转移语句才会被执行。如果一个自动机只包含单个卫式转移，则语句的执行顺序就已经被确定下来，这个自动机就是一个确定性的自动机。为了描述非确定的行为，Mediator引入了转移组的概念，即用group来表示一组转移。group后面的大括号里可以包含多个卫式转移语句，一个group内的不同转移之间是没有优先级顺序的，即当有多个转移的卫式条件被同时满足时，将会从这些卫式条件所对应的语句中随机挑选一个执行。与普通转移类似，不同转移组之间也存在优先级顺序，普通的转移可以被看成仅有一个转移的转移组。

上面这种方法虽然可用于描述非确定性行为，但是还不能表示概率行为。为了对概率行为进行描述，本文在之前规则的基础上添加了带有概率的卫式转移，转移的每个分支都带有一个数，代表选择这个分支的概率。扩展后的语法规则如表3所示。其中,prob即为在卫式条件被满足时后面语句被执行的概率。如果在同一条件下有多个转移分支，可以用逗号连接它们对应的多个语句，每个语句都有自己的概率，所有语句的概率相加之和为1。如果一个转移带概率，那么其后面的执行语句只能为赋值语句，即概率转移必定是本地转移。这一设置基本不影响Mediator的表达能力，因为同步语句所在转移的卫式条件大多只涉及端口相关的变量，这样的转移一般与概率无关。

Table 3 Automaton’s syntax in extended Mediator表3 扩展Mediator中自动机的语法

扩展后的自动机可以由一个三元组来表示，即Automaton=〈Port,Variable,Transition〉。Port为端口的集合，Variable是本地变量的集合，transition是带概率的转移组的集合，单个转移被视作只含一个转移的转移组。Variable中也包含2部分，一部分是本地变量，记作vloc，另一部分是端口所涉及的变量，记作vport。

将自动机进行连接组合构成系统这一部分和未扩展的Mediator语言没有区别，仍然按照第2节中系统的语法规则来生成。在这里也用多元组来给出一个系统的表示，System=〈Port,vport,Entity,Internal,Link〉。其中Port是系统和外界交互的端口;vport是端口相关的变量;Entity是大系统中所包含的子系统和自动机的集合，包括所有组件和连接件中的个体;Internal为内部节点的集合;Link是连接的集合，记录了端口、内部节点之间是如何相连的。一个连接形如〈p1,p2〉，其中p1、p2是端口或内部节点，二者必须类型相同，当二者都是端口时，必须一个为输入端口另一个为输出端口。

4 语义扩展

从第3节的扩展语法规则可以看出，扩展后的Mediator语言仍然是一个拥有层次结构的模型。直接为这种结构给出合适的语义定义是比较复杂的，所以本文考虑先将一个多层的系统展开，把它变成一个不具有层次结构的自动机，这样就只需要对一般的自动机确定其语义即可。

4.1 标准自动机

为了将一个系统变为自动机，需要将系统从最底层向上逐层展开，为了方便这种展开，需要引入自动机的标准形式。本文给出标准自动机的定义如下所示：

定义1(标准自动机) 如果一个自动机只含有一个转移组，并且转移组中的每个转移都是标准的，则该自动机被称为标准自动机。

在此定义中用到了标准转移的概念，下面给出它的定义。

定义2(标准转移) 对于一个非概率转移，如果它的执行语句以赋值语句为开始和结束，并且在执行语句中赋值语句和同步语句交错出现，那么它就是一个标准转移。对于一个概率转移，如果它的每个分支的执行语句都满足上述条件，那么它就是一个标准转移。

如果一个系统的组件都是标准自动机，那么在将其转换成自动机的过程中就无需考虑转移的优先级问题，因为每个组件都只有一个转移组。下面给出把一个普通的自动机转换成标准自动机的方法：

首先需要把一般的转移转换成标准转移。对于一个非概率卫式转移g→s1,s2,…,sn，可以用2个操作将其变成标准转移：(1)如果出现连续的赋值语句，可以将其合并为单个赋值语句；(2)如果有2个相邻的同步语句，那么可在其中间插入一个不改变当前所有变量值的赋值语句，例如可将一个变量的值赋给它自己。如果开始和结束的位置上不是赋值语句，那么可以将这样的赋值语句插入到开始或结尾。

不断重复这2个操作，可以将所有的非概率转移转换成标准转移。而对于概率转移，因为其中只有赋值语句而没有同步语句，所以不需要进行这样的转换。

现在只需把同一个自动机的多个转移组合并为一个转移组。考虑一个自动机的转移组如下：

TG1= {g1,1→S1,1,g1,2→S1,2,…,g1,r1→S1,r1}

TG2= {g2,1→S2,1,g2,2→S2,2,…,g2,r2→S2,r2}

⋮

TGn= {gn,1→Sn,1,gn,2→Sn,2,…,gn,rn→Sn,rn}

其中，TG表示的是转移组，优先级高的在前面。因为同一个转移组中的转移没有优先级顺序，所以在这里要做的就是消去各个转移组中的优先级关系。注意到TGi中的转移发生的条件是TG1到TGi-1中所有转移的卫式条件都不满足并且转移本身的卫式条件满足。可以令gi=gi,1∧gi,2∧…∧gi,ri，则转移gi,j→Si,j在合并后的转移组中为g1∧…∧gi-1∧gi,j→Si,j。对原来所有的转移都进行这样的转换之后，即可将所有的转移组合并为一个转移组。上面示例最终得到的转移组为：

TG1= {g1,1→S1,1,g1,2→S1,2,…,g1,r1→S1,r1,

至此已经将一个普通自动机转换成了标准自动机，其中的转移没有优先级关系，这为下一步将系统展开成为自动机提供了便利。

4.2 系统展开成自动机

给定一个系统〈Port,vport,Entity,Internal,Link〉，其所有的子结构都是标准自动机，我们要将这个系统展开成为一个自动机。Mediator中的自动机有3个要素：端口、变量和转移，展开的关键也就是处理这3部分。

端口是与外界进行交互的部分，在系统内部组件进行合并的时候不需要额外的操作，新的自动机的端口就是原来系统的端口。

对于变量，要将原系统各个组件中的变量合并到新的自动机中。对于各个组件的本地变量，为了避免来自不同组件的变量出现变量名重复的情况，需要对变量进行重新命名，在其前面加上其所在自动机的名字。例如自动机A的本地变量state，在展开后的自动机中对应的变量名为A_state。对于内部节点i，添加i_reqRead,i_reqWrite,i_value3个变量到新的自动机中。对于各个组件的端口变量，也需要经过更名后加入到新的自动机中，但区别是可以用Link中的连接减少一些端口变量。若〈p1,p2〉是一个连接，且p1和p2都不是系统的端口时，可以用一个端口替代另一个端口的出现；若二者有一个是系统的端口时，则用该系统端口替代另一个的出现，从而减少变量的数量。

最后考虑转移，转移分为内部转移和外部转移2种。因为每个组件都是标准自动机，它们都只有一个转移组，所以在合并的时候不会涉及到优先级的问题。对于内部转移，因为它们只与其组件的行为有关，所以将变量名替换为更新后的变量名直接加入新自动机即可。由于概率行为只在内部转移中出现，因此对于外部转移的处理和传统的Mediator语言一样[1]，利用依赖图和拓扑排序将所有能够整合的外部转移整合到一起再加入新的自动机即可。

4.3 自动机的语义

对Mediator中的一个自动机Automaton= 〈Port,Variable,Transition〉，本文用马尔可夫决策过程来给出它的语义。马尔可夫决策过程的定义[8]如下所示：

定义3(马尔可夫决策过程) 马尔可夫决策过程是一个四元组〈State,Act,→,s0〉。其中，State是状态集合，Act是动作集合，s0是初始状态，→是转移的集合，它是State×Act×[0,1]×State的一个子集。

Mediator中的自动机没有状态，为了和马尔可夫决策过程的状态相对应，本文通过自动机变量的值来生成状态。用EV(Variable)表示自动机所有变量的所有可能值的集合，其中的一个元素是所有变量的一组可能的取值。这样在自动机所对应的马尔可夫决策过程〈State,Act,→,s0〉中，State=EV(Variable)。初始状态s0即为所有变量取初始值时对应的状态。

动作集合Act= {i}∪P(Port)，用来标记在转移过程中所涉及的端口，其中P(S)表示集合S的幂集；{i}表示转移没有涉及到任何端口，用来刻画内部转移。

转移集合→是State×Act×[0,1]×State的子集。在Mediator的自动机中执行语句只有赋值语句和同步语句2种，而同步语句只标识了哪些端口参与同步，而不改变变量的值，所以只有赋值语句可对变量的值进行修改，即改变马尔可夫决策过程的状态。用s[var→value]表示在状态s下将变量var的值改变成value所得到的新的状态，用a(s)表示状态s在执行赋值语句a之后所达到的状态。转移的规则如图1所示。

Figure 1 Semantics of extended Mediator图1 扩展Mediator的语义

图1中的第1到第3条规则是刻画外部环境对自动机的影响。因为外部环境的变化不可知，随时可能请求读取或写入某个数据，为了能够处理所有可能的情况，其相关的变量可以自由变化。第4条规则是针对外部转移的，因为外部转移不会有概率行为，而且只有赋值语句会改变变量的值，所以仅仅需要将赋值语句作用到现有的状态便可得到新的状态。第5条规则为概率转移对应的语义，因为概率转移不涉及同步语句，所以把所有的赋值语句作用到现有的状态上即可。

5 PRISM代码生成和案例分析

5.1 PRISM代码生成

PRISM是进行概率模型检验时常用的一款软件，被广泛应用于通信协议、安全协议的建模分析等方面。我们希望将Mediator模型转换成PRISM模型，从而对其进行分析检验。PRISM支持使用离散时间马尔可夫链(DTMC)、连续时间马尔可夫链(CTMC)、马尔可夫决策过程(MDP)、概率时间自动机模型进行建模。第4节使用马尔可夫决策过程定义了Mediator的语义，所以在PRISM中的模型也是用马尔可夫决策过程来进行对应。

对不包含概率转移的Mediator模型到PRISM模型的转换，已经有了比较完整的工作[6]。其基本思想是将一个普通的分层的有多个组件的模型转换成一个Mediator中的自动机，然后将这个自动机的变量和转移分别转换成相应的PRISM模型。因为PRISM不支持函数，支持的数据类型也要少于Mediator，为了使转换后的代码能被正确处理，此处考虑的模型中不含有这部分内容。

对于加入概率转移的Mediator模型转换为PRISM模型的方法是类似的，也是先将系统转换成单个自动机，通过上一部分定义的自动机的语义，得到自动机的马尔可夫模型，最后依据这个模型得到对应的PRISM模型。带概率的Mediator模型和原来相比仅多了概率转移，所以在此只需要将其生成对应的PRISM代码。PRISM中转移的形式为[9]：

[]guard→prob1:update1+ … +probn:updaten

其中的update即为对变量进行赋值更新的过程。在系统转换成的自动机中，所有的转移都在同一个转移组中，相互之间没有优先级关系，可以直接将Mediator中的转移对应到PRISM中的转移。

5.2 案例分析

本节使用Mediator描述比特交换协议ABP(Alternating-Bit Protocol)[8]，并将其转换为PRISM代码。在这里考虑的ABP模型结构如图2所示。

Figure 2 Structure of alternating-bit protocol图2 比特交换协议的结构

发信人和收信人通过2个信道进行连接，其中一条为不可信信道，信息在其中可能会丢失，而另一条为可信信道，信息在其中不会丢失。通信开始，发信人通过不可信信道向接收者发送消息，消息中包含1 bit的控制比特(比如本次发送的是0)。如果消息没有丢失，则收信人通过可信信道向发信人将该控制比特发送回去(在此为将0发送回去)。发信人接收到收信人的消息后开始发送下一条消息，该消息中包含和上一条相反的控制比特(这里将1发送出去)。如果信息在不可信信道中丢失了，或者是发信人没有收到收信人的消息，发信人便不断重复发送这条消息，直到收到收信人的消息为止。该系统的Mediator代码如下所示：

system abp () {

components {

sender : Sender;

receiver : Receiver;

}

connections {

Sync(sender.uc,receiver.uc);

Sync(receiver.c,sender.c);

}

}

由于发信人通过不可信信道向收信人进行发信，为了确保收信人能够收到该条信息，让其向收信人不断发信直到收到收信人传回来的消息，同时使用一个变量x来记录发出的控制比特。对于收信人，使用一个变量y来确认是否收到了含有正确控制位的信息，即收信人只接受控制比特和y相同的信息，这用来阻止还没有向发信人反馈控制比特就收到了来自发信人的下一条信息。在这个系统中用了2个可靠的同步信道，其实现在文献[10]中给出了。而不可信信道的特点选择在收信人的组件中进行描述。由此系统生成的PRISM代码如图3所示。

Figure 3 PRISM code generated from ABP model图3 由ABP模型生成的PRISM代码

下面借助PRISM自带的模型检验器对其进行模型检验。因为从发信人到收信人的信道是不可信的，所以用如下规约来确保收信人一定能收到含特定控制比特的信息：

filter(forall,P>=1[Freceiver_z=true],sender_x=true)

这表示对任意满足sender_x=true的状态，最终到达满足receiver_z=true的状态的概率大于或等于1。这表示如果控制比特是1，则其一定能发送到收信人。把上述规约中的true改为false，则规约表示控制比特是0时收信人一定能收到。把二者合并进行检验，结果如图4所示。

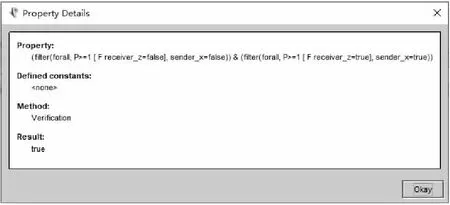
Figure 4 Verification result图4 验证结果

图4显示这条规约是被满足的，这说明通过足够多次的发送，收信人最终一定能收到发信人发出的消息。

6 结束语

Mediator作为一种基于组件的形式化建模语言，其基于组件的特点使得它能够适应更大规模复杂系统的建模工作，并且对模块进行重用能够有效简化建模的过程。本文对Mediator做了概率方面的扩展，使其能够描述含有概率的行为，扩展了Mediator的描述能力。此外还介绍了在扩展之后如何将一个多层的系统转换成没有层次结构的自动机，并且使用马尔可夫决策过程给出了扩展后Mediator的语义。除此之外，本文对原有的Mediator模型到PRISM模型的转换器做了补充，使其能够将含有概率行为的Mediator模型转化成PRISM代码，从而能够对其概率行为相关性质进行验证。