基于改进鲸鱼优化的覆盖表生成算法*
刘向婷,曹小鹏
(西安邮电大学计算机学院,陕西 西安 710121)
1 引言
软件系统的大多故障是由各参数之间的相互作用导致的[1],为了检验这些故障,测试用例的设计显得尤为重要。但是,如果输入参数过多或取值复杂时,测试用例的个数将非常庞大,穷尽测试显得不切实际。在此,组合测试解决了这一难题,它能有效实现各因素取值的充分覆盖,同时能够生成规模较小的覆盖表[2]。
组合测试最小覆盖表生成已证实是一个NP完全问题,为解决该问题,国内外学者研究了多种方法。其主要分为3类[3]:贪心算法、启发式搜索算法和数学方法,其中启发式算法是解决组合测试问题最有效的方法。启发式算法将覆盖表生成问题转化为函数优化问题,即使用遗传算法GA(Genetic Algorithm)、粒子群算法PSO(Particle Swarm Optimization)、模拟退火算法SA(Simulated Annealing)等元启发式算法来实现。但是,启发式搜索算法普遍具有易陷入局部最优的缺陷,表现为收敛精度和收敛速度较低。
本文基于鲸鱼优化算法WOA(Whale Optimization Algorithm)[4]来实现覆盖表生成。WOA是由Mirjalili等[4]在2016年提出的一种新元启发式算法,该算法相比粒子群算法、蚁群算法等,具有参数少、易于实现、收敛速度快和收敛精度高等优点[5]。目前,WOA已广泛应用于图像检索[6]、工程优化[7]、医学[8]等领域,但WOA最初是针对连续问题开发的,其演化过程是在不断更新鲸鱼个体位置而进行的,它不能直接用于解决离散覆盖表生成问题,且对一些复杂优化问题,容易陷入局部最优和出现早熟收敛现象。因此,本文提出一种改进鲸鱼优化的覆盖表生成算法WOACTG(Coverage Table Generation algorithm based on improved Whale Optimization Algorithm)。该算法首先对鲸鱼个体位置进行离散化,并设计合适的适应度函数来更新鲸鱼种群,然后在开发与探索阶段加入演化算子,在此基础上,针对覆盖表生成中算法本身的局限问题,加入平均海明距离和约束处理策略进行优化。该算法用来解决组合测试中覆盖表生成问题,支持变力度和约束模型的处理,以最小化覆盖表的规模为目的,本文给出了相对应的实验,从整体上评估了该算法的性能。

Table 1 Test model of mobile phone camera function表1 手机相机功能测试模型
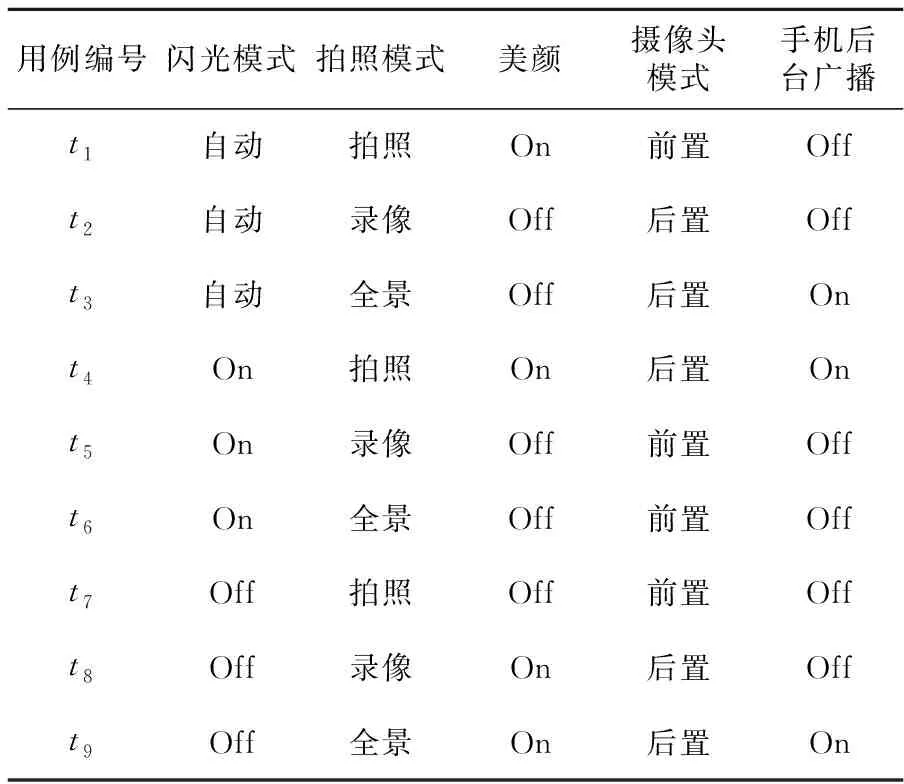
Table 2 2-way coverage table of mobile phone camera function表2 手机相机功能测试2-way覆盖表

Table 3 Added test cases on the basis of table 2 for VSCA(12;2,3223,CA(3,3122))表3 可变强度覆盖表VSCA(12;2,3223,CA(3,3122))在表2基础上补充的测试用例
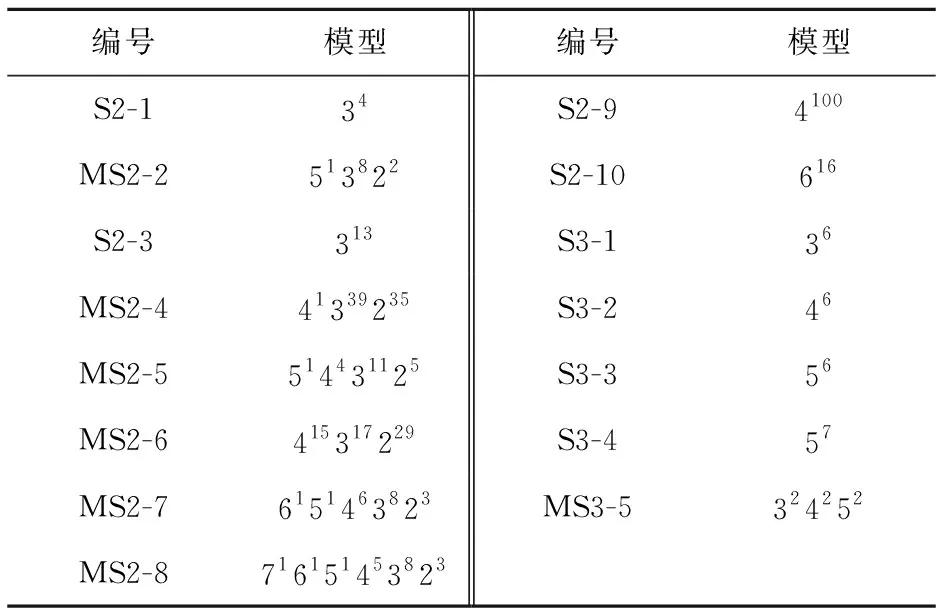
Table 4 Fixed strength instance models without constraints表4 固定力度不带约束实例模型

Table 5 Variable strength instance models without constraints VSCA(2,-,-,CA(-))表5 变力度不带约束实例模型VSCA(2,-,-,CA(-))

Table 6 Fixed strength instance models with constraints表6 固定力度带约束实例模型
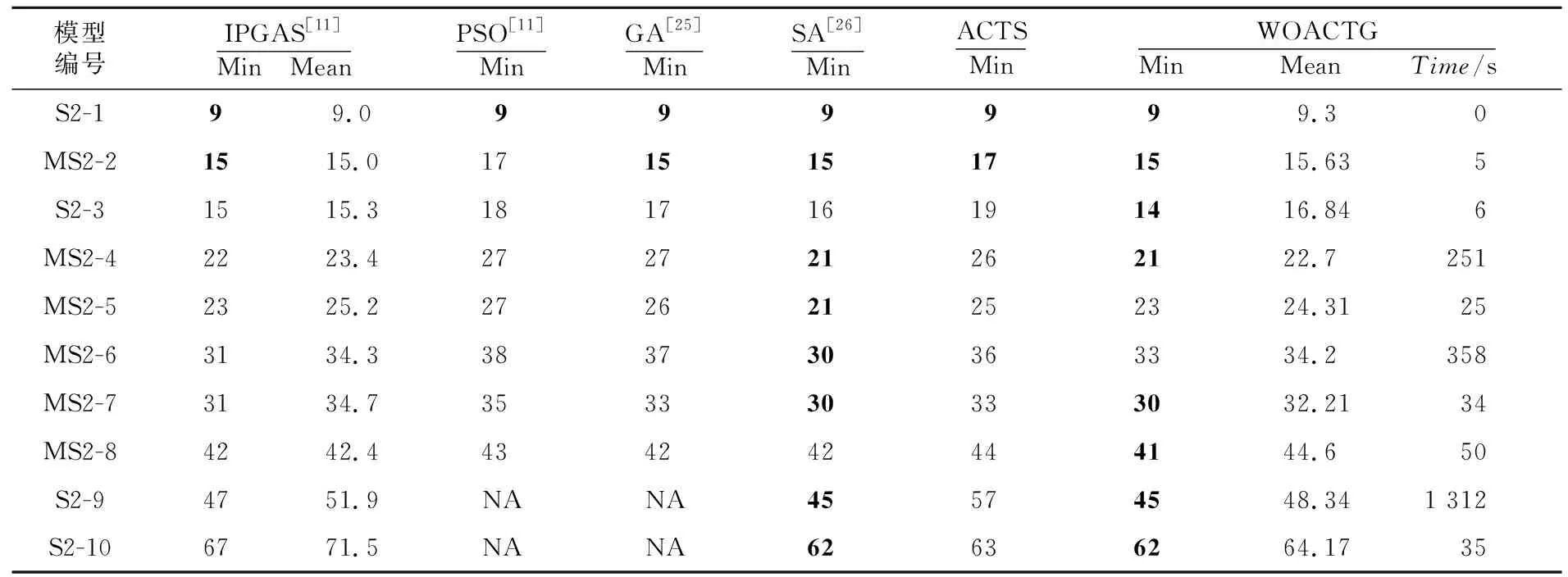
Table 7 Experiment results of 2-way fixed strength表7 2-way固定力度实验结果
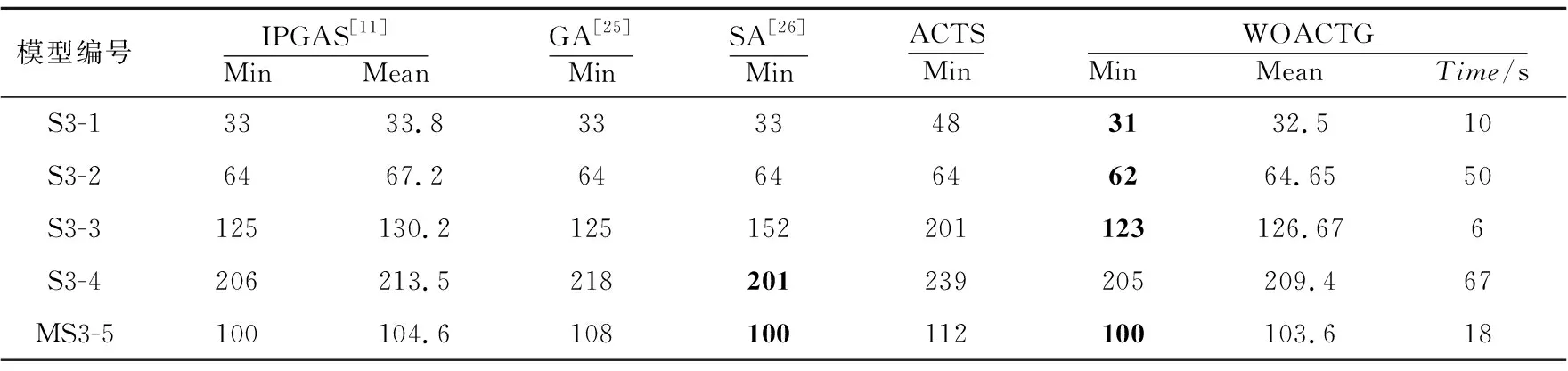
Table 8 Experiment results of 3-way fixed strength表8 3-way固定力度实验结果
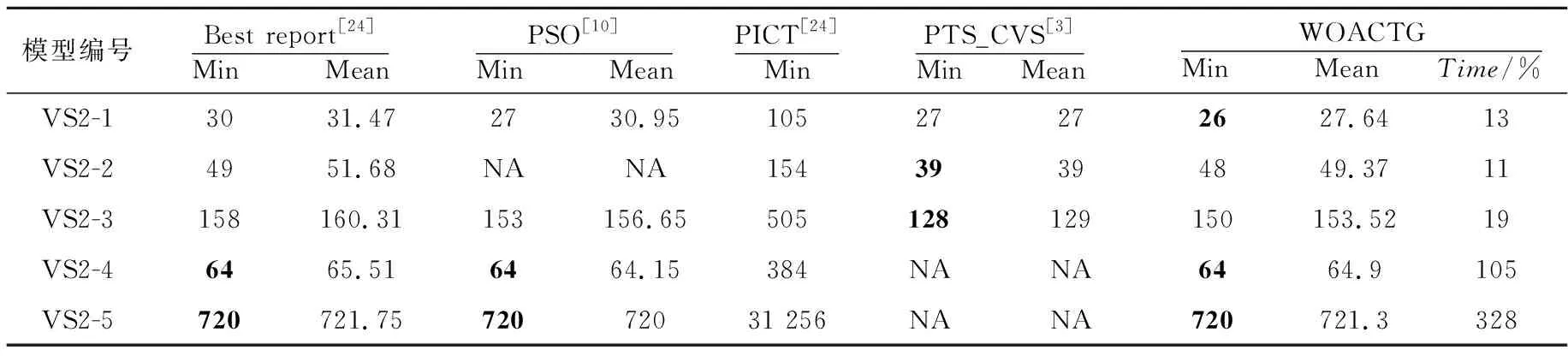
Table 9 Experiment results of 2-way variable strength表9 2-way变力度实验结果

Table 10 Experiment results of fixed strength with constraints表10 固定力度带约束实验结果
2 相关工作
在覆盖表问题上,2012年,时贵英[9]通过分析遗传算法、粒子群算法和蚁群算法的优缺点后,提出了一种新的改进粒子群算法,该算法虽然有效克服了粒子群算法易发生早熟收敛的缺陷,但缺乏对不同算法之间的对比;吴化尧等人[10]在2012年提出了一种适应于覆盖表生成的自适应粒子群算法,且戚荣志等人[11]在2017年基于覆盖表生成问题,提出了一种Spark的岛模型并行化遗传算法,以上2种算法虽然在多组参数取值下生成大多覆盖表均能获得最优结果,但都缺乏对变力度和约束的考虑;2018年,包晓安等人[12]研究了覆盖强度对覆盖表性能的影响,但对粒子群算法易陷入局部最优和后期收敛速度慢的问题没有进行相应考虑。
鲸鱼优化算法最初是针对连续问题而开发的,但目前已被应用于各种离散优化问题中。2019年,Jiang等人[13]用离散鲸鱼优化算法解决绿色车间调度问题,通过实验揭示所提算法在该问题上有很大优势;2019年,Hussien等人[14]对原始WOA进行改进,提出一种二元鲸鱼优化算法,用于处理离散二进制优化问题,将其应用于22个基准函数、3个工程优化问题和1个真实的旅行商问题中,并与5种常见启发式搜索算法进行比较,其准确性和速度均具有明显优势。因此,该算法应用于覆盖表的离散优化问题有很大潜力。
在约束处理问题上主要有3类方法:基于贪婪方法[15]、基于模拟退火的方法[16]和基于SAT求解器的方法[17]。基于贪婪方法虽然提高了测试用例的生成速度,但生成规模相对较大;模拟退火虽然能生成较小规模的覆盖表,但不能保证获得最佳结果。Cohen等人[15]于2008年首次利用可满足性问题(SAT)求解器来处理约束,生成35个含约束的2-way覆盖表;Yu等人[18]在2015年基于禁止元组,提出了约束覆盖表生成,该方法生成的覆盖表规模较大,但生成时间较少;与此不同的是,2015年,Yamada等人[19]使用增量SAT求解器来优化组合测试套件,并验证了相比于贪心算法、模拟退火算法,在生成规模和生成时间上都有优势。
3 背景
3.1 组合测试中的约束
组合测试中的约束是一个重要的研究问题。在实际覆盖表生成中,参数间的相互约束是普遍存在的[20,15],未考虑可能会产生大量无效的测试用例,从而对测试结果的有效性产生影响。例如表1是对手机相机功能的测试模型。该模型共有5个参数,闪光模式和拍照模式分别有3个不同取值,美颜、摄像头模式、手机后台广播分别有2个不同取值。由于录像时音控通道被占用,因此当录像时,手机不可能在后台播放内容,即P2中的录像和P5中的On不能同时取值,意味着(-,录像,-,-,On)将无法实现。同时,现实场景中,参数间的关系紧密程度也不统一,从而存在变力度情况。组合测试通过对参数间的约束进行合理的设计,可以大大提高覆盖表生成的效率。
上述测试模型假设只针对任意2参数间的组合覆盖,则仅需如表2所示的9条测试用例。在所有的测试用例集中,所有的满足约束的2-way组合至少出现一次。例如,对于参数拍照模式和美颜来说,与其相关的3×2=6个2-way组合都在表2中至少出现过一次,同时,所有测试用例都满足相应的约束条件,即(-,录像,-,-,On)不会出现。相关的6个2-way组合为:
(-,拍照,On,-,-),(-,拍照,Off,-,-),(-,录像,On,-,-),(-,录像,Off,-,-),(-,全景,On,-,-),(-,全景,Off,-,-)。
在实际系统中,参数间的作用强度可能不同,对于组合测试,本文用可变强度覆盖表来实现参数间不同组合的覆盖。
假设在上述待测模型中,参数拍照模式、美颜、摄像头模式之间的相互作用较强,我们将此称为可变强度覆盖,其测试用例在表2的基础上增加3条,如表3所示,模型表示为VSCA(12;2,3223,CA(3,3122))。此覆盖表不仅包含5个参数所有的2-way组合,参数拍照模式、美颜、摄像头间的3-way组合3ⅹ22=12也至少出现了一次。
3.2 覆盖表生成框架
组合测试的关键问题是覆盖表的生成,其研究目标是如何生成较小规模的覆盖表。在众多构造覆盖表的方法中,使用最多的策略是One-test-at-a-time[21,22],该策略相应的伪代码如算法1所示:
算法1One-test-at-a-time策略
输入:参数个数n,各参数取值v,覆盖强度τ。
输出:覆盖表T。
1.T=∅;S=the set of validτ-way combinations to be covered;//S等于所有待覆盖的组合对
2.while(S≠∅)do
3.generate a valid test casepto cover the most uncovered combinations;/*调用算法2生成一条适应值最大的测试用例p*/
4.addpintoT,and remove theτ-way combinations that are covered bypfromS/*把p加入T中,并从S中去除p所能覆盖的所有τ组合*/
5.endwhile
6.returnT
在算法1中,通过引入适应度函数来衡量候选覆盖表的质量。这里S表示所有未被覆盖的组合,适应度函数fitness(p)的返回值为测试用例p在S中覆盖的组合数目。
3.3 鲸鱼优化算法
基本鲸鱼优化算法(WOA)模仿了座头鲸的捕食行为,其数学模型包括包围猎物、泡泡网攻击和搜索猎物3部分[4]。为了对这些特征进行建模,用以下公式对搜索代理X的位置进行更新。
3.3.1 开发阶段(包围猎物/泡泡网攻击方法)
(1)包围猎物。
狩猎过程中,座头鲸首先观察猎物的位置并将其包围。在优化问题中,由于初始时最优解是未知的,因此WOA假设当前最佳候选解是目标猎物或接近最优,其他搜索代理寻求在最佳搜索代理的方向上尝试更新他们的位置。其数学模型如式(1)和式(2)所示:
D=|C·X*(t)-X(t)|
(1)
X(t+1)=X*(t)-A·D
(2)
其中,D是当前搜索代理与t迭代时最佳搜索代理之间的长度,t表示当前迭代,X*(t)是到目前为止获得的最佳解,X(t)是位置向量,·表示逐个元素的乘法。在包围猎物时,搜索代理在当前找到的最佳候选解的方向上更新其状态。A和C是系数向量,计算方法如下所示:
A=2a·r-a
(3)
C=2·r
(4)
其中,a是从2到0是线性递减的,r中的元素是[0,1]均匀分布的随机数,A的元素在[-a,a]取随机值。式(2)中搜索代理(即鲸鱼)根据已知最佳解(即猎物)来更新其位置。
(2)螺旋更新机制。
在螺旋更新阶段,搜索代理以螺旋运动的方式向目标移动。数学模型如下所示:
X(t+1)=D′·ebl·cos(2πl)+X*(t)
(5)
D′=|X*(t)-X(t)|
(6)
其中,D′表示鲸鱼和猎物(到目前获得的最佳解)之间的长度,b是定义对数螺旋线形状的常数,l是[-1,1]的随机数。当座头鲸在一个不断收缩的圆环沿着螺旋形路径移动时,WOA实现了2种行为:包围猎物和螺旋更新。为了模拟这2种行为,假设以50%的概率在收缩环绕机制或螺旋模型更新之间进行选择,从而使鲸鱼的位置在此得到优化。数学模型如下所示:
(7)
其中,p是[0,1]的随机数。
3.3.2 勘探阶段(随机搜索猎物)
为了提高WOA的探索能力,引入一种随机搜索代理代替目前最佳搜索代理来更新鲸鱼的位置。当向量的随机值大于1或者小于-1时,选择随机搜索代理实现搜索,以增强算法的全局搜索能力,否则选取当前获得的最佳解实现搜索,即通过式(2)来更新搜索代理的位置。其数学模型表示如下:
D=|C·Xrand(t)-X(t)|
(8)
X(t+1)=Xrand(t)-A·D
(9)
其中,Xrand(t)是从当前种群中随机选择搜索代理的位置而不是选择最优的。
3.4 鲸鱼优化算法生成一条测试用例的流程
算法2给出了WOA生成一条测试用例的过程,该算法可以被算法1调用。在鲸鱼算法生成覆盖表时,将待测系统的参数看作一个d维空间,记鲸鱼个体的位置为Xi(t)=(x1(t),x2(t),…,xd(t)),其表示一条候选测试用例。这里适应值函数用式(10)表示:
fitness(Xi(t))=|Sτ({Xi(t)})-Sτ(T)|
(10)
其中,τ表示覆盖强度,T表示生成的覆盖集,Sτ(T)表示所有τ组合被T所覆盖的个数,取适应值较大的作为最优候选解。
算法2WOA生成一条测试用例的过程
输入:参数个数n,各参数取值v,待覆盖组合S。
输出:测试用例X*(t)。
1.t=0,X*(t)=0;
2.for(每头鲸鱼Xi(t))do
3. 随机初始化位置Xi(t);
4.while(t 5. //适应值评估阶段 6.for(每头鲸鱼Xi(t))do{ 7. 计算鲸鱼适应值fitness(Xi(t)); 8.if(fitness(Xi(t))==C(n,τ))then/*C(n,τ)表示一条测试用例最多覆盖的组合数*/ 9.returnXi(t)}/*种群中适应值最大的作为X*(t)*/ 10. //位置更新阶段 11.for(每头鲸鱼Xi(t))do 12. 更新a,A,C,l和p;//A是一个系数向量 13.if(p<0.5)then 14.if(|A|<1)then 15. 使用式(2)更新鲸鱼的位置; 16.elseif(|A|≥1)then 17. 使用式 (9)更新鲸鱼的位置; 18.endif 19.elseif(p≥0.5)then 20. 使用式 (5)更新鲸鱼的位置; 21.endif; 22.t++; 23.endwhile; 24.returnX*(t) 算法2中,t表示当前迭代,Max_Iteration表示最大迭代次数。 由于鲸鱼算法中的位置是实数值,即应用于覆盖表时必须对位置进行取整,因此需要对算法进一步改进。本文给出2种优化策略,使其能更好地适用于覆盖表生成。 本文基于离散的概念,对鲸鱼位置采用编码转换的思想,提出一种新的位置表示方法。在WOACTG中,用Y表示覆盖表中一个候选解组合,记Y(t)=[y1(t),y2(t),…,yd(t)]∈[0,1,…,n-1]d(n≥2)为所求的一个可行解,其中d表示维度。这里将待测系统的参数看作一个d维空间,每头鲸鱼个体的位置表示一个候选解,记鲸鱼个体的位置为Xi(t)=[x1(t),x2(t),…,xd(t)]∈[-P,P]d,鲸鱼的位置转化函数Y(t)=φ(Xi(t))表示如下: (11) 上述公式将Xi(t)的d维实数空间向量[-P,P]d编码转换为离散向量[0,1,…,n-1]d(n≥2),即分段函数是将[-P,P]d分成n个小区间,然后利用适应值函数来评估可行解Y(t)的大小,最终找到问题的最优解。 其中,P为一正实数,表示所求问题的取值范围,一般P取值随n的增大而增大。在WOACTG中,Y(t)=[y1(t),y2(t),…,yd(t)]∈{0,1}d,即采用个体编码为{0,1}d上的一个d维整型向量来求解,变量yi(t)(0≤i≤n-1)表示项i是否被用于鲸鱼位置的更新,取[-P,P]=[-3.0,3.0]。 对于启发式搜索算法,开发与探索两阶段的平衡对于算法的搜索能力非常重要。基本鲸鱼优化算法中使用系数|A|来平衡两者之间的关系,若|A|≥1时,强调搜索代理远离参考鲸鱼,随机选择搜索代理实现全局搜索;相反,|A|<1使用到目前为止最佳的搜索代理实现位置更新。A的值随α变化,而α是从2到0线性递减的,不能充分展现算法的实际更新方式,因此对算法搜索与开发之间的平衡不能很好地展现。在此引入一迭代演化算子pi∈[0,1],表示选择已有组合中参数进行更新的概率。对于每头鲸鱼个体,在当前代中生成一个随机数rand∈[0,1],如果rand≤pi,则将在开发阶段实现更新,否则,将在探索阶段进行更新。若pi取值较大,在一定程度上能较快实现位置更新,但容易陷入局部最优;相反,探索阶段的取值决定了对鲸鱼个体新位置进行变异的概率,若取值较大,则可以增加种群的多样性,但算法的收敛速度也随之降低。因此,合适的pi选取对于算法性能有很大影响,用如下公式表示pi的值: pi=pimax-(pimax-pimin)×(t/tmax)2 (12) 其中,pi为定义的选择概率算子,pimax和pimin是pi的最大值和最小值,tmax为最大迭代次数。 4.3.1 位置调优 为了衡量当前测试用例与已生成覆盖表之间的紧密程度,本文引入了海明距离的概念,用d12表示2个测试用例c1与c2之间的海明距离,即2个测试用例间取值不同的参数个数。用平均海明距离H(c,T)表示测试用例c与覆盖表T中每条测试用例间海明距离之和的平均值,其表示如下所示: (13) 上式中,WOACTG在适应值最大的候选解与当前测试用例集之间选择一个平均海明距离最小的作为全局最优解,如假设Xi(t)表示一条测试用例,若Xi(t)=(0,0,0,0),则(0,0,1,1)与其平均海明距离为2,而(0,1,1,1)是3,即选择前者作为全局最优解。这样就可以在具有较大适应值的测试用例中,选择海明距离最小的作为最优测试用例,从而为生成更小规模的覆盖表提供可能性。 4.3.2 约束处理 如第3节所述,参数间的约束关系普遍存在,未考虑可能会产生大量无效的测试用例,从而对测试结果造成影响。因此,在覆盖表生成中,约束处理至关重要。本文利用约束求解器法[16]和适应值惩罚项法[23]来避免约束。在初始化种群阶段,使用SAT求解器来判断每头鲸鱼的位置(即测试用例)是否满足约束条件,若不满足,则该鲸鱼个体将不被放入到种群中。然后在适应值函数的评估中加入惩罚项,使可行解的适应值大于不可行解的适应值。适应值函数表示如下: fitness(Xi(t))=|Sτ({Xi(t)})- Sτ(T)|-γ·0.5·C(n,τ) (14) 其中,C为一条测试用例最多覆盖的组合数,当Xi(t)不满足给定约束时,γ=1,否则γ=0。即在对全局最优的更新上,使用满足约束的解去更新,这样可以使覆盖表中所有的测试用例都是约束满足的,从而提高生成覆盖表的效率。 WOACTG算法的核心是利用编码转换方法将鲸鱼位置表示成一个整数子集的结果,然后用适用于覆盖表生成的适应度函数来评估鲸鱼个体的优劣,使其不断向当前最优个体靠近,最后用改进的方法进行更新,找到全局最优解。WOACTG算法流程图如图1所示。 Figure 1 Procedure of WOACTG algorithms图1 WOACTG算法流程图 WOACTG步骤如算法3所示。 算法3WOACTG步骤 输入:参数个数n,各参数取值v,覆盖强度τ。 输出:最优测试用例X*(t)。 步骤1初始化种群N和C(n,τ)个τ组合。选择一群鲸鱼或搜索代理,在变量区间[-P,P]中随机分配一组数值。 步骤2利用Yi(0)=φ(Xi(0)),1≤i≤N计算个体Xi(0)对应的可行解,并根据适应值函数fitness(Xi(0)),寻找当前最佳解。 步骤3迭代更新。该步骤需要一些子程序,下面将对其进行说明: (1)生成[0,1]随机数α,若α≥0.5,利用式(5)更新,否则,生成随机数β,若β≥pi,通过式(9)更新,否则,利用式(2)更新; (2)判断当前种群中每个个体更新是否完成,若完成则利用Y(t+1)=φ(Xi(t+1))计算可行解,并根据适应值函数确定X*(t+1),否则转至步骤(1); 步骤4判断算法是否达到最大迭代次数,若达到,则输出全局最优值,否则跳转至步骤3进行下一次迭代。 实验中,从文献[11]选取了10个2-way和5个3-way的固定力度实例模型,从文献[10,24]分别选取了5个2-way变力度不带约束和固定力度带约束实例模型,分别见表4~表6。 在算法性能比较中,因为有些文献未给出覆盖表生成时间,有的虽然给出,但因为实验环境不同,存在较大差异,因此本实验只对覆盖表的规模进行比较。由于实验的随机性,为使结果更加准确,对每组实验均执行30次求平均,得出覆盖表规模的最小值、平均值及生成时间,时间单位为秒,不足一秒记为0,NA 表示对应值信息没有在已有文献中报告,将每行中的最小规模都加粗表示。ACTS数据通过运行工具生成,由于ACTS的确定性,实验运行1次即可,其他算法没有公开提供的工具,均是与相关文献中公开数据进行对比的。实验中参数设置基于已有文献[4,14]和经验,给出一组建议参数:种群population=100,最大迭代次数Max_Iteration=300,搜索代理数dim=30,参数Pi表示选择已有组合中参数进行更新的概率,Pi取0.3。 实验的软硬件环境为:Intel(R) Core(TM) i5-8250U CPU @1.60 GHz、8.00 GB内存、64位Windows 10,实验中所有代码均使用C++实现。 (1)固定力度不带约束。 首先,基于表1的模型,用WOACTG与已有文献中覆盖表生成算法进行比较,其结果如表7和表8所示。 由表7结果可知,在2-way实例模型中,WOACTG的覆盖表生成规模显著优于PSO、GA、IPGAS 和ACTS算法的,在S2-3和MS2-8中,WOACTG生成覆盖表规模小于SA算法的,其它实例模型中,模拟退火算法生成的规模均等于或小于WOACTG算法的,模拟退火算法的优势主要在于它的搜索策略[16,26]。如何进一步提高鲸鱼优化算法生成最优覆盖表的能力将是以后的研究工作。 由表8可知,在3-way实例模型中,相比IPGAS、GA和ACTS,WOACT能生成更小规模的覆盖表。在S3-4实例中,模拟退火算法表现优于WOACTG,其余实例中,WOACTG生成的覆盖表规模要小于或等于模拟退火算法的。 (2)变力度不带约束。 基于表5的模型,用WOACTG与已有文献中覆盖表生成算法进行比较,其结果如表9所示。 从表9分析可知,WOACTG在生成的覆盖表规模上整体优于其他算法的,除了在VS2-2和VS2-3上大于PTS_CVS外,在其他算法以及模型上都取得了较优值,虽然VS2-4、VS2-5上与PSO或已有文献规模相同,但远小于PICT的。 (3)固定力度带约束。 从表10中可以看出,WOACTG能在60%(3/5)的情况下生成小规模的覆盖表,虽然在CS-1和Concurrency中生成的覆盖表规模略大于已有算法的,但在时间上远小于HHSA-H。 本文基于鲸鱼优化算法提出了一种适用于覆盖表生成的鲸鱼优化算法。该算法根据编码转换思想,实现算法的离散化,从而完成覆盖表的生成;加入海明距离来避免算法陷入局部最优,通过约束求解器和适应值惩罚项的方法,完成了参数之间的约束处理。实验结果表明,该算法与已有IPGAS、PSO、GA、SA、ASCT、PTS_CVS、PICT和HHAS-H算法相比,能生成规模较小的覆盖表,具有较好的性能优势。在下一步的工作中,将研究初始化方法和参数调优来进一步提高算法性能,使覆盖表生成朝着更加高效、自适应的方向发展。4 改进鲸鱼优化的覆盖表生成算法
4.1 鲸鱼优化算法的离散化方法
4.2 迭代演化算子
4.3 优化策略
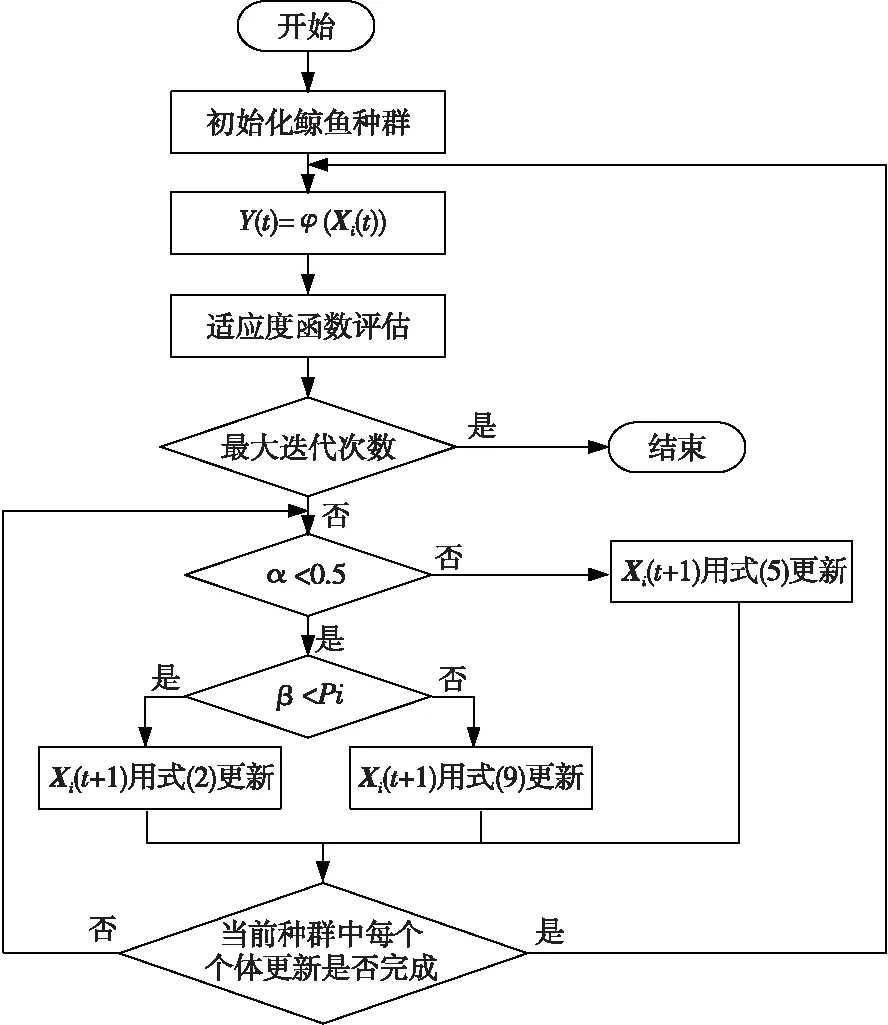
4.4 基于鲸鱼优化的覆盖表生成算法
5 实验
5.1 实验设计
5.2 性能比较
6 结束语

