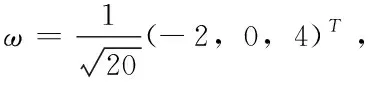基于QR分解的线性方程组Ax=b的最小二乘解
陈 佳 余 苗 陶 婷
(成都理工大学管理科学学院 四川 成都 610059)
如今许多应用问题都需要大规模的科学计算和数据处理,这些问题许多时候直接或间接的需要求解如下线性方程组:
Ax=b
用LU分解比Gauss消去法直接求解节省大量计算。但在许多情况下此方程组没有解,则退而求其次求其最小二乘解。矩阵的QR分解对此有着实际意义的应用。
一、矩阵QR分解的三种方法[1][2][3]
定义1 设A∈Cn×n,如果存在n阶酉矩阵Q和n阶上三角矩阵R,使得A=QR,则称此分解为A的QR分解(或酉三角分解)。当A∈Rn×n时,称为A的正交三角分解。
(一)Gram-Schmidt正交化方法QR分解
定理1 任何实(复)n阶非奇异矩阵可分解为正交(酉)矩阵Q和实(复)的非奇异上三角矩阵R的乘积,且A=QR分解唯一。
证明:存在性 矩阵A的列向量线性无关,写为α1,α2…αn,将其正交规范化为q1,q2…qn。令Q=(q1q2…qn)为正交(酉)矩阵。




(二)Givens变换法QR分解[4]

定理2 任意n阶非奇异矩阵A=(aij)可通过左连乘有限个初等旋转矩阵化为上三角矩阵。

由上可知,A=(Tn-1,n…T12)-1A(n-1),令Q=(Tn-1,n…T12)-1,因旋转矩阵Tij为正交矩阵,所以Q是正交矩阵,R=A(n-1)则A=QR是矩阵A的QR分解。
(三)Householder变换法QR分解
定义3 设单位列向量ω∈Cn,称矩阵:H=I-2ωωH为Householder矩阵,称由Householder矩阵确定的线性变换为Householder变换。
定理3 Householder变换可使任意非零向量ξ变成与给定单位向量γ同方向的向量η

二、基于QR分解的Ax=b最小二乘解[6]
QR分解可用于解线性方程组Ax=b的最小二乘解,设A=QR,则原方程组化为QRx=b,由于Q是正交矩阵,则求上述方程组最小二乘解就是求Rx=QTb的最小二乘解。