企业集团内部信用风险传染效应研究——以某企业集团为例

熊 骁

(重庆工商大学 重庆 400067)

一、引言

进入二十一世纪，全球经济增长速度放缓，实体经济发展出现缩减甚至倒退现象，企业违约事件日益增多，并且关联企业之间还会存在“多米诺骨牌”效应[1-2]。在发展中市场经济体中，企业集团作为弥补资源配置低效的组织形式而广泛存在[4]，在企业集团中，由于各成员企业间的业务关联、资金关联繁多导致子公司之间利益牵扯过甚，成员企业间的信用风险传染的可能性增加[5]。国内外对于信用风险及其传染问题也做了大量的研究，在信用风险度量方面，Naoya，Nobuya[9]和 Kanak Patel，Prodromos Vlamis[6-7]应用KMV模型分别对日本的汽车行业和英国的房地产行业的相关企业所面临的信用风险进行量化分析，他们都发现KMV模型具有较好的信用风险衡量和预测作用；邱鹰，熊桂林[8]通过利用Matlab编程软件对KMV模型进行求解，发现KMV模型对我国上市公司信用风险度量有比较好的适用性。在信用风险的传染问题方面，Bulei Yu[10]等采用灰色综合关联分析方法研究了集团母子公司间信用风险与关联度的相关性，研究表明集团母子公司间关联度与信用风险大致呈正相关；田业钧[12]从信用风险传染的影响因素、传染机制、传染路径等方面进行了分析，对我国信用风险传染现状提出了参考性的防范建议；陈林，周宗放[13]在结构化模型框架下，分析了母子公司间信用风险传递与股权占比之间的联系，发现存在母公司拥有子公司的一个股权比重使得母子公司间的信用风险传递出现最大。目前学者对于信用风险传染问题的研究大多集中在模型的构建与应用上，基于企业集团内部各成员企业间信用风险的尾部相依性来研究企业集团内部各成员企业间信用风险的传染问题的实证研究较少，本文从企业集团内部成员企业间非线性尾部相依关系的角度去刻画风险传染效应，为研究企业信用风险传染问题提供一个新的视角。

本文认为信用风险传染是企业集团内部成员企业信用风险传染通常指的是其内部成员企业间违约概率的相互影响，即某一成员企业的违约概率变化所引起的集团内部其他成员企业违约概率的变化的可能性。由于copula方法对于变量间的非线性相关关系能够进行灵活的刻画，使得copula方法在违约风险相关性领域的应用比较广泛。因此本文首先运用KMV模型构建信用风险的衡量指标，然后从非线性尾部相依关系的角度，运用copula方法对企业集团成员企业间信用风险传染效应的大小进行研究，为企业集团内部信用风险的识别、管理与控制提供依据；同时为商业银行对集团企业内部不同成员企业信用状况的监测，信用异质性企业的识别以及授信决策的做出提供了思路。

二、实证分析

(一)相关样本的选取

样本企业及数据的选取。本文综合数据的可得性、准确性和代表性，本文选取国有控股科技类企业集团中的某重点企业集团作为样本企业集团，分别计算其上市子公司信用风险的大小，为信用风险的传染性的分析提供基础。本文以2013年至2019年作为研究年份，以季度作为时间区间来进行实证分析。一共包含8家上市成员企业的216组信用风险相关性的指标所需要的相关数据，包括股票数据和财务数据。

(二)信用风险度量

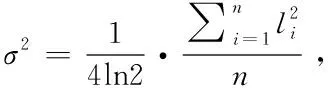
利用MATLAB软件可以计算出VA= 11215，δA= 0.25

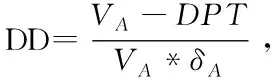
(三)信用风险传染

1.copula函数边缘分布的确定

根据前文的Sklar定理，如果边缘分布函数连续，则可以确定出唯一的copula函数。因此在选择copula函数之前需要确定随机变量的边缘分布函数。常用的确定边缘分布的方法主要有参数法和非参数法，为了能够准确估计两个子企业的违约距离服从的分布特征，本文用非参数法中的核密度估计对两子公司违约距离的分布进行估计。核密度估计方法是根据某一点X周围样本点的稠密来确定X点的概率密度函数值和分布函数值。应用Matlab进行核密度估计，分别得到两公司的核分布估计图如图1图2 所示：

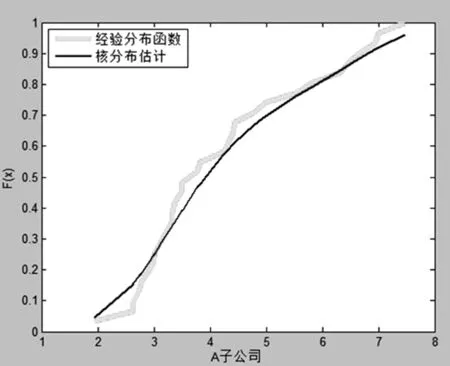
图1 A子公司核分布估计图

图2 B子公司核分布估计图

根据图1和图2所示，图中将核分布估计与经验分布函数进行了对比，发现核估计分布能够很好的拟合变量两公司违约距离DD的边缘分布。

2.copula函数模型的选取

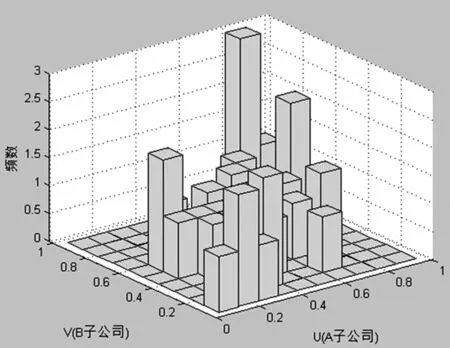
图3 频数直方图

在确定了A子公司违约距离变量DD1和B子公司违约距离变量DD2的边缘分布函数U=F(DD1)和 V=G(DD2)之后，就可以根据(Ui,Vi)(i=1,2,……,n)的分布情况选取恰当的copula 函数，根据频数直方图可以看出：数据多集中在上尾部或下尾部，中部较少，可以确定两者的违约距离在尾部具有更强的传染性，也就是当一个子公司的信用风险增大或者减小时，另一个子公司也会协同运动。为了更准确地描述上述特征，我们来选取合适的copula 函数来描述两个公司的违约距离即信用风险间的传染效应。

不同的copula 函数在描述变量间的关系结构方面具有不同的特点，Gumbel copula 函数和 Clayton copula 函数的分布是不对称的，可以描述两个变量之间非对称的关系。综上所述，为了更加直观的看出不同的copula 函数在描述变量间的关系结构方面具有不同的特点，本文用Matlab软件画出了不同copula 函数的密度函数图和经验分布函数图，如图4-图5所示。

图4 Gumbel copula概率密度函数图

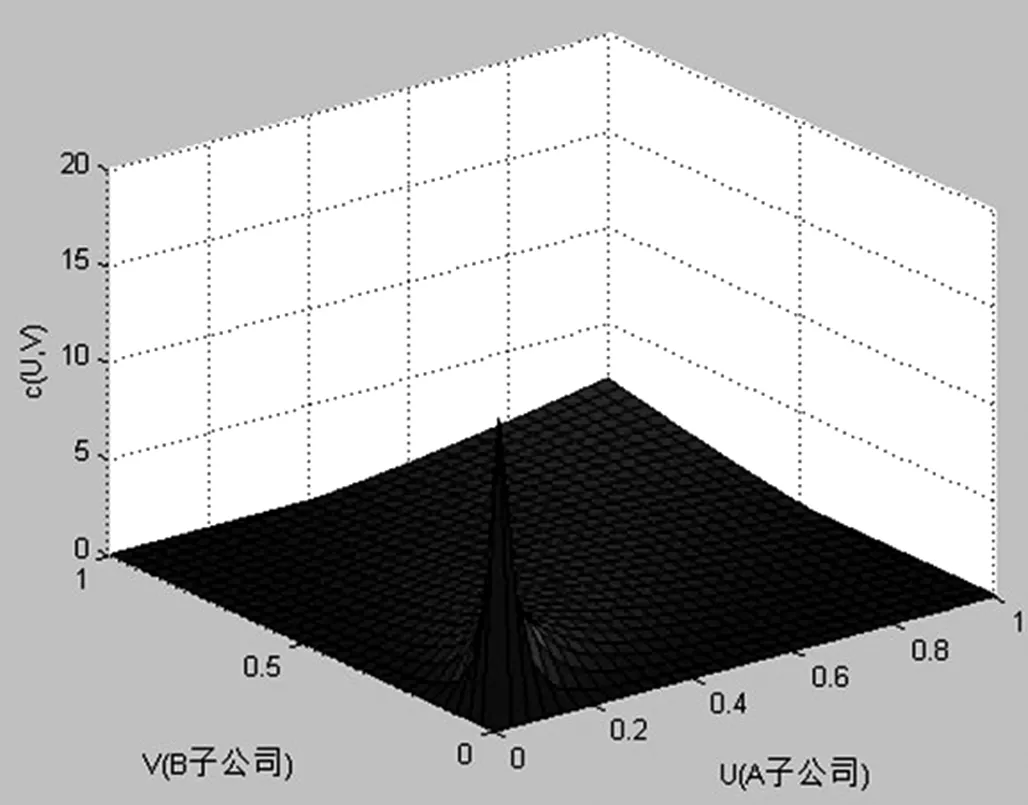
图5 Clayton copula概率密度函数图

根据图4至图5显示，可以更加清楚具体的看出不同的copula 函数在描述变量间的关系结构方面具有不同的特点。针对选取的两个样本企业而言，违约距离存在着较强的尾部关系，而且Gumbel copula函数和Clayton copula函数都分别比较成功的捕捉到了两个变量的上尾部关系和下尾部关系。为了后文更加准确地计算尾部相关系数，进一步度量信用风险的传染概率，分析信用风险的传染效应。本文计算出了不同copula 函数的参数估计结果，其中Clayton copula的参数估计值为2.3406，Gumbel copula为1.8178。

3.尾部相关系数的确定

根据copula理论的相关知识可知，不同copula函数的有关参数与其相关性、一致性的度量往往存在对应关系，利用copula函数参数估计结果和秩相关系数计算结果以及秩相关系数与尾部相关系数之间的关系，可以得出A子企业和B子企业两个样本企业的违约距离的尾部相关系数为λl=0.6830，λu=0.6553。按照上述步骤，可以计算出在95%的置信水平下某企业集团其他子公司两两之间的尾部相关系数，结果如下表所示：

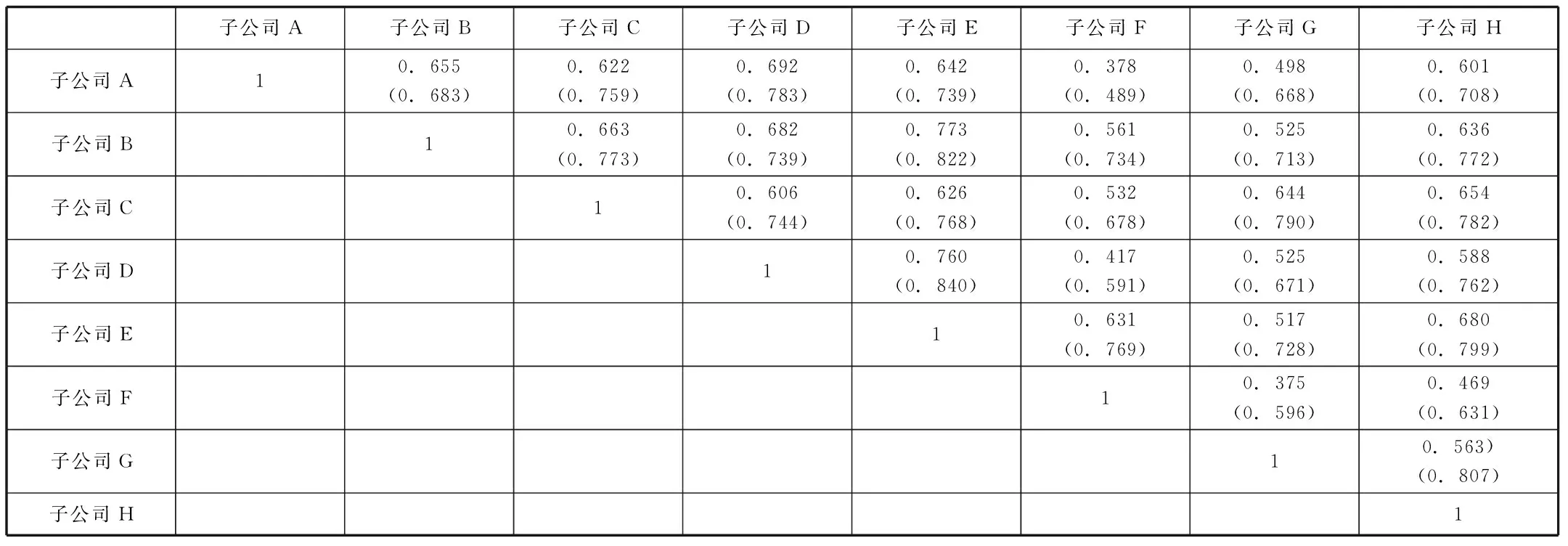
表1 某企业集团子公司间上(下)尾部相关系数矩阵

三、结论与建议

基于上述分析，可以看出企业集团内部的子公司两两之间的信用风险存在着非线性的相关关系，某一成员企业违约距离的变化会引起另一成员企业违约距离的变化，即信用风险在企业集团内部存在着传染效应；尾部相关系数越大说明信用风险的传染效应越强，反之则越弱。根据实证分析的结果，企业集团公司内部两子公司间的尾部相关系数的分布主要集中在0.4至0.88的区间内，说明企业集团某一成员企业违约概率的增大或减小对集团内部另一成员企业违约概率造成同方向变化的可能性集中在40%至88%，两成员公司间存在着较为显著的传染效应；并且从实证结果看，违约距离的下尾相关系数的均值要高于上尾相关系数，说明下尾部的传染效应要高于上尾部的传染效应，即某一成员企业信用风险增大导致另一成员企业信用风险增大的概率大于某一成员企业信用风险减小导致另一成员企业信用风险减小的概率，这就更好地表明了企业信用风险管理的重要性。

由于信用风险传染效应的存在，企业集团在日常的经营管理过程中要及时优化经营管理策略，加快建立信用风险防火墙制度和信用风险预警机制，尽量将信用风险控制在某一成员企业内部，避免通过关联性渠道传递和扩散到其他成员企业。同时，由于信用风险传染效应的存在以及不同成员企业间的尾部相关系数存在着显著的差异，不同成员企业间的信用风险传染效应的大小不同。故商业银行在进行企业集团内部成员企业授信时，可以根据不同成员企业间的信用风险传染效应的大小制定出差别化的信贷政策，重点关注信用风险传染效应较强，影响较大的成员企业，减少金融资产的潜在损失。