James Stewart的微积分教材立体化建设特点及其启示

王海青

James Stewart的微积分教材立体化建设特点及其启示

王海青

（惠州学院 数学与大数据学院，广东 惠州 516007）

为促进教育改革与发展，中国开始在高等教育内部推出“新工科”的高等工程教育教学改革，在基础教育中开展本土化的大学先修课程试点试验．微积分课程是高等工程教育课程体系的基础课程，也是中国大学先修课程试点的主要课程．微积分课程的教材编写与教学方法是改革的重要环节，影响着课程的实施效果．摈弃不同的教育文化背景以及价值理念，剖析美国James Stewart的经典微积分教材编撰特色与成功经验，有助于中国微积分教材的建设与相应教辅资源的开发．

微积分教材；新工科；大学先修课程；教材编写

1 研究背景

为国家战略培养新型人才的需要，教育部在2016年提出新工科概念后，于2017年正式推出“新工科”[1-3]计划．自此，高等工程教育从注重科学研究的“科学范式”转换成为注重实践的“工程范式”．高等教育内部以工程教育新理念、新模式、新方法、新内容、新质量等作为学校新工科建设和教育改革的基本内容．新工科人才培养应该使学生掌握包括自然科学、数学、工程科学、人文社科等方面更先进的知识．因此，新工科的建设和发展也将为其它学科和专业的建设、改革和发展起到引领和示范作用．其中，在高等工程教育课程体系中起着基础和支撑作用的高等数学课程的教学与教材改革也需与时俱进，以符合“新工科”建设的要求．

此外，中国在2000年左右开始探索大学先修课程体系，2013年5月，北京大学成立考试研究院并下设“中国大学先修课程中心”．中国大学先修课程项目（Chinese Advanced Placement，简称CAP）旨在衔接高中教育和大学教育，让学有余力的高中生提前接触大学课程内容，接受大学思维方式、学习方法的训练[4]．首批研发的包括微积分等7门精品课程已于2014年9月起在全国首批试点中学开始授课．有许多研究[5-14]从宏观层面梳理了美国AP课程的理念、价值、内容体系与实施方式及其对中国大学先修课程建设的启示．就大学先修微积分课程而言，它是面向高中生开设的大学数学课程，课程的对象与课程内容的抽象性增加了教材开发的难度．如何开发适合高中生的微积分教材？这也是在后续的教材编写与修订中亟待深入思考的问题．

中美两国的教育目的不同、基础教育与高等教育的课程体系不同、学生的基础不同以及文化背景与价值观也不相同．然而，他山之石可以攻玉．美国成熟的微积分教材体系可以为中国高等数学与大学先修数学课程的建设提供参考和借鉴．

2 James Stewart的微积分教材编撰分析

James Stewart编写的微积分教材堪称经典，在美国微积分教材市场的营销额超过60%[15]，是最受欢迎的微积分教材．James Stewart刚开始编写的微积分教材本是面向高等院校的大学生，随着在高中选修AP微积分的学生越来越多地使用，他对原有的微积分教材不断地进行改善和更新，以满足不同使用者的需要．下面以James Stewart 2014年编写的[16]为例，分析其编写特点，藉此为中国微积分教材与教辅资源的研发带来些许启示．

2.1 人性化的排版方式与细致的学习指导

“微积分入门”简要介绍了促使微积分这门学科产生的面积问题、切线问题与速度问题．数列的极限与数列求和问题，以及解决这些问题的基本思想和方法，主要目的是使学习者对即将要学习的内容及其重要性有一个大致的整体认识，了解微积分与现实的联系．为了说明微积分的广泛应用性和引起学习者的兴趣，教材在“微积分入门”的最后列出了一份包含12个有趣的现实问题清单，这些问题来自教材中的习题或是拓展课题．例如，电影院中最好的座位在哪些位置？飞机要降落，飞行员要在离机场多远的位置开始操作下降？如何解释人观望美丽彩虹时与最高点的视角大概为42°（如图1）？

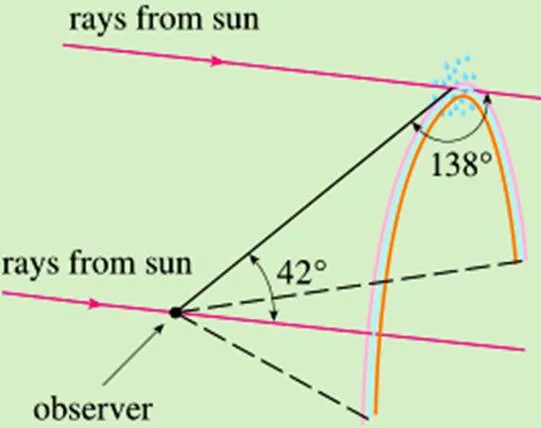
图1 人观望美丽彩虹时与最高点的视角

2.2 数学与人文兼具的内容体系

全书共17章，包含大学微积分的全部内容．分别是函数和模型，极限与导数，导数的运算法则，导数的应用，积分，定积分的应用，积分法的技巧，定积分的更多应用，微分方程，参数方程和极坐标，无穷序列和无穷级数，向量空间和几何空间，向量函数，偏导数，多元函数的积分，向量微积分，二阶微分方程．教材在编写过程中既强调微积分形式逻辑的推导方式，也通过图形、图表等直观形象的描述帮助学生理解抽象的概念和原理．在专注于数学知识的科学性、应用性和思想性的同时，也充分体现了数学与人文的交融．

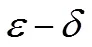
2.3 突出数学教学核心的编写原则

数学课堂教学的核心是揭示数学本质和提高问题解决的能力．数学教学应讲清楚知识的来龙去脉、丰富内涵及其背后的精神实质和思想方法．教师要通过具体知识的教学揭示数学的本质、过程、思想和结构[17]，并让学习者体验到数学来源于现实并应用于现实．“强调对概念的理解”与“提升问题解决能力”是教材的重要编写原则，它来自于1986年以“微积分教学改革运动”为主题的Tulane大学会议[18]．

（1）重视对概念的理解和数学思想方法的形成．

许多概念的形成过程就包含着重要的数学思想方法，微积分概念的思想性尤为突出．“极限”是微积分中最重要的概念，极限思想也是最基本的思想．一系列概念如“连续”“导数”和“积分”都以极限来刻画定义．“导数”和“积分”概念隐含了化变量为常量、化曲为直、化非线性为线性、化全局为局部的极限思想，这也正是微积分的精髓所在．概念的习得一般要经历理解、固化和运用3个环节．James Stewart主要通过“四规则”和设计类型各异的问题促使学习者更好地掌握概念．

图2 割线的斜率

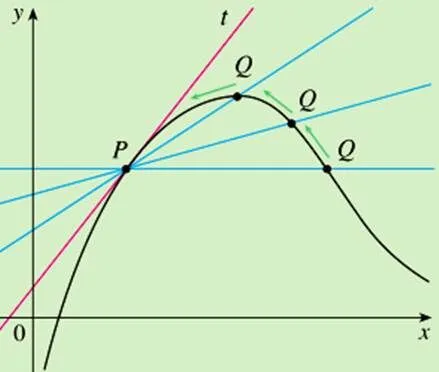
图3 切线的斜率

通过解决某些特定类型的问题有助于概念的固化与运用．教材在每个章节练习题和单元复习题中都设置了大量有针对性的习题，从不同角度、多个层次帮助学习者认识和使用概念．与概念相关的习题主要有4类，分别是：要求解释各章节的基本概念；概念对错判断；通过图形或图表理解概念；利用文字描述并结合图形、数值和代数方法考查对概念的掌握程度．

（2）重视问题解决能力和应用意识的培养．

微积分是继欧氏几何之后数学中最大的发明创造[19]．它的创立首先是为了解决17世纪主要科学问题，如求瞬时速度、曲线的切线、函数的最值及曲线的长度、曲面的面积、曲面围成的体积等．所以，微积分的思想具有广泛的应用性．为此，教材主要通过两种途径来培养学习者的应用意识和问题解决的能力．

一个途径是向读者介绍并运用波利亚的问题解决“四步骤”策略．所谓“四步骤”策略[20]是指：理解题意、拟定方案、执行计划与回顾反思，这一解题策略贯穿教材编写的始终．首先，教材在第一章“函数和模型”的后面专门对“四步骤”策略作了详细介绍，并通过具体例子说明策略的运用．其次，教材在某些原理的推导或证明、例题的解答过程中会在左边的空白处给予解题策略提示．如第一章“函数和模型”1.1节的例题5（如图4，P14），在例题的左边给出了相应的图示及解题提示（如图5）．第三，从第二章到第十六章，每章复习题之后都设置了综合性较高的“附加题”栏目．每个“附加题”栏目都会有一至两道详细的运用“四步骤”策略的例题解答，以便于学习者在剩余的附加题目中仿照学习，并鼓励其用多种方法解决问题．

图4 教材中的例题

图5 教材中的解题提示

另一个途径是让学习者在整个学习过程中不断完成4类不同的拓展课题（应用课题、实验课题、写作课题和探索课题）．从第二章到第十六章，每一章都会穿插一个或多个拓展课题．教材会提供相关的数据、公式、参考资料、大致思路和方向，让学习者尝试着去完成写作任务或利用所学的知识去解决问题．“应用课题”的设置主要是为了激发学习者的想象力，如习题9.3后面的课题：“一个球从初始位置向上抛，它到达最高点所用的时间是否比它从最高点回到初始位置的时间长？”“实验课题”主要涉及到技术的运用，如第10.2节的课题：“如何运用贝塞尔曲线设计激光打印机的字母形状？”“写作课题”需要学习者分析与微积分有关的数学史料并提出参考建议，如第2.7节的课题为“早期求切线的各种方法”．“探索课题”主要是培养学习者的综合运用知识解决问题的能力，如第7.6节的课题是通过对一类不定积分进行“模式识别”归纳出一般结构和解决方法，鼓励学习者参与探索发现．还有其它的一些附加课题则需要在教师的引导下通过团队合作来完成，比如习题5.1的第2题关于“样本点位置的确定”，教师可以指导学习者以小组合作的方式计算数据和绘制草图．

2.4 强调由“特殊到一般”“具体到抽象”的教学方式

图6 矩形的面积

2.5 例题典型且解答详尽 习题难度递进且覆盖全面

图7 参数的解释

James Stewart编写的既是一本可供教师教学参考、学生学习的教材，也是一本容量大、覆盖面广、难易兼顾的习题集．习题包含三大部分：每节知识点对应的课后练习题、每章的复习题及复习题之后的附加题．除个别章节，每节的练习题量超过50道，每章的复习题有100道左右，每章的附加题也有近15道．章节习题的难度遵循“阶梯式”递进的原则，由基础的概念题及简单的计算题、能力提高题和更具挑战性的应用题及证明题几个部分构成．附加题的主要目的是为提高学习者综合运用知识解决问题的能力，引导学习者按照解题策略的步骤理解分析题意、选择方法处理综合性的数学问题与现实问题．

2.6 强大的技术支持与丰富的教辅资源

James Stewart的微积分教材已不仅是传统的纸质教科书，而是依托计算机技术的立体化教学资源库．计算机技术的应用利于学习者直观地理解概念和原理，以及实现探究、验证猜想，降低形式推理的抽象性和学习难度．丰富的教辅资源则满足不同学习者的需要，拓宽教材内容和探究边界．完善的网上作业系统则方便学习者的学习与解放教师．

（1）重视图形计算器和计算机代数系统的使用．

（2）内容丰富的网上同步教辅资源．

图8 章节后问题

图9 穷竭法

TEC中还有一个栏目称为“作业提示”（homework hints）．教材各个章节比较有代表性的习题会用红色字体标出，通常是奇数号，如图8的第33题．这表明此类习题可以通过TEC的“作业提示”来解决．相应的提示并不是具体的解答过程，通常以启发式提问的方式出现，如果前面的提示不能帮助解决问题，则可以进入下一个提示．

（3）灵活的线上作业系统．

James Stewart充分利用网络和媒介，开发和完善网上作业系统，第八版的教材每章习题的70%已经可以通过在线作业系统来完成和批改．这对大班教学的教师来说是体力和脑力的双重解放，大大节省了批改作业的时间，学生也能从中获得及时的反馈．在线作业的使用比例正不断提高，它的吸引力在于易于使用、精准分级和可靠，提高教学和学习的效率．这个系统还包含一些详细的样例，通过链接教材内容和视频一步步地指导学生解决问题．

3 James Stewart的微积分教材立体化建设的启示

国内高校经典的微积分教材编写更多地反映内容的精确、严谨、逻辑性强等特点．由扈志明主编专门为高中学生量身定制的中国大学先修课程教材《微积分》[21]则在坚持传统的基础上，充分考虑到中学生的数学基础与认知能力，编写过程尽可能减少抽象符号语言的描述以体现微积分概念直观与朴素的一面，并且在习题的设置上也做了精心选取，配备了一些设问灵活的开放性题目以满足不同潜质学生的发展需要．但就高中学生群体而言，教材内容直观呈现的程度与方式仍有进一步改善的空间，便于不同学习者使用的配套教辅资源还有待开发．

James Stewart的微积分教材当然也有其自身的缺陷．如在算法算理的教学中难于平衡计算机技术的使用比例，容易造成忽视代数运算技巧而过于依赖技术的情形．此外，教材在许多原理的证明过程中为强调直观阐释而弱化了逻辑的演绎与推导，一定程度上削弱了内容的严谨性．但James Stewart的微积分教材极高的市场占有率也充分说明了教材编写的成功．它具有通俗易懂、直观有趣、强化概念与原理、突出应用等特点，配套的教学辅助资源丰富多样且考虑不同程度学习者的需要．中国微积分教材的编写及其立体化建设应从中借鉴经验．

3.1 配备线上线下交融的教学资源以改善学习者学习体验

随着信息技术的快速发展与更新，人们的学习方式、微积分课程的内容及教学方式也正在发生改变．教材立体化的理念正被教育工作者们广泛接受，教材已经由单一的纸介形式向形式多样的多媒体产品过渡．James Stewart的微积分能成为国际上最畅销的教材与其丰富的多媒体教学资源有很大关系．它的立体化教学资源在多媒体设计与网络教学资源管理等方面都值得借鉴．James Stewart花了大量时间根据用户的需要不断充实、完善和更新网上同步教学资源，使之成为学习者真正意义上的“第二导师”，在课下给予全方位的、人性化的指导．与传统的单纯依靠纸质教材的枯燥晦涩的学习不同，同步学习网站上的课件与资料链接，TEC中的“可视化教具和知识模块”及“作业提示”，精准分级、及时指导与反馈的“作业系统”都给予学习者新的学习体验，便于自学和自我提升．这些完善和丰富的线上线下交融的教学资源对在高中选修AP微积分课程的学生来说尤为重要．

3.2 借助计算机技术降低学习难度拓宽广度和深度

教材通过图形计算器与计算机代数系统的使用，在一定程度上降低了微积分形式推理的难度．但对于技术的使用James Stewart强调不能用计算器代替技能学习或者问题解决，避免学习者滥用技术．相应地，教材的课后习题也专门开辟有允许和不允许使用计算器的题目．

学习者之间的数学基础和自我提升的要求存在差异，James Stewart的微积分课程网站上丰富的操作性强的多媒体资源考虑到了不同学习者的差异性，拓宽了学习的广度和深度．比如网站上提供了大量的提升数学基础的材料或链接，TEC中可供深入探索的“可视化教具和知识模块”、由浅入深启发学生思考的“作业提示”、层级分明与指导有度的“作业系统”、图形计算器与计算机代数系统相关数学软件的使用指导等，既满足了不同学习者的需要，也有效地服务于教师的教学．

3.3 注重通过数学思想方法和文化的渗透揭示数学的本质

微积分课程主要是为了发展学生们对微积分概念的理解，为学生提供微积分方法以及应用这些方法的经验．这反映了数学教学应揭示蕴含在具体知识之上的数学思想、精神与价值，即数学本质．James Stewart的微积分教材重视概念的生成、数学思想的揭示与问题解决能力的培养．如利用“四规则”和丰富的习题加强学习者对数学概念的理解、固化和运用，融合数学史与人文材料体现数学的思想与精神，通过不间断的“解题策略”与“拓展课题”训练提升学习者应用意识、数学建模与问题解决能力．这些方式与途径能大大促进学习者对数学内容的深入认识．

3.4 遵循学习心理与认知规律以促进学习者的理解与掌握

微积分的概念与原理在语言描述上具有高度的抽象性，也体现了数学学科“严谨性”的特点，这给微积分的初学者带来极大的困难与挑战．然而微积分的历史发展表明，微积分的基础是一个逐步严谨化的过程，这门学科产生之初逻辑基础并不严谨．为了突破学习者的学习障碍，James Stewart充分遵循了学习心理与认知规律，在教材编写中贯彻数学教学的基本原则——重视呈现知识的生成与发展过程．他通过“四规则”的方式呈现微积分概念的形成过程，运用“特殊到一般”“具体到抽象”的方式展开微积分原理或规则的证明．具体、直观与形象的描述方式降低了逻辑的严谨性要求，但也保持了适度的形式推理过程，有助于促进学习者对微积分知识的真正理解和运用．

[1] 林健．面向未来的中国新工科建设[J]．清华大学教育研究，2017，32（2）：26-35．

[2] 钟登华．新工科建设的内涵与行动[J]．高等工程教育研究，2017（3）：1-6．

[3] 顾佩华．新工科与新范式：概念、框架和实施路径[J]．高等工程教育研究，2017（6）：1-13．

[4] 中国教育学会．中国大学先修课程项目介绍[EB/OL]．（2016-05-11）[2018-09-10]．http://www.csecap.com/About CAP.aspx.

[5] 罗祖兵，陈方．高中开设大学先修课程的困境与对策[J]．课程·教材·教法，2014，34（9）：97-102．

[6] 杨明全．普通高中开设大学先修课程：理念、价值及实践路径[J]．课程·教材·教法，2014，34（9）：91-96．

[7] 王振存，林宁．美国大学先修课程的理念、优势、局限及启示[J]．课程·教材·教法，2016，36（9）：114-120．

[8] 史宁中．中国大学先修课程研制：理念与作用[J]．数学教育学报，2017，26（3）：4．

[9] 李杨映雪．中美比较视角下的中国大学先修课程及其特色[J]．数学教育学报，2017，26（3）：10-14．

[10] 侯自新．中国大学先修课程的建设与实施[J]．数学教育学报，2017，26（3）：2-3．

[11] 王尚志，胡凤娟．大学数学先修课与优秀高中学生的发展[J]．数学教育学报，2017，26（3）：5-9．

[12] 马峰．基于实践的高中微积分课程比较研究[J]．数学教育学报，2011，20（6）：59-63．

[13] 王海青，汤志娜．大学先修课程背景下美国AP微积分教材的编写特色与启示[J]．数学教育学报，2018，27（2）：74-77．

[14] 秦春华．如何定位中国大学先修课程[N]．光明日报，2014-12-02（13）．

[15] 胡建德．从Stewart的Calculus看高等数学教学[J]．大学数学，2006，22（3）：22-24．

[16]  JAMES STEWART. Calculus [M]. 8th ed. Boston: Brooks Cole, 2014: 1.

[17] 李祎．高水平数学教学到底该教什么[J]．数学教育学报，2014，23（6）：31-35．

[18] 柴俊，张晶．美国的微积分教学：1940—2004[J]．高等数学研究，2005，8（3）：6-116．

[19] 莫里斯·克莱因．古今数学思想（第二册）[M]．上海：上海科学技术出版社，2014：1．

[20] 波利亚．怎样解题[M]．上海：上海科技教育出版社，2007：1．

[21] 扈志明．微积分（中国大学先修课程）[M]．北京：高等教育出版社，2016：1．

The Characteristics and Enlightenments of James Stewart’s Calculus Textbook

WANG Hai-qing

(School of Mathematics & Big Data, Huizhou University, Guangdong Huizhou 516007, China)

To promote educational reform and development, a teaching reform based on the “new engineering program” was introduced in higher education and a pilot study was conducted to localize calculus curriculum in high school. Because calculus is a fundamental course required for advanced engineering education and is also the main high school course for college credits, curriculum and instruction for calculus are an important part of this reform and have an important effect on its implementation. Thus, it would be helpful for developing calculus textbooks in China by analyzing the characteristics of and successful experience using James Stewart’s Calculus textbook.

calculus textbook; new engineering education program; advanced program; textbook compilation

G622.4

A

1004–9894（2020）04–0079–06

王海青．James Stewart的微积分教材立体化建设特点及其启示[J]．数学教育学报，2020，29（4）：79-84．

2020–02–27

广东省本科高校高等教育教学改革项目——基于新工科应用型人才培养的地方本科院校高等数学课程教学改革与实践（2017）；广东省学校德育科研项目（高校思想政治工作课题）——基于“立德树人”的高校课程育人途径探索（2019GXSZ055）；中国教育学会教育科研专项课题——中美大学先修课程数学教材的比较研究（18XM1926015ZB）；惠州学院2017年校级教学成果培育项目——新工科背景下的高等数学教学改革与实践（CGPY2017004）

王海青（1978—），女，广东河源人，副教授，主要从事数学史与数学课堂教学研究．

[责任编校：陈汉君、陈隽]