除数或分母为零时的概述之商榷

常秀芳

（山西大同大学数学与统计学院，山西大同 037007）

清晰、准确、无误的数学概念不仅有助于理解问题时不会发生歧异，而且还体现在数学推理中具有严密的逻辑性、条理性、精确性和简洁性，更会促使问题解决时善于创新[1-3]。

1 除法的定义

定义1已知两个数a、b，如果存在一个数q，使得q与b的乘积等于a，即bq=a，那么这种运算叫做除法。记作

a÷b=q,

读作“a除以b(或b除a)等于q”，数a叫做被除数，数b叫做除数，数q叫做数a与b的商，符号“÷”叫做除号[2]。

2 除法运算的封闭性

从定义即可知道，如果bq=a，则a÷b=q，那么在这种运算关系中，很明确地说明了除法是乘法的逆运算，也就是已知积与一个因数求另一个因数的运算。

2.1 商的存在性

当除数不为零时，商是唯一存在的。

特别地，当除数为零时，因为除数为零，即b=0 时，那么

①当被除数a≠0 时，由于任何数乘以0 都不可能等于数a，所以a÷0 的商是不存在的；

②当被除数a=0 时，因为任何数乘以0都等于0，所以a÷b的商是不确定的，可以为任何的数。

2.2 商的唯一性

数的四则运算，每一个学生都能够掌握，而在没有学习负数时，我们知道，中小学在减法运算中规定被减数不小于减数。这样，加法、减法与乘法运算是封闭，和、差(如果存在)与积都是唯一的。但在除法中为了排除商(如果存在)不是唯一或不存在的情况，于是也需规定在除法中，除数不能是零即可。

在整数范围内，除法运算不封闭，其也不总是可以施行。例如，就不存在一个与2 相乘等于7 的整数，这说明整数集对于除法运算是不封闭的。但是，如果两个数有整数的商存在，那么这个商一定是唯一的。

定理1在除法运算中，若有整商存在，那么商唯一。即若a÷b=q，则商q是唯一的。

证明假设a÷b的商不唯一，有两个不同的商q和q′，即q≠q′，

由除法的定义知

bq′=a，bq=a，

因此0=a-a=bq-bq′=b(q-q′)，

而b≠0，故q-q′=0 即q=q′，这与假设产生了矛盾。所以a÷b的商不能有两个不同的商，于是a÷b的商是唯一的。

3 分数与除法联系

3.1 分数的定义

定义2形如的数叫做分数，其中n是大于1的自然数，叫做分母；m是大于1的自然数，叫做分子；中间的横线叫做分数线[2]。

3.2 分数与除法的关系

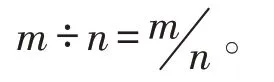
分子相当于被除数，分母相当于除数，分数线相当于除号，分数值相当于商。在除法中，除数不能为零，在分数里分母也不能为零。

分数与除法是有区别的，分数是一个数，除法是一种运算。

4 除数或分母为零是有意义的

在空间解析几何中，方程

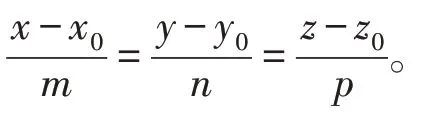
若有一个为0，不妨m=0，而n、p≠0时，方程为

则该直线是平行于坐标平面oyz。

若有两个为0，不妨m=0，n=0，而p≠0时，方程为

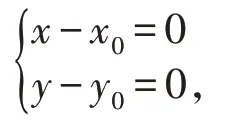
则该直线是平行于坐标轴z轴。

此时分母为零，应用了除法概念中除数为0，被除数也为0，商存在的特性，从而分数值存在。

综上可知，分母为零并不是没有意义。

5 除数或分母为零概述的商榷

在中小学，除法中，当除数为零时，或在分数中遇到分母为零时，它和减法中被减数要不小于减数一样，便于中小学生的认知，应该给学生灌输的是我们暂时不考虑这种情况，也可以说现在我们规定的除数或分母不为零，我相信学生一定能够接受的。

然而，学生在中小学阶段的一些教材教参中，甚至绝大部分教师都认为除法或分数中除数与分母为0是没有意义的。这样使学生经过十几年来定势的影响，到后续的学习造成很大的干扰。本人认为商不唯一或不存在，贸然直接来个没意义，这是极其荒诞的，对科学是极其不负责任的、不严谨的，必须予以修正。