结合点云占比和平滑度的碗状碎块内表面识别算法
孙进 丁煜 王宁 习俊通 朱兴龙

摘 要:基于内表面特性的碗状碎块重组算法可有效避免由断裂曲面引起的過分割问题,但其难点在于内表面的准确提取,为此提出一种结合点云占比和平滑度的碗状碎块内表面识别算法。首先基于区域生长算法将碗状碎块的表面分割成断裂曲面、底面、原始表面、内表面和外表面;然后根据其点云占比的显著差异从中识别出内表面和外表面,最后利用平滑度提取内表面。实验结果表明该算法能实现碗状碎块内表面的准确提取,并且具有更快的运算速度。
关键词:点云占比;平滑度;碗状碎块;内表面;识别
DOI:10.15938/j.jhust.2020.03.024
中图分类号: TP301.6
文献标志码: A
文章编号: 1007-2683(2020)03-0157-06
Abstract:The bowl-shaped broken pieces reassembly algorithm based on the inner surface characteristics can effectively avoid the over segmentation problem caused by the fracture surface, while the difficulty lies in the accurate extraction of inner surface. Therefore, an identification algorithm for inner surface of bowl-shaped broken pieces based on point cloud proportion and smoothness is proposed. Firstly, the surface of bowl-shaped broken pieces is divided into fracture surface, bottom surface, original surface, inner surface and outer surface based on the region growing algorithm. And then, according to the significant difference of point cloud proportion, the inner surface and outer surface are identified from the segmented surface group. Finally, the inner surface is extracted by the smoothness value. The experimental results show that this algorithm can accurately extract the inner surface of bowl-shaped broken pieces and has a higher calculation speed than other algorithm.
Keywords:point cloud proportion; smoothness; bowl-shaped broken pieces; inner surface; identification
0 引 言
人类悠久的文明使得河流、湖泊、海洋下隐藏着众多的文化遗迹。以近期结束清理工作的“南海一号”为例,从这艘沉船打捞出的十四多万件文物中有九成以上是以碗状器型存在的瓷器[1]。这些水下文物在水底经过长时间的侵蚀和颠簸,大多数变得破碎残缺。由于破损文物数量众多,利用计算机辅助技术将其数字化后进行虚拟拼接,对水下文物的保护有着十分重要的意义。为便于文物数字化表征,基于厚度值大致将破损物体分为两类:厚度小于1mm的如纸币、油画[2]和地图[3]等,称为碎片;厚度大于1mm的如碗、壁画[4]和兵马俑[5]等,称为碎块。考虑到水下文物中大部分是以碗状器型存在的物件,故本文以碗状碎块为研究对象。
在三维碎块拼接领域,传统的碎块重组算法主要围绕断裂曲面的几何特征[6]展开,因此许多专家学者提出了关于断裂曲面的识别算法。如清华大学的Huang等[7]使用积分几何量勾勒出碎块各曲面的特征,并基于曲面局部弯曲能量进行断裂曲面的识别。在曲面局部弯曲能量的基础上,2017年,雅典经济与商业大学Papaioannou等[8]结合球体体积积分不变量来表征曲面特性,然后通过阈值来判别曲面是否是断裂曲面。2018年,西北大学的赵夫群[9]利用曲面的平均粗糙度数值来认定断裂曲面,但是上述算法过于依赖给定的阈值范围,其普适性需要实验验证。此外雅典国立科技大学的Papaodysseus等[10]通过提取壁画碎块上下平面之间最大连通子集片段来识别断裂曲面。2014年,岩手大学的Altantsetseg等[11]根据空间点的曲率检测得到曲面的脊点和谷点,然后通过基于距离的聚类算法累计脊点和谷点的数量从而识别出碎块的断裂曲面。2015年,路易斯安那州立大学的Zhang等[12]通过提取曲率值较高的点建立最小生成树,并将这些点连接成的曲线来代表断裂曲面的轮廓曲线,从而在碎块中识别出断裂曲面。2016年,西北大学的李群辉[13]根据高斯曲率和平均曲率判断曲面顶点的凹凸性,然后对凹凸点进行聚类实现断裂面的识别。2017年,首尔大学的Son等[14]利用法向量方差,二面角和成对距离描述断裂曲面的凸域和凹域,并定义曲面识别标志来提取断裂曲面。
上述断裂曲面的识别算法存在两个共性问题:一是对于几何信息不明显的断裂曲面来说,容易在匹配三维碎块的过程中产生拼接错误,从而导致拼接算法准确率的下降;二是对于几何信息丰富的断裂曲面来说,容易在曲面分割时产生过分割现象,从而在提取特征前需要合并过分割的断裂曲面,增加了拼接过程的时间。相较于断裂曲面可能存在的问题,内表面除了几何信息,还拥有比断裂曲面更丰富的颜色信息和纹理信息,可防止拼接过程中因使用单一特征所导致的拼接失误;同时内表面的识别算法不需要对断裂曲面分割后产生的众多曲面进行合并,仅需正确区分断裂曲面和内表面即可,可避开过分割带来的问题。因此本文提出一种结合点云占比和平滑度的碗状碎块内表面识别算法。
1 曲面分类的概述
在一般的碎块模型中,主要存在两种类型的曲面:断裂曲面和非断裂曲面,通常可以根据曲面的粗糙程度来识别断裂曲面。相比于非断裂曲面,断裂曲面上空间点的法向量变化程度更大,表面更凹凸不平。为描述曲面全局或局部空间的几何差异,引入弯曲能量[7]来表示其曲面粗糙度:
设置一个以p为球心,r为半径的包围球,则点p在邻域Br(p)内的局部弯曲能力定义为
其中:n为曲面S上的空间点个数。若平均粗糙度ρ(S)大于给定阈值ρ′,则曲面S可判定为断裂曲面。
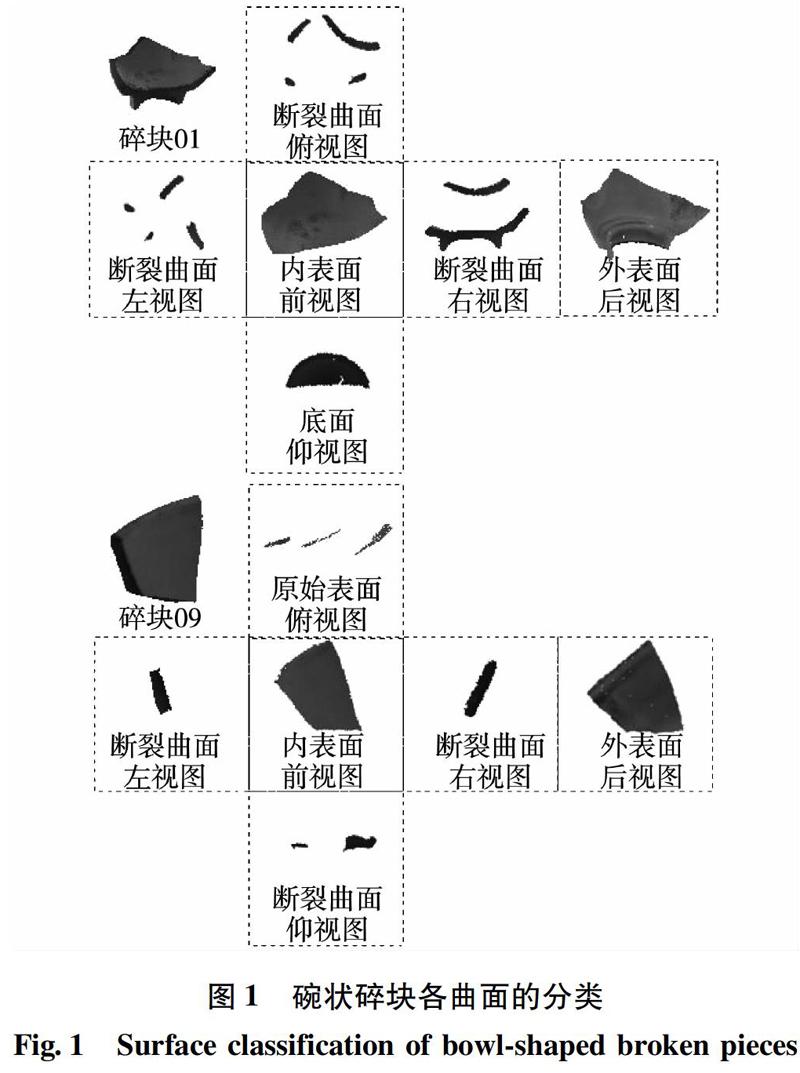
而对于碗状碎块的点云数据模型,采用区域生长算法[15]经过曲面分割后,可以将非断裂曲面细分为底面、原始表面、外表面和内表面4种类型。其中底面指的是碗状物体底部的曲面,外表面指的是碗状碎块外侧的曲面,内表面指的是碗状碎块内侧的曲面,原始表面指的是区域生长算法在外表面和内表面交界处过度分割的曲面,这部分曲面表面积较小,仅存在外表面和内表面相邻的部分碗状碎块中。曲面的分割结果如图1所示。
2 内表面的识别
2.1 点云占比
点云占比主要受两方面因素的影响:三维扫描仪的扫描原理和碎块自身的几何形态。与颜色特征和曲率等几何特征不同,受到测量过程中人为因素、环境因素或者测量方式的影响,点云占比通常无法精准反映碎块的表面特征。然而在使用相同的扫描方式和尽量避噪声点干扰的前提下,点云占比可以定性地反映碎块曲面的性质。
本文采用点云占比定性分析碗状碎块各分割曲面的性质。这主要是因为相比于其他类型的碎块,碗状碎块的厚度较薄,导致其外表面和内表面的表面积要大于其他曲面,也造成外表面和內表面的点云占比明显大于其他曲面。点云占比可以描述碎块中各分割曲面的大小,数值上等于曲面的空间点个数在碎块点云中所占的百分比。假设碗状碎块共有φ个分割曲面,且曲面Sφ(1≤φ≤φ)的空间点个数为Gφ,则曲面Sφ的点云占比可表示为
通常根据各个曲面的点云占比,可以从碗状碎块的众多分割曲面中识别出外表面和内表面。
2.2 平滑度
考虑到碗状物体在平时生活中的实际应用,外表面常用于抓取接触,内表面要便于清洗使用,而且一般情况下外表面还会设计一些凸出的纹饰特征,因此内表面一般比外表面更加光滑平整。数学表征为:相比于外表面,内表面上某一空间点的法向量与其周围点的法向量变化程度较小。为定量表征,本文引入平滑度的概念。
由于曲面上任意一点的法向量求取方法近似于计算曲面的一个相切面的法向量,因此曲面上任意一点的法向量计算可转化成一个最小二乘法的平面拟合估计问题。在三维空间坐标下,曲面Sφ可视作由l个点构成,即Sφ={p1,p2,…,pl},其中第 α个点pα(1≤α≤l)周围有m个邻域点pβ(1≤β≤m),那么这些点的质心pc可以表示为
利用最小二乘法拟合pα所在的局部曲面,通过求解局部曲面的法向量来表示pα的法向量,此时可以构建局部曲面的3×3协方差矩阵[16]:
矩阵M的3个特征值分别为a,b,c,其中a≤b≤c,最小特征值a所对应的特征向量即为pα的法向量,那么曲面Sφ的平滑度εφ可以表示为
其中φα,β为pα的法向量与其邻域点pβ的法向量的夹角。
εφ的大小可以定量地反映曲面Sφ的平滑度。曲面中相邻点之间的法向量变化愈小,则说明曲面的平滑度愈大。一般来说,碗状碎块的内表面平滑度数值要大于外表面。
2.3 内表面识别算法
结合碗状碎块的数据特点,本文依据点云占比和平滑度从碗状碎块的众多分割曲面中识别出内表面,识别算法如图2所示。具体步骤如下:
步骤1:新建集合Ω,放入碗状碎块的φ个分割曲面,即Ω={S1,S2,…,Sφ};
步骤2:计算Ω中每个曲面的点云占比PΩ,即PΩ={P1,P2,…,Pφ}。将点云占比的数值从大到小排列Psort={Pmax1,Pmax2,…,Pmaxφ},相对应的曲面为Ωsort={Smax1,Smax2,…,Smaxφ},则挑选出点云占比数值最大的两个曲面Smax1和Smax2放入新建集合Φ中,待进一步识别;
步骤3:分别计算集合Φ中Smax1和Smax2的平滑度数值εmax1和εmax2。如果εmax1>εmax2,则曲面 Smax1可判定为碗状碎块的内表面,曲面Smax2为碗状碎块的外表面;否则,曲面Smax2可判定为碗状碎块的内表面,曲面Smax1为碗状碎块的外表面。
3 实 验
3.1 实验结果
文中碗状碎块三维点云数据由Einscan-S三维激光扫描仪采集。软件架构为Visual Studio 2010,VTK 5.8.0(Visualization Toolkit,视觉化工具函式库)和PCL1.7.2(Point Cloud Library,点云库),在Intel Core i3-4160 CPU@3.60Hz处理器,4.0GB内存的PC上运行。实验选用12个不同的碗状碎块进行。
首先采用区域生长算法对碗状碎块进行曲面分割,图3为碗状碎块的分割结果。结合上文中的图1可以看出,碎块01的表面由断裂曲面、底面、内表面和外表面组成;碎块09的表面由断裂曲面、原始表面、內表面和外表面组成。同时统计分割后得到的曲面数量,结果如表1所示。
然后根据其点云占比的显著差异,从分割曲面组中识别内表面和外表面。图4为碗状碎块各分割曲面的点云占比分布图,从左至右依次是12个碎块中各分割曲面的点云占比计算结果。从实验结果可以看出,外表面和内表面的点云占比数值明显大于其他类型的曲面。基于点云占比的曲面识别方法优势在于算法简单,充分利用了碗状碎块的厚度特性,可以准确地从各分割曲面中识别出外表面和内表面。
最后利用平滑度提取内表面。图5为各碎块中内表面和外表面的平滑度计算结果,将曲面识别结果与曲面性质进行比对,12个碎块的内表面平滑度数值均大于外表面的平滑度数值,与2.2节中的理论判断一致,从而证明通过计算平滑度数值可以准确区分碗状碎块的内表面和外表面。
3.2 实验分析
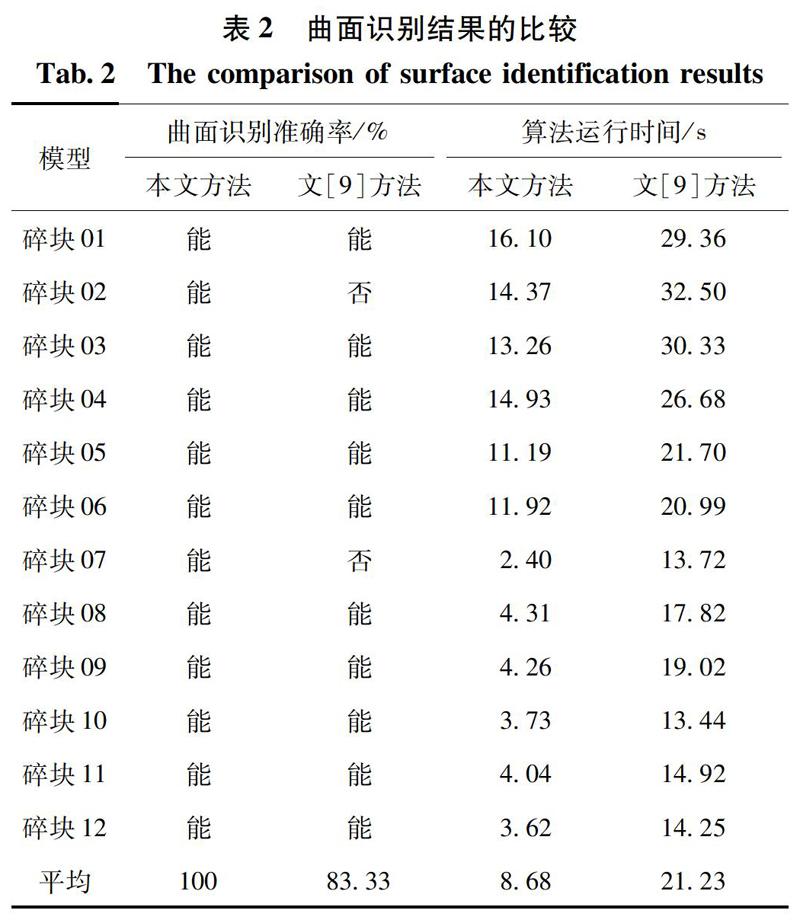
如表2所示,将本文所提出的结合点云占比和平滑度的算法用于识别碗状碎块的内表面,将文[9]所提出的曲面粗糙度法用于识别碗状碎块的断裂曲面,从而对12个碗状碎块的曲面识别结果进行进一步分析。在部分碗状碎块中,底面或原始表面的凹凸程度与断裂曲面的凹凸程度相近,同时固定阈值导致了曲面粗糙度法的错误识别,统计结果表明曲面粗糙度法的曲面识别准确率为83.33%。而采用点云占比可以正确区分内外表面和其他类型的曲面,同样平滑度帮助本文算法成功识别12个碗状碎块的内表面,因此本文算法比曲面粗糙度法的曲面识别准确率提高了20.00%。另外,对比文[9]的计算式(1)~(3)和本文算法的计算公式(7),结合点云占比和平滑度的计算方法更加简便,而且无需对过分割的断裂曲面进行合并,因此本文算法的平均运算速度比曲面粗糙度法的平均运算速度提高了144.63%。综上所述,采用点云占比和平滑度相结合的算法在识别碗状碎块的内面上更具备优越性,该算法拥有更高的曲面识别准确率和更快的运算速度。
4 结 论
传统的碎块重组算法在曲面分割过程中容易产生由断裂曲面引起的过分割问题,基于内表面特性的碗状碎块重组算法可以有效避免这一问题。为了能够准确提取内表面,本文提出一种结合点云占比和平滑度的碗状碎块内表面识别算法。该算法首先采用区域生长算法对碗状碎块进行曲面分割,然后通过计算各分割曲面的点云占比从众多曲面中识别出内表面和外表面,最后再利用平滑度区分出内表面。实验结果证明该算法可以成功识别所有碗状碎块的内表面,而且相比于用来识别断裂曲面的曲面粗糙度法,本文算法在曲面识别准确率上提高了20.00%,在平均运算速度上快了144.63%。另外,结合点云占比和平滑度的内表面识别算法不需要合并过分割的断裂曲面,可以从根本上提高碎块重组的效率,同时内表面还拥有比断裂曲面更丰富的颜色纹理信息,可防止碎块重组过程中因使用单一特征所导致的拼接失误。在今后的工作中应该继续研究不同类型碎块的内表面识别方法,为后续基于内表面特性的碎块重组与复原建立坚实的基础。
参 考 文 献:
[1] 黎继立, 何斌, 刘卫东, 等. 南海一号出水景德镇窑与龙泉窑青瓷特征的无损分析研究[J]. 光谱学与光谱分析, 2016, 36(5): 1500.
LI Jili, HE Bin, LIU Weidong, et al. Nondestructive Analysis of Jingdezhen and Longquan Celadon Wares Excavated from Nanhai No.1 Shipwreck[J]. Spectroscopy and Spectral Analysis, 2016, 36(5): 1500.
[2] EFTHYMIA T, IOANNIS P. Automatic Color Based Reassembly of Fragmented Images and Paintings[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2010, 19(3): 680.
[3] ZHANG M, CHEN S, SHU Z, et al. Fast Algorithm for 2D Fragment Assembly Based on Partial EMD[J]. The Visual Computer, 2017, 33(12): 1601.
[4] BROWN B, LAKEN L, DUTRE P, et al. Tools for Virtual Reassembly of Fresco Fragments[J]. International Journal of Heritage in the Digital Era, 2014, 1(2): 313.
[5] 高宏娟, 耿國华, 王飘. 基于关键点特征描述子的三维文物碎片重组[J]. 计算机辅助设计与图形学学报, 2019, 31(3): 393.
GAO Hongjuan, GENG Guohua, WANG Piao. 3D Archaeological Fragment Reassembly Based on Feature Descriptors of Key Points[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(3): 393.
[6] PAPAIOANNOU G, THEOHARIS T. Fast Fragment Assemblage Using Boundary Line and Surface Matching[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. Madison, Wisconsin, USA: IEEE Conference on Computer Vision and Pattern Recognition Workshop, 2003: 1.
[7] HUANG Q, SIMON F, GELFAND N, et al. Reassembling Fractured Objects by Geometric Matching[J]. ACM Transactions on Graphics, 2006, 25(3): 569.
[8] PAPAIOANNOU G, SCHRECK T, ANDREADIS A, et al. From Reassembly to Object Completion[J]. Journal on Computing and Cultural Heritage, 2017, 10(2): 1.
[9] ZHAO Fuqun, ZHOU Mingquan, GENG Guohua, et al. Rigid Blocks Matching Method Based on Contour Curves and Feature Regions[J]. IET Computer Vision, 2018, 12(1): 76.
[10]PAPAODYSSUS C, ARABADJIS D, EXARHOS M, et al. Efficient Solution to the 3D Problem of Automatic Wall Paintings Reassembly[J]. Computers & Mathematics with Applications, 2012, 64(8): 2712.
[11]ALTANTSETSEG E, MATSUYAMA K, KONNO K. Pairwise Matching of 3D Fragments Using Fast Fourier Transform[J]. The Visual Computer, 2014, 30(6/8): 929.
[12]ZHANG Kang, YU Wuyi, MANHEIN M, et al. 3D Fragment Reassembly Using Integrated Template Guidance and Fracture-region Matching[C]//2015 IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 2138.
[13]李群輝, 张俊祖, 耿国华, 等. 基于凹凸区域的断裂面匹配算法[J]. 计算机工程与应用, 2016, 52(13): 187.
LI Qunhui, ZHANG Junzu, GENG Guohua, et al. Fractured Surfaces Matching Based on Concave-convex Regions[J]. Computer Engineering and Applications, 2016, 52(13): 187.
[14]SON Taegeun, LEE Jusung, LIM Jeonghun, et al. Reassembly of Fractured Objects Using Surface Signature[J]. Visual Computer, 2017, 15(2): 1.
[15]李仁忠, 刘阳阳, 杨曼, 等. 基于改进的区域生长三维点云分割[J]. 激光与光电子学发展, 2018, 55(5): 325.
LI Renzhong, LIU Yangyang, YANG Man, et al. Three-Dimensional Point Cloud Segmentation Algorithm Based on Improved Region Growing[J]. Laser & Optoelectronics Progress. 2018, 55(5): 325.
[16]ZHANG Yuhe, GENG Guohua, WEI Xiaoran, et al. A Statistical Approach for Extraction of Feature Lines from Point Clouds[J]. Computers & Graphics, 2016, 56(S1): 31.
(编辑:温泽宇)

