大型电机定子铁心片间短路故障分析
孟大伟 王晓慧


摘 要:为了分析大型电机定子铁心片间短路故障,对故障模型的建立进行了研究。依据均质化理论,研究出铁心片间短路故障模型。建立了片间短路故障模型的等效电路,并给出了利用均质化求解的等效电导率表达式,对三维涡流场片间短路故障模型进行计算与分析,最后通过片间短路故障实验验证文中所提均质化建模方法的正确性与有效性。结果证明:故障处的电压要远大于非故障处;齿部故障区域的电压大于轭部故障区域的电压;故障片数越多,电压越大。实验结果与有限元分析结果相吻合,说明均质化建模法可以进行片间短路故障模型分析。
关键词:片间短路;均质化;等效电路;有限元
DOI:10.15938/j.jhust.2020.03.007
中图分类号: TM343.4
文献标志码: A
文章编号: 1007-2683(2020)03-0040-07
Abstract:In order to analyze the short circuit fault between the stator core pieces of large motors, the establishment of the fault model was studied. According to the homogenization theory, the short-circuit fault model between iron cores is studied. The equivalent circuit of the inter-chip short-circuit fault model is established, and the equivalent conductivity expression using homogenization is given. The three-dimensional eddy current inter-slice short-circuit fault model is calculated and analyzed. Finally, the inter-chip short-circuit fault test is passed. Verify the correctness and effectiveness of the homogenization modeling method proposed in the paper. The result proves that the voltage at the fault is much larger than the non-fault; the voltage in the fault area of the tooth is greater than the voltage in the fault area of the yoke; the more the number of faults, the larger the voltage. The experimental results are consistent with the results of finite element analysis, indicating that the homogenization modeling method can analyze the inter-chip short-circuit fault model.
Keywords:inter-chip short circuit; homogenization; equivalent circuit; finite element
0 引 言
定子鐵心片间短路故障产生的原因主要是铁心片间绝缘被破坏[1-2]。片间故障处的故障电流所产生额外的损耗和热量会破坏叠片间的绝缘,扩大故障的等级,甚至会引起叠片烧毁或融化[3]。因此需要对定子铁心片间短路故障进行研究,以保障电机安全稳定运行。
进行片间短路故障分析,建立准确的铁心片间短路模型尤为重要。铁心损伤电磁感应检测法[4]可以直接分析片间短路故障,但铁心片间短路故障的试验操作难度较高,且对电机的破坏性较大。目前,铁心建模的方法主要是有限元法、解析法和等效电路法。文[5]采用解析法建立硅钢片铁心模型,利用麦克斯韦方程推导铁心阻抗表达式,同时考虑铁心等效磁导率的频变特性,但由于计算过程比较复杂,仅仅进行理论分析。文[6-7]的有限元分析方法不仅可以计算出在铁心故障时产生的涡流及涡流损耗,也可以为了满足设计的需要而调整参数,但要求对每片硅钢片都进行非常细致的剖分,这会导致巨大的计算代价,出现仿真时间过长的问题。文[8]为了避免这个问题的出现,提出铁心均匀化建模方法,即用一种均质化媒质代替叠片铁心,并进行有限元的仿真分析。文[9]对铁心及叠片间的绝缘系统进行分析,根据等效前后的硅钢片中的经典涡流损耗相等,采用等效电路法将一片硅钢片等效成一个电势和两个电阻,进而推导出n片硅钢片叠成铁心后的等效电路。
为研究均质化方法在模拟铁心片间短路故障的有效性,本文根据均质化方法的基本原理,利用等效电路法求解出故障区域的等效电导率[8];同时运用有限元软件,建立了三维涡流场铁心片间短路故障模型;最后,通过片间短路故障实验验证文中所提均质化建模方法的正确性与有效性。
1 等效电导率和磁导率
1.1 非故障情况下的铁心等效电导率和磁导率
当采用实际叠片模型进行有限元仿真时,需要对每片硅钢片都进行非常细致的剖分,工作量巨大;且各向同性电导率不能有效地分析垂直于叠片方向的涡流。因此,可以采用均质化理论将实际叠片等效成连续体模型,求出铁心的等效电导率和等效磁导率。根据文[10],垂直于叠片方向的等效电导率可以通过下面的式子获得:
由于铁心绝缘层的电阻远远大于硅钢片电阻,可以近似看成涡流仅仅存在于硅钢片内部,因此对于垂直叠片平面方向的电导率可以近似设置为0。因此,在确保相对精度的基础上,传统均质化方法[11]可以进一步化简式(1)的各向异性电导率模型,等效电导率表示为:
1.2 故障情况下的铁心等效电导率和磁导率
文[12]中,故障区域等效电导率表示成:
对于故障区域,由于故障程度的不同,垂直于叠片方向的等效电导率会有不同的改变,但以往文献中并没有细致的分析铁心叠装方向的电导率,仅仅给了一个粗略的计算,这就导致之后的有限元仿真分析会存在误差,因此需要重新建立求解故障区域的铁心等效电导率。
对于处于时变磁场中的铁心硅钢片,其内部将感应涡流,涡流的抗磁性将使硅钢片中磁通的分布不均匀产生集肤现象,磁场只穿透一定的深度,这种效应被称为集肤效应。
图1为处于交变磁场激励下的一块硅钢片,厚度为d,长度为L,宽度为W,电导率为σ,磁导率为μ,磁场频率为f。
由图1所示,根据硅钢片中电流的流通路径可以把单片硅钢片的等效电阻分为x轴和y轴两个方向,分别记为R1、R2。R1和R2可分别由如下公式计算:
其中:δ为集肤深度,可由以下公式得到:
实际电机定子铁心由多层硅钢片叠成,由于每片硅钢片中磁场的分布规律近似相同,若發生n(n>1)片硅钢片的局部片间短路故障,假设这个局部故障区域的绝缘层完全破损,则可建立n片硅钢片故障区域与单片硅钢片之间的联系,如图2所示。
根据图2所示的n片硅钢片片间短路故障时故障电流的流通路径,可以得出图3所示的等效电路图,图3可以近似看为故障区域的等效电路,从而可以求出故障区域的等效电阻为:
由图2所示,根据实际的片间绝缘故障,故障区域的硅钢片可看作块状导体模型,故障电流同样会由于集肤效应导致其故障电流主要集中于故障区域表面,也可以将故障区域的等效电阻表示为:
式中,δy为故障区域中故障电流在y方向(平行于叠片方向)上的集肤深度,δx为故障区域中故障电流在x方向(垂直于叠片方向)上的集肤深度,可表示为:
由此可以推出故障区域垂直于叠片平面方向的电导率:
因此,片间短路故障时叠片铁心的各向异性等效电导率可以表示成:
2 有限元建模分析
2.1 数学模型的建立
铁心发生片间短路时会形成故障区和非故障区两部分。本文使用的T-ψ方法[14-16]不仅通过减小未知数的总数缩小了计算规模,而且保证了相对精度。
1)故障区域
电流密度J和磁场强度H可通过矢量电位T和标量磁位ψ进行求解:
2)非故障区域
磁场强度H的求解可以通过标量磁位ψ
T和ψ的典型边界条件为T的切向分量和J的垂直分量。
由于故障区域和非故障区域之间存在接触面问题,所以将故障区域的T-ψ方程、与非故障区域的ψ联立成T,ψ-ψ方程[17-18],通过设置T×n为零即可满足T,ψ-ψ方程边界条件J·n=0[19]。
2.2 三维涡流场模型的建立
根据均质化方法提出的等效电导率和等效磁导率来建立有限元模型。本文选用YR630-12/1430绕线型异步电动机定子铁心为样机模型,具体参数如表1所示。
本文所采用的定子铁心材料为DR530-50,具体的材料参数如表2所示。
首先将电机定子冲片划分成Q1(定子槽数)个小单元组成,由于对称关系,只分析其中一个单元(如图4所示)即可。每个单元又分为齿部和轭部区域,在每个单元的齿部区域或轭部区域发生故障的情况下,假设各个区域的硅钢片近似认为完全故障。
本文分为两种情况,每一种情况取一个小单元为故障分析对象:
1)在定子铁心齿部和轭部分别设置深度为1mm(2片故障)的故障区域;
2)在定子铁心齿部和轭部分别设置深度为2mm(4片故障)的故障区域。
有限元方法使用T,ψ-ψ方程对三维涡流场进行分析,采用自适应网格剖分方法可以有效地完成铁心区域的剖分,得到网格剖分如图5所示。
仿真计算得到的铁心涡流密度分布云图如6、7所示。
可以观察到涡流主要集中在定子故障区域,定子铁心不同故障处的涡流密度也有较为明显的差异。定子铁心在两种情况下各个故障部位的涡流密度分布云图如图8、图9所示。
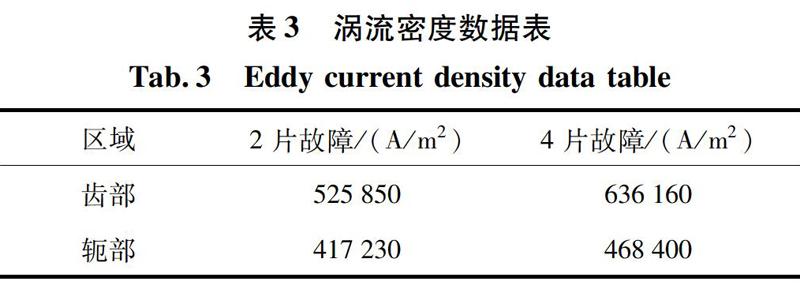
为形象地说明不同故障程度、不同故障部位的涡流情况,由图8、图9提取出的涡流密度最大值引入表3。
数据对比分析可得以下结论。
1)非故障区域,硅钢片片间形成的涡流极小,可忽略不计;故障区域具有非常明显的涡流效应,涡流密度幅值远大于非故障区域的值。
2)当故障片数相同时,齿部故障区域的涡流密度大于轭部故障区域的涡流密度。
3)同一故障区域,故障片数越多,涡流密度越大。由此可见,随着片间短路故障程度的加剧,电流密度呈上升趋势。
3 铁心片间短路故障实验
為了验证研究方法的合理性及仿真结果的准确性,选用YR630-12/1430绕线型异步电动机定子铁心为样机模型,实验装置见图10。进行故障检测实验的准备工作:
1)实验采用低励磁法[20],励磁电压为1.4V;
2)图10中励磁绕组位于定子腔内的轴线处,为了避免对铁心中的磁场产生干扰,铁心端部与励磁绕组的距离应不小于1m;
3)区域的模拟:使用电钻头分别在定子齿部和轭部区域各钻深度为1mm和深度为2mm的故障区域,并将该洞焊接上确保故障电流回路的形成。
手持装有传感器探头的小车,并以一定的速度沿槽的方向移动小车,传感器探头实时采集定子铁心磁场的信息,经过处理后,通过以太网上传至上位机,进行电压波形显示,分别将不同故障情况下的电压数据提取出来,再利用前面的电路与磁场模型,建立新的约束条件重新求解,得出非故障区域和故障区域的感应电压数值。将仿真结果与实验结果进行对比,如表4所示。
由表4数据可知:故障处的电压要远大于非故障处;齿部故障区域的电压大于轭部故障区域的电压;故障片数越多,电压越大。有限元仿真的感应电压变化趋势与实验检测电压的变化趋势有较好的一致性,验证了有限元分析所得到结论的正确性,说明利用均质化方法建立的仿真模型具有准确性,可以用来模拟定子铁心的片间短路故障。
4 结 论
对基于均质化理论推导出故障区域等效电导率,较准确地分析计算了片间短路故障时铁心的相关参数,定量分析了不同情况对铁心故障参数的影响,给出了故障部位、故障片数不同时铁心参数的变化规律,并用实验加以验证。结果表明:仿真结果与实验检测结果相吻合,验证了本文研究方法以及分析结果的正确性;故障区域的涡流密度及检测电压远远大于非故障区域;齿部故障处涡流密度及检测电压要比轭部故障处略大;故障处的涡流密度及检测电压随着故障片数的增多而加大。
参 考 文 献:
[1] ASHERAF E, FATIH A. Evaluation of Loss Generated by Edge Burrs in Electrical Steels[J].IEEE Transactions on Magnetics, 2016, 52(5): 1404.
[2] SANG Bin Lee, GERALD, KLIMAN B, et al. An Advancedtechnique for Detecting Inter-laminar Stator Core Faultsin Large Electric Machines[J].IEEE Transactions on Industry Applications, 2005, 41(5): 1185.
[3] 姜茜. 汽轮发电机定子铁心故障[J].东方电机, 2011 (5):72.
JIANG Qian. Fault of Stator Core of Turbo-generator [J] .Dongfang Electric, 2011 (5): 72.
[4] 贾志东, 白雨, 张征平, 等. 用于发电机定子铁芯的铁芯损伤电磁感应检测法检测原理析[J].高电压技术, 2015, 41(1):123.
JIA Zhidong, BAI Yu, ZHANG Zhengping, et al. Analysis on the Detection Principle of Electromagnetic Induction Detection Method for Iron Core Damage of Generator Stator Core [J] .High Voltage Technology, 2015, 41 (1): 123.
[5] 王增超. 10kV電力变压器非线性宽频建模方法研究[D].北京:华北电力大学, 2015.
[6] 李静. 有限元方法在电磁场分析中的应用[D].重庆: 重庆师范大学, 2011.
[7] 刘国强. Ansoft工程电磁场有限元分析[M].北京:电子工业出版社, 2005.
[8] 周立军, 刘桓成, 高仕斌, 等. 考虑多点接地故障的变压器铁心均匀化建模方法[J].中国电机工程学报, 38(12):3709.
ZHOU Lijun, LIU Huancheng, GAO Shibin, et al. Modeling Method of Transformer Core Uniformity Considering Multi-point Ground Fault [J] .Transactions of China Electrical Engineering, 38(12):3709.
[9] 李文平. 大型变压器铁心片间绝缘的分析[J].变压器, 1993(11):17.
LI Wenping. Analysis of Insulation Between Core Pieces of Large Transformer [J] .Transformer, 1993(11):17.
[10]WANG Jian, LIN Heyun, HUANG Yunkai, et al. A New Formulation of Anisotropic Equivalent Conductivity in Laminations[J].IEEE Transactions on Magnetics, 2011, 47(5): 1378.
[11]王坚. 永磁涡流传动技术基础理论研究[D].南京:东南大学, 2014.
[12]孟大伟, 肖利军, 孟庆伟. 考虑定子铁心片间短路时的涡流及涡流损耗的有限元分析[J].电工技术学报, 2014, 29(7):19.
MENG Dawei, XIAO Lijun, MENG Qingwei. Finite Element Analysis of Eddy Current and Eddy Current Loss Considering Short Circuit Between Stator Core Pieces [J] .Transactions of China Electrotechnical Society, 2014, 29 (7): 19.
[13]孟大伟, 肖利军, 徐永明, 等.多频情况下存在绝缘故障的叠片铁心的涡流及涡流损耗的分析[J].电工技术学报, 2015, 30(6): 92.
MENG Dawei, XIAO Lijun, XU Yongming, et al. Analysis of Eddy Current and Eddy Current Loss of Laminated Cores with Insulation Faults at Multi-Frequency [J] .Transactions of China Electrotechnical Society, 2015, 30 (6): 92.
[14]REN Z. Formulation for Eddy-current Problems in Multiply Connected Regions[J].IEEE Trans Magn, 2002, 38(2): 557.
[15]BIR O, PREIS K, TIAR I. Voltage-Driven Coils in Finite-Element Formulations Using a Current Vector and a Magnetic Scalar Potential[J].IEEE Trans Magn, 2004, 40(2): 1286.
[16]谢德馨. 三维涡流场的有限元分析[M].北京: 机械工业出版社, 2008.
[17]ALBERTZ D, HENNEBERGER G. Calculation of 3D EddyCurrent Fields Using both Electric and Magnetic Vector Potential in Conducting Regions[J]. IEEE Trans Magn, 1998, 34(5): 2644.
[18]SILVA V C. A 3D Finite-element Computation of Eddy Currents and Losses in the Stator End Laminations of Large Synchronous Machines[J].IEEE Trans Magn,1996, 32(3): 1569.
[19]BERMU' DEZ A, GMEZ D, SALGADO P. Eddy Current in Laminated Cores and the Computation of An Equivalent Conductivity[J].IEEE Tran Magn, 2008, 44(12): 4730.
[20]林海鵬. 大型发电机定子铁心片间短路检测系统设计[D].哈尔滨:哈尔滨理工大学, 2013.
(编辑:温泽宇)

