氢气泵自适应无迹卡尔曼滤波无传感器控制
Sheianov Aleksandr 康尔良


摘 要:提出了一種氢气泵用PMSM转子位置新型非线性估算方法。卡尔曼滤波常用于在非线性系统,在计算量相同的情况下,无迹卡尔曼滤波器(UKF)较扩展卡尔曼滤波器(EKF)的计算结果更为准确,因为应用较多。在燃料电池系统中,氢气泵用PMSM的负载常发生持续变化或突变;由于UKF采用固定过程噪声协方差(Q矩阵),无法响应负载变换造成的过程噪声变化,传统卡尔曼滤波器的性能可能下降。提出了一种自适应UKF方法,通过计算UKF的自适应增益,以补偿实际残差协方差与滤波器导出值之间的不匹配,从而在负载变换的情况下,保证了转子位置估算的精度。最后,搭建氢气泵用PMSM控制系统,并进行了自适应UKF转子位置估算。实验结果验证了该算法的可行性和有效性。
关键词:无传感器控制;自适应卡尔曼滤波;氢气泵
DOI:10.15938/j.jhust.2020.03.005
中图分类号: TM351
文献标志码: A
文章编号: 1007-2683(2020)03-0025-08
Abstract:This paper demonstrates a special and new type of non-linear observer for a permanent magnet synchronous motor used in hydrogen pump applications. For nonlinear systems, the unscented Kalman filter (UKF) is a very popular approach for the controller design. Some researches have shown that the UKF is usually more accurate than the extended Kalman filter (EKF) whereas the computation burden is the same in both cases. However, the performance of traditional Kalman filter may degrade when process noise and load are constantly changing or a sudden disturbance occurs due to the fixed process noise covariance (Q matrix) in the filter, which is the case in fuel cell systems where a hydrogen pump is used. An adaptive gain is calculated to compensate for the mismatch between the actual residual covariance and the deduced value from the filter, ensuring that the sequence of residual is uncorrelated. Also, the derivation of the proposed adaptive UKF is explained in details. Finally, experimental tests under sensorless position control for hydrogen pump are carried out with the proposed method, in which the feasibility and effectiveness of the algorithm is shown.
Keywords:sensorless control; adaptive unscented kalman filter; hydrogen pump
0 INTRODUCTION
Recently, sensorless permanent-magnet synchronous motor (PMSM) drive systems have gained much interest from industries as well as researchers because of the elimination of fragile and noisy rotor position sensors [1-3], [19-21]. In these drive systems, the speed and rotor position play a key role in the good performance of a closed-loop system, but these values cannot be directly estimated. Therefore, to obtain these values and then feed them into a controller and reference frame transformations, position estimator in the feed-back path is used. Usually the inputs to the estimator are the measured voltages and currents, and the outputs are the estimated speed and rotor position.
In the present, there are a number of types of observers in Kalmans family. A Kalman filter originally is a linear observer, also known as a linear quadratic estimator (LQE). The filter is named after Rudolf E. Kálmán, the developer of this theory. Kalman filter is widely used in applications such as guidance, navigation, and control of vehicles, particularly aircraft and spacecraft, because it gives the best performance among all of the linear estimators and observers. Also, for non-linear problems, the Kalman filters family provide a number of different approaches [4]. The most popular and most studied until now is the extended Kalman filter, which is used to compute the predicted state from the previous estimate first and then in the same manner, the output function h computes the predicted measurement from the forecasted state. However, in this type of filters f and h cannot be applied to the covariance directly. Therefore, a matrix of partial derivatives (the Jacobian) is calculated at each time step [5]. Although the extended Kalman filter (EKF) is relatively simple to apply for the motor control application, it has a number of major drawbacks:
1)relatively complex derivation of the Jacobian matrices in the linearization process.
2)it has only first-order accuracy, because higher-order terms are neglected.
3)Filter instability because of linearization.
Therefore,to help eliminate this problem and therefore make non-linear Kalman filters family be more accurate and superior to other non-linear algorithms, Julier and Uhlmann[6-7]proposed a new approach to improve the performance of non-linear Kalman filters. Instead of linearizing non-linear system at each time step(sovling Jacobian matrices) the UKF uses a minimal set of sample points, which are fed to the nonlinear-state equations to obtain the mean and covariance of a non-linear system in the prediction step and then use them to correct the predicted estimates according to the new measurements. The UKF has been proven to be more accurate than EKF with similar computation burden. It also has been successfully implemented in a few practical applications[7-8]such as: navigation, radar tracking, signal processing, neural networks, and robotics. The first implementation of the UKF in motor control was reported by Akin[9]. Tze-Fun Chan, Pieter Borsje and Weimin Wang [10], reported the application of the UKF for sensorless vector control of PMSM in d-q reference frame, whereas A.Titaouine, D. Taibi [11], realized this algorithm together with non-linear control of inverter [16], also Cheol Moon, Kee Hyun Nam [12], reported the results of the implementation of the UKF in alpha-beta reference frame. However, UKF still suffers some drawbacks from traditional Kalman filter. For the state estimation of a hydrogen pump, the pm motor may work in a various load conditions. Thus, a mismatch between the real process noise characteristic and the one in the filter usually occurs and the performance of the filter deteriorates. Besides, UKF might react slowly in cases when sudden disturbances occur in the system. Therefore, the adaptive UKF[13-15]is needed to overcome the drawbacks listed above. Xia, Rao et al. developed an adaptive fading Kalman filter (AFKF) for linear systems, which ensured the Kalman gain was optimal by making the auto-covariance of residual equal zero[17,22].
In this paper, an adaptive UKF is designed by adjusting the process noise covariance matrix Qk at each sample with an adaptive gain. The gain is calculated based on the optimal feature in [17] and real-time estimated k inspired by [18]. The proposed method is tested on the hydrogen pumps permanent magnet motor. Experimental results show that the proposed algorithm has a good performance in sensorless control and hydrogen pumps state estimation.
1 MODEL OF PMSM
The Kalman filter requires a mathematical model of the system in order to estimate the states of the system. Formulation of the mathematical model of a controlled system is an important task during the design stage of the estimator. The correct model can simplify the solution of the estimation problem as well as simplify the computational cost of the whole algorithm.
To avoid convergence problems at startup and to simplify the motor equations, the d-q reference frame is chosen for evaluation of the Kalman filters [2]. The motor nonlinear state equations can be expressed:
The UKF consists of four state variables: stationary reference frame currents, estimated speed and estimated angle. Since the mechanical variables have a tendency to change rapidly and are very hard to measure correctly, the state variables consists of only electrical variables. The state variable vector is then x=[id iq ωe θe]T. By taking the partial derivatives by x we can write the system state matrices (3) and (4):
2 UNSCENTED KALMAN FILTER
For sensorless control of PMSM using UKF, the motor nonlinear state equations (1) and (2) should be expressed in the discretized form (5)~(6):
The state model represented by (5) and (6) also includes the statistical description for the inaccuracies, where wk~N(0,Qk) and vk~N(0,Rk) are, respectively, the zero-mean Gaussian process noise and measurement noise vectors with covariance matrices Qk and Rk.
2.1 Unscented Transformation (UT)
Unscented Transformation (UT) is designed on the fact that it is easier to approximate a probability distribution than to approximate a nonlinear function(later is the principle the EKF is based on). But the most important is that the approximations are accurate up to the third order in case of Gaussian inputs. For non-Gaussian inputs, approximations are accurate to at least a second order. Therefore, the UKF is expected to give better performance and accuracy than the EKF which has only first-order accuracy.
Unscented Kalman filters, as in a classical form of the linear Kalman filter is based on two cycles which include prediction and correction. However, in the case of the UKF a set of sample points around the last state is taken and propagated through a nonlinear function (the PMSM model or PMSM nonlinear state transition and measurement functions). With these results a mean and covariance can be approximated using weighted sample mean and covariance of the transformed sample points. These weighted sample points are generated as follows. Consider the state variable x with dimension L having mean and covariance Px. We now choose a set of 2L+1 weighted samples χi (sigma points) deterministically so that they completely represent the true mean and covariance of state x. Following is how sigma points and weights determined:
where =α2(L+κ)-L indicates a scaling parameter. The superscripts m,c, express the weighted point for mean and covariance calculation. The value α determines the spread of the sigma points around x and usually it equals 10-4<α≤1. The constant κ is an another scaling parameter which is usually set to (3-L), and β is a prior knowledge of the distribution of x (for Gaussian distribution β=2 is optimal).
3)Each point is propagated through the nonlinear state transition and measurement functions to yield a set of transformed sigma points.
4)The mean and covariance of y are approximated by the weighted average mean and covariance.
2.2 UKF Algorithm
The UKF is a straightforward application of the UT to the recursiveKalman filter equations. Fig.1 shows the flowchart of the proposed algorithm, which involves the following steps:
In this paper, the author designs an adaptive UKF (AUKF)for state estimation of permanent magnet synchronous motor. In the application of a hydrogen pump system, load conditions varies according to the demand of the fuel cell system. Thus the characteristic of process noise is hard to predict before the implementation. Its possible for standard UKF that the estimator would have an unsatisfactory performance due to the model error or the difference between the real noise characteristic and the one used in the filter. Moreover, standard UKF filter may respond slowly if the disturbance occurs and measurements have a sudden change. The solution to the problems above is to adjust process noise covariance adaptively. In this paper, equation (17) is modified as:
where η(k) is a positive gain, and Qa.k is the adjusted process noise covarianve in discrete-time domain. The advantage of using Qa.k instead of original noise covariance matrix Qk is that the characteristic of each noise signal can be estimated adaptively.
The adaptive gain η(k) is derived first. In [17] Xia et al. proposed an adaptive fading linear Kalman filter which guaranteed that the sequence of residuals was uncorrelated by the following equation:
where Hk is the output matrix, and C0,k is the covariance of the residual. This idea is extended in the UKF adaptive scheme in this paper. Define the residual:
If weknow Qa,k, then adaptive gain can be computed. In the following, an estimation algorithm for process noise covariance matrix is designed. In [18], process noice covariance matrix is estimated on-line by:
whereФ is Jacobian matrix and Δxj is the difference between a posterior and a priori estimated state:
Using (32) in UKF scheme and use another fading factor ρ2 instead of the average operation in (32) to overweight the recent values, the real-time k is:
However, (34) may yield a k which is not positive-definite. To cope with this issue, some constraints must be introduced. When the sample time is small, the estimated c can be obtained if B′wBw is non-singular:
Since a relatively large process noise covariance matrix is needed to overcome the model error and sudden disturbances, very small diagonal elements in k is not suitable, which means that minimum values constraints must be set. Besides, the maximum values also need to be constrained because (34) is only an estimation. It is not realistic if the estimated covariance is very large. As a result, the constraints for the diagonal terms in estimated covariance matrix c are as follows:
where ξ is a large positive tuning parameter, d is the number of disturbances in (5) and C(i,i) is the ith diagonal element of c. Normalize the constrained c so that:
If we define this adjusted matrixas ′c, then the process noise covariance matrix Qa,k in (30) can be calculated as:
Substitute (38) into (31), the gain η(k) can be obtained. Since large process noise covariance can contribute to a quick response which is one of the main requirements in hydrogen pump application, therefore η(k) is set to be larger than 1,
Thediagram of the proposed sensorless control system is presented in Fig.2.
3 EXPERIMENTAL RESULTS
Experiments were carried out to confirm the effectiveness of the proposed design. The experimental setup shown in Fig. 3 consists of an IPMSM (1.5 kW) coupled with a hydrogen pump. The parameters of the motor are given below:
Rs=0.22Ω:stator resistance (phase to phase);
Lq=0.00217H:motor q-axis inductance;
Ld=0.00107H:motor d-axis inductance;
J=0.0001605N·m/rad/s:moment of inertia;
p=8:number of the poles;
nN=5000r/min:rated speed;
ψf=0.2614Wb:flux of the permanent magnet;
Vdc=300V:rated voltage.
The carrier frequency of the inverter is 10kHz, and Bw is an identity matrix. Tuning parameter κ,α and β in are 0, 0.01 and 2 respectively. Fading factor ρ1 in (32) and ρ2 in (34) are 0.4.
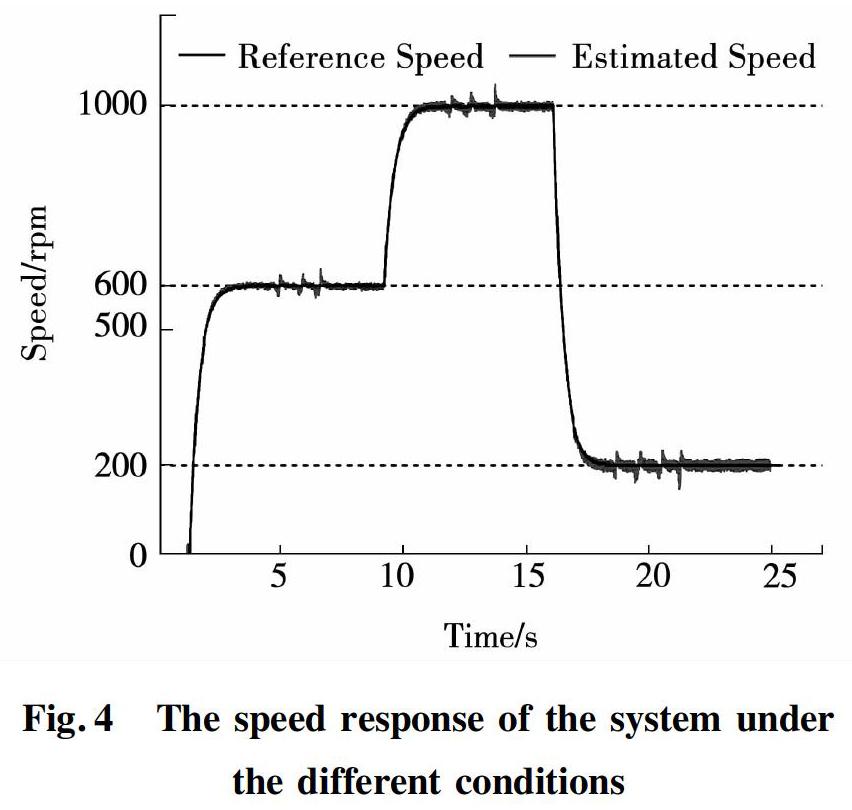
The tests were carried out under the condition of a half of the rated torque. During the steady-state operation of the motor some random disturbances were introduced to the system which emulated the real working conditions of hydrogen pump in a real fuel cell system. Fig 4. illustrates the speed sensorless control response under the reference speed ωref=600r/min, ωref=1000r/min and the changes of the load demand. It can be noticed that the system is completely robust against these changes as well as disturbances occured during the steady state operation, also the transient time is very short, which confirms the effectiveness of the proposed scheme.
Fig.5 shows the real and estimated rotor position. Themaximum value of the rotor position estimation error is 0.02 which is equivalent to 7°in the whole operation range. The phase current of the proposed method under a half of the rated torque and ωref=1000r/min are shown in Fig 6.
The only drawback of the proposed method is that it cant be implemented on a fixed-point processor, because it doesnt guarantee the convergence of the state covariance matrix. But it can be readily realized on a floating point processor with frequency more than 70MHz which has enough capability to calculate the whole sensorless control algorithm during one interrupt and the problem with convergence will not occur.
4 CONCLUSION
In this paper, the sensorless control of permanent magnet motor drive system using an adaptive Unscented Kalman filter (UKF) has been studied to improve the state estimation accuracy, robustness of the system and the overall performance of the motor drive system. The process noise covariance matrix is first estimated and restricted to maintain its positive definitiveness, and then an adaptive gain is introduced to ensure the sequence of output residuals is uncorrelated. Notice that the algorithm requires that the measurement model is linear. For the nonlinear case, the Jacobian matrix of measurement model can be used. Experimental test results validate that the proposed filter has the best performance compared with EKF, and standard UKF with the presence of disturbances, load changes and process uncertainty mismatch for sensorless control algorithm of permanent magnet motor used in hydrogen pump.
REFERENCES:
[1] YOU C J, LI J, HUANG X Y, et al. A Full-speed Sensorless Control Algorithm for Interior Permanent Magnet Synchronous Motor Using Sliding-mode Observer and hf Signal Injection[C]// Vehicle Power and Propulsion Conference (VPPC). Belfort, France: IEEE, 2017:1.
[2] YANG S C, HSU Y L, CHEN G R. Design Issues for Permanent Magnet Machine Sensorless Drive Combining Saliency-based and Back-emf-based Control in the Entire Speed Range[C]// International Conference on Industrial Technology (ICIT). Taipei, Taiwan: IEEE, 2016:1270.
[3] YANG P, XIAO X, ZHANG M, et al. High-precision Rotor Position Estimation for High-speed SPMSM Drive Based on State Observer and Harmonic Elimination[C]// The 2018 International Power Electronics Conference, Nigata, Japan, 2018:1966.
[4] SIMON D. Optimal State Estimation[M]. New Jersey: John Wiley & Sons, 2006.
[5] DHAOUADI R, MOHAN N, NORUM L. Design and Implementation of an Extended Kalman Filter for the State Estimation of a Permanent Magnet Synchronous Motor [J]. IEEE Transactions on Power Electronics, 1991, 6(3): 491.
[6] JULIER S J, UHLMANN J K. A New Extension of the Kalman Filter to Nonlinear Systems[C]// Signal Processing, Sensor Fusion, and Target Recognition VI. Orlando, FL, United States: AeroSense, 1997:182.
[7] MERWE R, WAN E A. Efficient Derivative-free Kalman Filters for Online Learning [C]// Proceeding of European Symposium on Artificial Neural Networks (ESANN), 2001:205.
[8] STENGER B, MENDONA P R S, CIPOLLA R. Model-based Hand Tracking Using an Unscented Kalman Filter[C]// Proceedings of the British Machine Conference, University of Manchester: BMVA Press, 2001:63.
[9] AKIN B, ORGUNER U, ERSAK A. State Estimation of Induction Motor Using Unscented Kalman Filter[C]// Proceedings of 2003 IEEE Conference on Control Applications, Istanbul, Turkey, IEEE, 2003:915.
[10]BORSJE P, CHAN T F, WONG Y K, et al. A Comparative Study of Kalman Filtering for Sensorless Control of a Permanent-magnet Synchronous Motor Drive[C]// International Conference on Electric Machines and Drives. San Antonio, TX, USA, IEEE, 2005:815.
[11]TAIBI D, BENNIS O, BENCHABANE F, et al. Adaptive Nonlinear Control Combined with Unscented Kalman Filter for Permanent Magnet Synchronous Motor Fed by AC/DC/AC Converter[C]// International Aegean Conference on Electrical Machines and Power Electronics and Electromotion, Istanbul, Turkey, IEEE, 2011:26.
[12]MOON C, NAM K. H, JUNG M. K, et al. Sensorless Speed Control of Permanent Magnet Synchronous Motor Using Unscented Kalman Filter[C]// SICE Annual Conference, Akita, Japan, IEEE, 2012:2018.
[13]QUANG N. K, TUNG D. D, HA Q. P. FPGA-based Sensorless PMSM Speed Sontrol Using Adaptive Extended Kalman Filter[C] // IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, IEEE, 2015:1650.
[14]LIU Z T, WANG Y Y, DU J N, et al. RBF Network-aided Adaptive Unscented Kalman Filter for Lithium-ion Battery SOC Estimation in Electric Vehicles[C] // IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, IEEE, 2012:1673.
[15]GAO B B, GAO S S, GAO L, et al. An Adaptive UKF for Nonlinear State Estimation Via Maximum Likelihood Principle[C]// 6th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, IEEE, 2016: 117.
[16]DARBA A, SALAHSHOOR K. EKF and UKF-based Estimation of a Sensorless Axial Flux pm Machine under an Internal-model Control Scheme Using a Svpwm Inverter[C] // Proceedings of the 29th Chinese Control Conference, Beijing, China, IEEE, 2010:5676.
[17]XIA Q, RAO M, YING Y, et al. Adaptive Fading Kalman Filter with an Application[J]. Automatica, 1994, 30(8):1333.
[18]MOHAMED A, SCHWARZ K. Adaptive Kalman Filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73( 4): 193.
[19]TIAN L, ZHAO J, SUN J. Sensorless Control of Interior Permanent Magnet Synchronous Motor in Low-Speed Region Using Novel Adaptive Filter [J]. Energies, 2016, 9(12):1084.
[20]AWAN H. A. A., TUOVINEN T, SAARAKKALA S. E, et al. Discrete-Time Observer Design for Sensorless Synchronous Motor Drives [J]. IEEE Trans. Ind. Appl., 2016, 52(5):3968.
[21]JUNG T U, JANG J H, PARK C S. A Back-EMF Estimation Error Compensation Method for Accurate Rotor Position Estimation of Surface Mounted Permanent Magnet Synchronous Motors [J]. Energies, 2017, 10(8):1160.
[22]CHUBICH V, CHERNIKOVA O. Adaptive Fading Kalman Filter with Applications in Identification Discrete System[C]// 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, IEEE, 2016:385.
(編辑:温泽宇)

