双弱面层状岩体本构模型及其工程应用

姚锡伟，周 辀，陶盛宇

(1.内江职业技术学院，四川 内江 641000；2.成都理工大学 环境与土木工程学院，四川 成都 610059； 3.地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

0 引言

在工程建设中,层状岩体是经常遇到的岩体之一，其物理、力学性质受到内部节理面、层理面等软弱结构面控制，是导致其具备各向异性的原因。在层状岩体中，隧道开挖后围岩的形变机制是较为复杂的，特别是其处于地质赋存条件与复杂地应力条件时，其破坏模式与破坏机制受软弱面的影响更为显著[1-2]，围岩的稳定性控制面临着较大的挑战。

一些学者对层状岩体的破坏特征、数值分析模型等展开了理论与试验研究。Xu 等[3]采用室内三轴压缩试验，基于声发射、电镜扫描等测试手段对碳质千枚岩的力学特性进行了研究。王章琼等[4]对鄂西北片岩单轴压缩条件下的形变各向异性及水敏特性进行了分析。邓华峰等[5]对单轴与三轴压缩条件下层状砂岩破坏模式的各向异性特征进行了分析。Cho等[6]采用单轴压缩和巴西劈裂试验，得到了片麻岩、页岩和片岩的各向异性特性。吴章雷[7]通过现场原位试验，描述了粉砂质板岩各向异性特征。夏彬伟[8]通过物理模拟试验的方法得出了层状岩体在隧道开挖后的变形特征。吴渤[9]建立了层状岩体弹塑性各向异性力学模型，对层状岩体隧道围岩扰动区演化与锚固机理进行了研究。Xu[10]等通过耦合有限差分-离散元法，研究了层状岩体在隧道开挖后细观角度的力学损伤机理。黎立云等[11]通过断裂力学与有限元方法，对层状岩体断裂破坏的现象与力学机制进行了分析。张春生等[12]基于离散元数值模型，对石英云母片岩各向异性特征的多尺度效应进行了精细化的分析。左双英等[13]将层状岩体的破坏模型分成5种，建立了基于弥散分析方法的岩石各向异性本构模型，并将其用于地下结构围岩的破坏模式分析中。黄书岭等[14]建立了考虑结构面特性的层状岩体复合材料模型。王启耀等[15]全面总结了倾斜层状岩体的力学特征和数值模拟方法,并对各种模拟方法的优缺点进行了比较。王伟等[16]研究了软硬相接岩层分布对隧道围岩稳定性的影响，在卸荷岩体力学理论基础上，考虑了6结构面倾角情况并进行了数值模拟分析。李林毅等[17]研究了单层衬砌结构力学特征，采用FLAC3D有限差分软件，利用软件内置的接触面单元对不同结构层的层间接触效应进行了模拟。

从上述分析可以看出，目前对于层状岩体的研究，多只考虑1组软弱结构面，即层理面的作用。而实际工程中，岩体的赋存条件较为复杂，往往存在着多组优势结构面的共同作用。因此，建立多弱面作用下层状岩体的力学本构模型具有重要的工程意义。本研究基于层理面弥散处理法(即力学模型中岩体仅受层面控制且具备各相异性的连续体)，建立层状岩体双弱面本构模型；采用该模型，对双弱面层状地层中围岩的破坏模式进行系统分析。

1 双弱面层状岩体本构模型

1.1 简化模型

图1(a)中，层理面等作为最发育的结构面在实际的地质体中占据主导地位，此外也还有大量无序节理面发育。其中，优势结构面由于具有明显的方向性，其对岩体的力学特性影响较大；而无序分布的节理面由于其随机性，可以将其作用等效于岩石基质体中，则岩体的力学模型就可以简化为图1(b)。

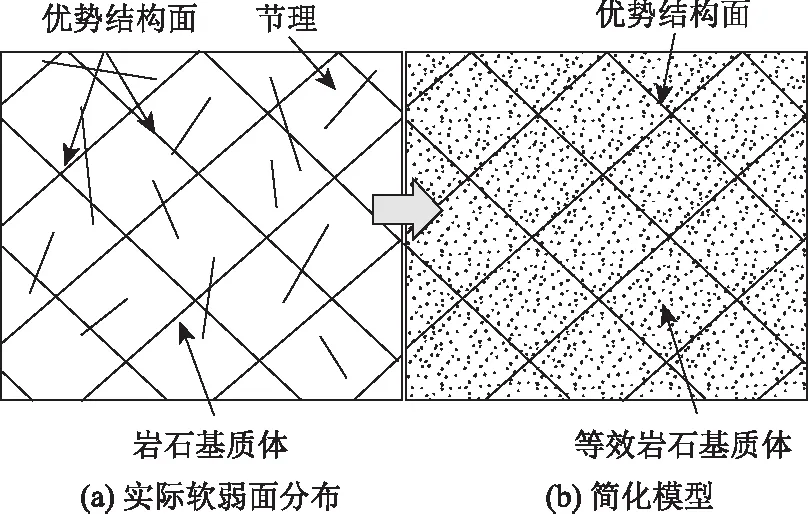
图1 双弱面层状岩体力学模型Fig.1 Mechanical model of double-weak-plane layered rock mass

本研究需推导的模型应满足以下强度和形变条件：

(1)在宏观层面，层状岩体的构成应仅为岩石基质体和层面(结构面)，软弱结构面和岩石基质体均独立考虑其强度特性，并且二者都必须符合带拉伸截断条件下的摩尔-库伦强度准则。

(2)必须满足横观各向同性理论。

1.2 弹性本构关系

模型中针对各组弱面都应设置以方位角和层面倾角为坐标轴的独立坐标系。这些弱面可以任意正交或斜交，并根据实际岩体结构特征设置弱面的分布特性。

由横观各向同性理论可知，局部坐标系(x′,y′,z′，图2) 下，层状各向异性弹性矩阵为：

图2 软弱结构面坐标Fig.2 Coordinates of weak structural plane

(1)

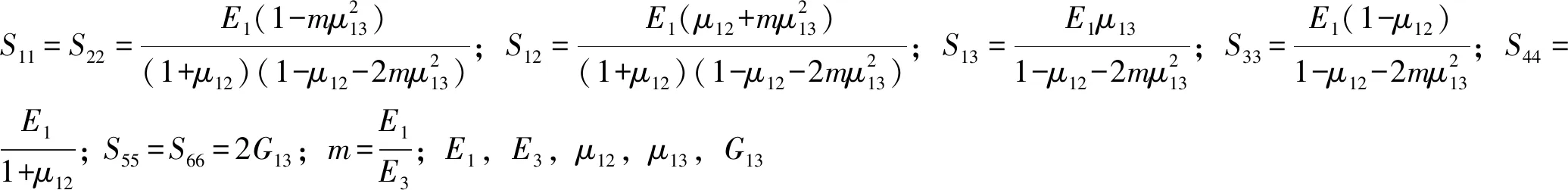
应力转换矩阵为：

R=

(2)

式中li，mi，ni(i=1, 2, 3)为下列矩阵的元素：

Q=

(3)

因此，可得到整体坐标系下应力应变关系为：

σ=RTSP′Rε。

(4)

式中，σ为应力矩阵；ε为应变矩阵。

可知，整体坐标系下的弹性矩阵为:

S=RTS′R，

(5)

式中S为6阶矩阵，其分量记为Cij。

塑性应变增量通过塑性势函数获得，即：

(6)

式中λ，g和σ分别为基岩(或层面)的塑性指示因子、塑性势函数和应力。

其总应变增量表达式：

Δε=Δεp+Δεe,

(7)

式中εe为弹性应变增量。

1.3 屈服准则

在力学性质方面，本研究模型将遵循带拉伸截断的Mohr-Coulomb准则进行岩石基质体与层理面的描述。其中，岩石基质体屈服准则为：

(8)

ft=σt-σ3，

(9)

式中，fs和ft分别为剪切和拉伸屈服法则的表达式；σ1和σ3分别为最大、最小主应力；Nφ=(1+sinφ)/(1-sinφ)；σt，φ，c分别为岩石基质体的抗拉破坏强度、内摩擦角、黏聚力。

相应的势函数为：

gs=σ1-σ3Nψ,

(10)

gt=-σ3,

(11)

式中，gs为剪切势函数；gt为拉伸势函数，Nψ=(1+sinψ)/(1-sinψ)，ψ为岩石的剪胀角。

软弱面的屈服准则为：

(12)

(13)

(14)

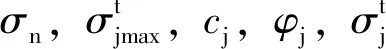
对应的塑性势函数为：

(15)

(16)

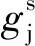
1.4 塑性修正

FLAC3D中，本构模型二次开发最重要的步骤就是要对单元体进行塑性应力修正。根据其手册中提出的推导建议，双弱面模型塑性应力修正表达式如下。

当岩石的基质体发生剪切破坏时，

(17)

式中，σN和τN分别为修正后的法相应力和切向应力各分量值；σI和τI分别为修正前的法相应力和切向应力各分量值，且修正参数λs为：

(18)

当发生拉伸破坏时,

(19)

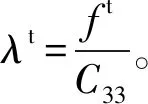
对于软弱面而言，当发生剪切破坏时,

(20)

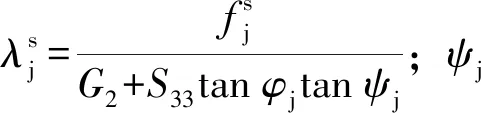
当发生拉伸破坏时,

(21)

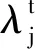
图3为通过C++语言对上述研究模型开展的二次开发流程。

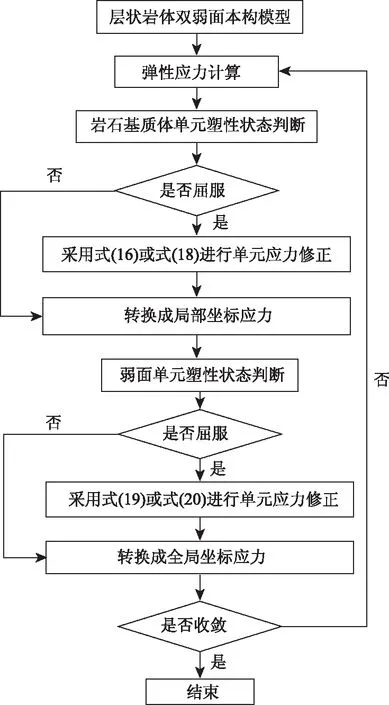
图3 模型开发流程图Fig.3 Flowchart of model development

1.5 参数反演流程

由于模型参数众多，准确快速地确定模型中各参数的取值是模型应用的关键。根据室内试验结果，本研究采用的参数标定过程如下。

1.5.1形变参数标定

(1)选取层理面弹性模量对试样弹性模量影响最小的加载角度标定岩石基质体的弹性模量。

(2)选取层理面弹性模量对试样弹性模量影响最大的加载角度标定层理面的弹性模量。

1.5.2强度参数的标定

(1)选取层理面强度对试样强度影响最小的加载角度标定岩石基质体的强度。

(2)根据各个角度下的抗压强度值，对层理面的强度参数进行标定，将数值结果与试验结果综合比对，选取最为合理的强度值。

2 模型验证

2.1 单弱面层状岩体试验验证

目前层状岩石力学特性的室内试验研究均针对单一弱面结构。因此，本节进行模型验证时，也只考虑1组层面的作用(用模型中的开关函数，忽略另1组层理面的作用) 。试验数据来源于Konietzky 内单轴压缩试验结果[18]。建立的单轴压缩数值模型如图4所示。模型为圆柱体形状，高10 cm，半径2.5 cm，各层理之间相隔1 cm，模型底面设置轴向约束，侧面和顶面不设置约束，并在模型上表面以1×10-7m/s的法向速度进行加载试验。

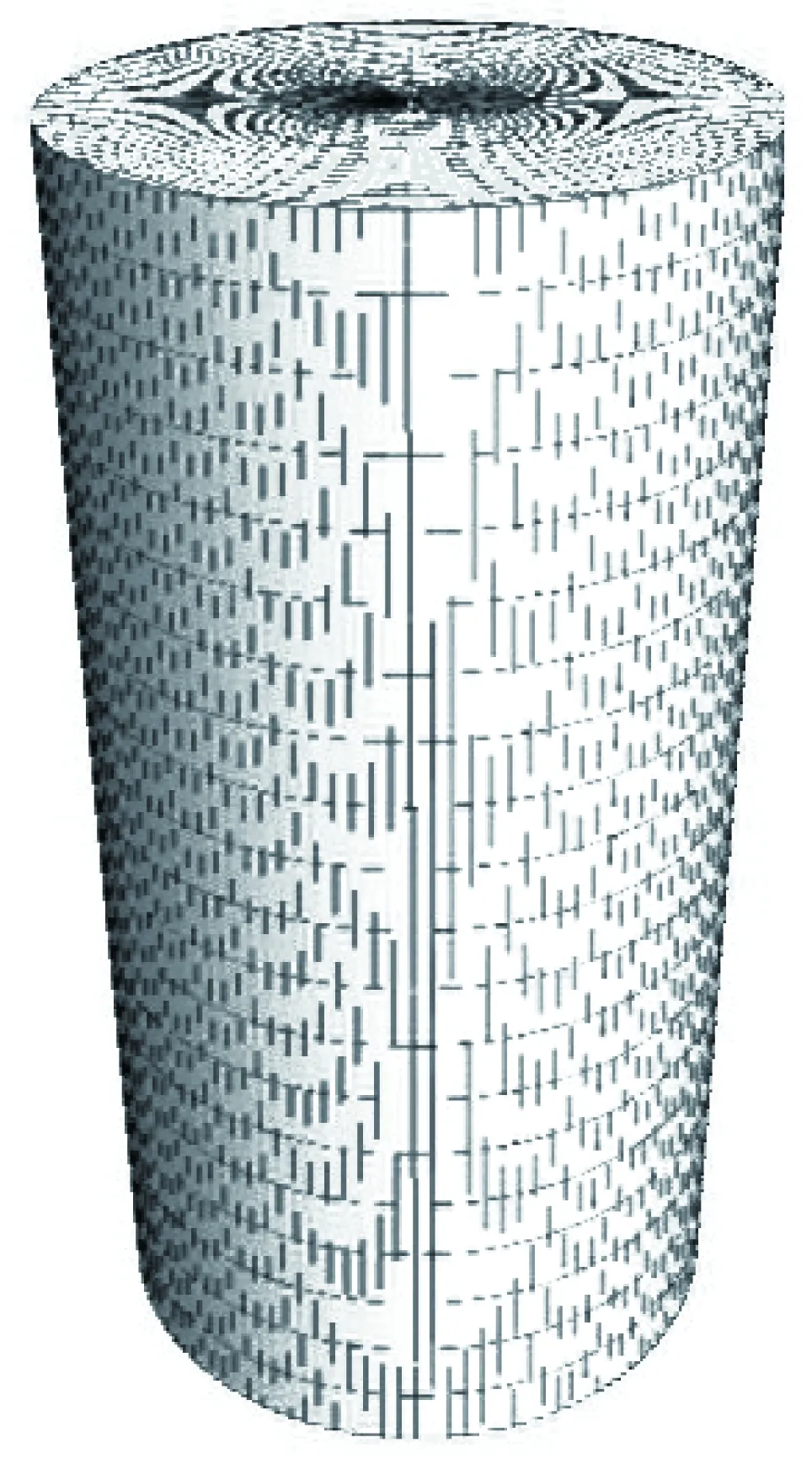
图4 数值计算的单轴压缩试验模型Fig.4 Uniaxial compression test model of numerical calculation

数值计算模型中各材料的力学参数详见表1，数值计算结果如图5所示，数值模拟与试验试样结果吻合较好。从图5(a)可以看出，试样角度层理面的倾角θ与强度值之间的关系呈U型分布，最小值在θ=60°时取得，最大值在θ=90°时取得。从图5(b)可以看出，当θ=0°时，岩样产生剪切破坏，此时层理面对岩样的破坏模式影响较小；当θ=30°与60°时，岩样产生沿层理面的剪切破坏；当θ=90°时，岩样产生多个沿着层理面的劈裂破坏。

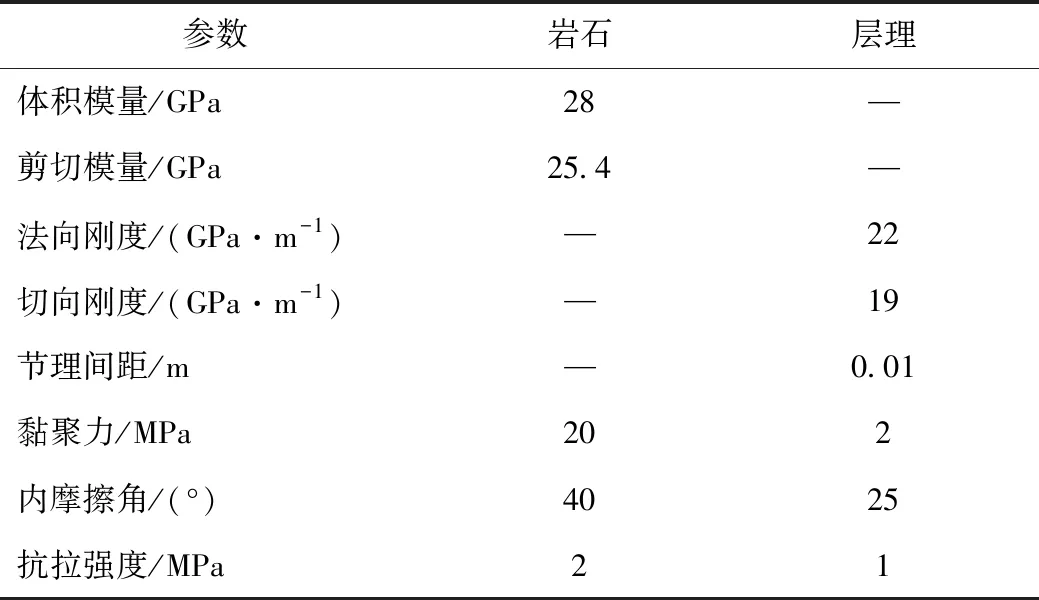
表1 参数Tab.1 Parameters

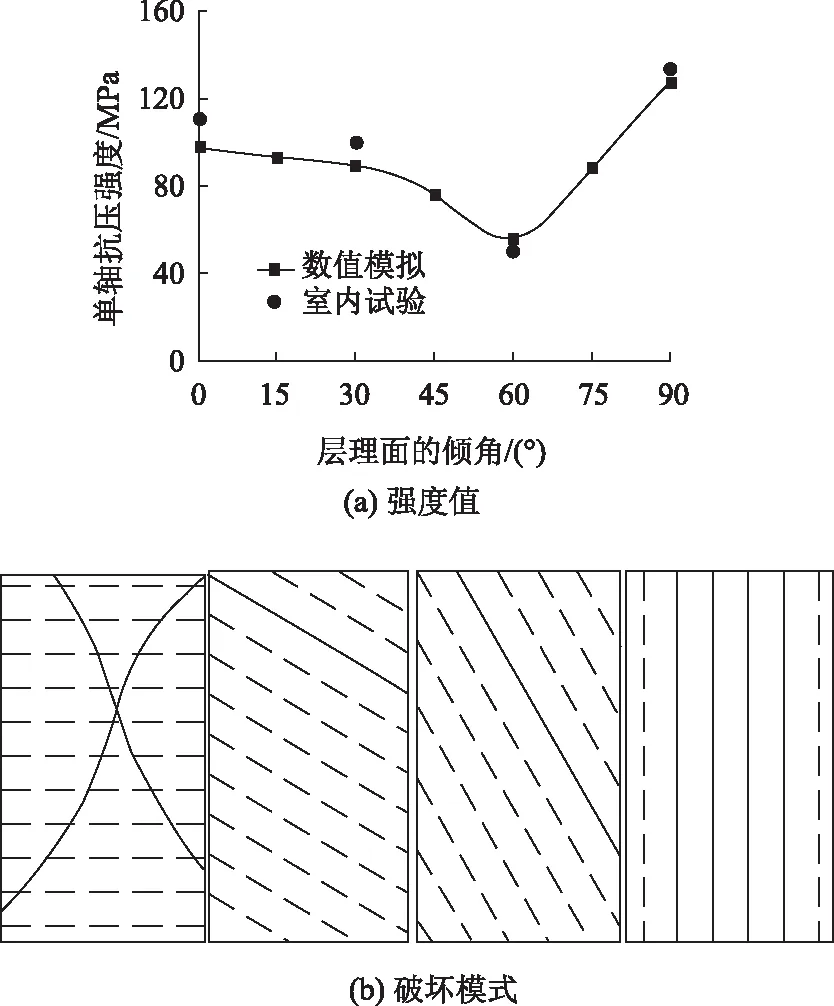
图5 计算结果与室内试验对比Fig.5 Comparison between calculated result and laboratory test

2.2 双弱面层状岩石单轴压缩数值试验

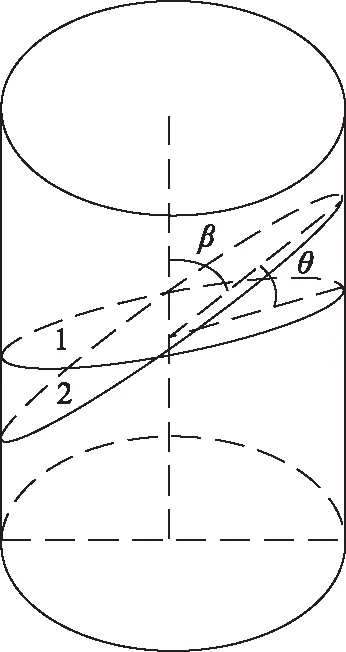
图6 双弱面层状岩体示意图Fig.6 Schematic diagram of rock mass with double-weak-plane

双弱面层状岩石间层理面夹角的几何关系如图6所示。其中，弱面2与竖向夹角为β，两弱面之间的夹角为θ。本算例中，取θ=30°，β=0°～90°。每个弱面方向层理面间距为1 cm。

图7为计算得到的岩石单轴抗压强度与β的关系。可以看出，当β=0°时，弱面2平行于外力方向，弱面1与外力方向的夹角为30°，岩石的单轴抗压强度最小；当β=30°时，弱面1与外力方向的夹角为60°，岩石的单轴抗压强度略大于β=0°工况；当β=60°时，弱面1与外力方向垂直，岩石的单轴抗压强度最大。可以发现，当两个弱面中有1个弱面与外力方向的夹角为30°时，岩石的单轴抗压强度最小。

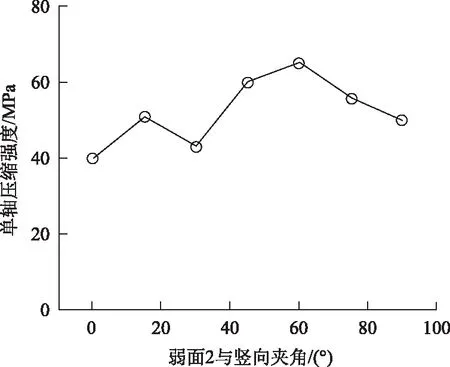
图7 单轴抗压强度与β的关系Fig.7 Relationship between uniaxial compressive strength and β

2.3 单弱面层状岩石隧道开挖稳定性

为了验证模型的开挖效应，采用本研究的本构模型对单软弱层面的层状岩体在隧道开挖后的非对称性破坏特性进行描述。建立图8所示的计算模型，层理面倾角(层理面与隧道x轴正向夹角)为0°，45°，90°。模型为平面应变模型，隧道中心与其左右、上下边界的距离均为40 m。除模型底部边界外，将其余边界均设置为法向应力边界，而底部边界约束竖向位移。采用在开挖边界上施加与节点不平衡力相反方向的节点力来实现地应力的释放。地应力场为均匀地应力场，即σx=σy=σz=15 MPa。围岩的力学参数如表1所示。

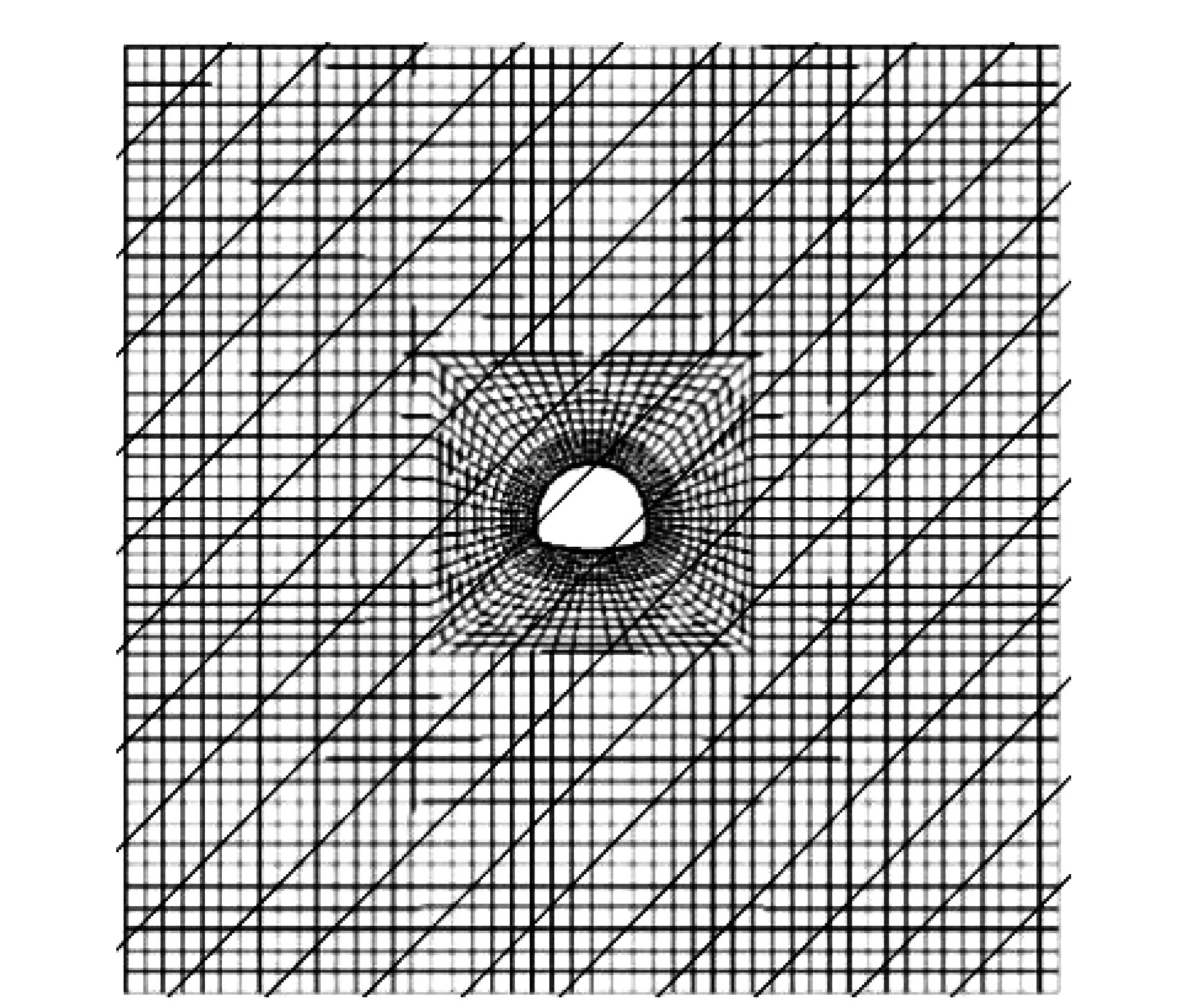
图8 计算模型Fig.8 Calculation model

计算结果如图9所示。可以看出，当层理面倾角为0°或90°时，由于岩体结构对称分布，围岩的破坏区也对称分布。对于0°而言，其拱顶与拱底区域的岩石由于层理面的弯折效应，塑性区分布范围略大于拱腰；而对于90°而言，其拱腰区域的岩石由于层理面的弯折效应，塑性区略大于拱顶与拱底。当层理面倾角为45°时，围岩的破坏区体现出强烈的非对称分布特性。同时，左拱肩处岩体破坏最为严重，与实际工程观察到的结果相似(图9)。

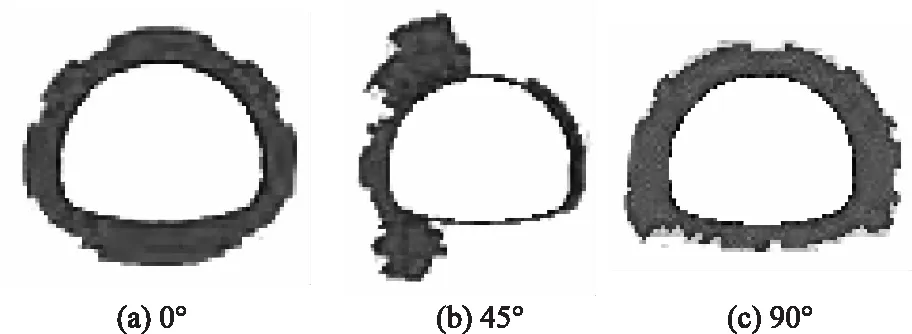
图9 围岩破坏区Fig.9 Failure zones of surrounding rock

3 隧道开挖稳定性分析

3.1 数值模型

选取3种地应力场(均匀地应力场、竖向和水平构造应力场为主的应力场)研究层状岩体双弱面不同组合下隧道开挖后围岩的破坏特征，其应力值分别为：σx=σy=σz=15 MPa，σx=σy=10 MPa，σz=15 MPa；σx=σy=15 MPa，σz=10 MPa。各种地应力场下计算工况如表2所示，围岩及层理面的力学参数如表1所示，计算模型如图8所示。其中，层理面倾角为层理面与隧道x轴正向夹角，层理面倾向为层理面与隧道轴线之间的夹角。

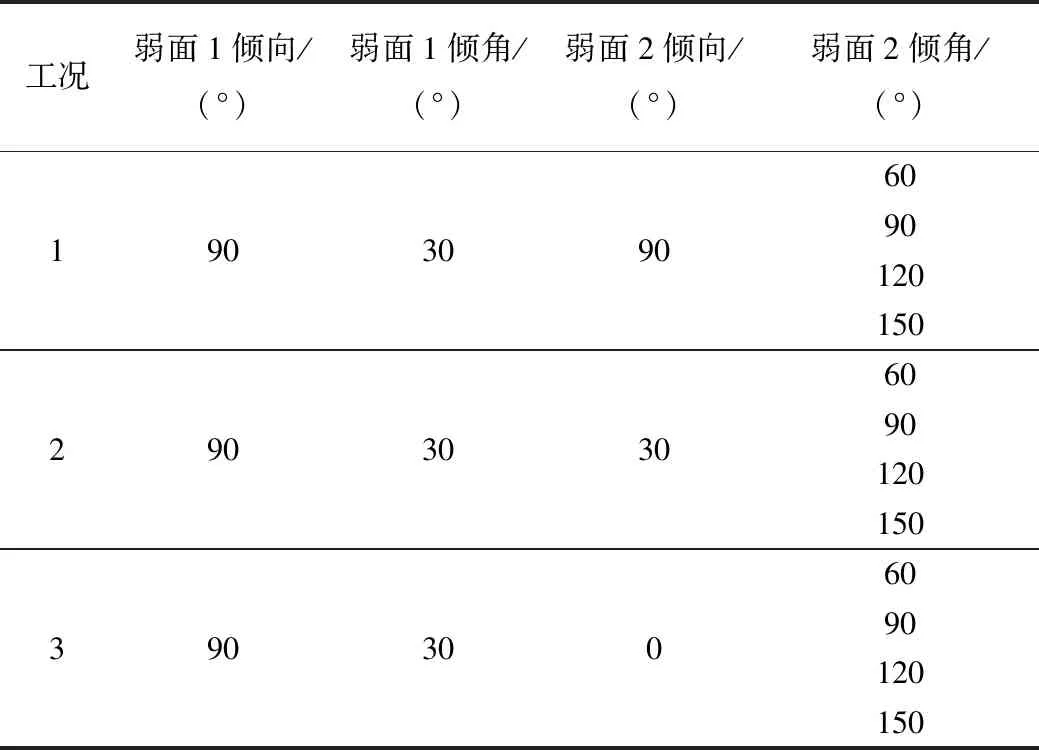
表2 计算工况Tab.2 Calculating conditions

3.2 双弱面空间组合方式的影响

在应力场为σx=σy=σz=15 MPa的均匀地应力场条件下，双软弱层面在各类产状的平行试验结果(隧道开挖后围岩破坏特征)如图10～图12所示。由于计算中弱面1的倾向与倾角不变，因此，对于每种组合，可以以弱面2的倾向与倾角简称，如组合90-60为弱面2倾向为90°、倾角为60°的工况。

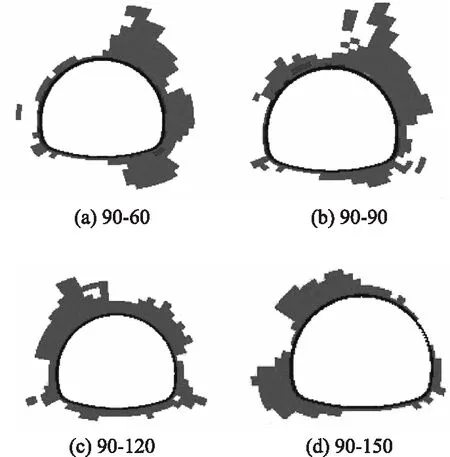
图10 工况1围岩塑性破坏区分布Fig.10 Distribution of plastic failure zones of surrounding rock under working condition 1

从图10可以看出，对于组合90-60而言，围岩的塑性破坏区集中分布在隧道的右侧，且右拱肩与右拱脚附近围岩的破坏最为严重；对于组合90-90而言，围岩的塑性破坏区主要分布在隧道的右拱肩附近，且左拱肩与右拱脚附近围岩也在一定范围内产生了损伤；对于组合90-120而言，围岩的塑性破坏集中分布在隧道起拱线上侧洞周附近的岩体处，且左拱肩破坏最为严重；对于组合90-150而言，隧道开挖后围岩的破坏主要集中于隧道左侧拱肩和拱脚附近(塑性破坏区)。

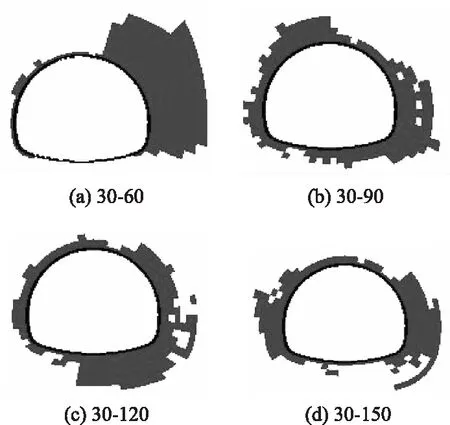
图11 工况2围岩塑性破坏区分布Fig.11 Distribution of plastic failure zones of surrounding rock under working condition 2

从图11可以看出，对于组合30-60而言，围岩的塑性破坏集中分布在隧道右侧拱顶至拱脚附近，体现出极强的非对称破坏特征；对于组合30-90而言，围岩的塑性破坏集中分布在隧道左拱肩与右拱腰附近；对于组合30-120而言，围岩的塑性破坏集中分布在隧道拱底至右拱肩范围内，且隧道拱底的塑性破坏最为严重；对于组合30-150而言，围岩的塑性破坏区较为对称地分布在隧道左右拱腰两侧，且右侧围岩的破坏区范围略大于左侧。

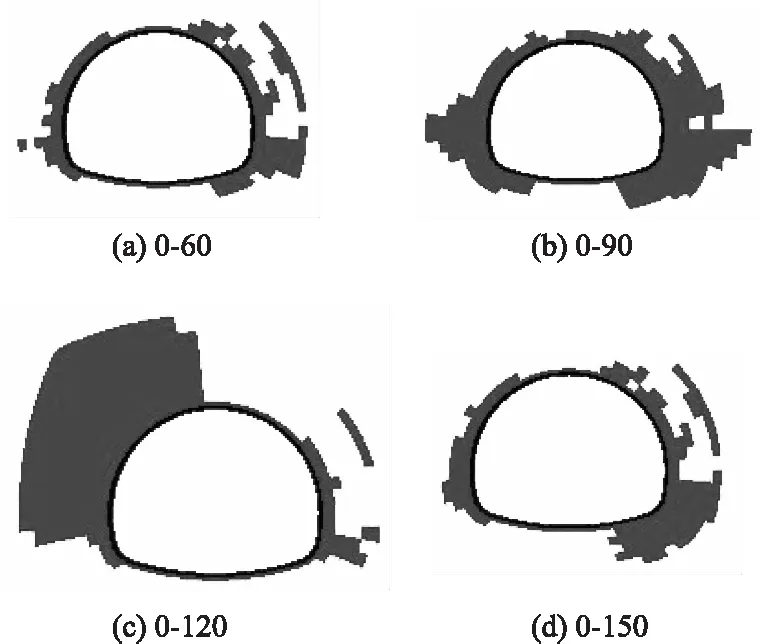
图12 工况3 围岩塑性破坏区分布Fig.12 Distribution of plastic failure zones of surrounding rock under working condition 3

从图12可以看出，对于组合0-60而言，围岩的塑性破坏主要集中在右拱脚附近；对于组合0-90而言，围岩的塑性破坏区域在隧道左右两侧分布较为均匀，且主要集中在左右拱腰附近；对于0-120而言，围岩的塑性破坏集中分布在隧道拱顶至左拱腰附近，体现出极强的非对称性；对于0-150而言，围岩的塑性破坏区域主要集中在右拱脚附近，破坏形态与组合0-60相似。

对比图10～图12可以看出，双软弱面围岩中弱面间的倾向与倾角的组合对围岩破坏模式有很大影响，多数情况下均体现出明显的非对称破坏特征。

3.3 地应力场的影响

以工况1为例，分析地应力场对围岩破坏模式的影响。图13、图14分别为侧压力系数λ=σy/σx>1与λ<1时时围岩的塑性区分布。与图10对比可以看出，对于不同构造应力场条件下的相同组合而言，随着弱面2倾角的增加，围岩破坏模式之间的差异逐渐增大。当组合为90-60时，不同地应力场条件下的围岩破坏区域相似，只是破坏程度有所差异；而当组合为90-150时，围岩破坏形态之间的差异很大，λ<1时围岩破坏区域集中分布在左拱脚附近；λ>1时在隧道拱腰两侧对称分布；λ=1时集中分布在左拱肩与左拱腰附近。

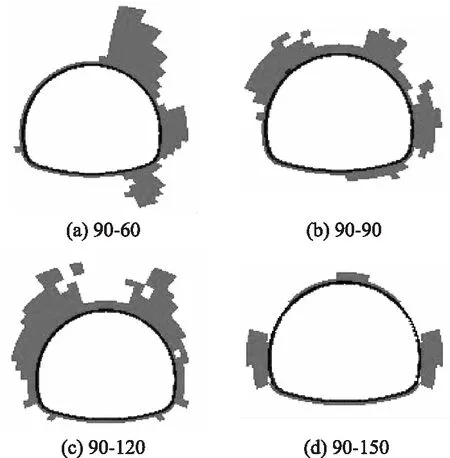
图13 工况1围岩塑性破坏区分布(λ>1)Fig.13 Distribution of plastic failure zones of surrounding rock under working condition 1(λ>1)

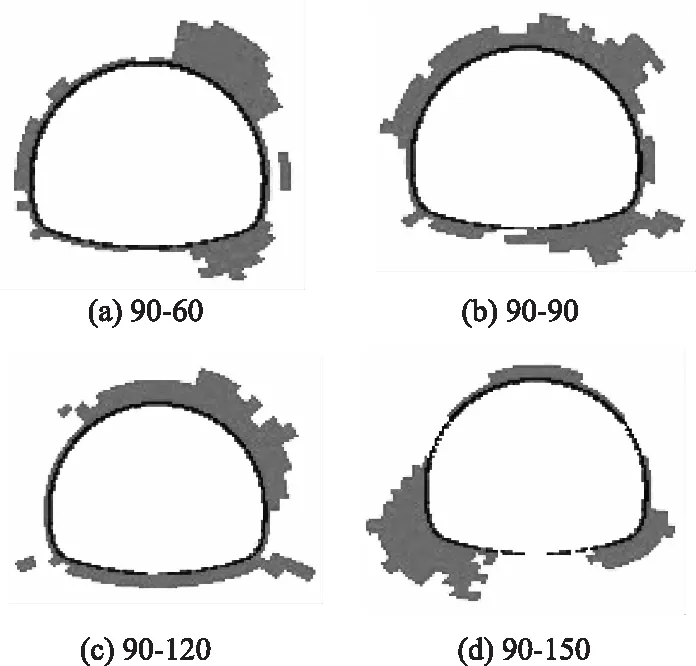
图14 工况1围岩塑性破坏区分布(λ<1)Fig.14 Distribution of plastic failure zones of surrounding rock under working condition 1(λ<1)

可以看出，对于双弱面层状岩体而言，围岩的破坏模式受到弱面的空间形态与地应力场的共同控制，大多数情况下均体现出明显的非对称破坏特征。因此在实际工程中，要根据岩体弱面的实际组合，找出围岩的关键破坏位置，然后进行针对性的加强支护来控制围岩的非对称变形。

4 结论

本研究基于层理面的弥散处理方法，建立了层状岩体双弱面本构模型。采用该模型，对双弱面层状地层中围岩的破坏模式进行了系统分析，得到以下结论：

(1)岩石强度、形变与破坏形式的各项异性特征可以通过开发的双弱面模型很好地表现。

(2)双软弱面围岩中弱面间的倾向与倾角的组合对围岩的破坏模式有很大的影响，大多数情况下均体现出明显的非对称破坏特征。

(3)对于不同构造应力场条件下的相同组合而言，随着弱面倾角的增加，围岩破坏模式之间的差异逐渐增大。

隧道的开挖是一个卸荷过程，因此，下一步应该从室内试验与数值模拟两个方面对双弱面层状岩石的卸荷力学特性进行研究；同时，基于双弱面层状岩体中隧道开挖的围岩破坏形态，可以进行针对性的非对称形变控制措施研究。