关于费耶算子逼近定理的一种简化证明
高 义
(北方民族大学数学与信息科学学院,宁夏银川 750021)
0 引言
一个周期为2π且连续的函数f(x),在它的连续点x0,并不能保证其傅立叶级数收敛到f(x0).为此,数学教材[1]在讨论傅立叶级数的收敛性时引进了费耶算子(亦称费耶和,1904年由匈牙利数学家费耶首次提出):
(1)
其中f(x)∈C2π,C2π表示以2π为周期的连续函数全体.该算子可以弥补某个连续函数f(x)的傅立叶级数未必收敛到f(x)的缺憾.事实上,费耶算子是傅立叶级数部分和的算术平均.为方便读者,本文将费耶算子由傅立叶级数部分和的算术平均生成的推导过程重复如下(细节可参考文献[1]).若f(x)∈C2π,则f(x)可以展开成傅立叶级数(本文只讨论连续函数的情形,事实上,只要f(x)在[-π,π]绝对可积亦可以展开成傅立叶级数),即
其中
若傅立叶级数的部分和记作
将ak,bk代入到Sn(f;x)中,得
(2)
注意到
(3)
则函数f(x)的傅立叶和为
(4)
为此,定义费耶和为
(5)
由式(4),得
注意到
(6)
则费耶和可以写作为式(1)的形式.
若记
不难得到
人们称Dn(x)为狄利克雷核,Kn(x)为费耶核.从卷积[2]的观点看,傅立叶和是f(x)与Dn(x)的卷积,而费耶算子是f(x)与Kn(x)的卷积.教材[1]用分析的方法证明了费耶算子的逼近定理,即如下的定理.
定理1若f(x)∈C2π,则
即费耶算子σn(f;x)在实轴上一致收敛于f(x),其中
本文利用柯罗夫金定理[3]给出定理1的另外一种简化的证明.
1 准备知识
为证明定理1,需作如下的准备知识.
定义1[4]假设L是映某个函数空间S到自身的映照,如果它将S中每一个正的元素都映照为正的元素,那么说L是一个正算子.另外,如果对于S中的任意两个元素f1和f2以及实数α,β∈,有
L(αf1+βf2)=αL(f1)+βL(f2),
则称L是一个线性正算子.
容易验证σn(f;x)是C2π到其自身的线性正算子.
定理2[3](柯罗夫金定理)设Ln(f;x)是C2π上的线性正算子序列,下列三条件满足:
Ln(1;x)=1+αn(x),
Ln(cost;x)=cosx+βn(x),
Ln(sint;x)=sinx+γn(x),
其中αn(x),βn(x),γn(x)在全实轴上一致收敛于零,那么对于任一f(x)∈C2π,Ln(f;x)在全实轴上也一致收敛于f(x).
2 定理的证明
为证明定理1,根据柯罗夫金定理,只需证明σn(1;x),σn(cost;x),σn(sint;x)在全实轴上分别一致收敛于1, cosx, sinx即可.
引理1设σn(f;x)是费耶算子,则
(i)σn(1;x)=1,
证明:(i)注意到Sk(1;x)=1,k=0,1,2,...,n,由式(5),不难得到
下证明(ii)和(iii).结合式(3)和(6),有
因此根据三角函数系的正交性,得
同理,有
定理3σn(fk;x)在全实轴上分别一致收敛于fk(x),k=0,1,2,
其中f0(x)=1,f1(x)=cosx,f2(x)=sinx.
证明:由引理1即得.
定理1的成功证明意味着魏尔斯特拉斯第二定理的获证,即为证明魏尔斯特拉斯第二定理提供了一种构造性的证明方法,所以定理1的意义非同寻常.这里,将魏尔斯特拉斯第二定理也写出.
定理4[4,5]若f(x)∈C2π,则对于任意给定的正数ε,都存在三角多项式t(x)满足不等式
‖f-t‖C2π<ε.
再回到傅立叶级数收敛性的问题上,尽管f(x)的傅立叶和Sn(f;x)在其连续点上未必收敛到f(x),但文献[4]给出了Sn(f;x)逼近f(x)最坏情况的估计.
定理5[4]若f(x)∈C2π,则
‖Sn(f)-f‖C2π

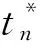
定理5说明较傅立叶和逼近连续函数时,费耶算子逼近连续函数的性能更佳.关于二者更加精细的逼近刻画可参见文献[4].
3 结论
本文在引进线性正算子定义的基础上,首先说明费耶算子是正线性算子.其次借助柯罗夫金定理证明费耶算子在全实轴上一致收敛.最后,以傅立叶和的逼近度展示了费耶算子在逼近连续函数的优越性.

