一类Frobenius图网络

蔡晓霞,孔祥志,王 燕

(烟台大学数学与信息科学学院,山东 烟台 264005)

1 引言与预备知识

在近代图论的发展中,随着计算机网络的诞生和发展,用图来模拟网络是研究和开发网络的一个重要手段,凯莱图因其天生的对称性吸引了许多图论学家的注意,在过去的几十年中涌现出来许多好的凯莱图网络模型.

定义1[1]假设G是一个群,S⊆G且同时满足以下条件:单位元e∉S;对∀a∈S,有a-1∈S;G=,则称S是G的一个凯莱子集.

定义2[1]假设G是一个群,S是G的一个凯莱子集,构造凯莱图Γ如下:Γ的顶点为G中所有的元素;对于任意的a,b∈G,a与b在Γ中有连边当且仅当存在x∈S,有b=a·x,并记Γ=Cay(G,S).

定义3[2]设K和H为2个群,若φ为H到Aut(K)内的同态映射,则称φ为H在K上的一个作用.根据半直积理论,φ可以唯一确定一个K和H的半直积[K]H.特别地,如果H在K{1K}上的作用是半正则的(无不动点),就称群G=[K]H为Frobenius群,称K为这个群的Frobenius核,H为一个Frobenius补.

定义4[3]假设G是集合Ω上的一个置换群,则G在集合Ω×Ω上诱导了一个作用:任取(x,y)∈Ω×Ω,g∈G,都有(x,y)g=(xg,yg).如果G在Ω上作用是传递的,则把G在Ω×Ω上作用的轨道称为轨道类(orbital). 此时集合{(x,x)|x∈Ω}为一个轨道类,称为平凡轨道类;而集合(Ω)2={(x,y)|x,y∈Ω,x≠y}中包含的轨道类称为非平凡的.

定义5[3]令G=[K]H是集合Ω上的一个Frobenius群. 一个图Γ如果以Ω为顶点集,以集合E={{x,y}|(x,y)∈O}为边集合,其中O为(Ω)2中包含的某个轨道类,就称图Γ为一个G-Frobenius图. 如果G的Frobenius核是初等阿贝尔群,那么称Frobenius图Γ是仿射的.

文献[3]中已经证明一个G-Frobenius图是它的核K的凯莱图,相应的凯莱子集是H的一个轨道或者2个互逆轨道的并集.因此,Frobenius图是弧传递(一个轨道时)或者边传递且点传递(2个互逆轨道的并集时).

注1 (1)关于Frobenius图的详细定义和性质请参考文献[3].

(2)本文中提到的关于图的相关定义可以参考文献[1],关于群作用及其传递性的相关定义可以参考文献[4].

2 一类特殊凯莱图

考虑矩阵

显然M∈GL(n,p)≅Aut(K).M固定K的零元. 通过计算可知Mn=αI,因此M生成的子群H=〈M〉为εn阶的循环群. 取e=(1,0,0,…,0)∈K,令集合S=eH≡{eMi|1≤i≤εn}.

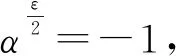
注2如果令集合s={αt|0≤t≤ε-1},那么γ=Cay(Fp,s)就是一个度为ε的循环图,并且Γ是γ的n次笛卡尔积.

下面讨论Γ=Cay(K,S)的哈密尔顿性和连通性.

2.1 哈密尔顿性

定义6如果一个图中的任意两点都被一条哈密尔顿路(经过图中每个点一次且只一次的路)相连接就称该图为哈密尔顿连通的.

引理1[5]假设Γ是一个定义在阿贝尔群上的连通凯莱图.如果val(Γ)=2,则Γ是一个圈;如果val(Γ)>2,那么只要Γ不是二部图,Γ就是哈密尔顿连通的.

定理1 凯莱图Γ=Cay(K,S)是哈密尔顿连通的.

证明根据定义2,Γ是阿贝尔群K上的连通凯莱图.注意到γ=Cay(Fp,s)中有p-圈(0,α,2α,…,(p-1)α,0),因此γ不是一个二部图,从而Γ不是一个二部图. 于是由引理1知Γ是哈密尔顿连通的.

定义7 设Γ为一个度为2k的正则图,如果Γ的边集合E(Γ)可以分划为k个哈密顿圈,则称图Γ为哈密尔顿可分解的.

引理2[6]如果Ci是一个圈,其中1≤i≤n,那么笛卡尔积Γ=C1×C2×…×Cn能够分解为n个哈密尔顿圈.

定理2 上面构造的凯莱图Γ=Cay(K,S)是哈密尔顿可分解的.

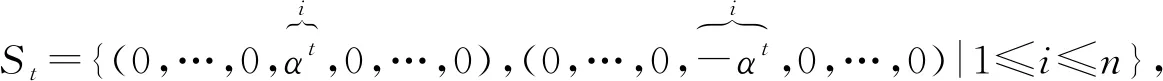
2.2 连通性

定义8 令Γ为一个连通图,用δ(Γ)表示Γ中的最小的度.如果从Γ的边(顶点)集中去掉一个i元子集之后变为一个不连通图或者平凡图,那么就称这个子集为i元的边(点)割集;称最小的边(点)割集的元素个数为边(点)连通度,记为λ(Γ)(κ(Γ)).

定义9 如果一个图Γ满足λ(Γ)=δ(Γ)(κ(Γ)=δ(Γ)),就称图Γ是最大边(点)连通的.

定义10 如果Γ的所有最小边(点)割集都是与一个点相关连的边(点)构成的,那么称Γ为超边(点)连通图.

引理3[7]令Cay(Zn,S)为一个循环图,其中S={±a1,±a2,…,±ak}.如果当aj≥4时,(aj,n)=1,那么Cay(Zn,S)是最大点连通的.

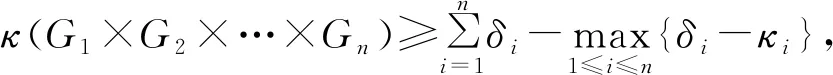
定理3 上面构造的凯莱图Γ=Cay(K,S)是最大点连通的.

证明根据定义,Γ是γ=Cay(Fp,s)的n次笛卡尔积.根据引理3可知γ是最大点连通的,再由引理4可知κ(Γ)≥nm=δ(Γ).根据Whitney不等式κ(Γ)≤δ(Γ),因此κ(Γ)=δ(Γ).

引理5[9]如果k≥2,那么Cay(Zn,{±1,±a2,…,±ak})是超边连通图.

由引理5容易得到γ=Cay(Fp,s)是超边连通的.

引理6[10]给定2个正则且具有最大点连通度的图G1和Γ,用递归的方法定义的图Gn=Gn-1×Γ,n≥2,除了K2×Kn,n≥2之外都是超点和超边连通的.

定理4 上面构造的凯莱图Γ=Cay(K,S)是超点和超边连通的.

证明注意到γ=Cay(Fp,s)满足引理3是最大点连通的正则图. 因为Γ是γ的n次笛卡尔积,满足引理6的条件,因此Γ既是超点连通图也是超边连通图.

3 Frobenius图

下面证明凯莱图Γ=Cay(K,S)在一定条件下还是Frobenius图,这只需证明H在K{0}上作用半正则.

引理7矩阵M在K{0}上作用半正则.

证明令I为n阶单位矩阵,则

假设存在x=(x1,x2,…,xn)∈K{0},但是x(I-M)=0,就可以得到下列方程组:

由假设知,存在k,1≤k≤n,xk≠0,根据方程组的前n-1个方程知x=(xk,…,xk),带入方程组的最后一个方程可得:α=1,这与o(α)=ε为偶数阶矛盾.

因此,任意的x=(x1,x2,…,xn)∈K{0},都有x(I-M)≠0,这说明1不是M的特征值,所以M在K上除零元外是无不动点的,即M在K{0}上作用半正则.

定理5如果pi|ε,i=1，…,r,那么H在K{0}上的作用是半正则的.

证明假设有y=(y1,…,yn)≠0使得Hy≠{e}.那么就存在正整数j|nε且j1.因为gcd(k,l)=1,l=ε,,所以gcd(ε,k)=1.

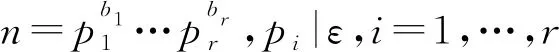
证明由定理5可知[K]H是一个Frobenius群,因此Γ是一个仿射的Frobenius图.