含水层饱和砂土蠕变试验及流变模型辨识研究
杨伟涛,徐 进,王少伟
(烟台大学土木工程学院,山东 烟台264005)
含水层抽水引起地下水位降低,导致含水层土体骨架承受的有效应力增加,致使含水层固结压密,弱透水层释水变形,从而引起地面沉降,抽水引起的地面沉降包括含水层变形和弱透水层变形两部分[1].传统观念认为在地面沉降中含水层砂土的贡献可以忽略不计,地面沉降主要是由弱透水层的压缩变形引起,而且弱透水层黏性土的蠕变是导致地面沉降长期发展的主要原因[2-5].然而,近些年对于地面沉降的进一步研究发现,当含水层厚度较大时,地面沉降中砂性土的变形也占有一定的比例,甚至与弱透水层变形量相当[6-9].同时,由于颗粒重组和颗粒破碎等机理,砂土也具有蠕变变形特征[10].因此,通过试验找出合适的流变模型来描述含水层砂土的蠕变特性,对于地面沉降长期变形的精确预测具有重要的理论意义.
目前多采用经验流变模型和理论流变模型来描述土体的流变性[7,10].经验模型主要是在蠕变,应力松弛和恒应变率这些拟合试验结果的基础上得到[10].近年来,随着对土体流变特性的不断深入研究,各种经验模型在一些地区的含水层土体蠕变研究中得到了很好的应用.王艳芳等[11]利用室内改装的应力控制式三轴仪对河北唐山京唐港饱和砂土进行排水蠕变特性研究,发现在应力水平不超过0.8的情况下,Mesri经验模型对该地区砂土的蠕变规律拟合效果较好.王非等[12]利用常州和上海的地面沉降实测数据验证了用Singh经验模型计算含水层变形的有效性.经验模型容易求取、应用方便,但是由于缺乏物理意义,普适性较差,也不便于数值应用[10,13].
理论流变模型借助力学元件来模拟土体的弹性和黏性变形,概念直观,物理意义明确,可以直接代入数值计算用于地面沉降预测[13-14].施小清等[6]对常州含水层饱和砂性土进行单轴压缩试验,从Merchant体、Burgers体2个流变模型中识别出Burgers体能够更好地描述该地区含水层砂土的流变性.杨奇等[15]用三单元Merchant体和四单元Schiffman体较好地描述了桩底砂土层的蠕变变形特性.孙晓涵等[16]运用自行研制的高压固结仪,选取了西安市含水层具有代表性的中细砂样进行研究,提出了适合于西安地区含水层蠕变特性的广义Kelvin体.不同地区土体流变特性迥异,流变本构模型又形式多样.因此,除了参数反演,流变本构模型本身的反演问题(即如何根据实测资料辨识出最佳的流变模型)也同样重要[14].目前关于砂土流变特性的研究中,多是基于给定的一种或2种流变模型进行参数反演,从更广泛的流变模型中识别筛选出最优模型的相关研究仍然较少[15-18].
为此,本文选取长三角地面沉降区饱和砂性土进行单轴压缩试验,验证了砂性土具有蠕变特征并基于试验现象与结果,从Merchant体、开尔文体(K)、广义开尔文体(H-K)、Burgers体、饱依丁-汤姆逊体(H-M)5个能表征衰减蠕变的流变模型中识别出最优的理论流变模型,以便能够更好地描述含水层饱和砂性土的流变特性,为后续的地面沉降理论计算和数值分析做参考.
1 单轴蠕变试验
土样是选自长三角地面沉降区的饱和砂性土,利用环刀进行取样,试样高20 cm,面积为30 cm2,各项物理指标如表1所示.通过单轴高压固结仪,对试样进行室内高压固结试验,采用梯度加载法,加载比为3.设置了2组试验,如图1所示,分别在图中左右2台仪器中进行试验,通过2组试验的数据对比确保试验操作流程没有出现失误而导致数据失真.每级荷载施加后数据的读取按照1 min、10 min、15 min、20 min、30 min、45 min、1 h、2 h、4 h、8 h、12 h、23 h、1 d、2 d(后期每隔一天读取一次)的时间间隔直至变形稳定,当变形量小于0.005 mm/d时视为变形稳定.起始压力和最大压力分别为50 kPa和3 200 kPa,试验过程中温度始终保持在(23±3) ℃.

表1 饱和砂土的各项物理力学性质指标

图1 分级荷载下蠕变试验
2 试验结果与分析
通过2组试验数据对比发现其变形值近乎一致,表明试验未出现不当操作.选其中一组试样,该试样各级荷载作用下的蠕变曲线如图2所示,从图中可以发现蠕变曲线具有明显的阶段性.第一阶段为衰减蠕变过程,即加载初期变形随着时间的增加而增加,但相同时间增量内变形增量逐渐减小,最终变形趋向于与荷载有关的某个定值[19-20].第二阶段即在加载后期变形继续增加,但变形速率基本保持不变,这是由于在室内高压固结试验中,试样受到了来自环刀的侧向约束,在轴向应力下土样不断被挤压密实,强度也因此不断提高,故没有出现因变形快速增加而导致试样被破坏的现象[19].
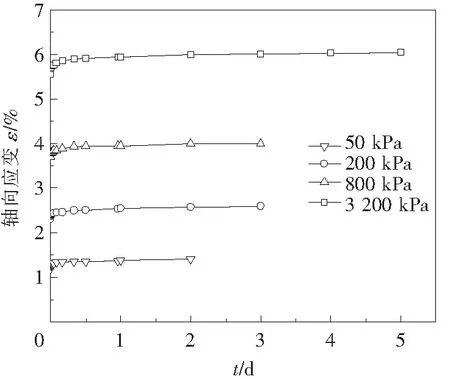
图2 各级荷载下的蠕变曲线
将蠕变变形与时间的关系表示在双对数坐标系中如图3所示,从图中可以发现在双对数坐标系中蠕变变形与时间具有很好的线性关系,但也能看出其具有阶段性,如在50 kPa和3 200 kPa下的曲线,可以很明显地发现在2 h附近出现了转折点.这是由于在荷载作用下,土体的沉降包括三部分,分别是瞬时沉降、固结沉降和次固结沉降[21].因为砂性土的透水性极强,固结沉降完成快,导致瞬时沉降与固结沉降已分不开.因此,前2种沉降完成的快,在后期变形中主要是次固结沉降即蠕变变形,所以该转折点所对应的时间可以看成是固结完成的时间[21-22].
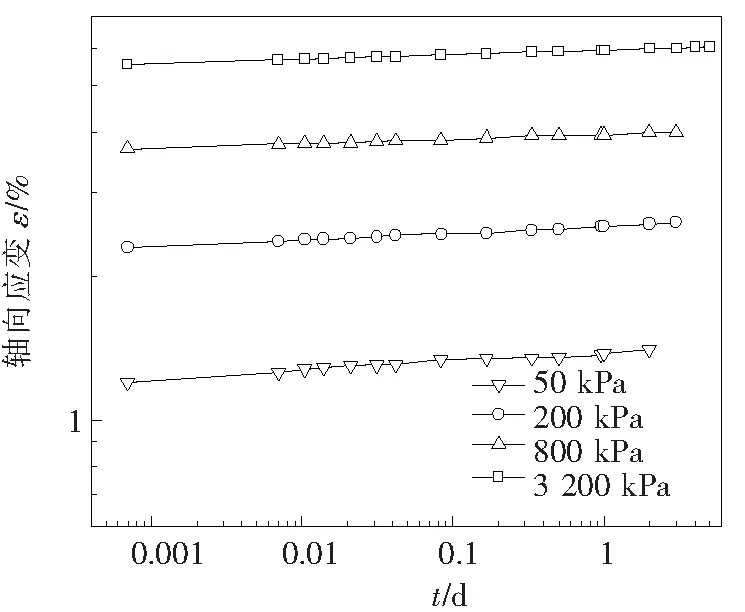
图3 双对数坐标下变形随时间的变化趋势
图4为自然坐标系下的应力应变等时曲线.从图中可以看出各时间下的等时曲线组成了一簇形状类似的折线.从中可以看出在低应力区间(50 kPa以内),各时间所对应的等时曲线非常靠近,几乎重合;但随着应力的增加(如增加到3 200 kPa),各时间下的等时曲线逐渐分开,这一现象也证明了饱和砂性土的变形同样具有滞后性.
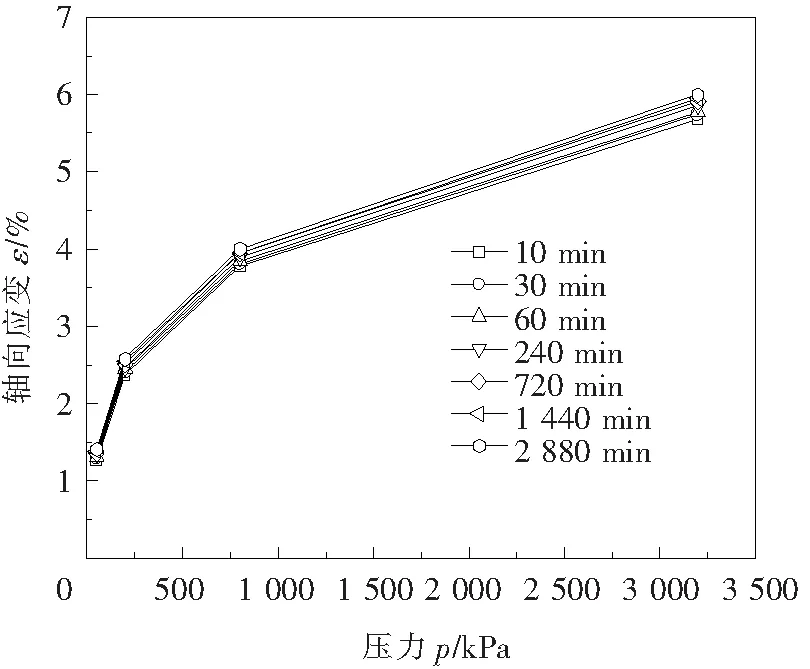
图4 应力应变等时曲线
3 流变模型
由试验现象和前面的分析可以看出,长三角地面沉降区饱和砂性土在高压应力下变形复杂,且同样具有蠕变特性.为了对该地区饱和砂性土的流变特性进行分析以及对地面沉降加以预测,需要在试验的基础上找出应力、应变和时间三者之间关系的数学表达式,即流变模型.所谓理论流变模型就是把砂土看作均质连续体,通过“虎克体”和“牛顿体”等基本元件的组合来模拟土体的复杂变形[14,23].
3.1 模型的选择
由试验可以看出该地区饱和砂性土在轴向应力的作用下,其变形为包括瞬时沉降、固结沉降和次固结沉降的衰减蠕变.因此在流变模型中必须要具有虎克弹簧来模拟土体在应力作用下所发生的瞬时沉降,且该虎克弹簧应与其他元件串联;其次为了模拟衰减蠕变的特征,流变模型中还应当具有牛顿黏壶.
不同模型所含有的元件种类虽然相同,但其所具有的元件个数和组合方式却是各异的,考虑到各地区土体物理力学性质的差异性,流变本构模型本身的反演问题(即如何根据实测资料辨识出最佳的流变模型)显得尤为重要.为此,本文找出了目前常用的5个能表征衰减蠕变的流变模型(Merchant体、开尔文体(K)、广义开尔文体(H-K)、Burgers体、饱依丁-汤姆逊体(H-M)),并将其蠕变公式和结构模型列于表2.
3.2 模型的识别
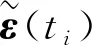
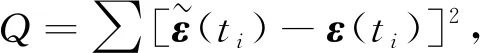
(1)
求得未知参数之后,在相同的时间向量下,由各模型的蠕变公式求出土体的蠕变变形理论值,并将其与试验测得的蠕变变形量绘制在同一个双对数坐标系中.其中理论值用实线代替,试验真实值用散点代替,如图5.
3.3 结果分析
根据数理统计,当相关系数R在0.4~0.6之间时两变量为中等程度相关,在0.6~0.8之间时为强相关,在0.8~1.0之间时为极强相关.由表3中的相关系数可知,5个模型的相关系数均大于0.5,即本文列出的5个流变模型对于该地区饱和砂性土变形的拟合在一定程度上都是可行的,也证明了饱和砂性土的流变性.
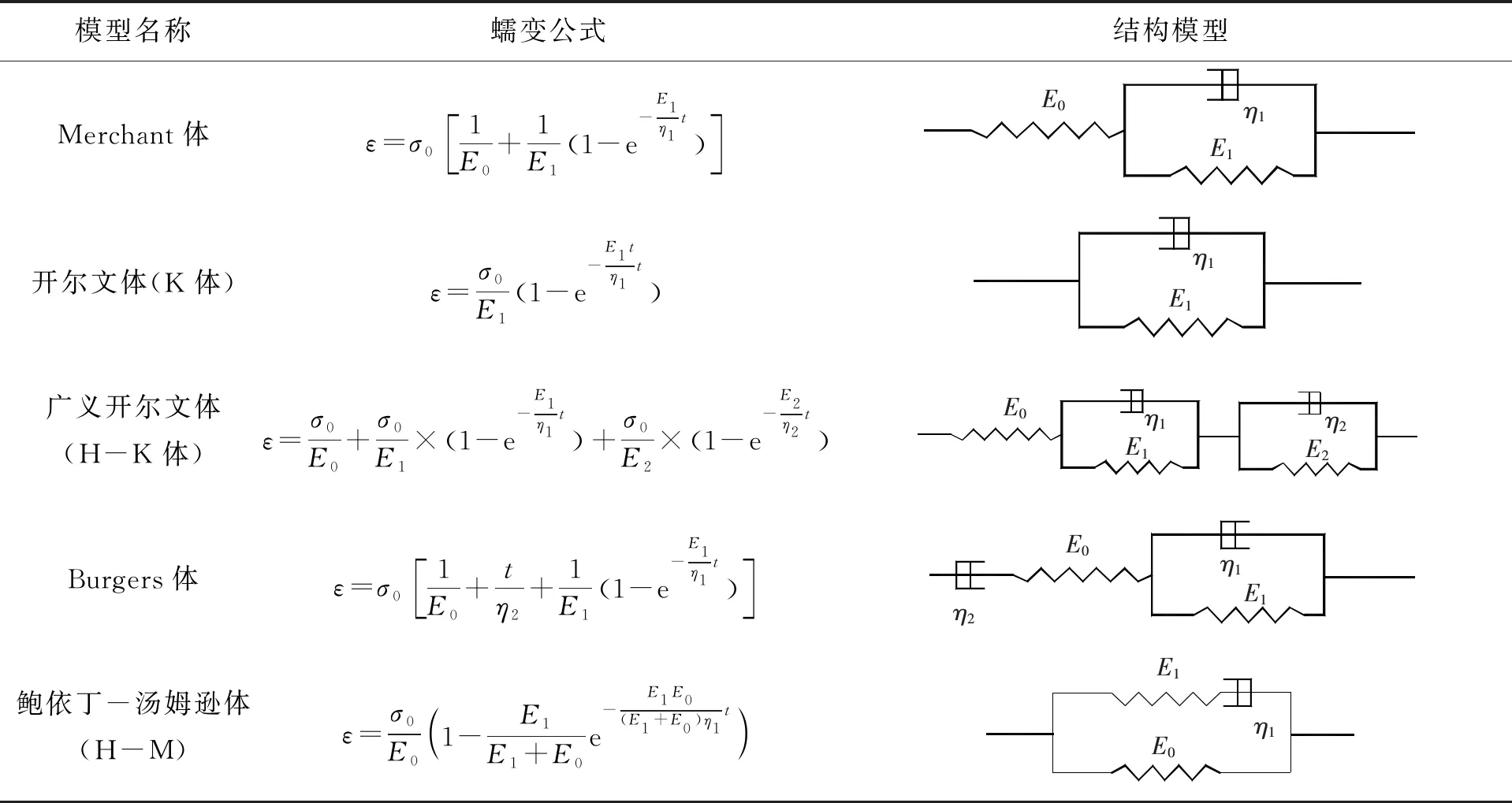
表2 常见流变模型的蠕变公式
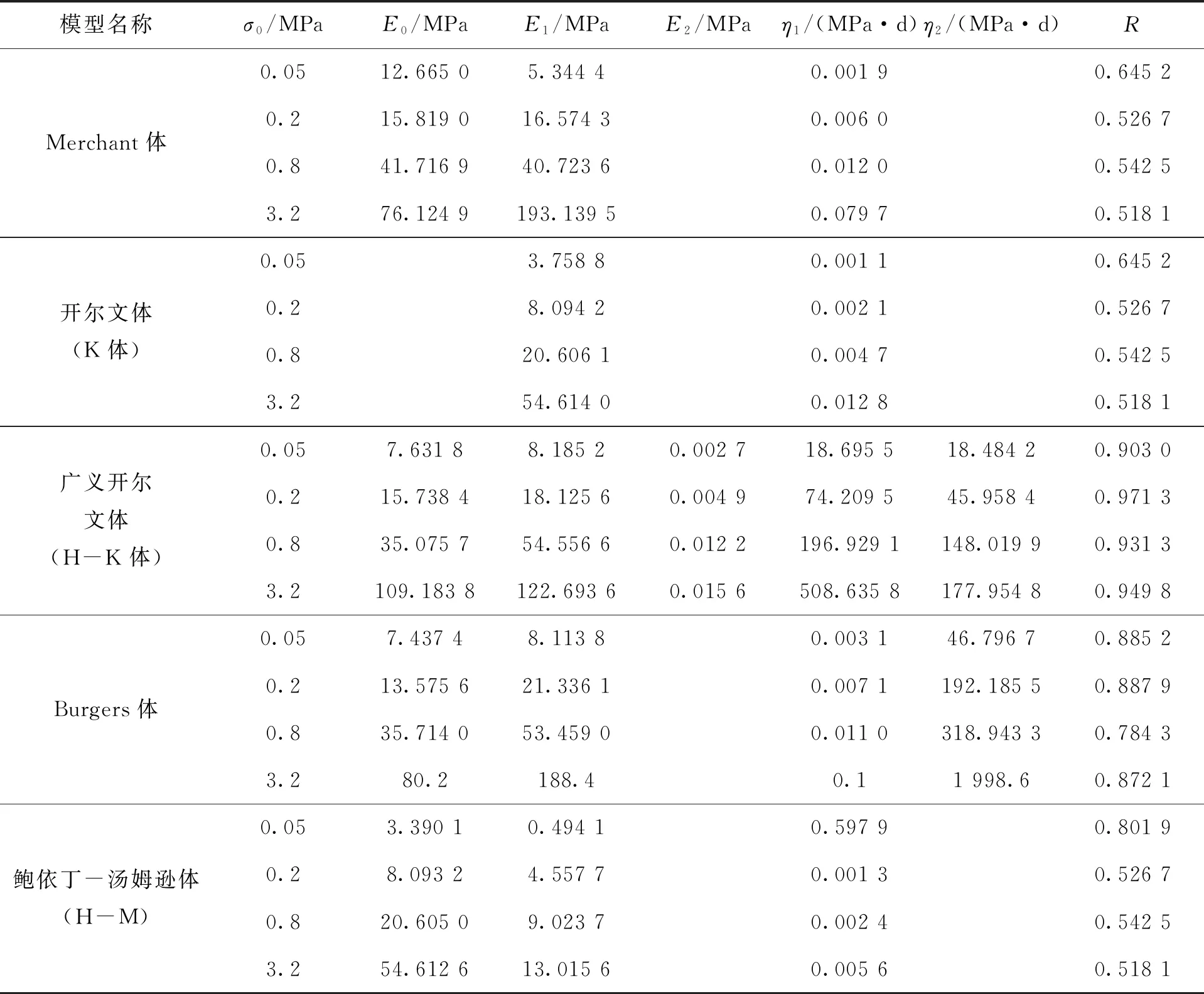
表3 参数反演结果
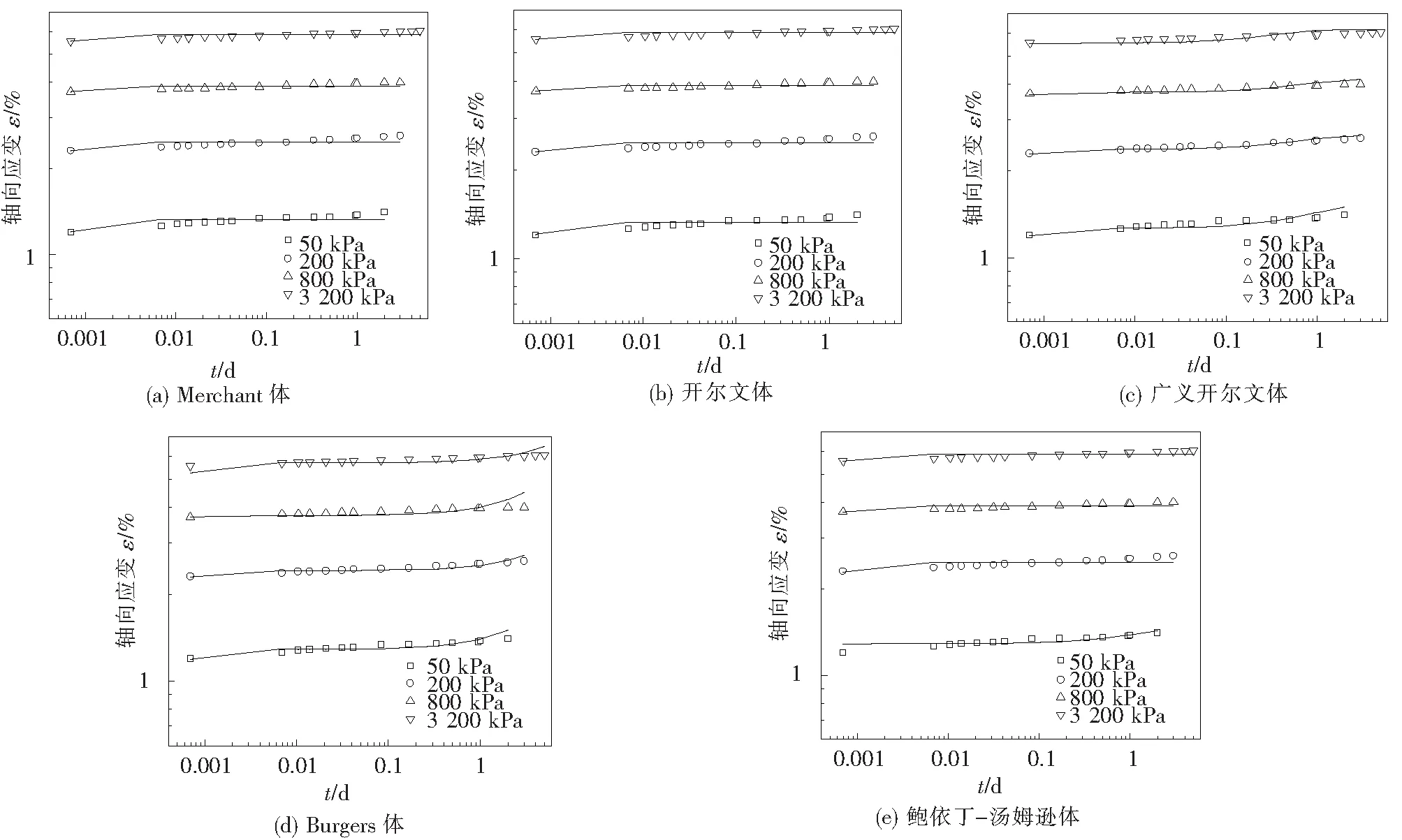
图5 模型计算结果与试验数据对比
对各流变模型在不同应力下的相关系数求平均值,结果见表4.可以看出广义开尔文体和Burgers体的平均相关系数均大于0.8,都属于极强相关,从表3各级应力下的相关系数也可以发现两者均能很好地对试验土样的蠕变特性进行拟合.其中广义开尔文体是五单元模型,Burgers体是四单元模型,相比较而言广义开尔文体参数更多,但其拟合精度更高,相关系数高出Burgers体9.5%.

表4 各模型的平均相关系数
从表3各模型参数的反演结果发现,同一模型的各参数和应力水平有关,随着应力的增加其反演结果也随之增加.如果假设模型一旦给定,其中参数值也应为定值.因为当应力增加时,为了保持模量不变,应变也应当增加相应的倍数.但是,土体是具有三相特性的典型非线性体,且当土体被压密挤实到一定程度之后,其孔隙比也将缩减到一定程度,同时伴随内部土体颗粒的滑移调整和颗粒破碎导致的级配改变.因此,为了更好地描述土体的这种非线性特点,可以采用一些非线性元件(如非线性弹簧)来组合模型,使得各参数(如弹簧的模量E)随应力的变化而不同[6].
4 结 论
(1)试验结果表明,瞬时加载下饱和砂性土的变形是具有明显阶段性的衰减蠕变,其应力应变等时曲线也显示饱和砂性土的变形同样具有流变性.在地面沉降计算分析中,应该同时考虑弱透水层黏性土和含水层砂土流变性带来的变形滞后效应.
(2)从常用的5个流变模型中识别出最佳模型.结果表明,广义开尔文体和Burgers体都能对长三角地面沉降区饱和砂性土的蠕变趋势加以描述.其中广义开尔文体的平均拟合相关系数高出Burgers体9.5%,精度更高,是描述该地区饱和砂性土流变特性的最优模型;但Burgers体所含参数少于广义开尔文体,相比较而言应用更方便.
(3) 由于所选的流变模型由线性元件组合而成,本文中同一模型在不同应力下所反演出的参数不同,不能用某一级应力下反演出的参数来描述其他荷载下的流变规律.为了更好地模拟土体这种非线性材料,有必要对模型进行改进,采用非线性元件,使得模型参数随着应力变化而改变,这方面仍有待开展进一步的理论和试验研究.
——以开尔文公式为例

