高精度四轴自动搬运机器人实验平台的设计与分析

陈修龙， 李劲文， 盛永超

（山东科技大学机械电子工程学院，山东青岛266590）

0 引 言

目前，工业机器人广泛应用于工业生产制造及物流等行业中，尤其是搬运机器人以其智能化、高效率及和谐的人机交互［1］等特点，在自动化搬运作业中受到了极大的欢迎，能极大地提高劳动生产效率，使企业在市场竞争中具有更大的优势和竞争潜力。

美国AMF公司研发出一款名叫Versatran的应用于工业生产的机器人，其机械手结构在工作过程中可以完成腰部的圆周整转动作，在竖直方位上的升降动作，以及工作空间范围内的伸缩运动［2］。日本安川公司研发的名为MPL160的堆叠机器人末端执行器的负载能力高达160 kg［3］，其末端重复定位精确度可达到±0.5 mm。德国KUKA公司对机器人的开环式结构框架脱离了有线控制，使机器人操作更加方便、更加智能化，并将三维空间物体辨别系统应用到了机器人视觉领域［4-5］。而在国内工业机器人的研究中，王琪等［6］利用Adams对搬运机器人的杆长进行参数化设计，从而实现搬运机器人机构的优化设计。杨国军等［7］提出了一种以模糊原理为基础的遗传算法，并基于此遗传算法提出了机械手末端轨迹规划的时间最优设计方案。白晶等［8］设计了能够应用于4自由度码垛搬运机器人的模糊PID控制算法，有效地改善了多轴机器人控制器的控制精度。王占军等［9］利用Ansys中模态分析板块，对码垛机器人的三维模型进行模态和振型分析，找出机器人在工作时的脆弱环节，为优化构型提供理论基础。

本文设计了一种有效载荷15 kg的四轴4自由度自动搬运机器人平台，能够高速、高精度地完成任务。首先对整体机构进行结构设计，通过利用Solidworks对机器人进行三维建模，然后将三维模型导入Adams中进行运动仿真，得到各驱动杆件和末端旋转台的工作转矩和运动学特性，根据工作转矩对电机类型进行选择。运用Ansys有限元仿真对机器人关键杆件和脆弱部位进行刚度和强度校核，保证整个机构在额定工作状态下运行的可靠性和稳定性。

1 机器人平台3D模型的建立

高精度四轴自动搬运机器人由底座、旋转台、末端执行器和3个主杆以及3个连接杆组成。初定搬运机器人的主要技术参数如下：搬运次数12次／min，最大行程1 800 mm，本体质量160 kg，有效载荷15 kg，底座限位范围±360°，J1 限位范围＋105°，－50°，J2 限位范围＋105°，－25°，J3 限位范围±168°，定位精度1 mm。由此可确定各运动杆件及连杆的旋转中心距：主杆1为625 mm，主杆2为620 mm，连杆1为610 mm，连杆2为260 mm。

设计建立的机构三维模型如图1所示。

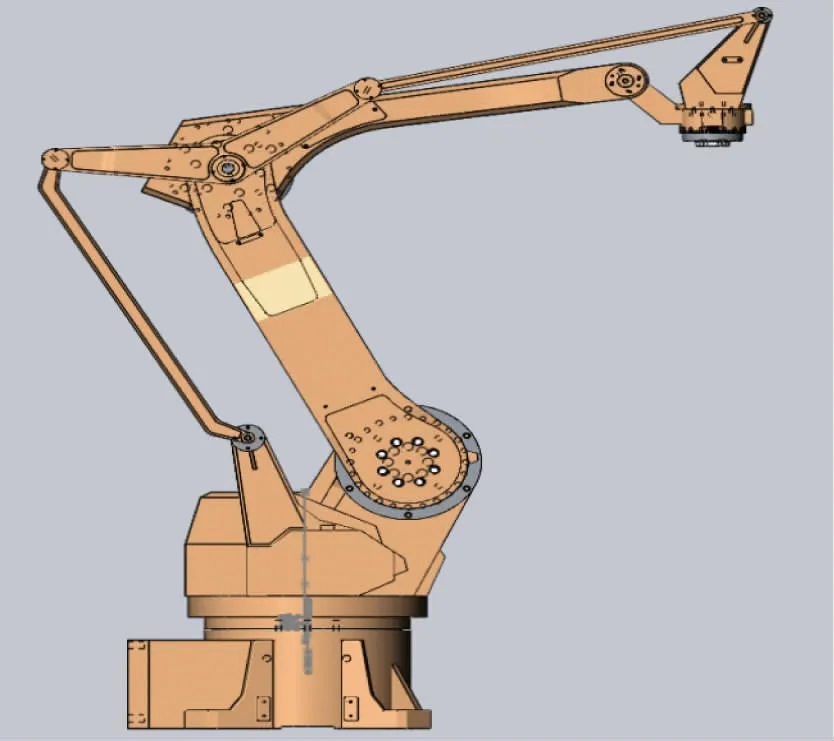
图1 高精度四轴自动搬运机器人三维模型

2 机器人平台驱动装置选型

电动机作为一个运动机构中非常重要的组成部分，它的选型要综合考虑各方面的要求，以此来保证机构能够发挥出电动机的所有工作性能［10］。电动机的选型原则主要包含下列几个方面：①机构运行时，其连续工作转矩需小于电动机的额定扭矩；②瞬时最大转矩要小于电动机的最大扭矩；③运动件的连续工作速度小于电动机的额定转速；④负载惯量要与转子惯量在数值上相匹配［11］。

将机构模型导入Adams中进行正解仿真分析，给定一个门型工作轨迹，通过仿真，得到4个驱动转动副的转矩变化如图2～4所示。

图2 旋转台转矩变化图

图3 主杆1转矩变化图

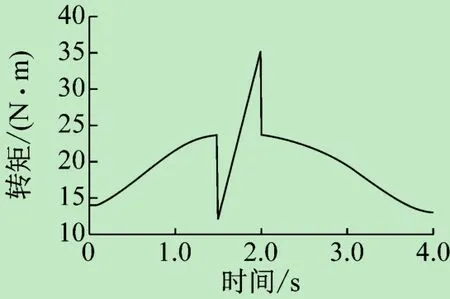
图4 主杆2转矩变化图

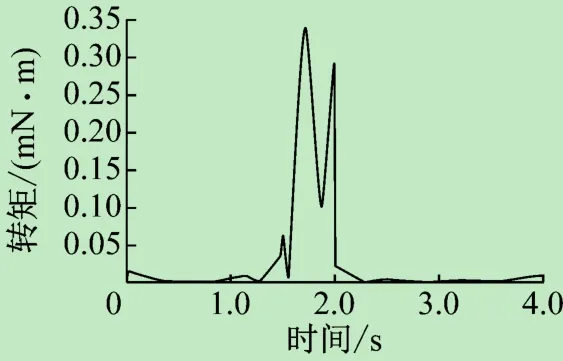
图5 末端转矩变化图

由机构工况可知，旋转台及主杆是在一个很短的时间达到一个速度峰值，而后为了使其停止，就需要通过扭矩控制给予其一个方向转矩。由上面转矩变化图可知，旋转台所需最大驱动转矩为313 N·m，主杆1所需最大驱动转矩95 N·m，主杆2最大驱动转矩36 N·m，末端最大转矩0.34 N·m，所以旋转台、主杆1和2、末端执行器的驱动转矩要分别大于313、95、36、0.34 N·m。底座选用IS型蜗轮蜗杆减速器，减速比为17，主杆和末端都选用谐波减速器，减速比分别100、80、100，则

式中：Mq为电动机转矩；Md为杆件最大驱动转矩；i为减速器减速比；η为该转动副处电机输入至杆件输出的效率（旋转台处效率为75%，其余各处均为80%）。

根据式（1）可得到旋转台处电动机需要的额定转矩不小于24.55 N·m，主杆1的驱动电动机的额定转矩不小于1.25 N·m，主杆2处电动机的额定转矩不小于0.56 N·m，末端执行器处的电动机转矩须大于4.25 μN·m。对于电动机的功率，有

式中：P为电动机功率；F为工作压力；v为工作行程速度。根据式（2）和各杆件最大转速可分别得到旋转台、杆件、末端处电动机的大致功率：4，1，0.6，0.05 kW。由此选得电动机如表1所示。

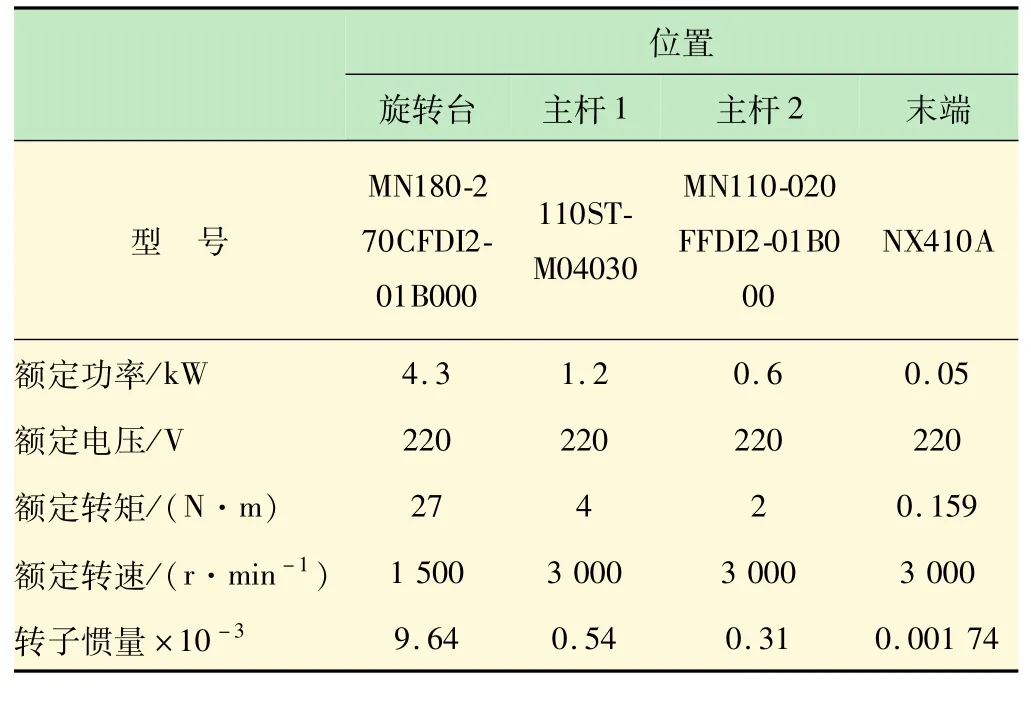
表1 四轴驱动机器人所选取的电机及其参数

3 机器人平台运动学仿真

Adams软件是一种在机构运动学和动力学分析广泛应用的软件，能够集建模、求解、可视化技术为一体［12］，进行机构的动力学及运动学仿真分析时，能清晰地了解到机械系统的运动性能［13］。

通过Adams仿真得到3个主要运动件的角位移、角速度、角加速度图，如图6～8所示。

图6 旋转台、主杆1、主杆2角位移

由图可知，旋转台的角位移变化范围在0～－90°，角速度变化范围是0 ～270°／s，角加速度变化范围为0～2 100°／s2；主杆1的角位移变化范围在0～60°，角速度变化范围在0～60°／s，角加速度变化范围在0～158°／s2；主杆2的角位移变化范围是－5～15°，角速度变化范围在0～15°／s，角加速度的变化范围是0～40°／s2。速度、位移曲线走势平缓，在给定运行轨迹时，不会发生震动，有较好的运动性能。

图7 旋转台、主杆1、主杆2角速度

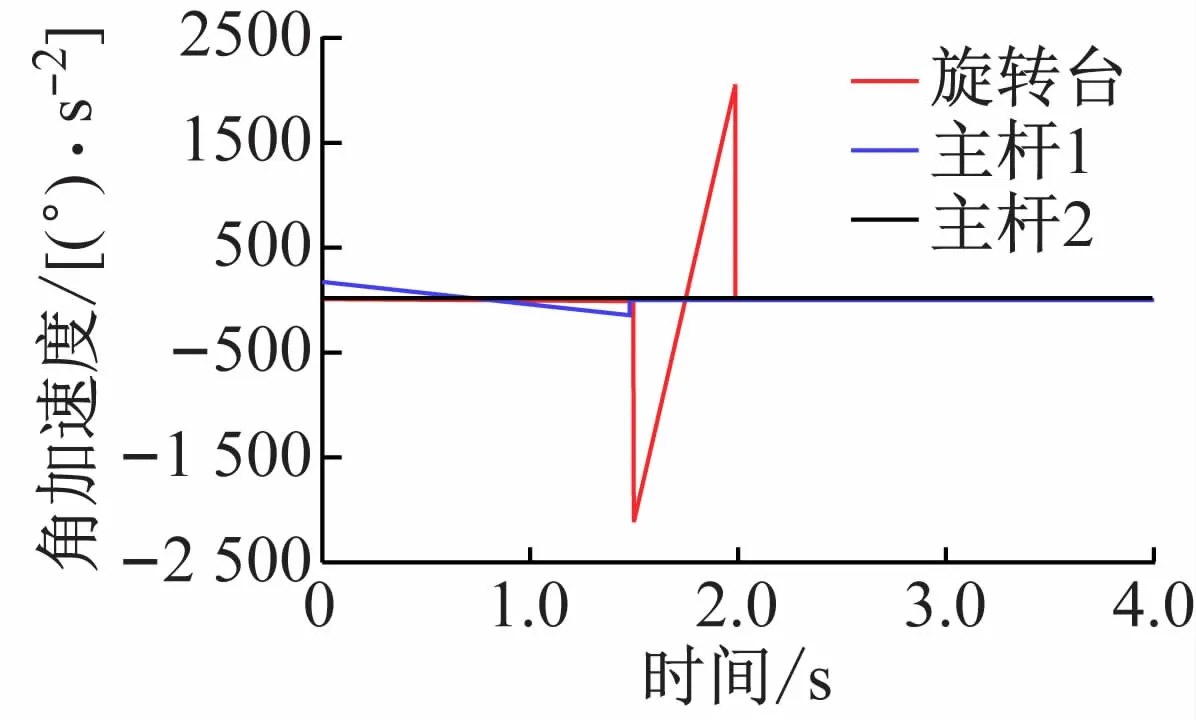
图8 旋转台、主杆1、主杆2角加速度

4 机器人平台有限元仿真及模态分析

在整个机构的运行过程中，为确保末端执行器能够精准地完成工作任务，各运动件的刚度和稳定性十分重要，其中主杆1、2，底座等关键部位的结构强度更是重中之重。通过仿真其极限工况，得到其应力变形图，分析最大应力及变形程度。判断是否超出所选材料的许用应力范围，检验机构模型的合理性［14］。

底座主要受力位置在上端面放置轴承处，主杆1处的转矩和受力来源于减速器传递的转矩，通过仿真对此部位进行应力与变形分析。底座与主杆材料均选用铝铜合金ZL201，屈服强度最小值为330 MPa，取安全系数为3，则其许用应力为110 MPa。根据转矩及受力图，给定底座一个1.5 kN的压力；在主杆1上端轴孔处添加525 N的轴承载荷，通过仿真得到变形与应力分布图，如图9～12所示。

图9 底座变形分布图

图10 底座应力分布图

图11 主杆1变形分布图

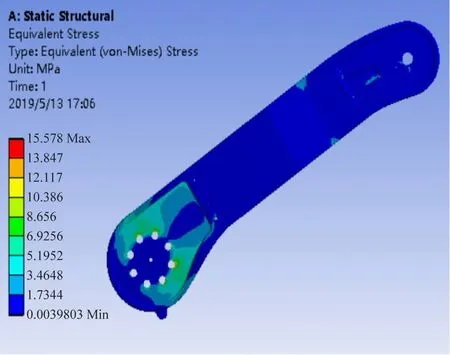
图12 主杆2应力分布图

由图可知，底座最大变形量仅0.003 5 mm，主杆1的变形量最大为0.162 2 mm，结构合理；底座最大应力为0.541 MPa，主杆1 最大应力为15.578 MPa，远小于许用应力，满足强度条件。

机器人结构的动态特性对其精度和可靠性也会产生很大的影响［15］，搬运机器人在工作过程中需要实现前进后退等动作，并在夹取货物过程中会有升降、旋转等动作，因此其在工作过程会出现晃动振动的现象，所以有必要深入了解其动态特性，这可以为其结构的合理设计与改进提供理论依据。对受力最大的杆1进行模态分析，将模型导入Ansys中，求解得其各阶频率及模态对应的振型图，如图13～19所示。

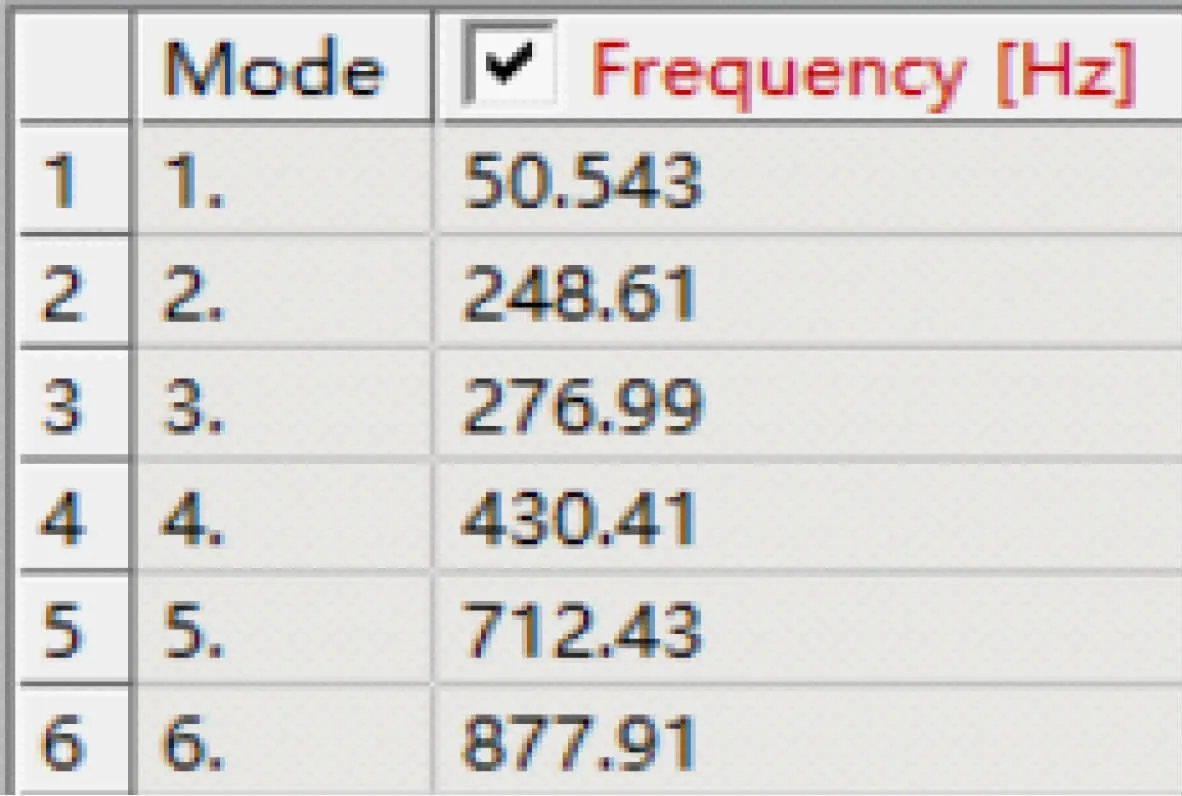
图13 主杆1前6阶固有频率

图14 主杆1一阶模态振型

图15 主杆1二阶模态振型

图16 主杆1三阶模态振型

图17 主杆1四阶模态振型

图18 主杆1五阶模态振型

图19 主杆1六阶模振型

从图可以看出，前3阶主要是主杆1上端在XZ平面的振动，即上端在XZ平面出现偏移，将会影响末端执行器前进后退的运行精度，因此需要着重考虑主杆1上端在XZ平面的共振问题。后3阶中，主杆1在Z轴方向上出现了明显的扭转现象，对整个机构的稳定性产生重大影响，若在此模态发生共振将会使整个装置上部稳定性变差。由上可知，主杆1上部是主要的动态特性影响因素，需要适当增加厚度或提高材料刚度来改进。

5 结 语

本文设计了一种高精度四轴自动搬运机器人平台，首先对机构整体的结构和尺寸参数进行设计；再利用Adams进行机构的动力学与运动学仿真，得到装置构件在运行过程中的位移、速度、加速度和力以及转矩曲线图，由受力和转矩对机构所需的驱动装置进行选择；用Ansys对关键零部件进行应力、变形及模态分析，校核其刚度和强度，保证整个装置在运行过程中的安全性和可靠性。