全开缝式翅片管换热器结构参数优化
王 方, 王鹏超, 徐 强, 梁静静, 王 恒
(中原工学院能源与环境学院,郑州450007)
0 引 言
随着我国节能减排目标的提出与实施[1],节能问题深受各行各业的关注,在建筑能耗问题方面,空调行业占据了重要的一部分,其中,换热器的换热性能是空调系统节能与否的主要因素之一。目前,对于空调系统末端设备最常用的换热器是翅片式换热器,其主要类型有平直形、条缝形、波纹形、百叶窗形等,由于传热效率较低,易积灰尘,阻力较大等不足[2],发展出了多种新型翅片,旨在通过结构形式的改变来提高翅片式换热器的综合换热性能。Lozza等[3]通过Luve Contardo试验台对15根相同管径、相同尺寸,但不同形状的翅片式换热器进行换热性能测试,发现不同形状翅片的换热器,其换热性能相差较大。王厚华等[4]采用数值模拟的方法将三对称大直径圆孔翅片与矩形翅片进行对比,得出其表面传热系数比平翅片高25%。Duan等[5]对波纹翅片平板管换热器翅片侧的流动和传热特性进行了数值研究,得到了努塞尔数与摩擦系数的关系;Halici等[6]通过实验研究了平直翅片管式换热器关于管排数对其换热性能及流动特性的影响;Liu等[7]提出了对翅片式扁管换热器的优化方案,进行了传热系数和压力损失的数值计算,并分析了物理性能对换热的影响。Pis’mennyi等[8]提出了一种新型的非完全翅片扁圆管形式的扩展传热面,并与传统的翅片圆管换热器进行对比,得出其换热效果相对较好;费继友等[9]通过数值模拟计算的方法对平直翅片式换热器结构形式进行优化,进而提高换热器的换热效率;Chu等[10]通过数值模拟和实验验证的方法,对比分析了不同翅片间距、管间距及管径对圆管和椭圆管形式的波纹翅片管换热器的影响;赵亚萍等[11]通过采用三维数值模拟的方法,对顺排、错排和错列3种不同排列方式的矩形翅片椭圆管换热器进行性能分析;章国芳等[12]研究了在顺排、叉排两种排列方式下的翅片管换热器管外流场速度、摩擦系数等分布特性;何明勋等[13]研究了翅片管换热器内部流场及温度场的分布情况,并通过实验进行验证。
本文针对全开缝式翅片管换热器,通过因素分析法对翅片管的横纵向间距、翅片厚度、翅片长度、翅片宽度和翅片间距等结构参数优化设计,得出最优结构参数,使其综合换热性能达到最佳效果,在满足环境舒适度的同时,达到节能减排的目的。
1 模型建立
Zhao等[14]研究的矩形翅片椭圆管换热器模型和杨文静等[15]研究的圆形翅片换热器物理模型均已被验证与实际问题相符,本文所研究的全开缝式翅片管换热器模型是在两者的基础上建立的,因此可间接地验证为准确可靠的。
1.1 几何模型
本文主要是在平直翅片管换热器与开缝翅片管换热器的基础上提出的一种新型的全开缝换热器,圆管从每个翅片中心穿过,管道为四管程错排形式,材质为铜管,翅片的材质为铝片,管内流动液态低温冷水,外侧由高温空气略过翅片。由于翅片周期性的排列在管外,取相邻两排翅片之间的区域为研究对象,通过数值模拟的方法,对翅片管的横纵向间距、翅片厚度、翅片长度、翅片宽度和翅片间距等结构参数进行优化。该模型的基本结构图如图1所示。

图1 全开缝式翅片管换热器基本结构图
1.2 数值模型
(1)基本假设。翅片管换热器的换热过程主要针对如下假设:①流体为不可压缩流体;②换热及流动过程为稳态传热过程;③铜管与铝翅片之间不考虑接触热阻;④流体水平吹过翅片,且入口处温度一致;⑤流体、铜管、铝翅片物性参数均为定值。
(2)网格划分。根据翅片排列的对称性及周期性,选取相邻两翅片中心面之间的区域为计算域,用ICEM CFD软件进行模型建立,对固体流域与流体流域进行划分,并采用结构化网格的划分方式进行网格划分,最大网格尺寸不超过1.5 mm,整体网格质量Determinant 3×3×3保持在0.75以上,计算域生成的网格示意图如图2所示。

图2 计算区域网格示意图
(3)边界条件。选定计算域的左端面为速度进口,设定速度为2 m/s,温度为298 K,右端面为压力出口;前后面均设定为对称面,上下面为绝热面;铜管壁面温度设定为290 K,且翅片与铜管接触面温度与铜管温度一致;与流体接触的翅片表面传热方式为流固耦合传热方式。
1.3 正交试验设计
本文主要是从翅片管的横纵向间距、翅片厚度、长度、宽度和间距6种因素对换热器换热系数进行分析,同时还要考虑到换热系数、换热面积及换热温差等对换热量的综合影响,每种因素选取5种尺寸,其结构尺寸见表1。
为了快速、高效地得到多因素多水平形式中的最优结果,同时对单个因素独立分析,与其他因素不发生互交作用,可采用正交试验设计的方法,利用正交性从试验中选取出具有代表性的组合。本文是一个6因素5水平的问题,选用正交表L25(56)进行试验设计,其正交试验因素分析如表2所示。

表1 换热器结构尺寸 mm

表2 正交试验因素水平 mm
2 计算结果及分析
利用Fluent软件对正交实验设计得出的25种方案进行数值计算,计算模型选取Laminar模型,求解计算方法采用Coupled算法,其中,梯度项差分采用Least Squares Cell Based格式,压力项差分采用Second Order格式,动量项和能量项采用Second Order Upwind格式,各项松弛因子采用默认设置。经数值计算得出如表3所示的试验结果。
正交试验的25次试验结果中,将各因素各水平的试验值累加后求平均值,其结果如表4所示。表4中R为同一因素不同水平之间ki的最大值与最小值之间的差值,即为极差。在同一种因素中,R越大,反映了水平变化对试验结果的影响越大;相反,其水平变化对试验结果影响越小。

表3 正交试验数值计算结果
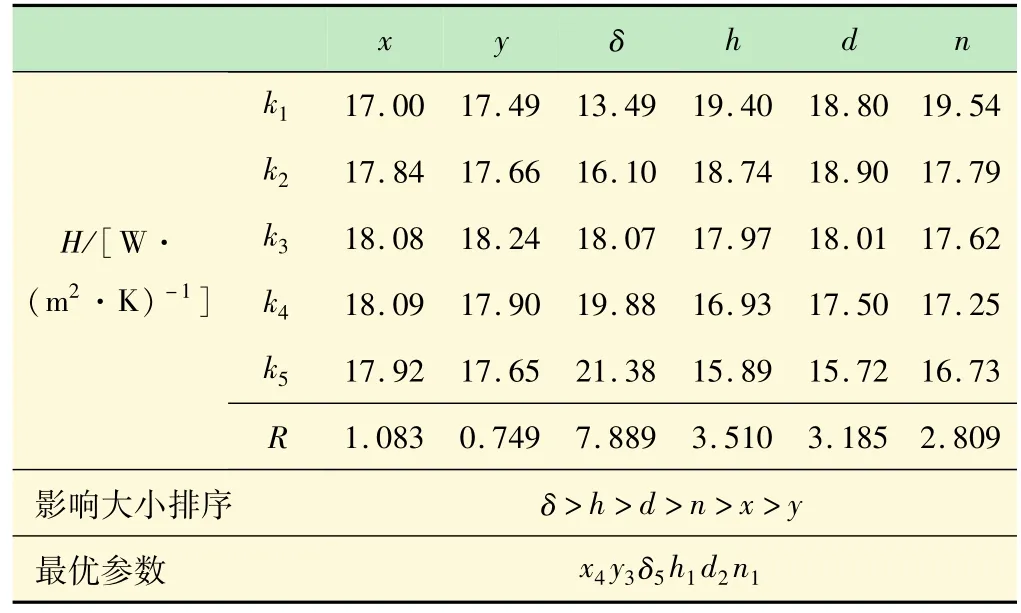
表4 正交试验直观分析 mm
表中,R值反映6种因素对换热系数的影响程度从大到小的顺序为:δ>h>d>n>x>y;由于换热系数越大换热效果越好,因此对于换热器的结构参数的最优组合为:x4y3δ5h1d2n1,其具体优化结构参数如下:x=135 mm,y=22 mm,δ=0.6 mm,h=90 mm,d=65 mm,n=2 mm。
为了便于分析换热系数变化情况,分别作出各因素不同水平对换热系数的影响趋势图。由图3可见,翅片厚度对换热系数的影响最大,翅片长度、宽度、间距对换热系数的影响间距次之,横向间距和纵向间距的影响最小。
对于翅片管换热器的x、y,其值变化主要是用来增加流体的扰动,进而减小流体边界层厚度,以达到增强换热的目的。从图3(a)、(b)可知,对于x和y在选取的区域范围内,对换热系数的影响是先增大后减小,并不是其值越大,换热系数就越大,因此,可以得出,x=135 mm、y=22 mm时在选取的范围之内为最佳效果。
h和d主要是用来决定换热接触面积的大小,进而影响整体换热的效果。由图3(d)、(e)可见,换热系数随着翅片长度的增大而减小,随着翅片宽度的增大先增大后减小。这说明,换热面积过大不仅不能促进换热,反而会使换热系数降低;若继续减小翅片长度,则会导致开缝过大,致使换热面积过小而影响换热。因此,在选取的区域范围内,h=90 mm、d=65 mm时换热效果更好。
如图3(c)、(f)所示,从理论上分析可知,换热系数随翅片厚度δ的增加而增加,但是其变化趋势变缓。这说明,换热系数受δ影响的变化率在缩小,若继续增大δ,则会使翅片管换热器的经济性下降;换热系数随翅片间距n的增大呈下降趋势,且n=2 mm时的换热系数明显高于其他值,这是由于翅片间距过小,致使两翅片间的边界层相互干扰,对换热系数影响最大。若继续减小翅片间距,不仅会使进出口压降增大而浪费能源,还会使生产成本提高。因此,经综合考虑,δ=0.6 mm、n=2 mm时换热状态符合实际应用。

图3 各因素对换热系数的影响趋势
3 最优参数模拟分析
根据以上的正交试验直观分析得出全开缝式翅片换热器的最优结构参数,对其最优结构参数的翅片换热器进行数值模拟计算,得出其最优换热系数如下:x=135 mm,y=22 mm,δ=0.6 mm,h=90 mm,d=65 mm,n=2 mm,H =28.73 W/(m2·K)。
为了便于形象地显示出计算域的整体分布情况,通常使用云图来表示。本文主要选用速度云图及温度云图对空气域的中心面处及翅片表面处进行分析。图4、5分别为中心面处和翅片表面处的温度云图。随着换热的进行,空气温度随流动方向逐渐降低,前两排翅片处的空气温度梯度变化明显高于后两排,最前面的翅片表面处的温度梯度变化相对较大,在圆管的背面有一不发生换热或换热现象较弱的区域,主要是由于空气的滞留和翅片表面流体边界层所致;图6、7为中心面处和翅片表面处的速度云图,可以看出,在管壁背风面存在滞留区,在此区域,换热现象不明显,中心面处的速度梯度变化比翅片表面处均匀,且中心面速度相对较高,翅片表面处的速度大小相对较低,在空气流通截面较窄处,气流速度最高可达到5 m/s。
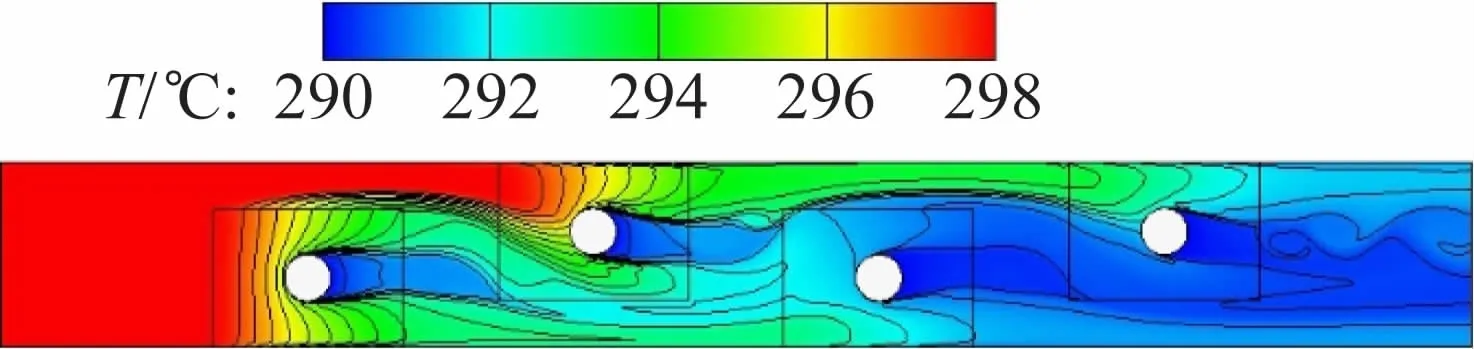
图4 中心面处温度云图

图5 翅片表面处温度云图
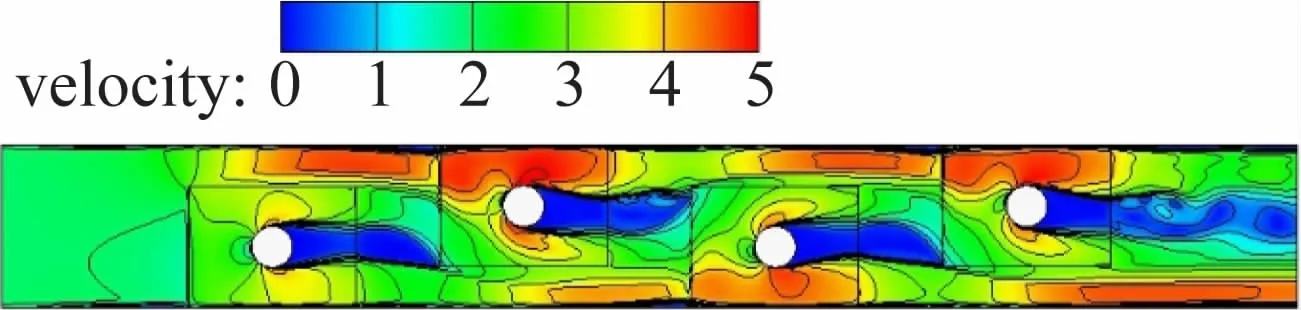
图6 中心面处速度云图

图7 翅片表面处速度云图
4 结 语
(1)通过正交试验的方法对翅片管换热器的横纵向间距、翅片厚度、翅片长度、翅片宽度和翅片间距主要因素进行设计,并进行数值模拟分析。得出,最优结构参数为横向间距135 mm,纵向间距22 mm,翅片厚度0.6 mm,翅片长度90 mm,翅片宽度65 mm,翅片厚度2 mm。
(2)通过对最优结构参数的翅片管换热器进行模拟计算,得出在合理选取的参数范围之内其最大平均表面换热系数为28.730 W/(m2·K)。
(3)利用云图对计算域整体分析,可知空气温度随流动方向逐渐降低,前两排翅片的换热效果比后两排明显;管壁的被风面存在滞留区,导致此处的换热现象不明显;在空气流通截面最窄处,最高气流速度可达5 m /s。
·名人名言·
大学的荣誉,不在它的校舍与人数;而在于它一代一代人的质量。
——柯南特

