基于Blackman 窗六谱线插值FFT 谐波分析方法
汪旭明, 田 堃, 雷可君, 王向明, 杨 喜
(1.吉首大学a.物理与机电工程学院;b.信息科学与工程学院,湖南吉首416000;2.上交所技术有限责任公司,上海200120)
0 引 言
电网中大量非线性元件的存在导致谐波和间谐波的产生,并严重威胁到电网本身的安全运行。因此,谐波参数的准确估计对于电力系统的监控和保护有着重要的作用[1-3]。然而,由于非同步采样及非整周期截断等因素的影响[4],如何准确地估计谐波的频率、幅值及相位等信息引起了研究者的广泛关注。
现有的谐波分析方法有快速傅里叶变换(FFT)法[5-9]、神经网络法[10-11]、小波变换法[12-13]、瞬时无功功率法[14]等。其中FFT方法由于工程实现的简单而被广泛研究,但是由于基波频率处于波动状态使得采样处于非同步状态,在进行FFT处理时将不可避免地引起频谱泄露问题,从而导致谐波参数估计精度非常低。为此,许多学者提出了通过加窗插值的方法来减小频谱泄露的负面影响,进而提高谐波参数估计的精度。主流的处理方法包括:采用加Hanning窗、Hamming窗、Blackman窗等与单谱线、双谱线插值相结合的方法等[5-8]。这些方法虽然一定程度上可以提高信号参数的估计精度,但其估计效果仍有待进一步提高。
本文利用主次谱线及其相邻近谱线的信息,提出了一种基于Blackman窗的六谱线插值算法,并给出了谐波参数估计的修正公式。仿真实验表明,该算法能有效地提高了信号参数估计的精度。
1 Blackman窗的特性
对信号加窗后进行FFT处理可以有效地抑制非同步采样带来的频谱泄露,但是不同的窗函数对频谱泄露的抑制效果并不相同,由于余弦窗具有良好的旁瓣特性和简单的表达形式,故在实际的谐波分析处理过程中一般选择余弦窗。余弦窗的时域表达式为

式中:M表示窗函数的项数;N表示窗函数的长度,n=1,2,…,N -1,系数满足经典的3种窗都属于余弦窗,其系数取值见表1。
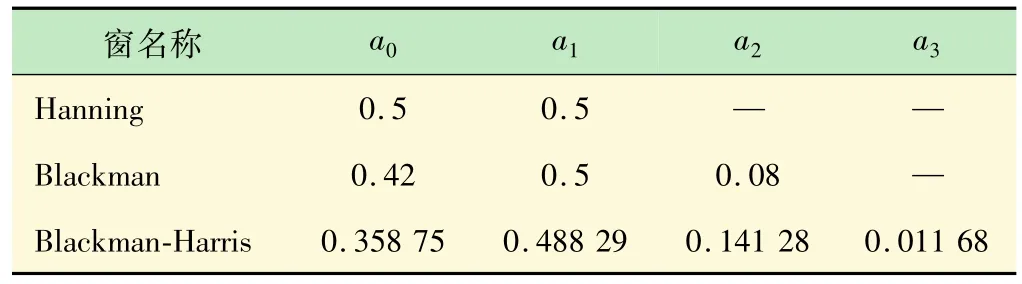
表1 3种典型余弦窗的系数
本文比较了上述3种典型余弦窗函数的旁瓣峰值电平和旁瓣衰减情况,其对数频谱图如图1所示。3种典型余弦窗的谱特征参数如表2所示。
图1和表1的结果表明,尽管在上述3种窗中Hanning窗实现最为简单,且具有最小的主瓣宽度,但其旁瓣峰值很大,不利于抑制频谱泄露;而尽管Blackman-Harris窗具有最小的旁瓣峰值,但其主瓣较宽,同时实现复杂度也较高。相比较而言,Blackman窗具有较小的旁瓣峰值以及主瓣宽度,且其实现复杂度适中便于实时计算,因而本文采用Balckman窗作为谐波分析过程中采用的窗函数。由表1可知Blackman窗的时域表达式为:
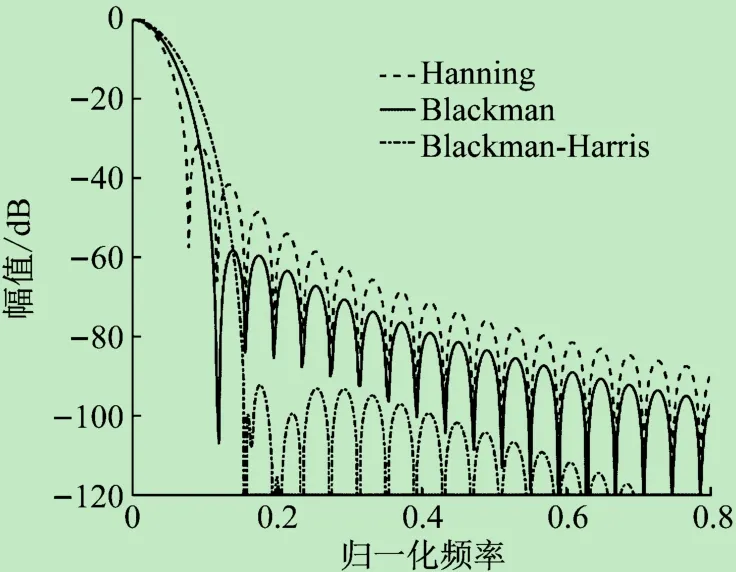
图1 3种余弦窗函数的对数频谱图

表2 3种典型余弦窗的旁瓣特性

相应地,不难得到其频谱函数为:

2 基于Blackman窗的六谱线插值算法
为简化分析过程,这里仅以单频信号为例进行分析,所得结果可以直接推广到多频复合信号的分析应用场景[15]。假定单频率信号表达式为

式中:A0、f0、θ0分别表示信号的幅值、频率和相位参数。对x(t)离散化可得:
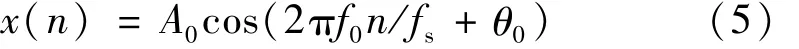
式中:fs为采样频率,n=0,1,…,N -1,N 为采样点数。对式(5)加窗后进行离散时间傅里叶变换得到:

式中:ω0=2πf0/fs;W(ω)为窗函数的连续频谱函数。由于复谱序列具有对称性,在参数分析过程中通常忽略负频点的影响,此时有:
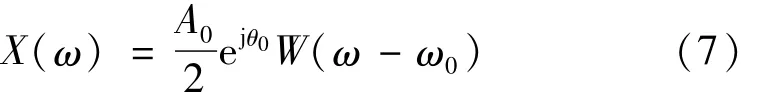

由于谐波信号的基波频率处于波动状态,故采样时很难做到同步采样。当对谐波非同步采样时,会造成频谱泄露从而使得真实峰值很难处于离散的频点上,此时k0可以用一个非整数来表示。设k=k0-δ-0.5,这里δ∈(-0.5,0.5)。假设kd和kd+1为真实峰值谱线附近幅值最大的两根谱线,其中kd<k<kd+1,kd+1= kd+1。取这两根谱线邻近的4 条谱线kd-2、kd-1、kd+2和kd+3。因为kd和kd+1最靠近真实峰值频率,对参数估计的影响最大,所以在频谱参数分析过程中对这两根谱线赋予最大的权值6,而对第kd-2、kd-1、kd+2、kd+3根谱线赋予的权值分别为1、2、2、1[15]。由式(3)得到[16]:

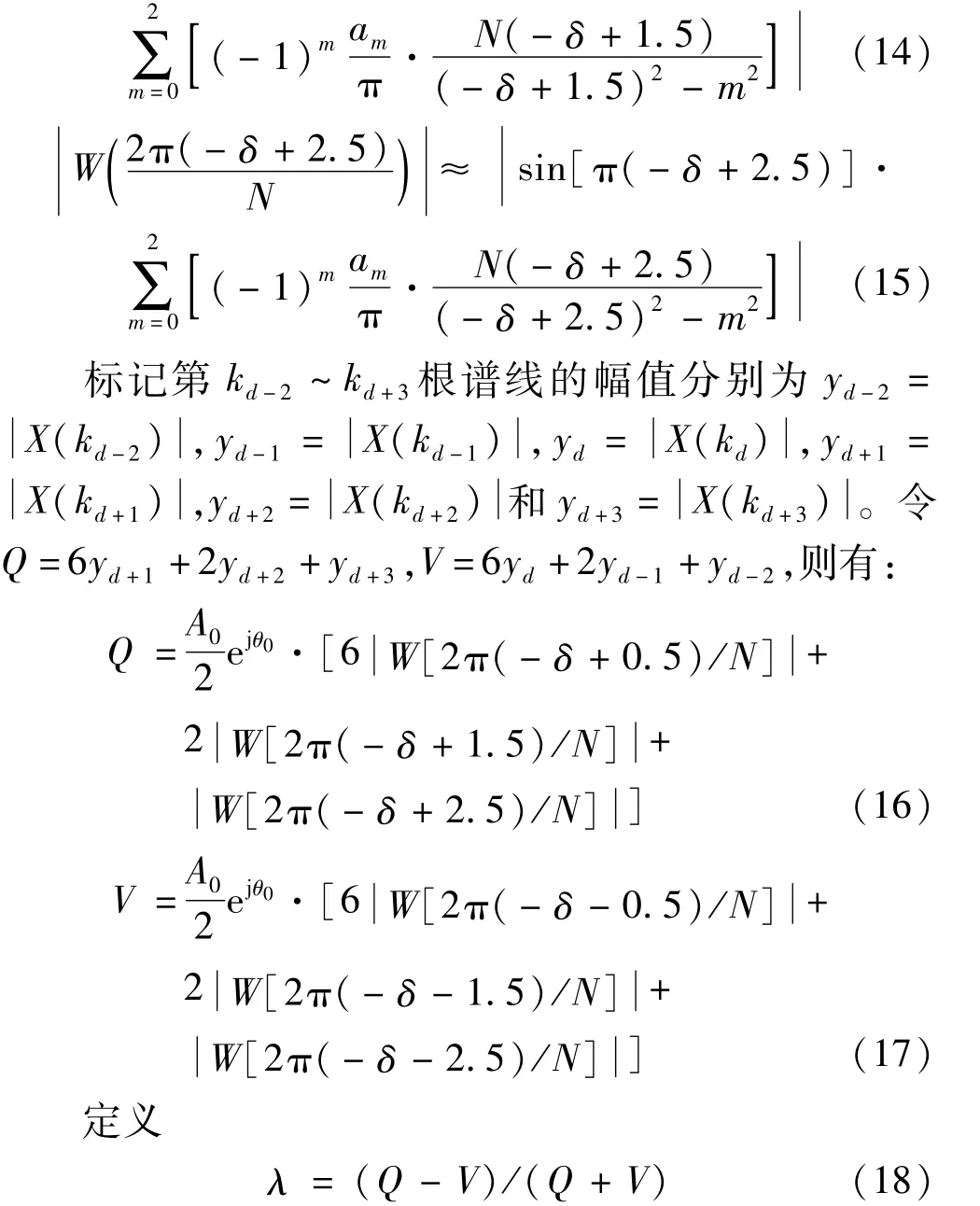
标记式(18)为λ=g(δ),则从理论上可以通过求反函数得到偏移量的计算表达式δ=g-1(λ),其中,g-1(λ)表示λ的反函数。由于表达式过于复杂,因此要获得δ的闭式解非常困难。为了降低实现的复杂度,本文提出一种基于多项式拟合求解表达式g-1(λ)的方法。具体而言,在区间(-0.5,0.5)内取δ的一组具体值,并利用式(18)计算得到相应的函数值,在此基础上利用多项式曲线拟合方法即可得到δ=g-1(λ)的函数逼近式,进而得到信号参数的修正公式。考虑到精度和复杂度问题,本文设定拟合多项式的最高幂次数为7。将式(16)和(17)代入式(18),则利用数值计算软件可方便地得到g-1(λ)的多项式拟合表达式:

相应地,信号频率的修正公式为:

幅值修正公式为:
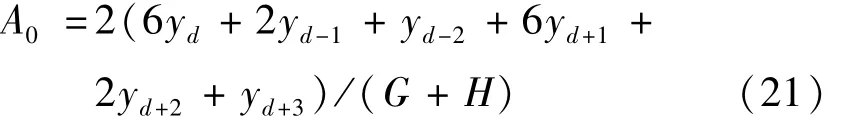
式中,


设f(δ)=2N/(G +H),类似地利用多项式拟合方法可以得到f(δ)的表达式为:
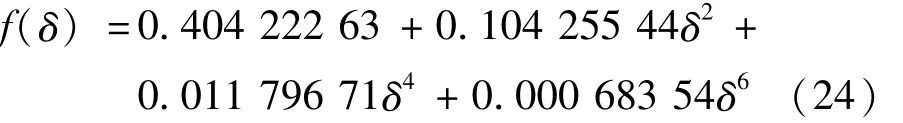
由此幅值修正公式可以简化地表示为:

相应地,信号相位的修正公式为:

3 仿真实验分析
为了验证本文所提算法的有效性,对信号用本文算法、直接FFT分析和加Hanning窗分析3种方法进行实验对比。假定一个由基波、间谐波和谐波组成的复合信号:
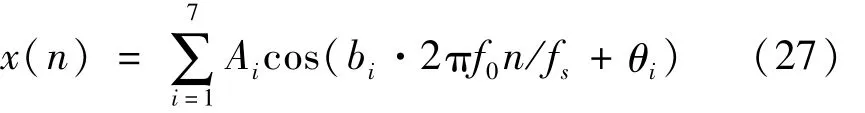
式中,基波频率f0=50.2 Hz;采样点数N =1 024;采样频率fs=1.5 kHz。幅值和相位的具体参数如表3所示。

表3 仿真实验参数设置
对信号分别进行FFT处理和加Blackman窗后信号的幅度谱如图2和图3所示。从图2中不难看出,对谐波直接进行FFT处理会出现较严重的频谱泄露。而从图3不难看出,对信号预先进行加Blackman窗处理后再进行FFT频谱分析,其幅度谱中具有较大幅值的谱线分量仅集中在真实频率附近的少数几根谱线上,而远离真实频率的谱线幅值迅速衰减为很小的值,故加Blackman窗对频谱泄露的抑制效果明显。

图2 利用FFT算法得到的幅度谱

图3 利用本文算法得到的幅度谱
利用FFT算法、加Hanning窗算法、本文算法对信号进行参数估计的结果如表3~6所示。不难看出,在上述3种算法中,基于FFT的方法具有最差的参数估计精度。与此同时,对信号中的谐波和间谐波的参数进行估计时,尽管加Hanning窗方法和本文所提算法都可以提高其精度,但是总的来说本文算法相比加Hanning窗方法具有更高的谐波参数估计精度。

表4 频率估计相对误差对比

表5 幅值估计相对误差对比

表6 相位估计相对误差对比
4 结 语
本文提出了一种基于Blackman窗的六谱线谐波分析算法,该算法利用Blackman窗和六谱线插值结合的方法来抑制频谱泄露和减小栅栏效应带来的影响,在此基础上给出了信号频率、幅值和相位参数的估计公式。经过仿真实验对比,新算法可以有效提高谐波和间谐波的参数估计精度,其精度比FFT算法和加Hanning窗算法的精度有了显著提高,在算法的实现复杂度和估计精度上达到了较好的平衡。

