大功率推板式波浪生成实验系统的建模分析
吴勇平, 邹铭轩, 熊城炜, 倪钱盈, 徐巧宁, 刘 毅
(浙江大学宁波理工学院,浙江宁波315100)
0 引 言
恶劣海况下,现场工程平台和装备事故频发,促使其在试验设计阶段要求对工程平台和装备施加更为真实的波浪冲击,对模拟试验准确度的要求也逐渐严格。波浪生成技术是一项在船舶、水利以及海洋工程等领域重要的基础试验技术,通过在试验水池中生成不同的波浪,可以模拟实际波浪对船舶、海洋装备等其他物体的影响[1-2]。
波浪生成装置中推板的振幅和频率分别由波浪的波高和波长决定[3-4]。大功率电动机常应用于波浪生成装置,但是其存在重载情况下频繁正反转和高换向频率下摆动幅度不高等问题[5]。为了满足波浪生成系统中对高能量、高速度、高位移控制的需要,电液控制技术作为解决大功率波浪模拟存在问题的技术常被国内外大型波浪生成装置所采用,但是,由于系统原理的限制,其推板的运动频率和振幅无法同时实现连续可调,导致现有的波浪生成装置在一定频率范围内推板的振幅并不能进一步得到提高,制约着波浪模拟水平的提升。为使此类驱动系统实现更高的流量、推力和频率,学者们对大推力、多缸、高频的电液振动装备进行了研制,出现了许多新型电液控制技术[6-8]。同时,许多学者也在不断致力于研发新的控制元件来满足具体工程要求。郝建功等[9]利用转阀结构提高了装置的波动频率,并应用于冶金和煤炭等行业。阮健等[10]提出了一种新型高频电液激振器用于大功率液压振动台,并对典型波形的控制与实现进行了研究。其他类似的研究进展还有浙江大学研制的回转直动式电液伺服阀和高压大流量平衡台阶式液压转阀[11-13]、转轴式液压转阀[14]以及单级转阀用于大功率变频振动装置[15-17]。但是,目前的研究仅局限于电液控制式传统方法,对于推板式波浪生成的研究还鲜有报道。
本文针对大功率波浪模拟的需求,对电液控制式波浪生成新方法和控制系统进行了建模和数值分析,以期为相关装备的开发和结构优化提供经验。
1 波浪生成实验系统工作原理
图1所示为波浪生成实验系统原理图,系统主要由双作用伺服缸、双自由度转阀、比例溢流阀、电液比例恒压柱塞泵等部件组成。双自由度转阀的工作原理如图2所示,阀芯有4个结构一样的台肩,一端通过联轴器与伺服电机连接实现阀芯的旋转换向;另一端通过与直线电机连接实现阀芯轴向移动,从而控制阀芯油口的进出流量[10]。伺服电机转速的变化使得液流不断换向,实现伺服缸往复运动控制。该方法可以通过调节变量液压泵的排量机构、混合式直线步进电机和伺服电机控制,能够简单地生成各种频率和波幅的规则波浪。
2 波浪生成实验系统数学建模
波浪生成实验系统等效原理分析如图3所示。
假定流体为理想流体,只考虑稳态情况,系统供油压力ps恒定,p0为电液系统回油压力,供油量为qs,负载流量和压力分别为ql和pl,伺服缸两腔压力分别为p1和p2。且p1-p2=po,p1+p2=ps。伺服缸负载流量与阀口流量关系式为ql=qv2-qv1或ql=qv3-qv4。依据流经节流孔的流量公式[18],可推导通过阀芯阀口1~4的流量方程表达式分别为:
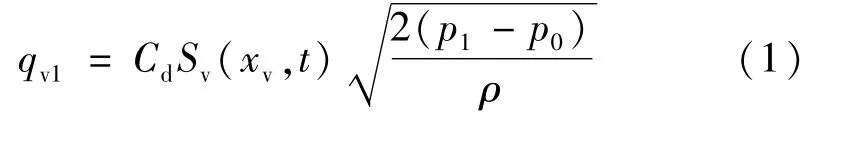

图1 波浪生成实验系统原理图
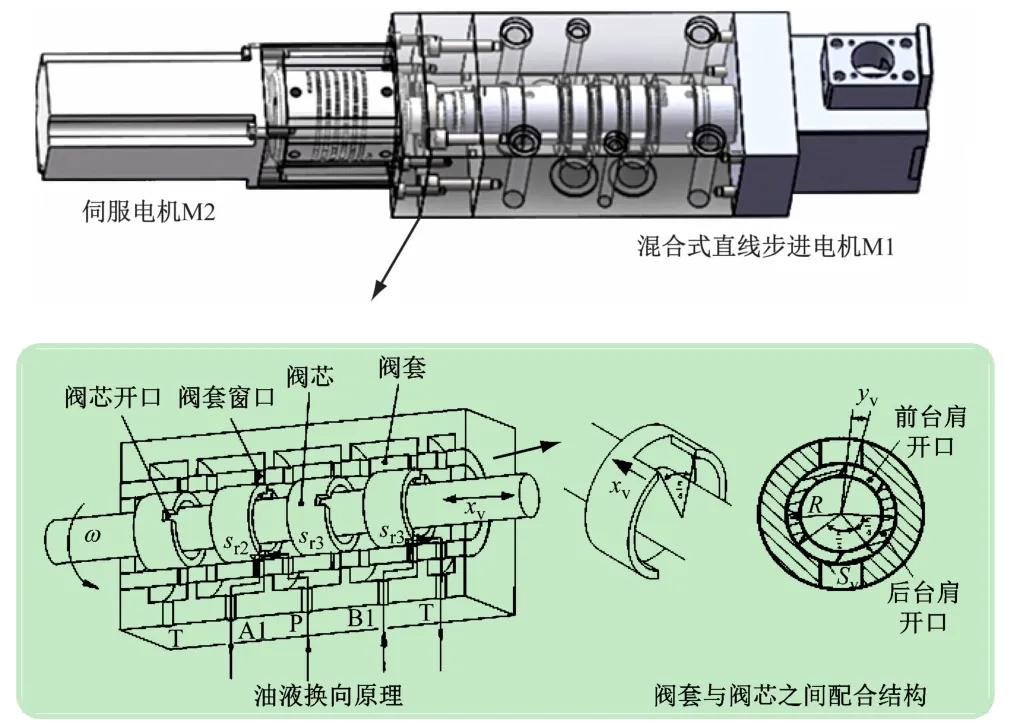
图2 电液控制阀的工作原理图

式中:Cd为流量系数;ρ为流体密度;Sv为导通面积。
如图2右下角部分所示,xv为阀芯油口轴向尺寸,假设每个台肩周向均匀开设2个阀口,前后台肩阀口均匀对称分布,阀芯和阀套的开口均设计成矩形,则阀口过流面积关系式为:

令yv1和yv2分别为前台肩开口周向尺寸和后台肩的开口周向尺寸,定义yv1从关闭到最大,然后从最大至关闭,接着进入后面台肩下一个开口yv2,yv2也是从关闭到最大,然后从最大至关闭。假定阀芯的转动频率为f,则阀芯的转动角速度为ω1,R为阀芯台肩半径,yv1和yv2表达式可以推导为:

由图2可知,阀芯旋转1圈,油液换向两次,使得伺服缸能来回振动两次,则伺服缸的工作频率与阀芯旋转频率的关系为fj=2f。
假设油温和体积弹性模量为常数,伺服缸不存在泄漏,转阀与伺服缸的连接管道短,粗且对称,忽略管道中的各种损失,伺服缸两个工作腔内各处压力相等。
流入伺服缸左腔的流量为
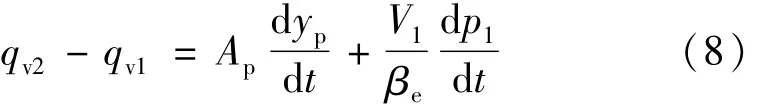
从伺服缸右腔流出的流量为
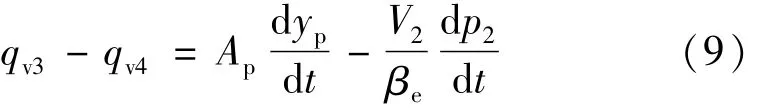
式中:βe为油液的体积弹性模量;V1为进油腔容积,V1=Vo1+Apyp,Vo1为伺服缸初始容积;V2为回油腔容积,V2=Vt-(Vo1+Apyp),Vt为伺服缸总容积。
伺服缸的输出力和负载力的平衡方程为

式中:Ap为伺服缸活塞有效作用面积;yp为伺服缸的运动位移;mt为等效质量;Bc为总阻尼系数;Kl为总弹簧刚度;Fl为水作用在推板上的力。系统主要受质量惯性力和水作用在推板上的力的因素,其他力的因素影响较小,实际计算分析时,忽略其他力的影响。
如图3所示为波浪生成模型图,假设d为水深,距池底d1、d2处板的振幅分别为e1、e2,水面处的振幅为e,k为波数,k与波的角速度ω满足弥散公式ω2=gktanh kd,且ω =2πfj。由势流理论可知[19],即处于不同周期时板前波浪波幅a0与推板振幅e的关系为:
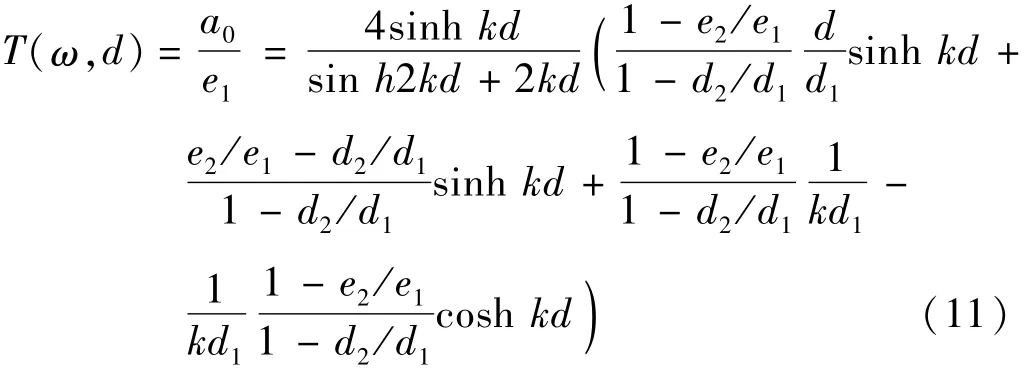

图3 波浪生成模型图
对于推板式系统而言,e1=e2=e,d1=d,d2=0,且前面所建模型的原理,yp同于e,则:
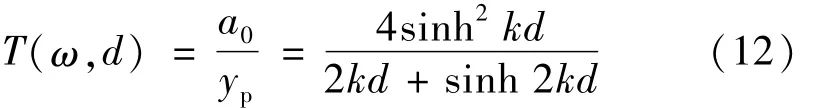
3 数值分析
如图4所示系统的总模型图,依据上节所推导建立的数学公式,在Simulink软件中建立系统的模型来求解并进行分析。首先将整个系统模型分解为若干个子系统模型,在确认各子系统求解模型正确后,再将各子系统输入输出关系相关联求解系统的总模型。通过设定波浪生成系统中的主要结构参数,在运行求解时,调整主要输入控制参数的大小,将得到不同控制参数对波浪生成的规律,为波浪生成装置实际操作实验时提供理论支持和参考依据[16,17]。波浪生成系统的主要参数如下:ps=21 MPa,D0=90 mm,xv=4,8,12 mm,d0=45 mm,yvmax=12 mm,Ap=51 ×10-4m2,Cd=0.62,V1= 76 × 66-4m3,R = 15.5 mm,V2= 76 × 6-4m3,ρ =870 kg/m3,d =4 m,βe=800 MPa,mt=600 kg。水力传递关系的对应参数如表1所示。
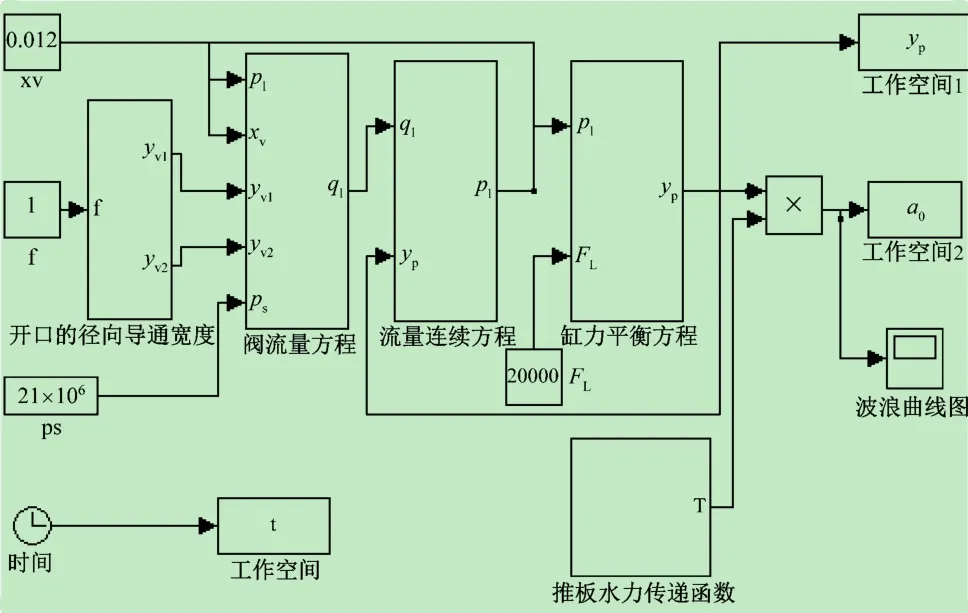
图4 系统的总模型
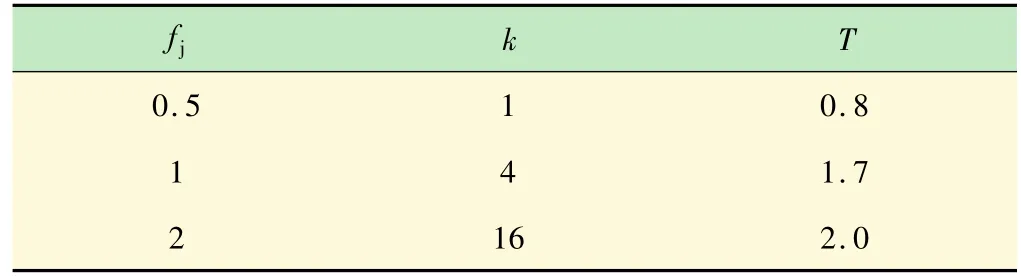
表1 水力传递关系对应参数
图5、6 所示分别为不同xv下的yp—t,Sv—t和ao—t的曲线图。由式(5)可见,Sv的大小主要由xv和yv所决定,阀芯旋转速度变化主要影响yv变化,进而影响Sv的变化,而xv大小变化直接决定Sv峰值的变化,这种变化又会直接影响yp和ao,因此xv是影响伺服缸的运动幅值大小的一个重要影响因素,xv越大,yp和ao也越大,且在21 MPa的系统供油压力和1 Hz推板造波运动频率的同等条件下,在xv分别为4,8和12 mm情况下,Sv同比例增大,yp和ao也同比例增大。在xv为12 mm情况下,最大波高波幅达到了1.35 m。

图5 不同xv下的Sv—t,yp—t曲线图

图6 不同xv下的ao—t曲线图
图7 、8所示分别为不同频率下yp—t,ao—t的曲线图。从图7可以看出,当f=0.25 Hz时,即fj=0.5 Hz,yp的变化周期是2 s,yp的最大值为1.35 m,当f=0.5 Hz时,即fj=1 Hz,yp的变化周期是1 s,yp的最大值为0.675 m,当f=1 Hz时,即fj=2 Hz,yp的变化周期是0.5 s,yp的最大值为0.337 m,说明f越大,yp的大小和变化周期相对越小,且成比例缩小。从图8可以看出,波浪生成装置不同的工作频率对产生波浪的运动频率和波高影响很大,在fj=1 Hz的时候,最大波幅到了1.11 m。若要进一步提高模拟波浪的能量和增大波高,在其他各个条件不变的情况下,可以通过增大阀口轴向开口尺寸或控制电液比例泵的供油压力,减少油液溢流量来进一步实现更高波浪的生成。
4 结 语

图7 不同频率下的yp—t曲线图

图8 不同频率下的ao—t曲线图
本文针对大功率波浪模拟的需求,对电液控制式造波新方法进行了建模和分析。结果表明:同等条件下,阀芯油口轴向尺寸越大,推板的摆幅和波浪波幅越大;阀芯旋转运动频率越大,推板摆幅的大小和变化周期相对越小。表明新的波浪生成实验系统易于生成调试各种所需的规则波浪,新系统能够实现在一定频率范围下推板的摆幅进一步提高,从而实现更大波浪波高。通过简单地控制就能实现大功率规则波浪的生成,使得进行波浪模拟研究和实验操作过程更为方便。研究结果对指导大功率推板式波浪生成实验系统设计和验证实际新系统的动态性能具有重要意义。

