例谈三角函数中参数ω、φ的取值范围的求解

谢建宁

(福建省福州第十八中学 350001)

在高三复习中，各级各类模拟试题中经常出现一类求函数y=Asin(ωx+φ)+B的参数ω、φ的取值范围问题，主要考查三角函数知识的应用，以及考查学生逻辑推理、数学运算、直观想象等核心素养.此类问题对许多学生是一难点，学生往往无从入手，或者因不明算理而陷入繁琐的运算当中，花费大量时间却不得正解. 本文拟通过归类解析的形式说明这类问题的解法，以期帮助读者理解、掌握其内在规律、特点.

一、和单调性有关的题型

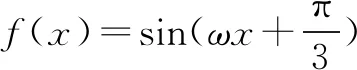
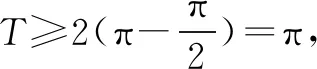
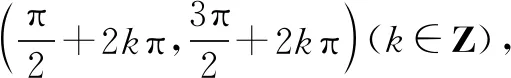
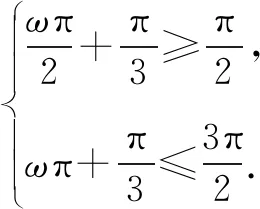
故选B.

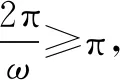
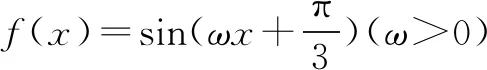
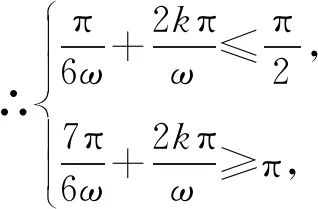
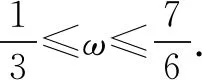
故选B．

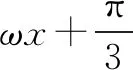
反思三角函数是周期性函数，有无数个单调递减区间，如何选择恰当的区间来套给定区间是解决问题的关键，需要从题中挖掘相关条件，比如：ω的大致范围等.

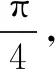
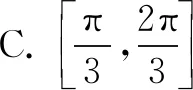
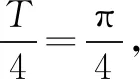
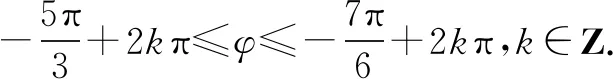
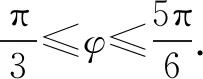
故选B．

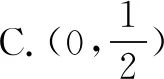
分析函数f(x)在区间[π,2π]内没有极值点，等价于函数f(x)在区间[π,2π]内单调.

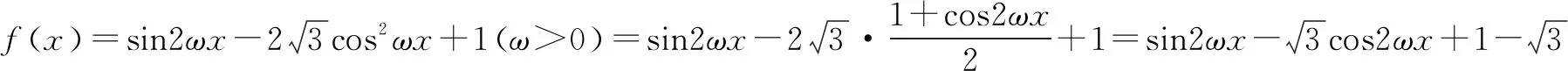
∵f(x)在区间(π，2π)内没有极值点，

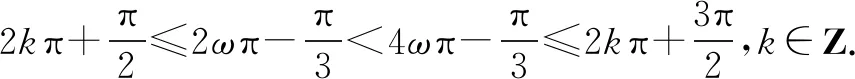
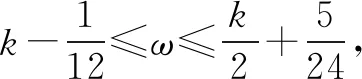
又∵f(x)的最小正周期T≥2(2π-π)=2π，从而0<ω≤1.

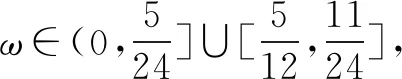
点评例3有条件可知f(x)在给定区间严格单调，可以是单调递增，也可以是单调递减.

二、和最值有关的题型

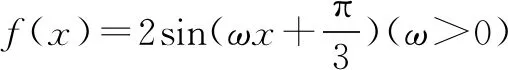
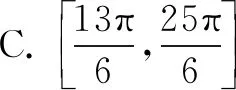
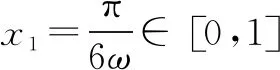
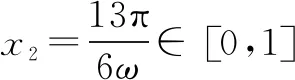
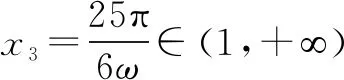
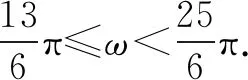
故选C.

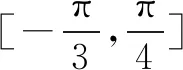
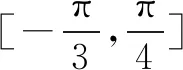
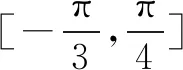
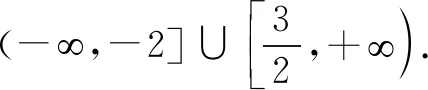
点评此题易忽略对ω两种情形的讨论.

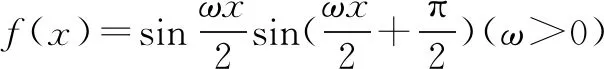
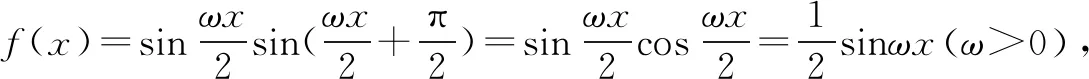
∴函数f(x)为奇函数.

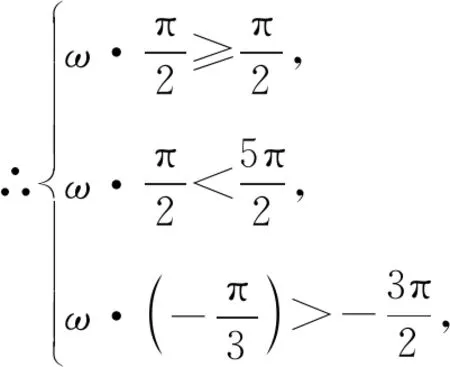
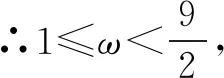
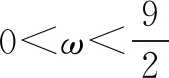
故选C.

点评我们知道，单调函数在闭区间内必有最大值，所以此题有两种可能，学生往往会忽略第二种可能.

三、和零点或对称性有关的题型

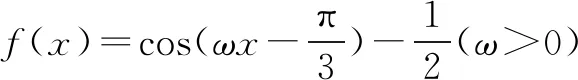
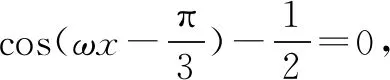
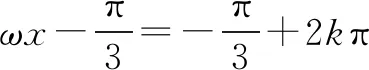
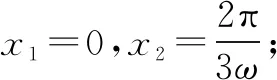
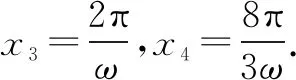
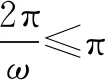
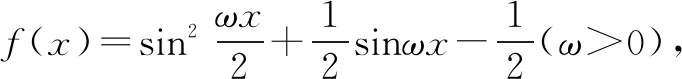
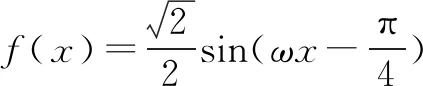
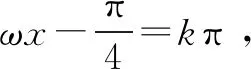
假设f(x)在区间(π,2π)内有零点,

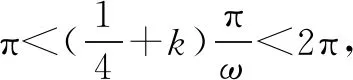
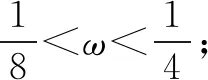
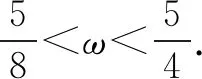
点评此解法先假设(π,2π)有零点的ω的范围，从而得出(π,2π)没有零点ω的范围，正所谓“正难则反”.

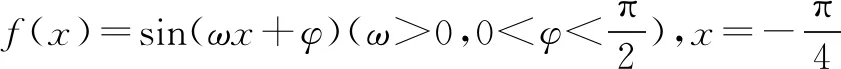
A．11 B．9 C．7 D．5

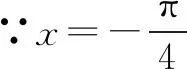
即ω=2n+1(n∈N).

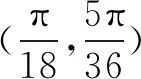
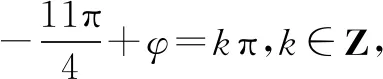
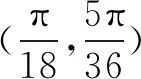
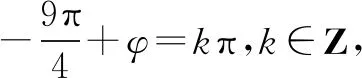
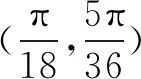
故ω的最大值为9，选B．