求解一对解三角形中的最值问题
2020-08-24 04:41甘志国
数理化解题研究 2020年22期
甘志国
(北京市丰台二中 100071)
题目设△ABC的三边长分别是a,b,c,p,q,r均是已知数且q+r>0,pq+pr+qr>0.
(1)若pa2+qb2+rc2=s,则△ABC面积的最大值为____;
(2)若△ABC的面积是S,则pa2+qb2+rc2的最小值为____.
解法1 设△ABC的长为c的边所对的角是C.由q+r>0,pq+pr+qr>0,可得(p+r)(q+r)=pq+pr+qr+r2>r2≥0,p+r>0.
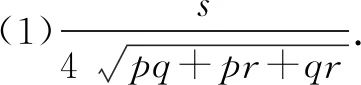
由余弦定理及均值不等式,可得
s=pa2+qb2+rc2=pa2+qb2+r(a2+b2-2abcosC)
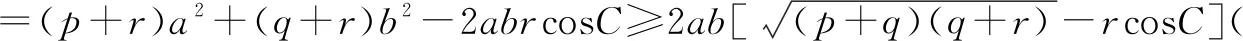
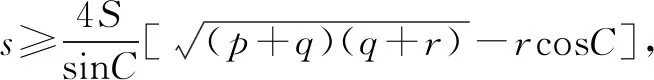
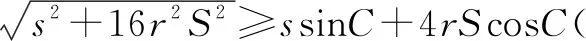
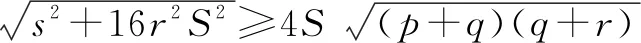
即当且仅当
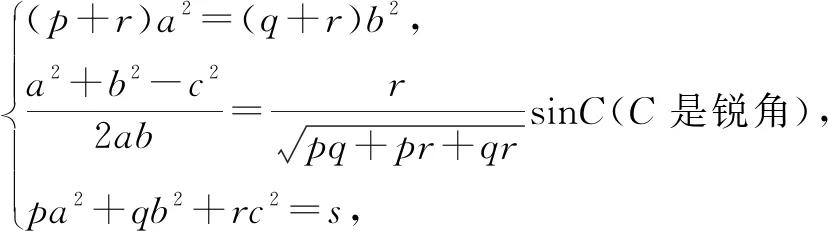
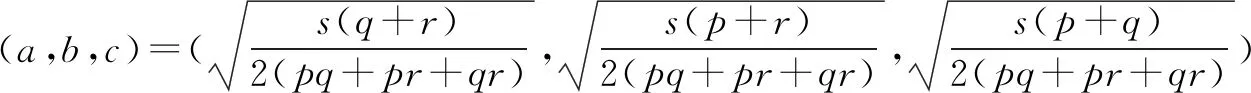
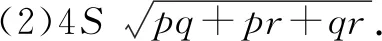
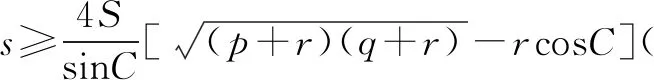
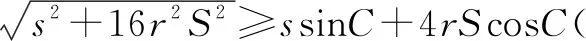
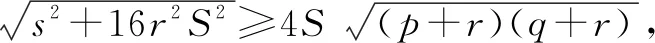
还可得当且仅当
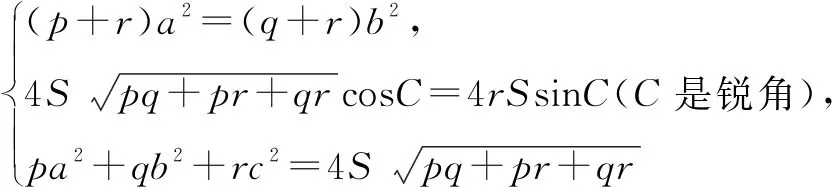
即当且仅当
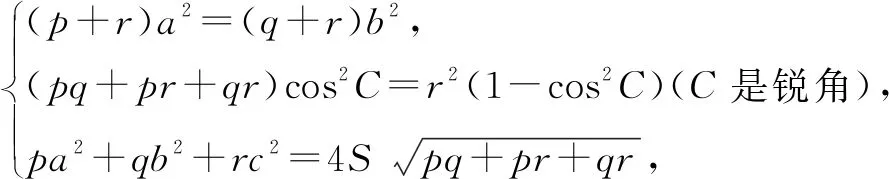
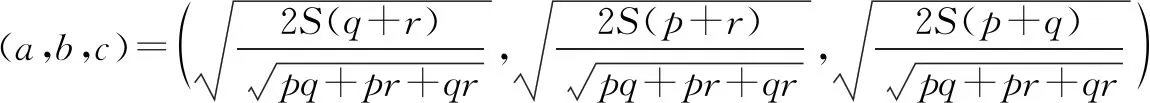
解法2 设BC=a,CA=b,AB=c,△ABC的面积为S.


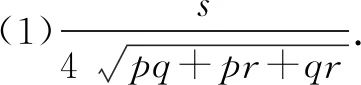
由两点间距离公式,可得
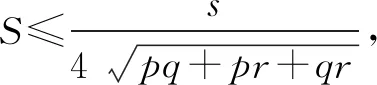

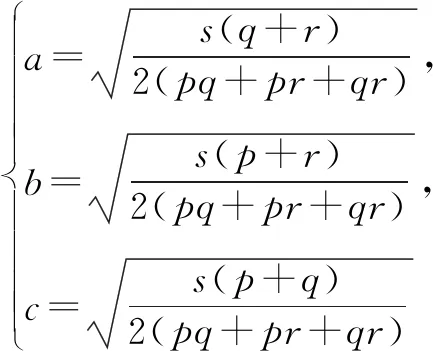
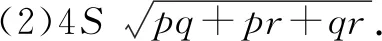
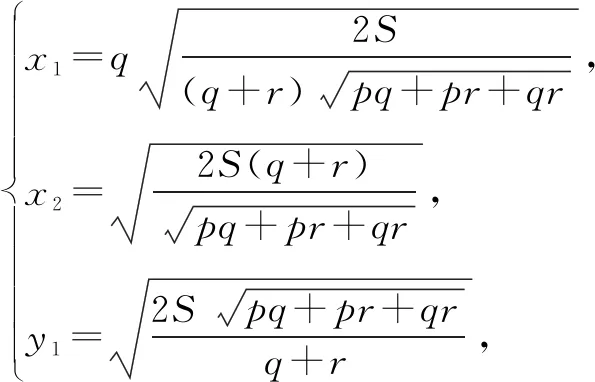
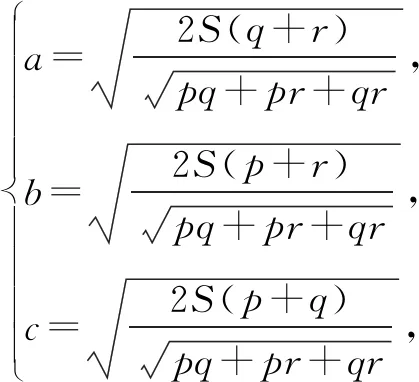
猜你喜欢
中国名牌(2021年10期)2021-10-21
河北理科教学研究(2021年2期)2021-08-18
中等数学(2021年1期)2021-07-23
音乐天地(音乐创作版)(2019年10期)2020-01-06
消防界(电子版)(2018年15期)2018-02-18
环球人文地理(2017年5期)2017-05-26
商(2016年35期)2016-11-24
学苑创造·B版(2015年11期)2016-01-13
中学生数理化·七年级数学人教版(2014年1期)2014-06-20
中国工程咨询(2012年8期)2012-02-14

