例谈条件极值在多元函数最值问题中的应用

余铁青

(广东省中山市桂山中学 528463)

一、引言

笔者最近在统计高考数学考点时经常发现多元函数在考查，并且在近几年的全国数学联赛预赛中考查频率较高.而实际情况是大部分考生做惯了单变量的函数最值问题，一般容易联想到运用代入法，换元法或者导数的方法进行处理，但通过实际运算发现用这种方法处理起来是十分困难的.在高考数学考试大纲里面明确要求要考生进一步培养的潜质，这也导致了大学部分学习的内容渗透到高中进行隐蔽性的考查.这就直接导致了高考数学和竞赛数学中越来越多的考查学生迁移发现的能力.笔者基于此去翻阅了华东师范大学数学系主编的数学分析教材，发现我们利用条件极值和拉格朗日乘数法来解决多元函数最值问题是行之有效的.假如不与学生介绍此类做法会导致大家运用常规的方法进行处理，效率十分低下，得分少，甚至不得分.那么我们系统性，程序性地处理这类问题就显得很有必要了.

二、基本概念介绍

1.偏导数

二元函数当固定其中一个自变量时，它对另一个自变量的导数称为偏导数，定义如下：

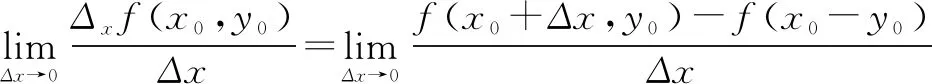
2.拉格朗日乘数法(Lagrange multiplier)

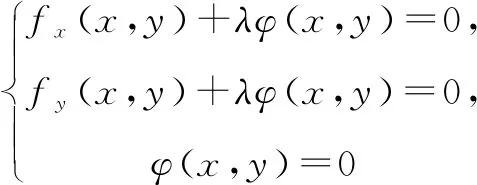
3.黑塞矩阵(Hessian Matrix)

我们称(x0,y0)为稳定点，再根据黑塞矩阵正定，负定来判定是极大值点还是极小值点.

三、真题应用

例1(自变量无限制条件题型)

若x,y∈R，求f(x,y)=x2+2xy+4y2+x+2y的最小值.

引理(截取)在二元二次函数

f(x,y)=ax2+2bxy+cy2+dx+ey+g中，设Δ=ac-b2,则有：

若Δ>0,当a>0时，f(x,y)在点p(x0,y0)取到最小值.

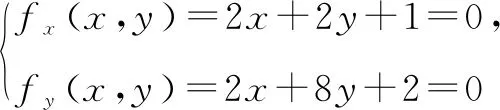
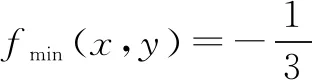
对比引理，此题中a=1,b=1,c=4,显然Δ=ac-b2=3>0，所以解答正确.

说明完整引理来源于1990年昭通师专(现昭通学院)数学系教师饶克勇老师发表的《二元二次函数的极值公式》)

例2(自变量有限制型题型)

(浙江2014年高考题文科)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1，则a的最大值为____.

解构造拉格朗日函数：

L(a,b,c,λ,μ)=a+λ(a+b+c)+μ(a2+b2+c2-1)，

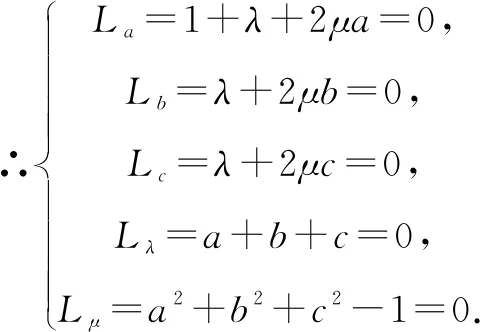
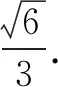
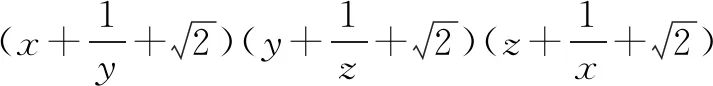
方法1(常规法)

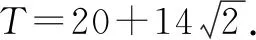
由均值不等式显然有

显然这种做法很难想到，尤其是第一步为什么要取三个自变量相等且同时为1.

方法2(偏导法)

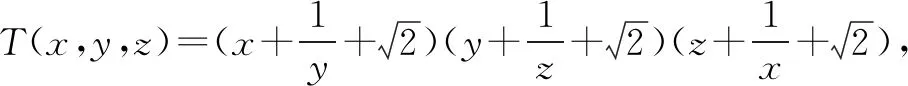
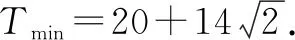
对比发现这样处理起来远比利用不等式简单，而且辐射面扩大，能够较好地照顾到基础中等的同学.

写在最后：很多一线教师抱怨高等数学内容的学习对于中学的教学没有太大的作用，实际上是因为没有真正把两者进行比对分析，发现内在的必然联系，才造成认为高等数学在初等数学里面没有应用的错觉.笔者认为必须在教学中要经常反思，以促成教师掌握以高观点的角度看问题的思维意识和情感态度.