基于Copula函数的股票市场风险溢出网络特征研究

任英华，赵婉茹，罗良清

(1.湖南大学 金融与统计学院，湖南 长沙 410079；2.江西财经大学 统计学院，江西 南昌 330013)

一、引言

20世纪90年代以来世界各国金融危机频发，尤其是2008年次贷危机导致的全球性金融危机，引发了各国监管部门对“微观审慎政策”的重新审视，强调金融风险需要进行宏观审慎监管。复杂的股票市场因其标的资产价格的不确定性、投机行为等可能存在的高风险问题而备受关注。以往研究大多关注单一股票市场风险的计量和监测，关于股票市场风险传染的网络化问题尚未引起足够重视。在金融一体化与混业经营的模式下，各国股市已然形成了一个错综复杂的网络，一国股市受到一定程度的负面冲击时容易滋生风险，在“多米诺骨牌”效应下通过外溢渠道迅速波及整个金融市场。鉴于此，构建全球主要股票市场间风险溢出网络，全面监测各国股市风险传染的动态变化，识别风险溢出中心、排查潜在风险隐患、降低风险传染概率，对于中国实施宏观审慎监管具有重要意义。

目前，国内外关于风险(VaR)及风险溢出(CoVaR)效应的研究，大多采用时间序列的分析方法，以下三类最具代表性：一是波动率方法，可以追溯到Engle的Arch类模型，推广到Garch、Dcc-Garch等方法[1]。Girardi等基于Dcc-Garch模型估计时变CoVaR，揭示系统性风险的动态变化过程[2]。李丛文等根据Garch-时变Copula-CoVaR模型度量影子银行对商业银行的动态风险溢出效应[3]。二是分位数回归模型。Engle等首次提出条件自回归分位数模型(CAViaR)估计时变VaR[4]。Adrian等使用分位数回归对CoVaR模型进行估计，奠定了CoVaR模型后续研究的基础[5]。分位数回归模型无需指定数据生成过程，但缺乏相关分布假设导致统计推断在数据稀疏的尾部具有不稳定性。三是极值理论(EVT)测度风险[6-7]。常用的极值理论有超门限阀值法(POT)和分块样本极大值模型(BMM)，主要关注序列尾部的条件分布，但扩展到动态的研究较少。

鉴于各国股票市场的联动性不断加强，已然形成一个整体。除采用时间序列分析方法外，从网络拓扑的角度对股票市场的关联性与溢出性进行拓展的研究备受关注。大量文献从标的资产收益率的关联性出发，根据相关系数或引力矩阵采用最小生成树算法、平面最大过滤图算法以及阀值法等建立网络，揭示股票市场的联动性与相关性[8-10]。黄玮强等将绝对相关系数矩阵转化为距离矩阵，采用最小生成树算法、平面最大过滤图算法构建中国上证与深证的股指收益率的关联网络，发现关联网络内节点之间的相关性服从幂律分布[11]。Wang等指出用绝对相关系数表征股票市场间的相关性，并没有剔除其他股市的影响，无法反映二者之间的净相关关系[9]。并且，Engle认为绝对相关系数在股票波动率较大的子样本期(如金融危机期间)是有偏的[12]。

目前，国内外文献从网络拓扑角度展开的风险溢出效应研究尚处于起步阶段[13-14]。国内文献大多借鉴Diebold等的方法，运用广义向量自回归模型依托预测误差方差分解构建溢出指数，结合网络拓扑结构进行拓展研究[15-17]。然而，一方面基于该方法计算的溢出指数多为波动性溢出，与真正的风险溢出(CoVaR)有所区别。另一方面，该方法需要设置滚动窗口，如果窗宽过短，时变溢出的异常值容易增多；如果窗宽过长，可能无法捕捉一些突变情况。此外，窗宽的存在也会使时变溢出的计算结果损失一个窗宽长度。

有鉴于此，本文试图从以下方面进行拓展研究：在研究对象上，以全球30个主要股票市场为例，从宏观角度考察全球股市间的风险溢出关系。值得注意的是，不同于以往集中在年度和月度层面的研究[13]，本文将蕴含丰富信息的日度交易数据应用于风险传染的研究中，更能满足实际需要。在研究思路上，以网络化的视角探讨股票市场风险传染关系，采用动态和静态相结合的方式分析风险溢出网络的拓扑结构和板块特征。在研究方法上，Dcc-Garch-Copula-ΔCoVaR模型通过引入时变 Copula函数度量股票市场间的动态相依性，从而更有效地刻画金融市场风险溢出的变化情况。根据各时点的风险溢出关系建立的动态网络，不仅能够避免人为设置窗口的偏误，而且有助于监测网络特征及演化模式，捕捉行为异常的时期，在金融风险监管，系统风险评估等领域具有重要的应用价值。在构建全局静态网络时，由于时变风险的频繁波动和噪声干扰极大影响了全样本网络连接的准确性，本文摒弃以往文献的网络构建方法(例如，MST和PMFG)，首次从小波分解的角度提取风险溢出序列的均值、趋势、波动以及周期信息，得到反映风险溢出特征的综合指标，作为网络的连边。这种方法不仅能够最大限度地减小信息损失，更能表征整个样本期间风险溢出的综合特征。

二、研究方法

(一)时变Dcc-Garch-Copula-ΔCoVaR模型

风险价值(VaR)被视为标准的市场风险衡量指标，是指投资组合在给定的置信区间内的最大可能损失，与分位函数密切相关，可结合波动率法(Garch)、极值理论(EVT)和条件自回归分位数模型(CAViaR)等方法测度。Dcc-Garch-Copula-ΔCoVaR模型将Garch模型和Copula函数结合到VaR框架中。其中，Dcc-Garch模型能够捕捉股市波动的典型特征，如厚尾性，Copula函数可刻画两国股票市场间的相依结构，二者结合可有效衡量股票市场的时变风险溢出。

在采用Copula 函数捕捉股市之间的动态相关结构时，首先需要确定单个国家股票市场的边缘分布，再选取合适的Copula函数来刻画两个国家股票市场的联合分布。为了更好地体现各收益率序列的尖峰厚尾特征，本文选用偏t分布的Garch模型拟合边缘分布。具体过程如下：

首先，对股票市场收益率序列的均值方程建立AR(1)模型，考虑到金融时间序列的尖峰厚尾特征以及波动的非对称性，采用偏t分布的Garch(1，1)模型进行拟合，模型的具体形式如下：

ri，t=c+c1ri，t-1+ei，t

(1)

ei，t=hi，tεi，t，εi，t～SKT(υ，λ)

(2)

(3)

然后，利用Copula函数刻画两个股市收益率的联合分布，根据Sklar对Copula连接函数的描述，它将随机变量的联合分布与边缘分布连接在一起，任意二维联合分布函数都可以灵活地通过连接函数与各自的边缘分布构造：

F(x1，x2)=C(F1(x1)，F2(x2))，∀x1，x2∈R

(4)

(5)

根据信息准则和对数似然函数值选择较优的时变连接函数对两两股市之间的关系进行刻画。由于不同股市间的相依结构不同，选择的Copula函数也有所不同，大多以时变t-Copula函数为主，相应的密度函数如下：

t-Copula函数：

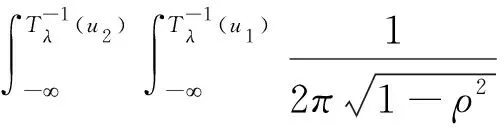
(6)

关于相关系数，本文参考Engel的方法，选择Dcc-Garch模型刻画时变相关系数矩阵[12]：

(7)

(8)

Adrian等将CoVaR定义为一国股票市场发生风险时给其他国家股市带来的风险[5]，其本质上就是当某一国家股票市场处于显著性水平分位点(VaR)时另一国家的条件概率分布的分位数，减去自身风险即为风险溢出ΔCoVaR。

(9)

(10)

(11)

其中，rt是收益率序列，Ft-1是过去时刻的信息。则股市1受股市2的CoVaR1|2应该满足：

C1|2(F1(CoVaR1|2)，q)=q

(12)

可见上述分位数其实就是对密度函数求变上限积分，所以只要得到变量分布的密度函数，就可以计算CoVaR。再根据式(10)即可计算时变风险溢出。

(二)静态、动态风险溢出网络构建

根据复杂网络的思想，伴随资本市场开放，国内与国际业务交叉渗透，地理空间上的限制基本能够克服，一国股市很容易将风险传染给相距遥远的国家，复杂的股市通过相互溢出形成网络。网络中节点为各股票市场，边为成对股市间的风险溢出。通过Dcc-Garch-Copula-ΔCoVaR模型测出全球两两股市间时变风险溢出，任意时点的风险溢出关系均可视为该时点网络的边，采用阀值法(以均值为阀值)过滤风险溢出较小的边，保留较大的风险溢出关系构建复杂网络。依次构建各时点的风险溢出网络，最终形成动态网络。本文构建的动态复杂网络不仅能够分析不同国家之间股市风险溢出的网络特征及其演变过程，而且不需要设置窗口参数，避免人为设置窗口的偏误。

关于整个样本期内静态风险溢出网络的构建，本文首次借鉴戴大洋等运用小波分解提取主成分降维的思想[18]，采用小波多分辨分析提取整个样本期风险溢出的均值、趋势、波动、周期特征，通过熵权法计算权重，得到表征股票市场之间风险溢出关系的综合指标，视作静态网络的边，运用阀值法构建整个样本期风险溢出静态网络。小波分析能够通过滤波器将风险溢出序列分成低频信号和高频信号，从低频信号中提取的均值和趋势特征可更好地反映风险溢出的整体变化，避免噪声和干扰；高频信号能较好地提取时间序列的波动以及周期信息，基于该方法得到的综合指标能有效度量整个样本期的风险溢出效应。

小波多分辨分析是指用一个具有震荡性且能够迅速衰减到零的小波基，通过尺度伸缩以及平移变换逼近某一信号，具体形式如下：

(13)

其中，Wf(a，b)为小波变换系数；f(t)为信号函数，a为伸缩尺度，b为平移参数。

小波周期可以根据小波方差的时序变化得到，小波方差取得最大波峰值对应的就是主周期。小波的方差可以通过小波系数的平均值在b域上求期望得到：

(14)

小波的波动用第一层高频数据(d1)的标准差表示：

(15)

关于风险溢出的“均值”以及“趋势”特征，采用经小波分层后最后一层的低频数据(at)计算。

(16)

(17)

(三)数据描述

依据股票市场数据的可得性以及收益率序列的拟合效果，本文最终确定的研究对象为全球30个主要股票市场，根据地理位置可分为美洲地区，欧洲、中东和非洲地区(EMEA)及亚洲地区(1)其中美洲地区5个，即美国、加拿大、墨西哥、智利、阿根廷；EMEA国家14个，包括奥地利、德国、英国、西班牙、芬兰、比利时、瑞士、荷兰、希腊、捷克布拉格、斯洛伐克、俄罗斯、南非、澳大利亚；亚洲地区11个，分别是中国内地以及香港地区、日本、新加坡、韩国、泰国、菲律宾、印度、以色列、土耳其、斯里兰卡。为有效反映全球股市的基本情况，本文根据“经济基础说”选择了股票市值占全球股市比重大、地理分布涉及较为广泛的30个股票市场进行研究。。股市收益率均是根据股票市场收盘价的对数差分计算得到，数据来源于汤森路透数据库，样本为2000年1月3日至2018年12月4日的股市日度交易数据，共有 4 937个交易日。全球主要股市收益率及其描述性统计见表1。

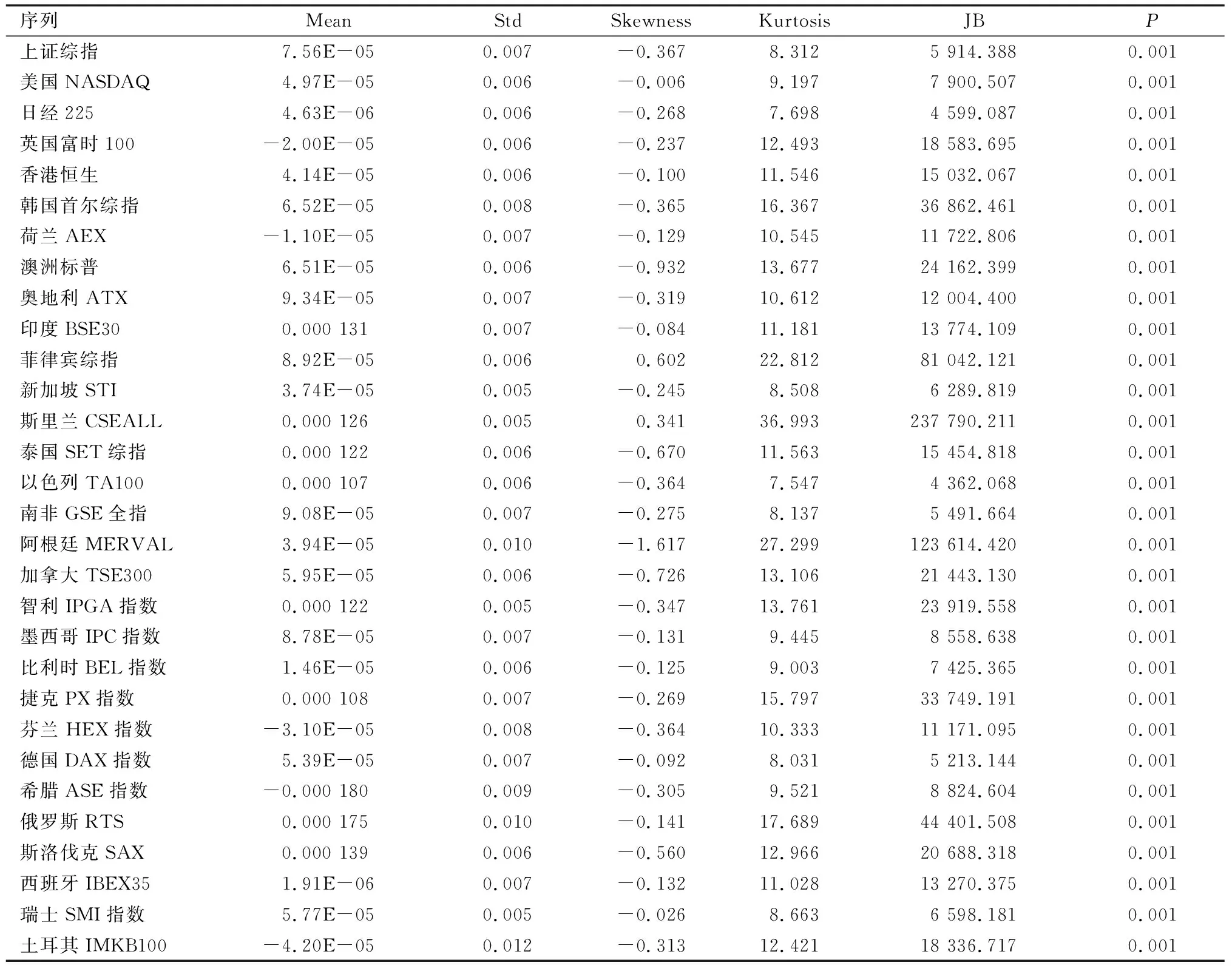
表1 描述性统计

三、实证分析

(一)时变风险溢出的测度结果分析

在进行风险溢出测度前，对各股票收益率序列进行单位根检验，均为平稳序列(2)由于文章篇幅限制，单位根检验结果并未给出，感兴趣的读者可以向作者索要。。从表1的描述性统计结果可知，股票收益率不服从正态分布，具有高峰厚尾特性，因此本文运用偏t分布的Garch模型拟合各个国家股票市场的波动情况。

表2是Garch模型拟合的结果。其中，α为残差平方滞后项系数，β为条件方差滞后项系数，α+β为衰减系数，表示股票市场波动的持续性。结果显示所有股票指数的α+β值均高于0.9，这与李岸等的研究基本一致，说明股票市场在未来存在持续波动。比较各个国家α和β系数发现，中国内地、香港地区以及日本的α系数略低于其他国家，β系数略高，说明中国以及日本股票市场的信息敏感程度低，股票指数的波动主要依靠自身的记忆性。

表2 偏t分布的Garch(1，1)模型的参数估计结果

时变Garch-Copula-ΔCoVaR方法测出30个股票市场的时变风险VaR以及任意两个市场之间的时变风险溢出ΔCoVaR(870个)。限于篇幅，本文仅展示中国内地与香港股市的风险状况(图1)以及其他主要国家对中国股市的风险溢出(图2)，以便中国股市更好地防范他国风险传染。

由图1可知，中国上证综指和香港恒生指数的风险变化趋势大致相同，具有一定的波动性与集聚性。极端波动主要在2007—2009年和2015—2016年两个时间段，这与2008年美国次贷危机引发全球股灾以及2015年中国股灾情况相吻合。其中，2008年金融危机笼罩下的中国香港股市面临的风险更大，遭受的冲击更深，风险由-0.01飙至-0.045。而2015年股灾主要危及内地股市，数次千股跌停及熔断机制的失败给中国内地股市带来了巨大的冲击，风险大幅上升。此外，在2001年末和2016年末到2017年初，还存在两个相对较大的下行波动，中国股票市场风险增大。这与2001年国有股减持、股价急剧下跌以及2016年英国意外脱欧对中国股市的冲击有关。其他时间段比如2013年风险增大，可能与中国国内的“钱荒”有关。这些充分表明极端事件对中国股市的长期稳定发展造成极大的不利影响，而时变Garch-Copula-ΔCoVaR模型能够较好地捕捉股票市场的风险变化。

图2为全球主要股市对中国股市的溢出效应。上图表示中国内地股市受中国香港、美国、英国以及日本股市风险溢出的影响，下图展示了中国内地、美国、英国以及日本股市对中国香港股市时变风险溢出的渐进演变过程。大体而言，风险溢出变化幅度不大，可能是因为剔除了自身风险，只考虑对中国股市的净溢出。不同市场的风险溢出始终为负，说明在不考虑其他市场发生极端损失(风险)的情况下，美国、英国、日本股市发生风险时都会在一定程度上冲击中国股市。另外，中国内地股市受英国股市的风险溢出最大，港股次之，美国第三，日本最小。中国香港股市受美国、英国的风险冲击远大于中国内地以及日本，且风险溢出更为直接和明显，可能与香港地区和美国、英国的经济、贸易等联系更密切有关。

图1 中国股票市场风险时序图

图2 全球主要股票市场对中国股市的风险溢出时序图

(二)静态风险溢出网络

考虑到全球金融市场联系密切，风险溢出途径相互交织，有必要将整个样本期风险溢出关系整体纳入分析框架中，全面考察各个国家的股票市场在全球风险溢出网络中扮演的角色和发挥的作用。在小波提取整个样本期风险溢出的均值、波动、趋势以及周期特征的基础上，运用熵权法赋权(权重分别是0.254、0.235、0.249、0.261)，建立综合指标，用于整体静态网络分析。

由图3可知，风险溢出具有复杂性，彼此之间普遍联系、相互传染，没有任何一个国家是完全“孤立”于网络之外的。进一步分析静态网络的结构特征发现，网络中实际存在的关联数为 514，可能存在的最大关联数是870，网络密度为0.591，说明各个国家之间风险传染的密切程度相对较高。风险溢出网络的关联度为 1，表明全球主要国家金融市场风险传染网络的通达性好，各个国家之间普遍存在溢出，抑制国家之间风险的传染还有很长的路要走。平均聚类系数达到0.710，表示风险传染程度高、传染面广，其中中国的聚类系数只有0.595，表明中国对他国风险传染的程度远低于平均水平。平均最短路径大于1，表明风险在有些国家间并不是直接传染，而是通过中介渠道传染。

图3 静态风险溢出网络图

表3 静态网络结构特征

接下来是各个股票市场的中心性分析，根据 表4 第一列的点出度中心度可以看出，排名前4的国家分别是美国以及三个欧洲国家，即英国、荷兰、奥地利，这与接近中心度出度排名前四的国家一致，说明这些国家处于风险溢出的中心，具有辐射作用，对其他国家存在较多的风险溢出。美国及部分开放的欧洲发达国家风险溢出程度高，这与梁琪等的研究基本一致[19-20，13]。根据第二列入度不难发现，芬兰、俄罗斯、瑞士、捷克以及希腊入度和中心度排名靠前，在整体上受到风险的传染较强，这些国家亦属于欧洲地区，一定程度上表明欧洲地区内部金融风险传染的两极分化现象严重，存在明显的非对称性。可能原因主要有两个方面：第一，尽管同属于欧洲地区，但不同地区的经济基础和金融开放进程存在差异。第二，欧债危机重创欧洲国家，欧元区市场面临的共同风险敞口被进一步放大，容易遭受风险溢出。部分学者，如刘海云等关于节点中心度的研究结果，证实欧元区风险溢出存在非对称性[13]。关于中间中心度，中国内地、奥地利、荷兰以及美国股市位列前四，具有很强的中介性，助力风险传染，加强风险传染网络的紧密性与联通性。其中，上证综指位列第一达到64.3，最容易成为传染的中介渠道。究其原因，上证综指较高的点入度说明容易受到风险传染，“一带一路”的推进加强中国与沿线国家的交流合作，风险容易通过中国这一中介传染给投资环境和金融稳定性较差的国家。

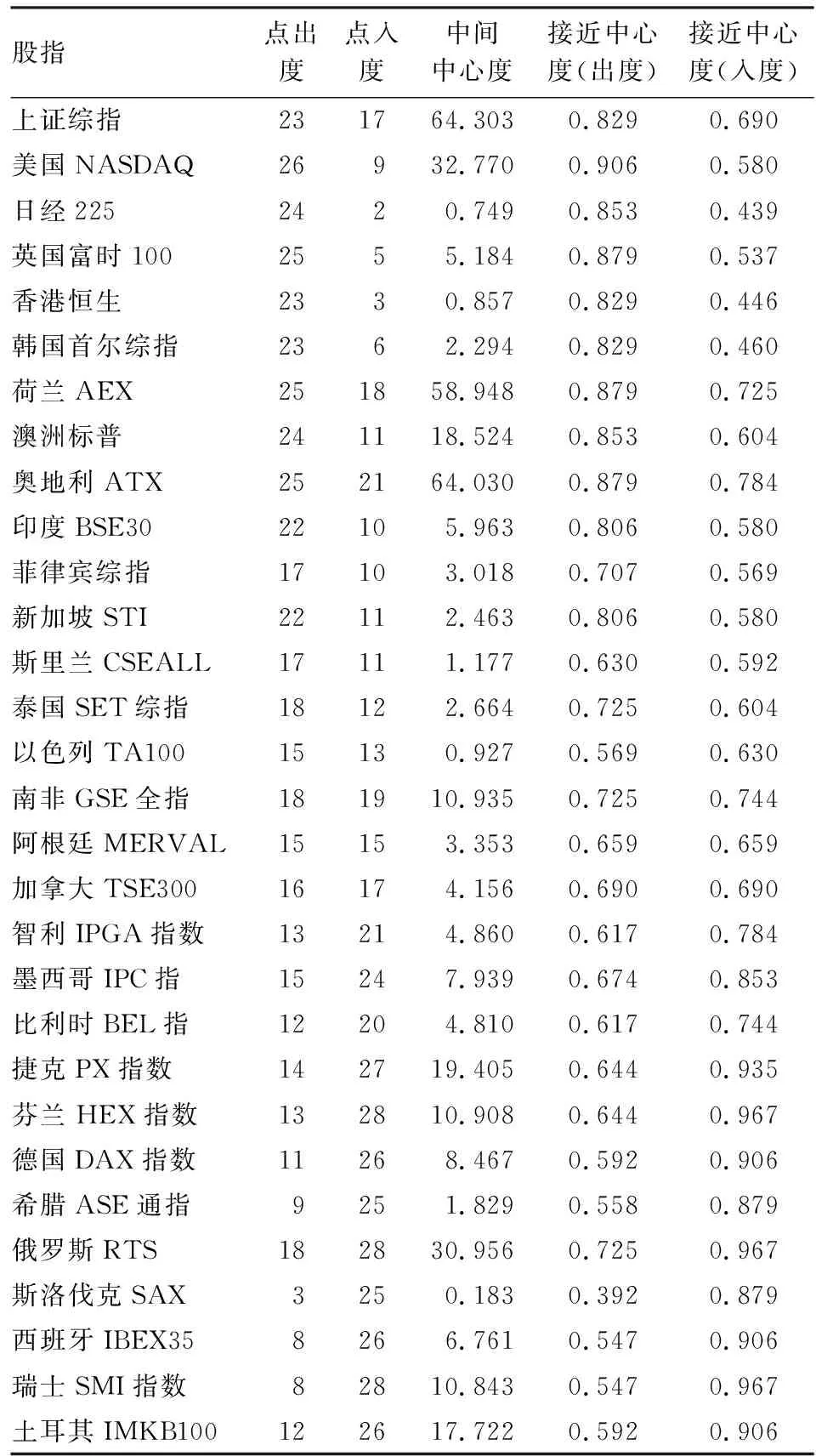
表4 节点中心性分析

通过块模型分析，可得到全球主要股票市场网络的空间聚类特征、溢出关系、地位以及作用等。主要根据股票市场风险溢出网络，采用 CONCOR(Convergent Correlations)方法，选择最大分割度为 2，将30个股票市场地位和作用相近的节点划分为同一个板块，共有4个板块，结果见表5。

从表5可知，在空间溢出整体网络的514个关系中，第一板块成员有8个，分别是美国、奥地利、日本、英国、韩国、荷兰、澳大利亚以及中国香港地区，内部溢出数为23个，溢出关系总数为134个，期望内部关系比例为0.241，实际内部关系比例是0.172，为主溢出板块，该板块主要进行风险传染活动。第二板块成员数有7个，均为亚洲地区，分别是中国、新加坡、印度、菲律宾、以色列、斯里兰卡、泰国，其中内部关系数为28，溢出关系总数为195，期望内部关系比例为0.207，实际内部关系比例为0.144，该板块既传染风险又会受到风险传染，且接受的风险溢出较少，具有中介作用，为经纪人板块。第三板块成员数为 6个，分别是南非、阿根廷、加拿大、智利、墨西哥、比利时，该板块接收关系数为 116 个，其中内部关系数为19个，溢出关系总数为89个，期望内部关系为 0.172，实际内部关系为0.213，为双向溢出板块。第四板块成员数为 9个，分别是捷克、芬兰、德国、希腊、俄罗斯、斯洛伐克、西班牙、瑞士、土耳其，板块接收总数为239个，溢出关系数为96个，期望内部关系比例为0.276，实际内部关系比例为0.646，为主受益板块，该板块接受风险传染的关系数明显高于其进行风险传染的关系数。总体而言，金融风险传染在整体上具有区域性，板块聚类特征明显，主溢出板块的成员地理分布广泛，主要集中在美、欧、亚三大洲，多为金融发达的国家或地区，经纪人板块成员来自亚洲国家，主受益板块成员多为欧洲国家和一些发展中国家。这与梁琪等的研究基本一致，他们认为开放的发达国家对外风险溢出程度最高，开放的发展中国家主要遭受来自外部的风险溢出[19，13]。

表5 金融市场风险传染网络各板块的溢出关系

通过像矩阵进一步考察风险在各个板块之间的溢出与传导机制(见表6)。像矩阵的计算规则如下：根据各个板块的密度矩阵可知整体网络密度为0.582，如果板块的密度大于0.582，就赋值为1；反之赋值为0。由像矩阵可见，第一板块分别对第二和第四板块具有溢出效应；第二板块对其他的三个板块均有溢出效应；第三板块对自身以及第四板块有溢出作用；第四板块仅对自身内部具有风险溢出，大体上具有既集聚又传递的性质。

表6 股票市场风险溢出板块的密度矩阵与像矩阵

(三)动态风险溢出网络

为捕捉全球主要股市风险溢出网络的演化特征，图4展示了样本期间风险溢出网络拓扑特征的变化情况。总体而言，平均路径长度与聚类系数保持反向变动关系，且聚类系数较高，平均路径长度较低，表明风险溢出网络可能具有的“小世界现象”。具体可分为以下四个阶段。第一个阶段为2000年至2005年10月左右，自2000年美国股市大崩盘以来，全球股市一度处于低迷状态，复杂网络的聚类系数整体呈缓慢上升的态势，平均路径长度下降。第二阶段是2005年10月至2008年初，随着美联储降息调整，逐渐恢复发展，以及中国2005年的股权分置改革，股市迎来了春天。金融市场风险溢出局面缓和，复杂网络的聚类系数急剧下降，平均路径长度增加。第三阶段是2008年金融危机期间，这一时期复杂网络的聚类系数大幅变动，甚至达到峰值，表明随着全球金融危机的爆发，股票市场风险传染的幅度加强，节点之间联系更加密切。由于危机期间股市脆弱，金融市场悲观情绪弥漫，一国股票市场受到冲击很可能通过贸易渠道、流动性不足、共同贷款人等渠道传染其他国家的宏观经济的基本面，造成大面积的恐慌。这种影响一直持续到2011年危机之后的休养生息阶段，全球股市发展相对稳定，各国风险传染的程度减弱。第四阶段为2013年至2018年，这一阶段波动频繁，整体具有缓慢下降的态势。期间聚类系数在2013年和2015年中期波动剧烈，在2015年波动更为频繁，可见美联储加息和原油价格暴跌等重大事件的发生对全球股市造成了一定的冲击，中国股灾也在一定程度上加强了股票市场的风险传染。经济金融等极端事件的发生加剧了全球股市间的风险溢出，风险溢出网络更加紧密，经济金融稳定时期的风险网络相对松散。

为考察风险溢出网络是否具有“小世界”特征，随机生成1 000个与整体网络等规模的随机网络，计算其聚类系数与平均路径长度(结果见表7)，并与时变风险溢出网络的结构特征进行对比，发现时变风险溢出网络的平均路径长度略低于随机网络，聚类系数均高于随机网络，时变风险溢出网络具有小世界性，这与刘海云等的研究结论一致[13]。

图4 股票市场风险溢出网络结构特征变化的时序图

表7 网络的结构特征

限于篇幅，无法将4 937个动态风险溢出网络一一展示，仅选取6个时点的网络作为代表。图5中前五个图为危机期间的风险传染网络，分别是2000年4月14日、2008年10月7日、2015年8月25日、2016年1月1日以及2016年6月23日的网络拓扑图(3)2000年4月14日、2008年10月7日、2015年8月25日、2016年1月1日以及2016年6月23日分别对应美国股灾、次贷危机、美联储加息和石油价格暴跌、中国A股实行熔断机制、英国脱欧的时间。，最后一个为随机选取的非危机时点的网络。总体而言，前五个网络的节点联系紧密，没有任何孤立的点，表明危机期间全球主要股市的风险溢出较强。EMEA样本最多，风险溢出关系最为明显。虽然美洲大陆样本最少，但其风险溢出数量大于亚洲地区，尤其是美国，多次靠近中心位置，这种情况在2008年10月7日的网络中更为明显。另外，前五个网络的密度、节点平均度、集聚系数均显著较高，揭示了危机期间各国风险传染的密切与复杂关系。其中，2008年10月7日的指标最大，说明此次金融危机的爆发在全球股票市场上的传染面广、传染深度大。作为对照随机抽取的2007年3月12日非危机时点的网络，网络密度均小于危机期间的密度，但依然大于0.5，说明在经济平稳、金融安全的时期也应该进行风险的预警与防控。

四、结论与建议

本文基于时变Dcc-Garch-Copula-ΔCoVaR模型测度2000年1月3日至2018 年12月4日全球30个主要股票市场的时变风险溢出，构建静态与动态风险溢出网络。从静态角度剖析股票市场风险传染网络的结构与特点，分析节点的中心性以及板块特征，识别风险传染的源头以及各个国家在风险中扮演的角色和起到的作用；从动态角度分析样本期间风险溢出网络的时变特征演化趋势。全球主要股票市场间的时变风险溢出的集聚与波动变化不尽相同，主要结论如下(4)关于30个股票市场的风险溢出，笔者也分别采用美国道琼斯指数以及深证成指替换纳斯达克指数以及上证综指进行稳健性检验，经过分析，指标的变化基本没有改变关于风险溢出网络特征的三条主要结论，本文基于30个股票市场的主要研究结论是稳健和可靠的。为了节省篇幅，这里没有报告所有的检验结果，感兴趣的读者可以向作者索取。：

其一，时变Garch-Copula-ΔCoVaR模型测度美国、日本、英国股市对中国股市的时变风险溢出为负。中国内地股市受英国股市的风险溢出最大。港股受到美国以及英国的时变风险溢出更为直接和明显。

其二，静态全局网络下的中心性和“块模型”分析表明美、英等国是风险溢出的中心，中国是风险传染的中介渠道，欧洲国家的风险溢出具有明显的非对称性。各国风险的板块聚类特征明显，主溢出板块的成员地理分布广泛，多为金融发达的国家和地区，如美国、英国、日本等；经纪人板块成员均为亚洲国家；主受益板块成员多为欧洲国家和一些发展中国家，如希腊和土耳其。

图5 局部风险溢出网络图注：圆上数字标注了各层节点度的大小，各地区股票市场根据自身节点度的大小从内到外排序。

表8 风险溢出网络的特征

其三，动态风险溢出网络符合小世界特征。聚类系数与平均路径长度基本呈反向变动，在危机期间急剧增加，危机之后普遍减弱。危机时点比非危机时点的网络密度大、连接渠道多、风险溢出强。

依据前述结论，本文得到如下政策启示：第一，各国应密切合作加强跨国市场的审慎监管，并尝试建立全球统一的风险防范与监管准则。全球主要股票市场之间风险溢出的负向性与网络化致使风险传染范围广、传播速度快，在经济全球化、资本市场不断开放的今天，一国很难在危机中独善其身，因此应该集合众人之力实施监管，制定统一的国际监管准则以及风险隔离机制。第二，发挥“主溢出”作用的发达国家应加强自身股票市场的监测、预警与防范，从源头上防范和化解风险。将大数据以及人工智能等先进技术引入到股票市场风险监测中，加大股票市场监测力度并捕捉日常交易中可能存在的异常信号，降低风险传染到“主受益”国家的可能。第三，鉴于中国极易成为风险传染的中介渠道，更容易暴露在风险环境中，金融业在寻求开放突破的同时要兼顾开放的力度，提高金融业的竞争力主动化解风险。第四，跨国投资者在制定投资组合策略时应从全局出发，充分考虑各国金融市场的风险溢出关系，合理评估风险，及时调整投资策略。