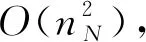大样本数据中方差变点的两阶段估计方法

张 笛,赵文芝,杨银倩

(西安工程大学 理学院,陕西 西安 710048)

0 引 言

变点问题一直都是统计学的研究热点。在某个未知时刻,样本的分布发生了突然的变化,这个时刻就称作变点。 1954年，Page发表的一篇质量检验的文章提出了变点问题[1],引起了众多学者对变点问题的关注,现在变点研究已被大量应用于金融经济学、医学诊断等领域。

在经济金融中,常用方差度量风险,关于方差变点的文献也有很多。 Gombay等对独立序列中的方差变点进行检验和估计,得到了变点估计量的渐近性质[2]； 邵钏利用滑窗法证明了独立序列中变点估计量的弱、强收敛速度[3]。 以上文献都是考虑独立情形,实际中的数据通常具有相依性。 赵文芝等应用CUSUM估计量,在较弱条件时推导出线性过程中估计量的收敛速度[4]。 由于CUSUM检验需要估计模型参数,孙耀东等在非参数回归模型中,构造Ratio 检验统计量并研究了其极限性质[5]。在消除序列相依性的同时,金浩等通过Bootstrap方法提高了自回归模型中方差变点的经验势函数值[6]。 由于变点所处位置对其检测效果有一定影响,在独立正态随机变量序列中,Hsu在初始方差水平未知时对方差变点进行2种检验[7],王静龙等在均值未知时构造了方差变点的3种检验统计量,通过模拟得出变点所处不同位置时对应的最优检验统计量[8]。 此外,秦瑞兵等提出一种截断样本的方法，使估计精度得以提高[9]。

在统计检验实践中,常常会发生均值和方差变点同时存在或更复杂情况。Pitarakis发现均值和方差变点相互作用,因二者之一在最小二乘估计中被忽视而出现推断错误情况[10]；Bai用拟极大似然方法对面板数据中均值和方差公共变点进行估计,得到了方差变点的相合性和渐近分布[11]；胡尧等对于双重变点采用小波方法, 得到方差变点跃度的估计[12]；王慧敏等研究了相依序列中均值和方差变点同时存在的CUSUM 估计量[13]；陈璐等进一步研究了均值已知和未知时相合性和收敛速度的影响[14]。 当变点个数不止一个时,Inclan等应用CUSUM 型估计量检验独立序列中多个方差变点问题[15]。 相对于突变点,渐变点更能刻画现实数据特点,刘鑫等利用最小二乘方法研究了面板数据中方差渐变点的估计问题[16]。

随着经济飞速发展,统计产出数据呈指数型递增,快速估计方差变点可使得人们及时调整思路以减少损失。本文针对大样本数据提出了快速估计变点的两阶段估计方法,证明了估计量的相合性和收敛速度。

1 统计模型及假设

考虑如下方差变点模型:

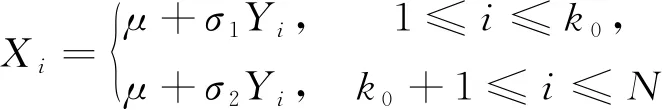
(1)

式中：μ为常数；σ1≠σ2为常数，即σi取值考虑简单情形；k0为未知变点。Yi是给定的线性过程，

式中：V(·)、E(·)分别表示对随机变量取方差、均值运算。

对模型(1)进行移项,得Xi-μ=σiYi,故

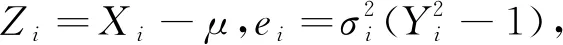
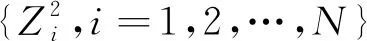
k0的最小二乘估计量为

(2)

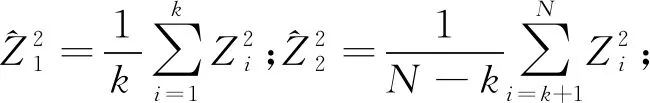
i=k*+(t-1)·dN

(3)

2 变点的两阶段估计

2.1 初始估计量

引理1若假设1和假设2成立,可推得γ=η。

(4)

(5)

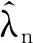
(6)

2.2 最终估计量

由子序列与原序列的下标关系式(3)及式(6)可得,P(k0∈[h1,h2])→1成立,其中

第二阶段对原序列中落入随机区间[h1,h2]的所有样本进行估计,估计方法如下:

(7)

3 定理及证明

(8)

式中：P(k0∉[h1,h2])<ε,ε为任意小的正数。

|E(Uk0)|-|E(Uk)|≥Gη|λN(ρ-η)|

(9)

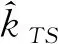
(10)

(11)

经过简单计算可得

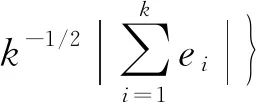
(12)

再由文献[4]的定理1和定理2可得

从而，

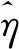
(13)

定义

DN,S={k:Nδ≤k≤N(1-δ),k∈[h1,h2],

则

(14)

由于

0≤f(k)≤1

(15)

假设λN>0,由E(Uk0)>0,得,

(16)

因为E(Uk0)={η(1-η)}1/2λN,由Hjek-Rényi不等式[19]知,当N→∞时，式(16)中前两项均趋于0,所以P1→0。

对于P2,由Uk-Uk0≥0可推出

Uk-E(Uk)-(Uk0-E(Uk0))≥

E(Uk0)-E(Uk)

(17)

由式(9)和式(17),得

A(k)+R(k)≥E(Uk0)-E(Uk)≥

则

(18)

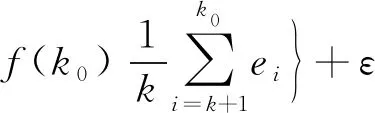
(19)

由式(15)和k≥Nδ,有

(20)

(21)

其中C1>0。当N,S→∞时,式(21)中的3项均趋于0，则P2,2→0。 同理,P2,1→0，则式(14)趋于0。

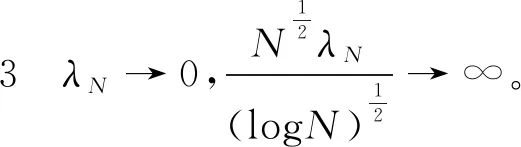
定理3在假设1～3成立条件下,

证明在下面证明中,U(k)和Uk是等价的可互换。由定理2可知

(22)

且

∀Q>0,有|v|≤Q,定义[-Q,Q]上有统一度量标准的连续函数空间C[-Q,Q]。记

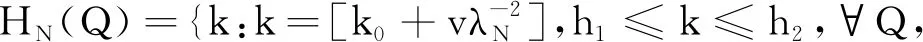
则

2N(Uk0-E(Uk0))(Uk-Uk0)+

N(Uk-Uk0)2

(23)

首先证明在集合HN(Q)上,式(23)的后两项是趋于0的。由式(12)可得N1/2(Uk0-E(Uk0))是有界的,仅需证明N1/2(Uk-Uk0)在HN(Q)上是趋于0的。

N1/2|Uk-Uk0|≤N1/2|A(k)+R(k)|+

N1/2|E(Uk)-E(Uk0)|

(24)

易知关于R(k)的上界依然有效,对式(20)乘以N1/2,由不变性原理,经过计算均依概率趋于0。同理,在集合HN(Q)上N1/2A(k)→0。对于式(24)第二项,易知∃V>0，使得V(N1/2λN)-1→0。由式(15)和k∈HN(Q),得

0≤N1/2(E(Uk0)-E(Uk))≤

N1/2(f(k0)-f(k))λN+

V(N1/2λN)-1

下面证明对于k∈HN(Q),

(25)

NλN(Uk-Uk0)=NλN(A(k)+R(k))-

NλN(E(Uk0)-E(Uk))

(26)

式中：“⟹”为弱收敛；W1(·)为[0,∞]上的布朗运动。由于

因此

NλN(A(k)+R(k))⟹{η(1-η)}-1/2·

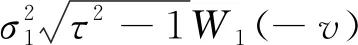
(27)

NλN(E(Uk0)-E(Uk))=

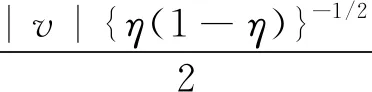
(28)

结合式(25)～(28),当v≤0时,有

同理,当v>0时,有

的极限分布。因为W1(·)是由i≤k0时的{ei}决定的,同样W2(·)是由i>k0时的{ei}决定的,所以W1和W2由不相重叠的序列{ei}决定且彼此独立。

为了证明定理3,定义Cmax[-Q,Q]是C[-Q,Q]上函数存在唯一最大值时的子集,且argmax函数在Cmax[-Q,Q]上是连续的,利用连续映射定理,可得

4 随机模拟

由模型(1)产生随机数据,即

其中Yi是AR(1)过程,Yi=φYi-1+εi,φ=0.3,εi为服从N(0,1)的独立同分布序列。取N=4 000、6 000、8 000,k0=0.5N,k*=0.5dN,BnN=lgnN,lnnN,log2nN,每次估计重复1 000次,结果如表1所示。其中,Mean,Std和Toc分别表示模拟1 000次时的估计值、标准误差和运行时间。T-S估计表示所提出的两阶段估计方法,L-S估计表示传统的最小二乘方法。

表 1 2种方法模拟1 000次的对比

由表1可知,随着样本量N的增大,估计所需运行时间越来越长。当样本量N一定时,随着BnN的增大, 所提方法的最终估计值不断靠近传统方法的估计值,标准误在不断减少; 运行时间有所增加但优于传统方法的运行时间,估计效果不断提高。 尤其当BnN=log2nN时,两阶段估计法的估计值最为接近传统方法的估计值,且时间相比传统方法的估计时间缩小一半甚至更少。数据量N越大估计结果愈加准确,体现了大样本数据中二阶段估计方法的有效性。

5 结 语