手写液晶体数字及识别技术

丁 娜，钟宝江

苏州大学 计算机科学与技术学院，江苏 苏州 215000

1 引言

字符识别是模式识别的一个研究热点，手写数字识别技术作为其重要的研究分支，得到了广泛的关注与发展。手写数字识别是一种利用计算机以及一些识别设备自动辨认手写阿拉伯数字的技术。常见应用主要包括邮件自动分拣、财务报表、银行单据的检查和处理、数据录入等。这些任务一般都需要非常高的识别精确度和非常快的识别速度。然而，不同人的手写风格迥异，差距较大，因此手写体数字的格式难以规范，准确识别有较大的难度。为此，本文设计了一种利用“液晶体”记录数字的方式，并进一步提出了一种对应的快速识别方法。与普通的手写体数字相比，手写液晶体数字在格式上比较规范统一，从而可以通过低复杂度的算法完成高精度的识别。

手写液晶体数字识别的关键问题在于：不同样本在笔画深浅和笔画粗细上存在差异，并且冗余笔画会形成噪声，影响识别效果。传统的字符识别方法会对输入图像先进行一系列预处理操作（如高斯模糊化、二值化、形态学运算等），再进行特征提取，旨在减少这些差异与噪声带来的识别错误。这些预处理步骤往往使得算法过程复杂化，并且可能出现不稳定的识别结果。为此，本文提出的识别技术将直接对输入的待识别数字图像进行特征提取，能够尽可能完整地保持原始的图像信息，同时保证算法运行的稳定性。该技术将不同人的书写风格归一化，使得输入的待识别样本转化为一个基本不变的数字表示。最后，实现了对手写液晶体数字的可靠分类和识别。与现有方法相比，新方法的识别过程简单稳定，却能够取得更好的识别效果。

本文以计算机阅卷系统的研发为背景，在这一任务中，对学生学号的识别需要有尽可能高的准确率。比如一个学号由10 位数字组成，则需要10 位数字都能正确识别，该学号记录才能有效。也就是说，在这一应用场景中对单个数字识别的损失函数是通常识别任务的10倍。目前主流的数字识别方法是神经网络算法[1-7]。在本地区中小学校采集了一批通常的手写体数字样本，运用在标准的手写体数据库，即MNIST 数据库（http：//yann.lecun.com/exdb/mnist/）上训练出的神经网络模型对其进行识别，正确率仅有62%左右，效果很不理想。如果期望提高正确率，则需要扩大或者更换训练数据集，重新训练网络模型，工作流程复杂，且对于专业知识和硬件设施的要求也比较高。即便如此，对单个字符的识别率一般也只能提升到99%左右。此时对于一串包含10位数字的学号来说，其识别的准确率仅有90%，依然不够理想。在其他类似的应用场景中，数字一般也都是以字符串形式出现的。可见，单个手写体数字的识别准确率需要进一步提升。

本文提出的液晶体数字记录方式将解决问题的关键步骤前置，采集到的待识别数字样本具有相对规范的格式，从而能够显著减轻后期识别阶段的压力。对应提出的识别方法基于贝叶斯分类器来实现，无需事先训练，算法复杂度低，在排除用户未按照要求的模板书写的情形后能够实现100%的识别率。与现有方法相比，其优势非常明显。

2 相关技术

在计算机视觉和文本图像分析领域，手写数字的识别技术已经取得了巨大的进展。1998 年，Kundu 等人[8]利用可变持续时间隐马尔可夫模型和路径判别隐马尔可夫模型策略，实现了一种手写文字识别系统。2007年，Wen 等人[9]提出了一种手写孟加拉数字识别系统，在邮政信件自动分拣机上得到了实际应用。该系统主要采用了支持向量机分类器，并且结合主成分分析特征提取器，能够快速地给出识别结果。此外，研究人员已经对隐马尔可夫模型[10]、支持向量机、Fisher 线性分类器、随机森林、k-近邻[11]等多种分类器模型进行了研究。这些传统的分类模型在小规模数据集上可以达到较好的识别效果，然而在大规模数据集上的识别率和收敛速度都不够高。总体来说，基于传统的手写体数字识别算法简单，速度快，但是并不能达到百分百的精度需求[12-13]。

近年来，深度学习技术的发展为解决手写体数字识别提供了新途径。一批基于神经网络的识别方法被提出[1-7]。作为一种新的机器学习方式，深度学习吸引了人们的广泛关注。深度学习基于一组算法，试图通过使用多个非线性信息处理阶段对数据建模进行更高层次的抽象，重点学习数据的表达[14]。在深度学习环境中，基于表示学习的模式识别任务已经成功实现[15]。由于数据的可用性和对分类任务的高准确性和良好泛化能力，神经网络已经成为解决问题的主要方法。卷积神经网络（Convolutional Neural Network，CNN）在字符和数字识别上展示了优秀的识别率[16]。CNN 技术的优势在于能够自动提取输入字符中不变的显著特征[17-18]。虽然这些模型具有较高的精度，但是为了实现对神经网络的权值进行微调以便提取出更好的特征，并使收敛速度慢于最优解，需要付出相应的代价，即大量的计算和复杂的体系结构开发。对于手写体数字的识别，目前大都基于MNIST 手写体数据集进行训练识别。图1 展示了该数据库中两批不同的样本，可以看到在书写方向、数字大小、笔画粗细深浅等方面这些样本存在明显不同的风格化特征。如前所述，若使用MNIST 数据库上训练出的模型来对该数据库以外的手写体数字样本进行测试，识别率很低。也就是说，基于特定数据集进行训练的神经网络模型，对非数据库中的样本进行识别时准确率并不理想。因此，目前在实际应用中，CNN神经网络识别算法不够稳定，其泛化性能的提高是一个瓶颈性的难点，并且使用成本非常高。

图1 不同风格的手写体数字样本

为了保证识别的超高精度，一般会考虑使用答题卡系统。答题卡上的信息通过光标阅读机识别，用配套软件使涂点数据录入到计算机中，如图2（a）所示。然而，答题卡系统的设备成本高，且使用不方便，灵活程度低，限制了其应用范围。一方面，光标阅读机对信息卡的定位精度要求较高，因此制作一张答题卡有很多要求，比如纸张纤维要长、薄厚均匀、挺括程度好等，并且在印刷的套印和基准边的裁切精度方面也要求很高，否则很容易造成阅读错误，降低识别精度。此外，因为答题卡纸张纤维具有很强的亲水性，在温度急剧变化时涨缩也较大，所以机读答题卡的存放与保管也需格外小心。另一方面，在答题卡填涂方面也非常讲究，必须时刻保持答题卡的页面整洁、不得折叠，需要使用指定的2B铅笔进行特定形状的填涂，否则会无法识别。在设备成本方面，市场上光标阅读机的价格为1 万元左右，外设条件要求更高。因此，答题卡系统大多用于一些重要的考试场合，实际应用范围小。相对地，本文提出的计算机阅卷系统不仅在设备成本、使用方式等方面具有明显的优势，同时也契合当前互联网以及个人液晶图像设备（如手机）十分普及的时代特点，能够在大范围内灵活与广泛地应用。

本文所设计的手写液晶体数字的结构简单，可以使得不同人的书写风格尽量保持一致，如图2（b）所示。进一步地，将基于贝叶斯分类器来设计一种无需事先训练的识别算法。贝叶斯分类器通过计算样本的最大后验概率进行分类，适合处理多分类问题，并且在小规模数据集上的处理效果很好。同时，虽然该算法的程序实现简单，运行速度快，但是却能达到理想的识别精度。

图2 两种答题卡学号识别区域的对比

3 手写液晶体数字

3.1 手写液晶体的提出

数字是一种用来表示数的书写符号，国际通用的数字是阿拉伯数字。不同人的书写风格不同，因此手写体数字从形态、大小、结构、深浅等各方面都会存在明显差异，部分手写数字甚至难以被人眼识别。如前所述，对于计算机阅卷系统这类场景来说，对单个数字的识别准确率要求非常高，传统手写阿拉伯数字的多变性将使得解决这一问题变得异常困难。答题卡识别系统虽然识别率高，但由于涂写结果并不直观、难以检查等因素，涂错数字的情况也时有发生，而且使用成本过高，因此无法普及。受数码管上液晶字体（如图3（a）所示）的启发，本文提出了一种新的手写体数字记录方式，即“手写液晶体数字”。在设计液晶体数字的模板（如图3（b）所示）时，考虑到大部分人的书写习惯，将该模板整体设计成略向右上角倾斜。为了保证用户能够正确书写，同时会给出标准的数字样例，如图3（c）所示。基于这一数字记录方式，后期的识别正确率能够得到有效保证，从而很好地解决前面两类识别系统遇到的问题。

相比通常的手写数字样本（见图1），本文所采集到的手写液晶体数字样本（如图3（d）和（e）所示）的结构稳定，风格相对统一，从而保证了识别的正确率。与传统答题卡系统相比，使用者能够直观地检查自己的书写结果，避免传统答题卡上容易出现的填涂错误。另外，一般的扫描机或者手机拍照后的图像都可以在系统中直接进行处理和识别，不需要特殊的阅读机，也不需要额外特殊的答题纸与答题笔，显著提升了系统使用的便利性。

图3 液晶数字及手写数码体学号

3.2 液晶体数字数据库

从本地区中小学校中采集了6 386个手写液晶体数字样本，建立了一个用于测试的数据集，其中包含10种数字类别，即0～9这10类数字。图4展示了10种数字类的部分样本。书写的工具包括铅笔（着色淡，见图3（d））和黑色签字笔（着色深，见图3（e）），并且因为不同学生在笔画深浅、粗细、连贯性等各方面有所差别，使得数据集中的样本具备多样性与真实性，保证了实验的合理性、测试的准确性以及本文方法的有效性。

图4 本文提出的数据集的部分样本图

此外，为了模拟真实的应用场景，数据集中包含了少量未按规则填写的数据样本和漏写的空样本。为此，本文的识别算法将增加“拒判”这一分类结果，并将通过人眼验证的合理“拒判”当作正确识别结果。图5 给出了两个被“拒判”的样本，这些样本均没有按照模板要求的格式进行书写，因此“拒判”为正确的识别结果。

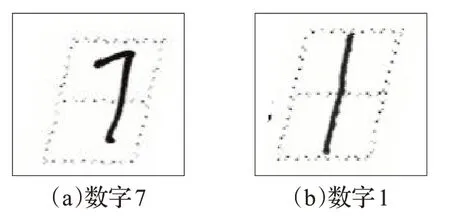
图5 被合理“拒判”的样本

4 识别算法

为了保证识别过程和结果的稳定性，本文没有采用传统识别方法中对图像样本进行的预处理操作（如图像模糊化和二值化）。这类预处理步骤主要是为了提高算法对于图像噪声的鲁棒性，但同时也会丢失图像的部分有效信息，使得识别结果变得不稳定。本文的识别算法将直接从原始样本的图像中提取特征，过程稳定且计算复杂度低，同时通过贝叶斯模型的特点（即基于后验概率进行分类）来保证算法的抗噪性能。图6给出了本文识别算法的主要步骤。具体地，首先基于液晶体数字模板的坐标设置7 个窗口，由此采集数字图像的信息特征；然后依据贝叶斯判决方法将待识别样本的特征与10类不同数字的标准特征向量进行匹配；最后根据最大后验概率准则完成分类和识别。该算法的计算复杂度低，因此具有很快的识别速度，满足在线实时识别的要求。

图6 基于贝叶斯分类器的手写数码体数字主要步骤

4.1 特征提取

手写液晶体数字样本一共包含10 个类别，分别由ω0,ω1,…,ω9表示。其中ω0表示数字0的类别，ω1代表数字1的类别，以此类推。此外测试数据集中包含了部分实际无效（即没有按照要求书写，需要被合理“拒判”）的样本。

本文识别算法直接对输入的待识别液晶体数字图像进行特征提取。液晶体数字的模板在7 个位置记录不同数字的笔画。根据这一结构，可在这些位置上相应地设置窗口来采样可能出现的笔画，如图7（a）所示。

本文分别用R1,R2,…,R7表示这些信息采样窗口，基于采样结果，每个待识别数字都会被表示为一个7维向量。由于横向的笔画和竖向的笔画有不同的长度，采用了两种不同尺寸的窗口分别覆盖（见图7（a））。如果窗口尺寸过小，则可能会将采样到的噪音点当作真实笔画，形成笔画存在的假象，从而导致错误识别。为此，选择较大尺寸的窗口，保证了笔画采样的可靠性。

由于书写误差的问题，在初始设定的位置上这些窗口可能不仅覆盖了目标笔画，还包括了相邻窗口对应笔画的一部分，这时目标笔画会被错误表示。为了解决这一问题，允许窗口的位置在一定范围内浮动，得到多个采样结果，最终依据灰度值之和最大（包含黑色像素点最少）的窗口来判断笔画是否存在。如果这一灰度值之和小于给定的阈值，则认为在对应的位置上出现了笔画，称之为“有效笔画”。图7（b）和（c）分别列举了对于数字“3”和“4”的识别过程。对于数字“3”，有5 个窗口被确认为存在有效笔画；而对于数字“4”，只有4个窗口出现了有效笔画。为了表示待识别的数字样本，记：

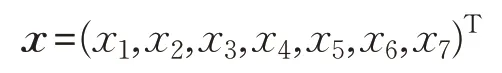
其中，xj(j=1,2,…,7)表示待识别图像中液晶体数字的7个笔画窗口内的灰度值之和。由于不同数字样本在笔迹的粗细、深浅方面均有差异，而且同一个样本的横向笔画和竖向笔画粗细也可能都不同，为了得到不变的样本表示，以横、竖两个方向上的有效窗口灰度值的均值分别对两个方向上笔画的特征值进行约化。为了便于表示，约化后该样本的特征向量仍然用向量x表示。

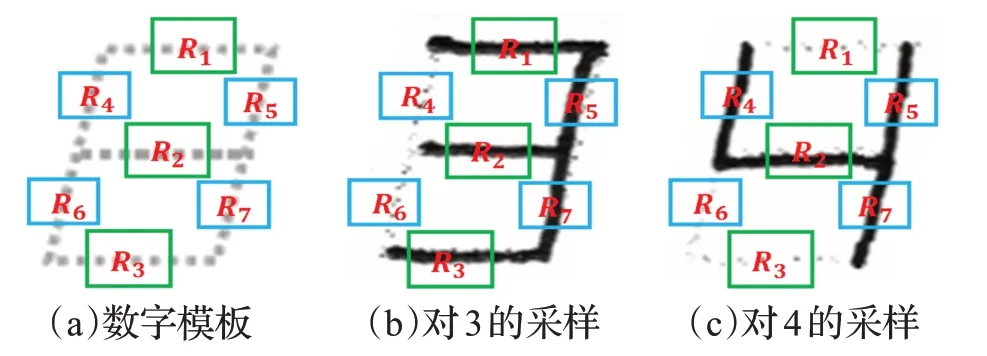
图7 采样窗口的配置

用ri分别表示0～9这10个数字类的标准特征向量：

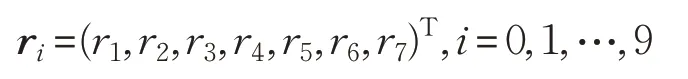
具体来说，向量ri中某个元素值若为1，则表示模板的对应位置有笔画存在；若值为0，则表示对应位置无笔画。例如，用向量r2=(1,1,1,0,1,1,0)T作为ω2（即数字“2”）的类特征表示，可解释为第四和第七分量所对应的位置无笔画，其余位置均有笔画。表1列出了所有数字类的特征向量。

4.2 分类识别

贝叶斯分类器是一种基于贝叶斯定理和最大后验概率确定新样本输出属性的概率分类模型[19]。基于输入特征相互独立这一假设来计算概率，实现对模型的分类，适合处理多分类问题。因此，本文选择了该分类器来识别液晶体数字，虽然算法结构和实现简单，但在识别速度和准确率方面均达到了理想的效果。

首先，对于每一个数字类别ωi，计算其先验概率，计算如下：

表1 10个数字的类特征向量

其中，Ni表示数据集中第i类数字图像的数量，N表示数据集中数字图像的总数。在学号识别这一应用场景中，10个数字类的先验概率显然均为0.1，这是先验概率相等的情形。其他场景中也可能会出现先验概率不相等的情形，比如在识别身份证号码时，身份证序列的第一位只能取1～6 和8 这七类数字，显然这十类数字的先验概率不是相等的，这七类数字的先验概率将大于其他三类数字。可以依据统计数据分别配置10个数字类的先验概率，从而保证最终识别的准确率。

接着，基于待识别的数字样本和每一个数字类的特征向量之间的距离来计算其属于每一类数字的似然性pi，计算如下：

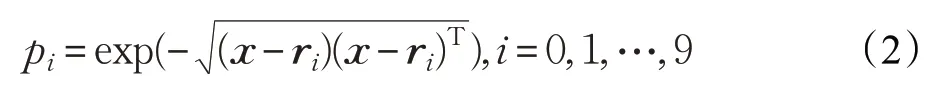
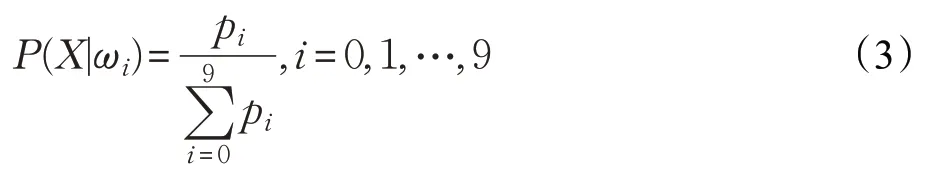
最后，根据贝叶斯公式计算待识别样本的后验概率分布，计算如下：

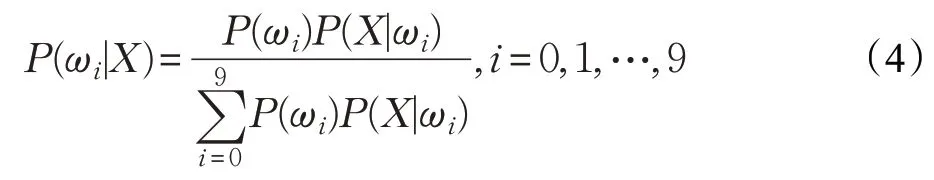
根据贝叶斯分类准则，后验概率取值最大的类即为待识别样本所属的数字类别，即：

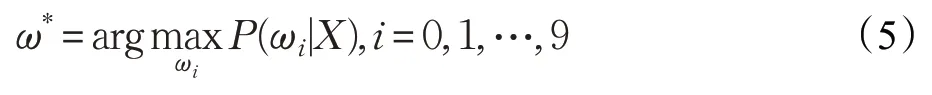
如果用户未按照规范进行书写，则会导致分类结果不可靠。为了区分这种情况，可以考虑含“拒判”决策的分类方法，即如果

则对X拒判。结合式（5）和（6），本文具体的分类模型表示为：

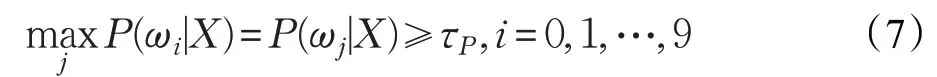
其中，τP默认值为0.16。

图8 给出了数字“5”的三个手写液晶体数字样本。图8（a）中的样本笔迹较浅，图8（b）中的样本笔迹较深，图8（c）中的样本没有按照模板书写，从而无法从设置的窗口中正确采样笔画。这三个样本在不同数字类上的后验概率结果如图9所示。容易看到，前两个样本的后验概率具有大致相同的分布规律，并且都在“5”这个数字类上达到最大值，从而被正确识别。

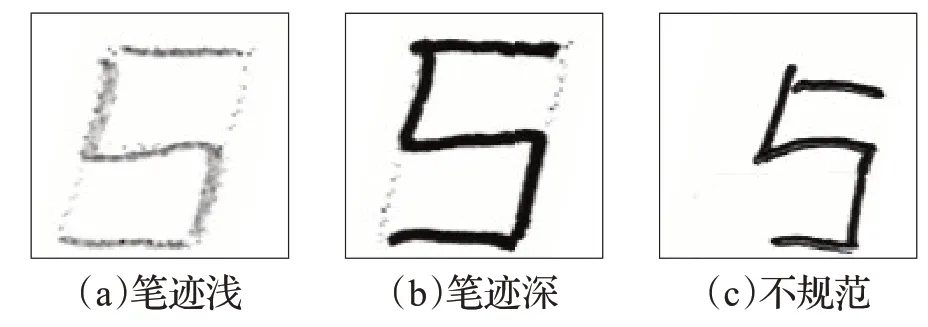
图8 数字“5”的三个样本

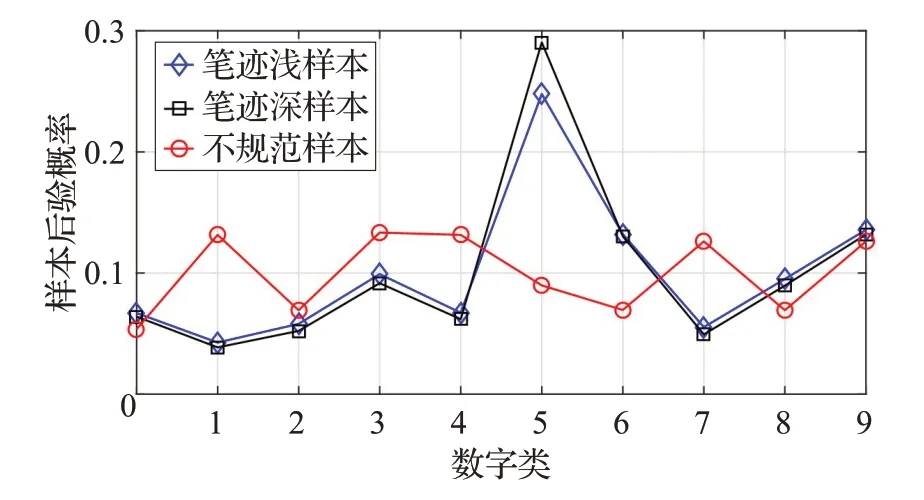
图9 数字“5”的三种不同样本的后验概率

可见，基于后验概率的分类过程对于笔迹深浅具有明显的不变性。而不按照模板要求书写的第三个样本，其最大后验概率小于给定阈值，即属于每一个数字类的概率都很低，因此被合理拒判。

4.3 容错策略

对于计算机阅卷系统来说，考虑到各个用户的书写习惯不同，可能不会完全按照数字模板要求填写，导致实际的手写液晶体数字样本与标准模板数字之间存在差异，形成错误的识别。但这些样本可以被人眼准确识别，那么也应该属于本文算法的正确识别范畴。因此本文设计了一种容错策略来识别这类样本。

基于采集到的数字样例，本文总结出了一些具有代表性的“错误样例”（如图10 所示），大概占样本总数的1.36%。为了正确识别这些人眼可以容忍的错误，在识别系统中加入了以下容错策略，从而提高了识别的效率。

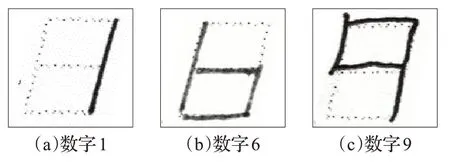
图10 人眼可以容错的书写错误

根据实际采样结果，只有1、6、9这三种数字类别需要进行容错，其容错表示称为“容错码”，如表2 所示。在分类时，对这三类数字的特征向量进行了补充，也就是将待识别样本的特征向量与这三个数字类的标准码及容错码都分别进行概率计算，然后依据概率值高的结果进行分类，得出最终识别结果。

表2 “1”“6”“9”数字类的容错码

若算法中没有增加这个容错策略，则上述三种“错误”的数字样本会被分类错误或者被拒判，识别率并不理想。因此，该容错策略有效地增加了识别算法的可靠性与识别系统的可用性，提高了识别准确率。

5 实验结果及分析

以下通过仿真实验来评估本文方法的有效性。由于手写液晶体数字是本文提出的新的数字记录方式，目前没有其他可使用的同类数据集，无法进行量化结果的直接对比。在手写数字识别领域，近几年来基于神经网络的识别算法取得了显著成效，具有一定的影响力。因此为了进行性能评估，将所提出的方法与目前三种具有代表性的神经网络方法（LeNet[20]、AlexNet[21]和VGG16[22）]进行了比较。采用的评价指标包括识别的正确率、在数字串识别时的损失函数值、识别的抗噪性能以及算法运行时间四方面。

5.1 评价指标

识别正确率是分类效率的一种度量，是比较各种分类方案好坏的主要标准。正确率越高，算法识别效果越好。算法的正确率即用识别正确的样本数除以样本总数得到：

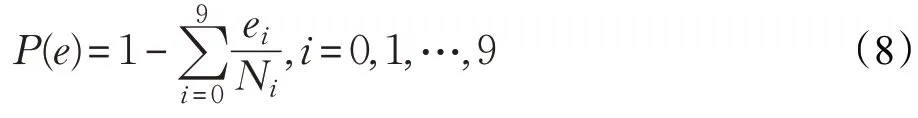
其中，ei表示第ωi类中样本被错判为其他类别的数量，Ni为每一类的总样本数。

由于对数字的识别任务一般会出现在对字符串进行识别的场景中，本文考虑的第二个评价指标即为单个数字识别对整个数字串识别的损失函数值。该损失值反映了所使用的识别方法在识别错误时所产生的风险。计算机阅卷系统中的一组学号由十位数字组成，即需要满足十位数字都能识别正确学号记录才能有效。因此，损失函数计算如下：

其中，ei表示第ωi类中样本被错判为其他类别的数量，λ=10 为损失系数。

本文对测试数据集中的数字样本加上不同强度的高斯噪声与椒盐噪声，通过最终识别率的变化来反映各算法的抗噪性能。

在统计识别时间方面，对于神经网络算法的描述包括了训练时间与测试时间，而本文算法无需预先训练，因此只包含测试时间。方法的识别时间越少，识别效率越高。

5.2 对比算法

本文选择如下三种具有代表性的手写体数字识别方法进行比较。

LeNet-5[20]：由 Lecun 在 1998 年提出，用于手写体数字识别的卷积神经网络方法。绝大多数的美国银行用该方法识别支票上的手写数字，是早期卷积神经网络中最具代表性的技术之一。在LeNet-5 中，包含2 个卷积层、2个池化层和3个全连接层。输入图像的大小为32×32像素。

AlexNet[21]：由Hinton团队提出，在2012年世界权威的ISVRC（计算机视觉竞赛）中得到了第一名，并因此成为图像分类的核心算法模型，为其后CNN 的发展奠定了技术基础。AlexNet由8个学习层组成，包括5个卷积层和3个全连接层。输入图像的大小为227×227×3像素。

VGG16[22]：2014年ISVRC中使用的神经网络模型，并且获得了第一名。VGG16 由16 个学习层组成，包括13 个卷积层和3 个全连接层，是一个深层卷积神经网络。输入图像的大小为224×224像素。

从整个数据集中随机选取了1 452幅图像作为测试集，剩余的4 934 幅图像作为训练集。为了让所对比的三个神经网络有更好的表现，利用现有已经训练好的模型的权值参数作为初始化的参数，结合新的数据重新训练，从而尽可能弥补训练数据比较少，进而影响识别结果的问题。

5.3 测评与分析

表3 给出了本文方法与所对比的三种识别方法在识别正确率和损失值方面的表现。可以看出，对于其他三种神经网络方面的经典算法，本文方法取得了最高的识别率，达到了100%，完全满足识别精度要求很高的情形。基于损失值的对比，新方法比现有方法对于学号的识别具有更明显的优势。

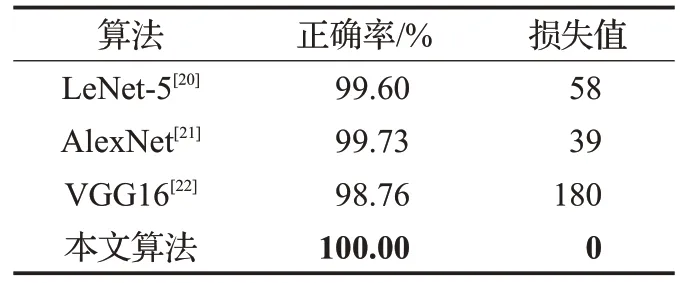
表3 识别结果正确率和损失值

为了测试识别算法的抗噪性能，本文在测试图像上分别添加了不同强度高斯噪声和椒盐噪声。图11和图12分别展示了带有噪声的样本图像。实际环境下，噪声可能会由于拍摄图像的光线过暗或者样本在图像传输或压缩过程中讯号受到干扰而形成。表4和表5分别给出了本文算法与对比算法在高斯噪声与椒盐噪声（方差σ分别为0.1、0.2、0.3、0.4）上的识别率。随着噪声强度的增加，三种对比算法的识别率明显逐渐下降，而本文算法不受噪声的影响，识别率依然稳定在100%，具有优秀的抗噪能力。

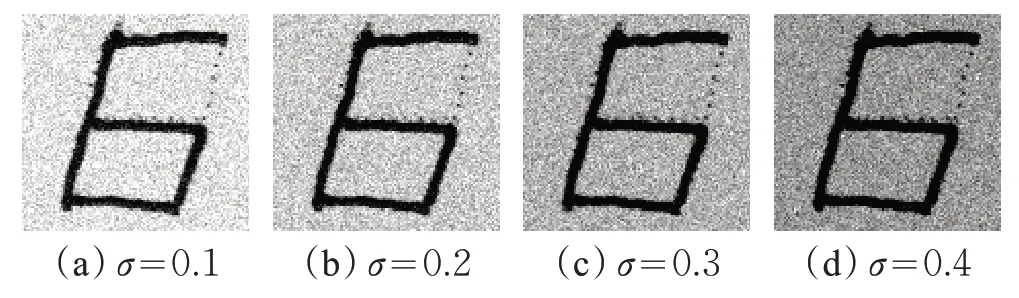
图11 不同强度的高斯噪声样本

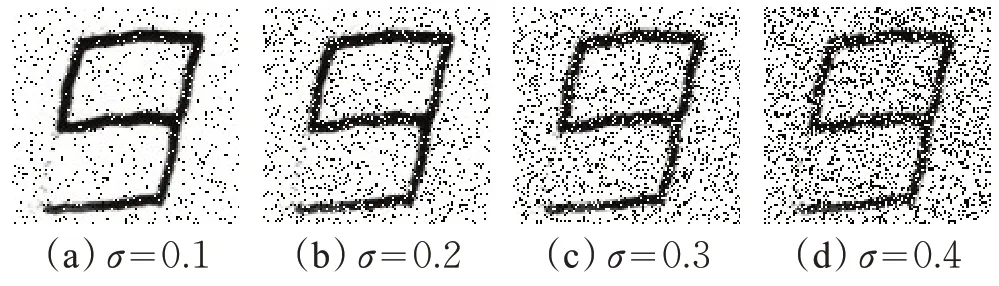
图12 不同强度的椒盐噪声样本

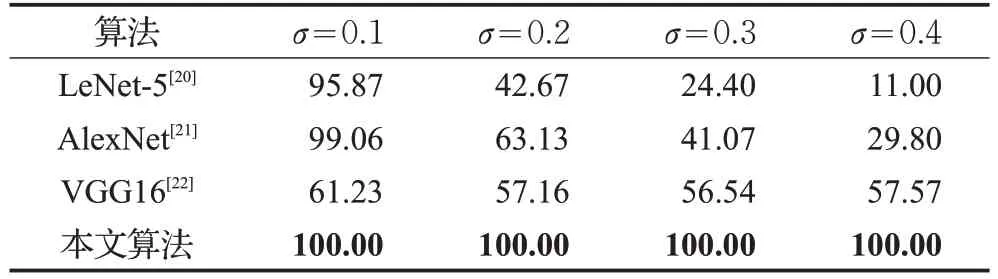
表4 不同强度高斯噪声下各算法的识别率%

表5 不同强度椒盐噪声下各算法的识别率%

5.4 计算复杂度分析

以下用浮点运算次数来分析各算法的时间复杂度。一次浮点运算定义为一次乘法或者一次加法。

卷积神经网络中，n个卷积层的时间复杂度为[23]：

其中，M表示每个卷积核输出特征图的边长；K表示每个卷积核的边长；n表示神经网络的卷积层数，即网络的深度；Cl表示神经网络第l个卷积层的输出通道数。卷积层越多，运算次数越多，时间复杂度越高。由5.2 节可知，在上述三种对比算法中，LeNet-5 的时间复杂度最低，VGG16 的时间复杂度最高。因此只需比较LeNet-5与本文算法之间的时间复杂度。

输入一张p×q的图像，则n=p×q表示所有像素点的个数。将图像缩放为指定尺寸需要遍历所有的像素点，时间复杂度为O(n)。基于式（10）是对运行次数的估算，进而通过估算其运行次数来对比两个算法之间的时间复杂度。在LeNet-5 算法中，卷积核大小为5×5，第一层卷积核的输入通道为1，输出6 张28×28 的特征图，则运算次数约为282×52×1×6；第二层卷积核的输入为第一层的输出，输出为16张10×10 的特征图，则运算次数约为 102×52×6×16 ；因此LeNet-5 总的运算次数约为357 600，而AlexNet 和VGG16 的运算次数则远大于该值。

在本文算法中，首先分别遍历7个窗口中的像素点进行特征提取，其运算次数为600×3+450×4。然后基于贝叶斯分类器进行分类识别。先验概率的计算取决于类别数，则运算次数约为10；类概率密度的运算次数约为330；最大后验概率的运行次数约为31。最后相加可知，本文算法总的运行次数约为4 001，明显低于LeNet-5 的运算次数。由此可见，本文算法的时间复杂度显然低于对比算法的时间复杂度。

表6 给出了不同方法对每个样本的实际平均训练时间和识别时间。所有实验均在以Linux为操作系统的NVIDIA TITAN Xp 的服务器上编译运行。本文算法的明显优势在于其不需要预先训练的时间，却也能达到实时识别的效果，因此效率更高。

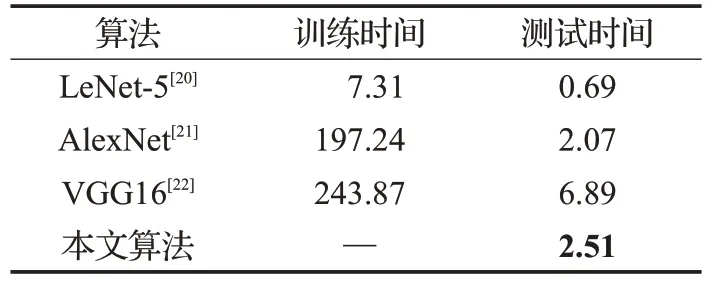
表6 不同算法的运行时间 ms

总体来说，本文算法基于液晶体数字的结构提取特征与分类识别，无需训练步骤，从而其运行不依赖于数据集的大小，但能够取得优于三种神经网络方法的识别准确率、抗噪性以及识别速度。

6 总结

对于需要识别整个数字字符串的场景，对单个数字的识别精度需求很高。为此，本文提出了一种新的手写体数字记录方式，即液晶体数字，并提出了一种稳定可靠、快速有效的识别方法。本文方法首先基于液晶体模板的布局设置了7个图样采样窗口，提取数字的特征信息，并将其转换为样本的特征向量。然后计算样本与各数字类之间的距离，从而基于贝叶斯分类器实现分类。实验结果表明，本文算法能够取得优于现有识别算法的准确率，在算法复杂度、识别时间与抗噪性能方面也有明显优势。