低秩稀疏分解及其在视频和图像处理中的应用

杨永鹏，杨真真，李建林，乐 俊

1.南京信息职业技术学院 网络与通信学院，南京 210023

2.南京邮电大学 通信与网络技术国家工程研究中心，南京 210023

1 引言

低秩稀疏分解（Low Rank and Sparse Decomposition，LRSD）[1-3]是一种将已知数据矩阵分解为低秩成分和稀疏成分的技术，目前被广泛应用于视频的前景和背景分离、图像去噪等方向。该技术是在主成分分析（Principal Components Analysis，PCA）[4-5]的基础上发展起来的。PCA 在数据降维等方面[6]有着显著的优势，但是由于PCA往往会丢失数据的某些特征，导致对损坏较严重的数据处理时存在较大的局限性。在过去相当长的一段时间内，人们为了增强PCA的鲁棒性，提出了很多改进算法[7-8]，但这些算法仍然存在着许多问题，例如，在多项式时间内不能有效求解和不能有效处理恶劣环境下的数据矩阵等问题。近年来，为了进一步改进PCA 算法的鲁棒性，LRSD 算法被提出并引起了人们的广泛关注，成为计算机视觉等领域研究的热点。LRSD算法能够在数据矩阵严重损坏的情况下，鲁棒地恢复出低秩成分和稀疏成分，故又称为鲁棒主成分分析（Robust Principal Component Analysis，RPCA）[9-11]。传统的LRSD模型如下所示：

其中，M∈ℝm×n为待处理的数据矩阵，L∈ℝm×n为低秩矩阵，S∈ℝm×n为稀疏矩阵，rank(L)表示低秩矩阵L的秩函数为稀疏矩阵S的l0范数，表示矩阵S的稀疏度，λ为折中参数。该模型是非凸的，且是一个NP-难问题，一般难以直接求解。在这种情况下，主成分追踪（Principal Component Pursuit，PCP）[12-13]算法被提出，其采用凸松弛逼近的方式解决该问题，即采用核范数逼近传统LRSD模型中的秩函数，采用l1范数逼近传统LRSD模型中的l0范数，成为解决传统LRSD模型的有效算法，并成为人们推进LRSD相关算法发展的基石。

随着计算机视觉等领域的飞速发展，PCP算法在处理数据矩阵时的缺陷也日渐凸显，主要体现在凸逼近程度不高、鲁棒性弱、极少考虑数据矩阵的时空特性等方面[14]。基于这些问题，许多改进的LRSD 算法被陆续提出，并取得了一定的进展。按照逼近方法，可以将常见的LRSD改进算法分为以下两大类：

（1）采用凸函数逼近传统LRSD的改进算法，例如主成分追踪（Principal Component Pursuit，PCP）算法、截断核范数（Truncated Nuclear Norm，TNN）算法[15-20]、去分解（Go Decomposition，GoDec）算法[21]、低秩结构化稀疏分解（Low-Rank and Structured Sparse Decomposition，LSD）算法[22-27]、运动信息辅助低秩稀疏分解（Motion-Assisted Matrix Restoration，MAMR）算法及鲁棒运动信息辅助的低秩稀疏分解（Robust Motion-Assisted Matrix Restoration，RMAMR）[28-30]算法等；

（2）采用非凸函数逼近传统LRSD 的改进算法，例如非凸非光滑非利普希茨优化（Nonconvex Nonsmooth and Non-Lipschitz Optimization，NNNOP）算法[31-32]、非凸非光滑加权核范数（Nonconvex Nonsmooth Weighted Nuclear Norm，NNWNN）算法[33]、非凸低秩稀疏分解（Nonconvex Low Rank and Sparse Decomposition，NonLRSD）算法[34]、广义核范数和拉普拉斯尺度混合（Generalized Nuclear Norm and Laplacian Scale Mixture，GNNLSM）算法[35-38]、广义非凸鲁棒主成分分析（Generalized Nonconvex Robust Principal Component Analysis，GNRPCA）算法[39-43]等。

近年来，常见的针对低秩稀疏分解模型求解的算法包括迭代阈值（Iterative Thresholding，IT）算法[44]、加速近端梯度算法（Accelerated Proximal Gradient Approach，APG）[45]、增广拉格朗日乘子法（Augmented Lagrange Multipliers，ALM）[46]、交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）[47]等。其中，IT 算法是最早用于解决PCP问题的算法，该算法的优点是运算简单且收敛，但是运算时间长；APG算法的提出是为了改善IT 算法的缺陷，该算法的主要思路是将低秩稀疏分解的模型包含的约束条件松弛到目标函数中，最终提高了低秩稀疏分解模型求解的速度；之后，ALM算法被提出来并取得了较好的效果，但该算法使得低秩稀疏分解的问题失去可分解性，对大规模问题不能较好地进行求解；为了解决ALM 存在的缺陷，ADMM 算法被提出，并采用分而治之的思想将原始问题分解成多个可求解的子问题来进行求解，并更新乘子。值得一提的是，本文所介绍的低秩稀疏分解模型的求解算法都是采用ADMM算法。

在深入和系统地研究了LRSD 技术的理论和国内外现有算法的基础上，本文分析了诸多采用凸函数和非凸函数逼近传统LRSD 的改进算法，以PCP、TNN、GoDec、LSD、MAMR、RMAMR、NNNOP、NNWNN、NonLRSD、GNNLSM 和 GNRPCA 算法为研究对象，给出了各个算法的模型及其优缺点，并将这些算法应用于视频前背景分离的实验中，最终通过实验提取的前景效果图、F-measure 值和时间的比较，分别从视觉效果和定量评价两个角度验证了各个算法的优缺点。同时，本文也将上述算法应用于图像去噪实验中，通过各种算法对不同图像的去噪效果图、图像去噪的PSNR 值和FSIM 值，从视觉和量化两个角度验证了各个算法在图像去噪应用中的优缺点。

2 低秩稀疏分解

低秩稀疏分解算法根据其对传统LRSD 模型中秩函数和稀疏度函数的替代函数的凹凸特性，将其分为凸低秩稀疏分解算法和非凸低秩稀疏分解算法。本章将从这两方面对经典的低秩稀疏分解算法展开介绍。

2.1 凸低秩稀疏分解

凸低秩稀疏分解算法是最早提出的用于解决传统LRSD 模型的算法，此类算法凭借其简单易求解、时间成本低、效果较好等优势、成为LRSD 类算法发展之初的主流算法，并在视频前背景分离[48-50]、图像去噪[51]等领域取得了较好的应用效果。典型的凸低秩稀疏分解算法包括主成分追踪（PCP）算法、截断核范数（TNN）算法、去分解（GoDec）算法、低秩结构化稀疏分解（LSD）算法、运动信息辅助的低秩稀疏分解（MAMR）算法和鲁棒的运动信息辅助的低秩稀疏分解（RMAMR）算法。接下来将具体介绍这些算法的模型和优缺点。

（1）主成分追踪算法

主成分追踪（PCP）算法是最早提出用于解决传统LRSD问题的凸松弛算法。该算法分别采用核范数和l1范数逼近传统LRSD模型中的秩函数和稀疏度函数，其模型如下所示：

（2）截断核范数算法

截断核范数（TNN）算法是针对PCP 算法模型中核范数对所有奇异值同时最小化，均等对待所有奇异值的问题提出的一种新的算法。该算法是在矩阵的秩与前r个较大的奇异值相关性不大的理论基础上提出的，它采用截断核范数即min(m,n)-r个奇异值之和替代PCP算法模型中的核范数。TNN算法模型如下所示：

其中，σi(L)表示矩阵L的第i个奇异值。由于上式中的截断核范数是非凸函数，是一个NP-难问题，为了求解该问题，TNN 算法将式（3）转换为如下所示问题：

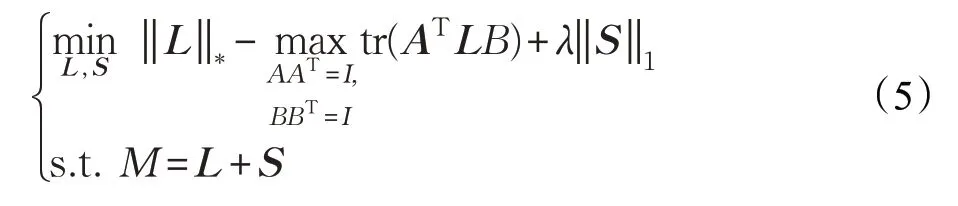
其中，A∈ℝm×r是矩阵L的前r个左奇异向量，B∈ℝn×r是矩阵L的前r个右奇异向量，tr(ATLB)是矩阵ATLB的迹。相对于PCP算法，TNN算法采用截断核范数取得了比核范数更优的逼近程度，低秩稀疏分解的效果更佳，但是在该算法中对r较难做出一个合适的选择决策，最终导致算法不够稳定。

（3）去分解算法

去分解（GoDec）算法是用来解决当数据矩阵在被环境噪声污染的情况下的低秩稀疏分解问题。同时，该算法还采用双边随机投影（Bilateral Random Projections，BRP）算法加速数据矩阵的分解。GoDec算法的模型如下所示：

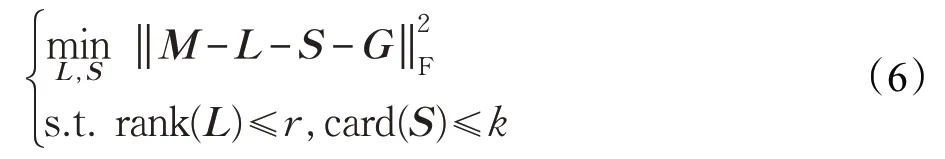
其中，rank(L)为矩阵L的秩，card(S)为矩阵S的势即稀疏度，G为噪声项，r和k分别为秩和稀疏度的最大值。因为该算法使用了BRP，所以极大地降低了低秩稀疏分解算法的复杂度，减少了整个算法的运行时间；同时，该算法模型引入了对噪声项的处理，增加了算法的鲁棒性。但是因为算法中对于r和k值的选择依赖性比较强，所以算法对基于低秩稀疏分解的实际应用场景难以获得一个统一的较好的效果，算法不够稳定。

（4）低秩结构化稀疏分解算法

低秩结构化稀疏分解（LSD）算法认为在许多实际的场景中，数据矩阵中的稀疏部分并不是像素级稀疏的，而是结构化稀疏的，基于这个理论，该算法采用结构化稀疏诱导范数（Structured Sparsity-Inducing Norm，SSIN）来描述数据矩阵的稀疏度。从而最终将数据矩阵理解为低秩成分和结构化稀疏成分的叠加，并在PCP算法模型的基础上提出了LSD算法模型，具体模型如下所示：

（5）鲁棒运动信息辅助低秩稀疏分解算法

运动信息辅助（Motion-Assisted Matrix Restoration，MAMR）低秩稀疏分解算法主要是用于视频前背景分离问题。该算法认为当稀疏部分占整个数据矩阵的比例较小，且变化较快的时候，上述低秩稀疏分解算法具有较好的低秩稀疏分解效果，而在其他情况下，分离效果有限。为了提高在其他情况下的低秩稀疏分解效果，MAMR算法引入了根据运动信息构造的加权矩阵W，该加权矩阵用于最大概率地指示视频对应的数据矩阵的每一个像素是属于低秩的背景还是属于稀疏的前景。在该理论的基础上，MAMR 算法的模型变为如下形式：

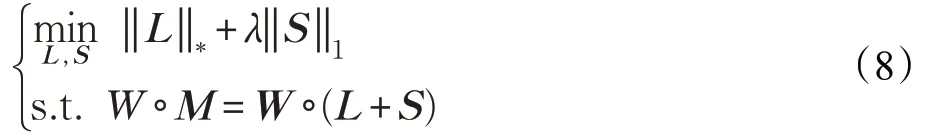
其中，W为根据运动信息构建的加权矩阵，°表示两个矩阵对应元素的乘积。在生成加权矩阵W的时候，该算法采用了与光流法不一样的机制。光流法判断某个像素属于前景还是背景的依据是比较相邻两帧之间该元素是否移动。MAMR算法分两步进行判断：首先，选取参考帧，该参考帧不一定为相邻的两帧；其次，在判断某个像素是前景和背景的时候，是基于离它最近的参考帧，通过判断该像素是否移动，而最终生成运动信息，并映射为加权矩阵W。由于该算法在处理过程中引入了运动信息映射成的加权矩阵，提高了视频前背景判断的准确度，在一定程度上提高了低秩稀疏分解的效果。但是由于在生成加权矩阵的过程中，引入了诸多参数，这些参数在选择过程中，较难达到统一，使得该算法的效果有限。

另外，在实际应用场景中，无处不在的噪声往往会影响低秩稀疏分解的效果，为了提高MAMR 算法的鲁棒性，文献[28]将MAMR算法进行扩展，并提出了鲁棒运动信息辅助（Robust Motion-Assisted Matrix Restoration，RMAMR）低秩稀疏分解算法。该算法将噪声项引入到MAMR模型中，具体模型如下所示：

其中，γ ＞0 为参数，G为噪声项为 Frobenius 范数。RMAMR 算法虽然在一定程度上提高了算法的鲁棒性，增强了模型的抗噪声性，但是没有从根本上解决参数的选择问题，导致在实际场景中低秩稀疏分解效果一般。

2.2 非凸低秩稀疏分解

采用凸替代函数解决传统LRSD 模型的方法凭借其求解简单等优点成为LRSD 发展之初人们研究的热点，但在研究过程中，人们逐渐发现这些凸替代的方法本质上是一种松弛逼近方法，经常会导致过惩罚问题，使得对秩函数或/和稀疏度函数逼近效果有限。在这种情况下，人们逐渐把研究的重心逐渐转向非凸逼近的技术。近几年来，许多典型的非凸低秩稀疏分解算法相继提出并取得了较好的性能，例如非凸非光滑非利普希茨优化（NNNOP）算法、非凸非光滑加权核范数（NNWNN）算法、非凸低秩稀疏分解（NonLRSD）算法、基于广义核范数和拉普拉斯尺度混合（GNNLSM）的非凸低秩稀疏分解算法、广义非凸鲁棒主成分分析（GNRPCA）算法等。接下来，将对这些非凸算法模型进行具体的描述，并给出各种非凸算法的优缺点。

（1）非凸非光滑非利普希茨优化算法

非凸非光滑非利普希茨优化（NNNOP）算法采用了非凸惩罚函数逼近传统LRSD模型中的l0范数，并提出采用通用双步长方法来求解该模型的方法，其模型如下所示：

其中，Ψ(·)和Φ(·)是正常的、闭的、非负函数，Ψ(·)是凸函数，用于替代传统LRSD 的秩函数，一般采用低秩矩阵L的核范数，Φ(·)是非凸、非光滑和非利普希茨函数，用于替代传统LRSD 模型中的l0范数，其表达为其中，φ(·)为非负连续函数，通常可以取lp(0＜p ＜1)罚函数、分数罚函数、log 罚函数、硬阈值罚函数和Concave 罚函数等。 A、B 和C 均为线性映射。在视频前背景分离的实际应用中，该模型的A、B和C 均为单位映射，约束条件退化为M=L+S。

NNNOP 算法采用非凸非光滑和非利普希茨函数Φ(·)替代传统 LRSD 的l0范数，逼近程度高，与基于凸函数逼近类算法相比，低秩稀疏分解效果好。但是，该方法只考虑了l0范数的替代问题，对于秩函数的逼近仍然采用核范数，该方法存在局限性，稀疏低秩分解效果存在可待提升的空间。

（2）非凸非光滑加权核范数算法

非凸非光滑加权核范数（NNWNN）算法认为核范数是传统LRSD模型的凸替代，会引起对所有奇异值同时最小的缺陷，在此基础上，提出了采用非凸非光滑加权核范数逼近传统LRSD的秩函数，其模型如下所示：

由于0 ≤ω1≤ω2≤…≤ωmin(m,n)是非凸的，式（11）的最优化问题为非凸非光滑问题，能较好地逼近传统LRSD 模型中的秩函数。但是该算法采用加权核范数逼近秩函数，不是秩函数的一个较紧的逼近。此外，该模型仍然采用l1范数替代传统LRSD 模型中的稀疏部分，低秩稀疏分解效果仍然存在可以提升的余地。

（3）非凸低秩稀疏分解算法

非凸低秩稀疏分解（NonLRSD）算法为了进一步提高对传统LRSD算法模型中秩函数的替代程度，采用广义非凸代理函数替代秩函数，其模型如下所示：

其中，g(·):ℝ+→ℝ+是连续的、凹的、非递减的函数，可以取Logarithm、平滑切片绝对偏差（Smoothly Clipped Absolute Deviation，SCAD）等罚函数。给出了该算法的收敛性分析，最终通过人工数据、低秩图像去噪声和视频前背景分离等实验验证了NonLRSD算法模型比其他凸的和非凸的算法模型更有效。虽然该算法模型用逼近效果更优的连续的、凹的、非递减的替代函数逼近了传统LRSD模型的秩函数，但是仍没有考虑稀疏部分的最优替代问题。

（4）基于广义核范数和拉普拉斯尺度混合的非凸低秩稀疏分解算法

基于广义核范数和拉普拉斯尺度混合（GNNLSM）的非凸低秩稀疏分解算法针对传统求解LRSD 模型的方法中存在的逼近度非最优的问题，分别采用广义核范数（Generalized Nuclear Norm，GNN）和拉普拉斯尺度混合（Laplacian Scale Mixture，LSM）来替代传统LRSD模型中的秩函数和稀疏函数，提出了GNNLSM 算法模型，其格式如下所示：

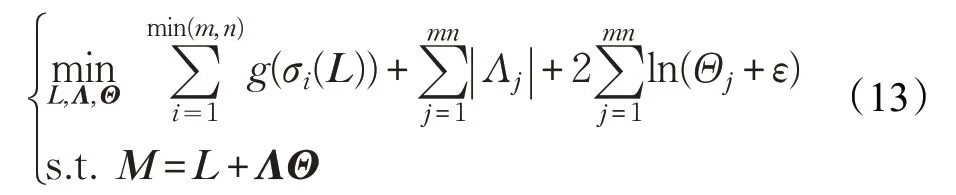
其中，Λj是尺度为1的拉普拉斯分布，乘子变量Θj是一个正的随机变量，ε是一个很小的正的常数。理论表明，LSM比l1范数能更有效地对稀疏度函数进行逼近，同时广义核范数能够取得比核范数更好的逼近秩函数的效果，并且该模型无需手动选择折中参数λ。

（5）广义非凸鲁棒主成分分析算法

广义非凸鲁棒主成分分析（GNRPCA）算法主要是应用于视频前背景分离中，该算法针对当前低秩稀疏分解算法对秩函数和稀疏度函数逼近程度低的问题，分别采用了广义核范数（GNN）和广义范数（Generalized Norm，GN）逼近传统LRSD模型中的低秩部分和稀疏部分，其模型如下所示：

其中，g(·):ℝ+→ℝ+是非凸的、闭的、正常的下半连续函数，可以选Logarithm、lp-norm(0＜p ＜1)、SCAD、最小-最大非凸（Minimax Concave Penalty，MCP）、Geman 和Laplace等罚函数。GNRPCA算法用于视频前背景分离，在实现视频背景建模的同时提取了视频的前景信息。

3 基于稀疏低秩分解的应用实验

3.1 基于LRSD的视频前背景分离

随着大数据时代的到来，视频已经成为信息处理和传输的主要信息载体。视频前背景分离为视频处理的高层应用提供了基础，具有较高的实用价值。低秩稀疏分解理论认为，视频的背景部分帧与帧之间的变化是较小的，满足低秩特性，前景部分仅占整个视频较小一部分，满足稀疏特性，并且前景和背景的关系不大。因此视频前背景分离问题可以转化为低秩稀疏分解问题。

本文为了更具体地描述各低秩稀疏分解算法的优劣，将各算法应用到视频前背景分离实验中，展示了各算法提取的前景图和对应视频前背景分离的F-measure值，不仅从视觉上体现各算法的优劣，更从量化的角度展示各算法的不同，同时提供了各算法进行视频前背景分离的运行时间，验证了各算法的时间复杂度。

实验所使用的计算机硬件环境为i5-5287U CPU@2.9 GHz，实验仿真工具为MATLAB R2018a。实验中所使用的算法为本文介绍的PCP、TNN、GoDec、LSD、MAMR、RMAMR、NNNOP、NNWNN、NonLRSD、GNNLSM、GNRPCA 模型。实验用视频为CDnet 数据集[52-53]和I2R数据集[54-55]中的公共视频，包括Shoppingmall、Watersurface、Escalator、Fountain、Switchlight、Curtain、Highway。

首先，本文采用各算法对不同视频进行视频前背景分离，随机选取各视频对应提取前景的某一帧作为效果展示示例，从视觉角度比较各算法的效果，如图1所示。

从图1可以看出，非凸低秩稀疏分解算法提取的前景噪声较少，例如，从Fountain 视频提取的前景中可以看出，非凸低秩稀疏分解算法提取的前景比凸低秩稀疏分解算法的噪声要少。非凸低秩稀疏分解算法提取的前景信息更加完整，例如，从Curtain视频提取的前景中可以看出，非凸的低秩稀疏分解算法提取的前景中人的信息比凸低秩稀疏分解算法更加完整，尤其是GNRPCA算法提取的前景效果更优。

其次，本文采用F-measure值对各算法处理不同视频的效果进行量化，从量化角度比较各算法的效果。其中F-measure 值为用来评价视频前背景分离效果的标准，其形式为：

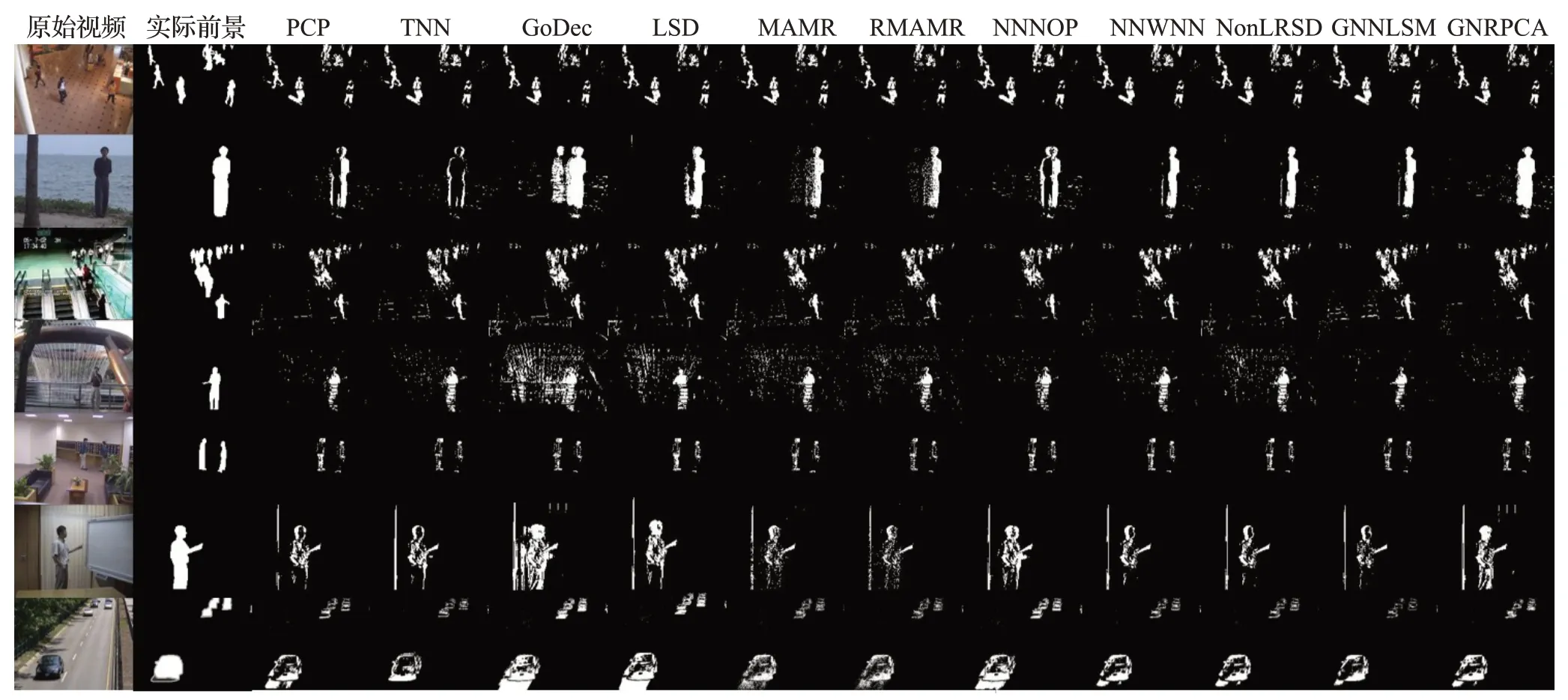
图1 各算法提取的视频前景对比图

从表1的量化数据可以看出，非凸低秩稀疏分解算法的效果要优于凸低秩稀疏分解算法。例如，表1中最高的平均F-measure值为非凸的GNRPCA算法，比最低的凸LRSD的TNN算法提高10%左右。同时，本文五种非凸LRSD 算法提取视频前景的平均F-measure 值为0.592 48，五种凸LRSD 算法提取视频前景的平均F-measure值为0.557 37，进一步验证了非凸LRSD算法的优势。

另外，实验给出了各LRSD算法在视频前背景分离中的运行时间，如表2所示。

从表2可以看出，GoDec算法由于使用了BRP算法，加速了低秩稀疏分解算法，在时间上占有绝对的优势；LSD算法由于引入了结构化信息，并对结构化信息进行相应的处理，其运算时间非常长，是所有算法中执行速度最慢的。

表1 各算法进行视频前背景分离的F-measure值

表2 各算法进行视频前背景分离对应的每帧运行时间 s

综上所述，仿真实验结果表明非凸低秩稀疏分解算法比凸低秩稀疏分解算法具有更好的视频前背景分离效果。

3.2 基于LRSD的图像去噪

图像在存储和传输等过程中难免会受到噪声的污染，随之产生的图像去噪问题[56-58]便成为人们研究的热点。由于图像本身具有非常强的自相关性，故可以采用非局部低秩正则化模型[37]将图像进行转换，使其满足低秩特性，而自然界中的很多噪声例如脉冲噪声等满足稀疏特性，因此可以将低秩稀疏分解[59]方法用于图像去噪。

在图像去噪实验中，本文采用的LRSD算法分别为PCP、TNN、GoDec、LSD、MAMR、RMAMR、NNNOP、NNWNN、NonLRSD、GNNLSM、GNRPCA 算法。实验的对象为加入噪声密度为10%脉冲噪声的Baboon、Boat、Cameraman、Couple、Fruits、Lena 和 Peppers 图像，尺寸大小均为256×256。

为了评价每种算法对不同加噪图像的去噪效果，本文首先展示了各种算法对不同加噪图像的去噪效果对比图，从视觉角度来评价各种算法的优缺点，如图2 所示。从图2可以看出，基于非凸低秩稀疏分解算法效果优于基于凸低秩稀疏分解算法，主要体现在两方面：一方面是基于非凸低秩稀疏分解算法比基于凸低秩稀疏分解算法对图像的去噪效果好，例如TNN、GoDec 算法的去噪效果较差，这两种算法处理的去噪图像仍然存在肉眼可见的大量噪声；另一方面体现在基于非凸低秩稀疏分解算法对图像去噪之后，仍能保持原图像的清晰度，而基于凸低秩稀疏分解算法存在过度去噪现象，例如基于非凸的NNNOP、NNWNN、NonLRSD、GNNLSM和GNRPCA恢复出的图像清晰度比其他基于凸低秩稀疏分解算法恢复出的图像更好。

为了进一步评价各算法在图像去噪方面的优缺点，本文采用峰值信噪比（Peak Signal to Noise Ratio，PSNR）[60]和特征相似度（Feature Similarity，FSIM）[61]对各算法的去噪效果进行量化，其中PSNR和FSIM值越大，表明算法的图像去噪效果越好。表3 为各算法对不同图像去噪的PSNR 值。从表3 可以看出，所有的基于非凸低秩分解算法都比基于凸低秩分解算法的PSNR值要高，其中基于非凸低秩稀疏分解算法的GNRPCA具有最高的PSNR 值。另外，基于非凸低秩分解算法的PSNR 平均值为28.0，而基于凸低秩稀疏分解算法的PSNR 平均值仅为23.5，前者比后者高4.5。表4为各算法图像去噪的FSIM 值。从表4 同样也可以看出，所有的基于非凸低秩分解算法都比基于凸低秩分解算法的FSIM 值要高，其中基于非凸低秩稀疏分解算法GNNLSM具有最高的FSIM值。另外，基于非凸低秩分解算法的总的FSIM平均值为0.90，而基于凸低秩稀疏分解算法的总的FSIM平均值为0.77，前者比后者高0.13。

综上所述，通过对上述实验结果的分析，可以得到非凸低秩稀疏分解算法比凸低秩稀疏分解算法具有更好的图像去噪效果。

4 结束语

本文将当前低秩稀疏分解算法分为凸低秩稀疏分解算法和非凸低秩稀疏分解算法两类，分别给出各具体算法的模型及其优缺点。同时，为了体现低秩稀疏分解算法的实用意义，首先，本文将各种低秩稀疏分解算法应用到视频前背景分离中，从视觉效果和定量评价两个角度展示了各种算法的优缺点；另外，本文也将各个低秩稀疏分解算法应用到图像去噪实验中，并分别从图像的去噪效果对比图、PSNR 值和FSIM 值展示了各种低秩稀疏分解算法在图像去噪中的优缺点。在后续的工作中，将根据当前低秩稀疏分解算法的现状和发展趋势，设计逼近度更高的、鲁棒性更强的和时间复杂度更低的低秩稀疏分解算法，以此来改善视频前背景分离和图像去噪等的效果，进一步提高LRSD类算法的实用价值。

图2 各算法对加噪图像的去噪效果对比图

表3 各算法图像去噪的PSNR值 dB

表4 各算法图像去噪的FSIM值