结合最大最小距离和加权密度的K-means聚类算法

马克勤，杨延娇，秦红武，耿 琳，王丕栋

西北师范大学 计算机科学与工程学院，兰州 730070

1 引言

聚类是数据挖掘[1]领域的一项重要技术，一直受到研究者的高度重视，被广泛应用到很多领域，包括市场研究[2]、数据分析[3]、模式识别[4]、图像处理[5]和文本分析[6]等。传统K-means算法即K均值算法是MacQueen[7]提出的一种经典的基于划分的聚类算法。该算法凭借着原理简单易懂、收敛速度快、执行效率高等优点而被人们广泛使用。但该算法的聚类结果不仅易受聚类数K的影响，而且对初始聚类中心的选择依赖性比较大，不同的初始聚类中心下聚类结果通常不一样，因此算法的稳定性较差；另外聚类中心的选择往往会使聚类结果收敛于局部最优。

目前对K-means算法的研究主要集中在以下方向：一是研究如何通过获得更好的初始聚类中心来改进算法的性能。左进等[8]在数据点紧密性的基础上排除离群点，均匀地选择初始聚类中心，但依然需要根据经验确定K值；汤深伟等[9]将混沌搜索引入到粒子群算法中，将改进的粒子群算法应用到K-means算法中，以此来寻找较好的聚类中心；隋心怡等[10]将样本分布空间分割为大小相同的子空间，通过统计子空间中的样本密度来优化初始聚类中心，实验表明该方法可以有效提高算法稳定性并减少迭代次数，最终获得较好的聚类效果。二是研究如何获得最佳的聚类数，即确定最优的K值。王建仁等[11]针对传统手肘法中“肘点”不明确问题，结合指数函数性质、权重调节、偏执项和手肘法基本思想进行改进优化，实验表明改进算法能有效确定K值，且性能良好；Sun 等[12]提出了基于密度和下一个拟合情况下的K值优化算法，可以高效准确地获得簇的数量K，通过用户合理的阈值设置，大大降低错误并提高簇数K的准确性。三是对中心点和聚类数同时进行改进。张素洁等[13]根据密度和最远距离对中心点进行选取并结合SSE（Sum of Squares for Error）确定最优的K值，最终获得较高的聚类准确率；贾瑞玉等[14]使用密度法选取中心点集，再将聚类离差距离与聚类距离的比值作为一种新的聚类有效性指标IBWP，并依据此指标获得最佳聚类数，从而得到良好的聚类效果，但算法因受聚类数和搜索范围的影响付出了时间代价。

综合上述对传统K-means算法的改进，本文提出了一种基于加权密度和最大最小距离的K-means 算法（K-means algorithm based on Weighted Density and Max-min distance，KWDM），通过加权密度法来确定中心点集，排除离群点对聚类结果的影响，再利用最大最小距离准则来选择中心点，有效地避免了聚类结果陷入局部最优，提高了划分初始数据集的效率，最后利用准则函数即簇内距离和簇间距离的比值来确定K值，使聚类的准确率和稳定性都得到提升。

2 基本概念

2.1 K-means算法

K-means 算法的基本原理是将n个样本集划分到K个簇中，要求划分到同一簇中的样本尽可能地相似，而划分到不同簇中的样本尽可能地相异。

算法基本思想：先随机选取k个样本作为初始聚类中心，计算剩余的每个样本到初始聚类中心的欧氏距离，将每个样本划分到离它最近的聚类簇中；然后对调整后的类簇进行簇类中心的更新，反复迭代直到聚类准则函数收敛或者达到迭代次数。

评价聚类结果通常用误差平方函数作为聚类准则函数，如式（1）所示：

其中，Cj表示第j个类别中的样本集合，vj是Cj内所有样本点pi的聚类中心点，k表示聚类个数。dist(pi,vj)表示簇Cj的对象pi与质心vj在m维空间的欧氏距离，m、l为空间维数，如式（2）所示：

聚类中心的更新如式（3）所示：

其中，n是Cj中数据对象的个数。

2.2 最大最小距离准则

最大最小距离准则[15]是以欧式距离为基础，取尽可能远的样本点作为聚类中心，避免了K-means算法选取初始值时可能出现的聚类中心过于邻近的情况，而且提高了划分初始数据集的效率。算法的基本思想：在样本中首先任选一个样本点作为聚类中心点v1，再选距离v1最远的样本点作为聚类中心v2，选择剩余的中心点l(l＞2)时，分别将剩余的每个样本点到之前中心点的欧氏距离值小的放入集合中，将集合中最大值对应的样本点作为下一个中心点，重复该过程依次计算剩余所需要的中心点，如式（4）所示：

其中，disti1、disti2分别是样本i到v1和v2的欧式距离。

最大最小距离准则找距离远的样本点作为聚类中心，但是仅从距离判断很有可能会将离群点作为初始中心点，从而降低聚类的准确率。

3 KWDM 算法

KWDM 算法基本思想：利用加权密度法排除离群点，选出聚类中心点集；通过最大最小距离准则在聚类中心点集中选取聚类中心；最后利用簇内样本距离与簇间样本距离的比值来确定K值。KWDM 算法克服了K-means算法对聚类中心选择的随机性，防止聚类结果陷入局部最优，同时在欧式距离的基础上加入权值，进一步加强了数据中不同属性的区分程度，减少了离群点的影响，优化了初始聚类中心的选择，提高了聚类结果的准确率。对于K值，文献[16]以距离代价最小原则将K值的范围限定在，实验证明该范围可以提高聚类效率，并从理论上论证了其合理性，因此可以作为本文K值确定的参考。

3.1 权值的计算

算法中权值的计算引用了文献[17]的权值计算公式，相关定义如下：

设有n个样本数据X={x1,x2,…,xn}为聚类数据集，其中xi=(xi1,xi2,…,xim)T为m维向量，根据每个样本数据中每个分量的影响不同，定义权值W=(w1,w2,…,wm)T∈Rn×m，其中wi=(wi1,wi2,…,wim)T为m维向量，权值计算如式（5）所示：

其中，xid表示第i个样本数据中的第d个分量；表示样本数据中各个数据对象的第d个分量中和的平均值；w反映了样本数据整体分布特征。

3.2 所有样本点的平均距离

加权的欧式距离如式（6）所示：

其中，distw(xi,xj)表示样本xi和xj在m维空间下的加权欧氏距离，xil和xjl分别表示在空间l维下的样本xi和xj，m、l为空间维数。

所有样本点的平均欧式距离如式（7）所示：

3.3 K 值的确定

聚类中K值的确定对聚类结果有很大的影响，不同的K值对应不同的聚类结果。聚类结果要求簇内样本距离越小即簇内相似度越高，簇间样本距离越大即簇间相似度越低，则聚类效果越好，也就是说聚类效果跟簇内样本距离和簇间样本距离都有关系。因此本文利用簇内样本距离与簇间样本距离的比值来确定K值，相关定义如下：

定义1 存在n个数据对象的数据集S，假设n个数据对象被划分到K个类簇中，定义第j类对象i的簇间样本距离b(j,i)为该样本到其他每个簇中样本平均值的最小值，如式（8）所示：

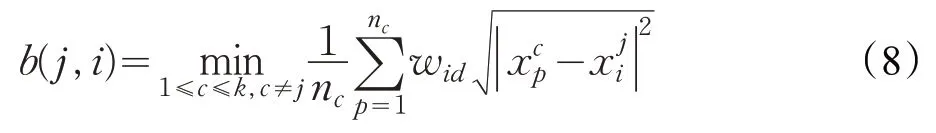
其中，nc表示类c的元素个数，表示第c类的第p个样本，表示第j类的第i个样本，表示加权的不同簇间的样本p到样本i之间的欧式距离。

定义2 存在n个数据对象的数据集S，假设n的数据对象被划分到K个类簇中，定义第j类的对象i的簇内样本距离v(j,i)为该样本到簇内其他样本的平均值，如式（9）所示：

其中，nj表示类j的元素个数，表示第j类的第p个样本，表示第j类的第i个样本，表示加权的簇内的样本i到簇内其他样本间的欧式距离。

定义3 第j类的数据对象i的聚类有效性指标为簇内样本距离与簇间样本聚类的比值，如式（10）所示：

由公式可得，簇内样本距离v(j,i)越小，簇间样本距离b(j,i)越大，则H(j,i)的值越小，聚类效果越好。通过比较聚类样本集n个样本对象的H值的平均值的大小来确定最佳聚类数，则式（11）中指标最小时所对应的聚类数为最佳聚类数，即最佳的K值。

3.4 KWDM算法流程

输入：样本集X。

输出：聚类结果。

步骤1 输入样本点集X，根据式（6）、（7）计算出所有样本点的平均距离avgdistw。

步骤2 以任意样本点x为中心，R=avgdistw为半径画圆，将圆内的所有样本点数目T（包括边缘的样本点）作为样本点x的密度。

步骤3 计算出所有样本点的密度后，按从大到小的顺序将前个样本数据存入到数据集合U中，选取样本点密度最大的点x1作为第一个聚类中心放入中心点集合C中。

步骤4 在数据集合U中找出距离x1最远的点作为第2个中心点x2加入到中心点集合C中。

步骤5 根据最大最小距离准则，在剩余的所有样本中依次计算出-2个中心点，依次加入中心点集合C中。

步骤 6 因为2 ≤K≤，则从集合C中选择前k个数据样本作为初始聚类中心点。

步骤7 将数据集X中的其他样本点根据欧式距离划分到最近的簇中，然后根据式（11）计算本次聚类avgH(k)的值。

步骤8 比较所有不同K的avgH(k)的值，avgH(k)的值最小时，K的取值为最佳聚类数。

步骤9 输出最佳聚类数和对应的初始聚类中心点并进行聚类，算法结束。

4 实验结果和分析

为了检验KWDM 算法的性能，采用随机生成的数值型人工数据集和UCI数据集进行实验。实验配置：操作系统为Win8系统，64位，使用python2.7.0来实现提出的算法，运行环境为Intel®CoreTMi5-7200U CPU，2.50 GHz，8.00 GB。

实验1 随机生成1 000条数值型数据作为数据集散布在解空间，其中每条数据有两个属性，通过对比K-means算法和KWDM 的聚类效果图，验证本文算法聚类中心选取的有效性，经过最大最小距离准则得到聚类类别数为K=6，聚类结果如图1、图2所示。

通过两种算法聚类结果对比，由图1、图2可以看出K-means算法的部分聚类中心分布较为集中，有的簇选取了离群点作为中心点；KWDM 算法通过密度法排除了离群点作为中心点的可能，优化了聚类中心的选取，并通过最大最小距离准则改善了K-means算法易陷入局部最优的问题，相较于K-means算法，聚类中心分布更均匀，聚类效果更佳。

图1 K-means算法聚类结果

图2 KWDM 算法聚类结果

实验2 选取专用于测试聚类算法性能的UCI 数据库中的Iris、Wine 和Seeds 三组数据集进行仿真。其中Iris 数据集样本个数为150，数据属性为4，类数为3；Wine 数据集样本个数为178，数据属性个数为13，类数为3；Seeds 数据集样本个数为210，数据属性个数为7，类数为3。三个数据集的统计信息如表1所示。

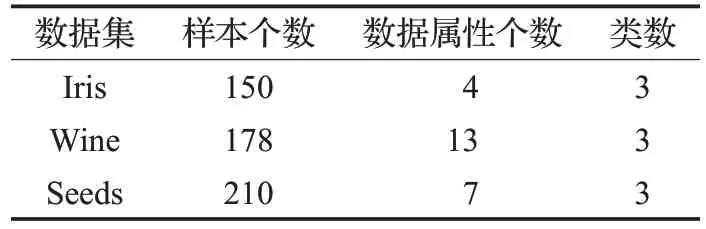
表1 UCI数据集信息

为了验证算法的有效性，K-means算法、文献[10]、文献[11]、文献[13]算法及KWDM 算法分别在三组数据集上进行独立实验，从聚类的准确率、迭代次数及稳定性上进行分析。

表2 显示的是算法的准确率。从表2 可以看出，KWDM 算法得到的平均聚类准确率相较于K-means算法和文献[10]、文献[11]、文献[13]算法分别提高了13.3 个百分点、6.0 个百分点、8.6 个百分点和 3.0 个百分点。也可以看出文献[10]、文献[11]和文献[13]算法优于K-means 算法，这是因为文献[10]和文献[13]算法不再是随机选取初始聚类中心，而是通过空间样本密度来选取初始聚类中心，但是文献[10]算法忽略了离群点对聚类中心的影响，文献[13]算法没有考虑到不同的特征在簇中可能占有不同的比重，文献[11]虽然通过确定K值提高了算法的准确率，但是初始中心点的选取还是随机进行，因此相较于通过密度法来确定聚类中心和对属性进行加权的KWDM 算法来说，其聚类准确率较低。表3 显示的是算法的迭代次数，可以看出KWDM 算法的迭代次数均少于K-means、文献[10]、文献[11]算法。这是因为对选取初始中心的优化，减少了算法的迭代次数，加速了算法的收敛。

表2 算法准确率 %

表3 算法迭代次数

图3、图4、图5 分别统计了五种算法在三组数据集上算法的准确率和迭代次数关系。这充分说明K-means算法和文献[11]算法随机选取初始聚类中心而导致算法稳定性较差，而文献[10]、文献[13]算法和KWDM 算法则可以保持较好的稳定性，且KWDM 算法无论从准确率和迭代次数上都优于文献[10]算法。

图3 Iris迭代次数与准确率关系图

图4 Wine迭代次数与准确率关系图

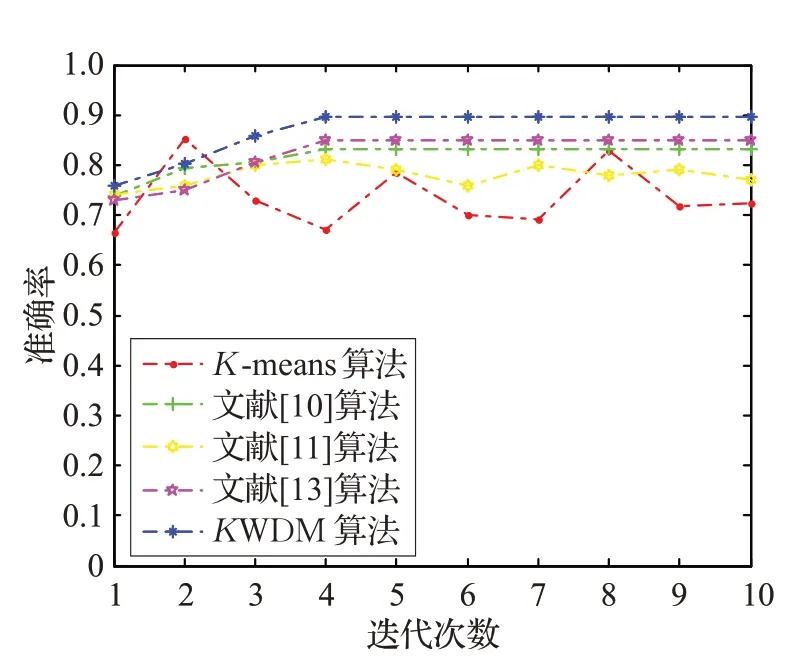
图5 Seeds迭代次数与准确率关系图

算法复杂度分析，K-means 算法的时间复杂度为O(nkT)，其中n为聚类样本个数，k为聚类簇数，T为聚类过程迭代次数。KWDM 与传统K-means 算法相比，聚类过程主要分为两步，其中选择初始聚类中心的时间复杂度为O(2n2),确定K值的时间复杂度为O(nt3/2),因此KWDM 算法整体时间复杂度变为O(2n2)+O(nt3/2),其中t为KWDM 算法的迭代次数。虽然KWDM 算法增加了选择初始聚类中心点这一环节，会造成大量的时间消耗，但是一旦选择到较优的初始聚类中心点，可以减少迭代次数，缩小时间消耗。由图3、图4、图5五种算法在Iris、Wine、Seeds 三种数据集上的迭代次数与准确率的关系图可知，KWDM 算法在迭代次数较小的情况下也能达到较高的准确率，因此t＜T时，KWDM 算法可以减少迭代时间。算法的运行时间如表4所示。

表4 时间复杂度 ms

从表4 可以看出，KWDM 算法的时间复杂度优于文献[10]、文献[11]和文献[13]的时间复杂度。KWDM算法通过密度法来确定聚类中心并对属性进行加权，提高了算法的准确率，但是该算法与K-means算法相比，其运行时间较长。

5 结束语

本文主要针对K-means 算法随机选取初始聚类中心和根据经验确定聚类数而造成的算法不稳定性等问题，提出了一种基于密度和最大最小距离的KWDM 算法，不仅对聚类中心的选择进行了优化，对K值也进行了有效的确定，在欧氏距离的基础上加入了权值，利用密度法来选取初始聚类中心集，减少了离群点对聚类结果的影响，再结合最大最小距离准则，有效地避免了在聚类中心的选取上陷入局部最优的问题。在人工数据集和UCI数据集上的实验结果表明，KWDM 算法不仅在聚类的准确率上有所提高，而且减少了算法的迭代次数，提高了算法的稳定性。但由于KWDM 算法需要统计所有样本空间的分布，从而算法的时间复杂度有所提高，因此在处理高维大数据时，KWDM 算法还需要进一步的改进，这也是今后需要研究的方向。