利用矩阵补全优化模型进行动态网络链接预测

宋光鑫，王丽平

南京航空航天大学 理学院，南京 211106

1 引言

在计算机科学中，网络通常是指一幅节点或连边具有语义的图，它可以挖掘社交网络上的人际关系[1]，电商网站中用户对商品的偏好或生物化学领域蛋白质之间的相互作用。对这样的数据结构进行数据挖掘时，传统的数据挖掘算法通常只考虑网络的节点属性，并将数据中的每个节点视为从某个分布中采样得到的独立同分布个体。这样简单的假设通常会对算法结果造成误导，因此研究节点之间的连边模式变得尤为必要。

在大多数情况下，被观测到的网络结构信息是不完整的，预测网络中两个节点之间是否存在连边将是一个令人感兴趣的问题。另一方面，某些网络中的连边随着时间表现出动态的特性，这样的网络中人们可能会关心某条连边在未来是否会出现。由已观测到的网络结构推测未观测到的网络结构通常被称为静态链接预测，而由过去时刻的网络结构推测未来时刻的网络结构被称为动态链接预测。目前针对静态链接预测提出的预测算法主要包括基于节点相似度[2]、基于最大似然估计[3]和基于概率模型[4]的三大类别。其中最常见的是基于相似度的算法，例如Preferential Attachment Index（PA）、Common Neighbours（CN）、Adamic-Adar（AA）、Katz 等算法[5-6]，这些算法在静态链接预测中显示出了强大的效果，常被用于基准算法。对于静态链接预测的研究还在持续，如伍杰华[7]引入树状数据结构来计算合著者网络结构，并联合朴素贝叶斯算法和节点相似度实现链接预测；张昱等人[8]提出了一种融合网络结构和节点属性的链接预测方法；程华等人[9]关注节点的邻域相似性和依赖关系，提出了基于Attention机制的静态链接预测算法；Pech 等人[10]建立了基于鲁棒PCA（principal component analysis）的矩阵补全模型并应用于静态链接预测；Mohtashemi 等人[11]提出了对数正态矩阵补全模型来求解链接预测问题。相较之下，动态链接预测加入了时间维度，考虑网络结构随着时间的演变，它的预测难度更大。早期的动态链接预测方法主要是将静态问题的算法进行一定的推广。近年来，随着人工智能的兴起，许多机器学习的方法被应用于动态网络链接预测[12-14]。安琛等人[15]将主动学习应用于动态网络链接预测，充分利用了网络中未链接节点的信息。Chen 等人[16]提出监督学习对网络中节点对的结构进行建模以预测未来时刻可能出现的链接。陈阳等人[17]将集成学习引入动态链接，把链接预测看作一个分类问题，通过训练多个分类器来提高类别预测效果，使得网络演变的动态信息得到充分的利用。Xu等人[18]利用监督学习和特征工程的方法关注动态图变化的特征信息，有效提高了预测准确度。Li 等人[19]利用深度学习的方法以及梯度提升树模型挖掘动态链接中隐藏的模式关系。目前，绝大多数动态链接预测论文中提出的动态链接预测方法主要关注网络图随时间演化的特征信息和节点相似性，很少考虑网络结构的稀疏性和在原始空间中难以学习到的非线性链接关系。近年来，稀疏学习和压缩感知得到了深入的研究和应用，Liu等人将其应用到协同过滤当中，并加入核方法来获得在原始空间中不能够学习到的非线性关系[20]。受此启发，本文将矩阵补全方法应用于动态链接预测，并借鉴Liu等人为协同过滤构造核矩阵分解模型的方法，为动态链接预测构造了核矩阵补全模型，通过将原始数据映射到高维Hilbert空间，再应用矩阵补全模型来学习到更多的链接信息，提高模型的预测效果。

2 链接预测问题

2.1 静态链接预测

静态链接预测问题是在已知网络的节点和连边的条件下预测未观测到的连边。设已观测网络G=(V,E)，其中V代表所有节点的集合，E代表已观测到的连边的集合，用N和M分别代表网络中节点和连边的数目。网络的邻接矩阵用A∈{0,1}N×N表示，Aij=1代表节点对(i,j)上存在一条连边（从i指向j），即(i,j)∈E。记所有的节点对构成的集合为U=V×V，链接预测问题就是要对一开始未观测到连边的节点对(i,j)∈UE，给出其实际存在链接的可能性。静态链接预测的算法为每一个节点对(i,j)∈UE给出一个存在链接的得分值score(i,j)，然后对每一个得分值进行排序，得分越高的节点处越有可能存在链接。常用的静态链接预测算法大多根据节点之间的相似度来排序得到最可能存在链接的节点对，具有代表性的算法如引言中所述，有CN、AA、PA 等。其中，CN 算法统计网络图中每个节点的邻接节点，并计算每对节点的公共邻接节点的数量作为它们可能产生链接的分数。AA 算法则在CN算法的基础上添加了节点权重系数。PA算法认为节点x产生新的节点的概率与它的邻接节点数量| |Γ(x) 成正比，那么节点x与节点y存在链接的概率则正比于。

2.2 动态链接预测

对于动态链接预测问题，已观测数据通常是网络在一段时间T内的演变序列{G1,G2,…,GT}。其中Gt=(V,Et)是网络在t时刻的链接状态，V是前T个时间序列中出现过的节点集合，Et则是t时刻网络中连边的集合。网络序列的邻接矩阵A∈{0,1}N×N×T是单幅网络邻接矩阵在第三个维度上叠加得到的。即Aijt=1表示节点对(i,j)在t时刻具有链接。动态链接预测问题需要根据前T个时刻的网络序列Gt(t=1,2,…,T)的邻接矩阵At来预测T+1 时刻的邻接矩阵At+1，从而得到Gt+1。许多如CN、PA、AA等基于邻域的算法可以简单地推广到动态链接预测问题上。推广方法为视AT为一个静态邻接矩阵而直接对AT应用相应的算法，更常用的方法是定义网络Gtotal的邻接矩阵Atotal，Atotal在任意时刻出现过的连边均视为在Atotal上存在，再对Atotal应用静态链接预测算法得到At+1。这种直接将静态链接算法推广到动态中的方法虽然简单，但实验表明，往往具有很好的效果[1]。此外，Chakrabarti等人建立了一种根据邻域相似性的非参数估计模型[21]来求解动态链接预测。该方法对某个节点和其他节点产生连边的概率展开研究，并认为具有相似邻域的节点产生连边的概率相等，通过同时利用时间和空间上的拓扑结构对链接出现的可能性进行预测。出于相同的目的，Hisano提出了半监督图嵌入的方法[14]，通过定义在时间序列上的监督损失和网络状态上的无监督损失，来获得时间和空间上的信息，以达到动态链接预测的目的。

3 矩阵补全与核化矩阵补全

3.1 标准矩阵补全算法

2.2节所述的动态链接预测算法虽然考虑了时间维度的变化信息，但却忽略了邻接矩阵的结构特征。一般地，真实世界中的一幅大规模的网络邻接矩阵，在某个时间段内节点与节点之间的互动是非常有限的，而节点与节点之间产生链接又具有较强的相关性，因此网络图的邻接矩阵具有低秩性和稀疏性。矩阵补全是指，对一个大小为n1×n2的矩阵，在采样得到矩阵中m个元素的情况下，根据一定的假设条件和优化方法来计算出其他未观测到的元素的数值。近年来，有部分学者将矩阵补全应用于静态链接预测问题，如Pech等人将鲁棒PCA的矩阵补全求解方法用于静态链接预测[10]，Gao 等人则提出交替迭代的矩阵补全模型求解静态链接预测[22]。动态链接预测是根据图Gt预测图Gt+1，一个自然的想法是把Gt和Gt+1叠加看作一张完整的图G，而Gt作为已观测到的网络结构，定义增加矩阵Ft+1=Mt+1-Mt,M表示网络链接预测中的邻接矩阵，那么Mt表示t时刻网络的邻接矩阵。在已知矩阵Mt时对Gt+1的预测就是对Ft+1的预测，即根据已观测到的元素来预测G中隐藏的链接，这等价于静态链接预测。静态链接预测与动态链接预测的这种相似关系启发本文将矩阵补全应用于动态链接预测问题。

定义某个网络结构在时刻t的邻接矩阵为Mt，为了预测下一时刻的邻接矩阵，建立动态网络链接预测的矩阵补全模型：

式中，PΩ(·)是采样算子，将不在采样集Ω中的矩阵元素置为0，其他元素不变。在链接预测问题中，令采样集为邻接矩阵中已存在链接的位置集合，这里不考虑链接权重，则设Mij=1,(i,j)∈Ω,PΩ(Mt)视为在时刻t的邻接矩阵，动态链接预测问题往往关注新产生的链接位置，那么不妨认为从时刻t到时刻t+1 在观测集内的链接依然存在，并根据t时刻链接结构推测t+1 时刻在观测集Ω外哪些位置会发生链接。由（1）求出的矩阵X就是对采样集外所有位置产生链接可能性的打分，数值越大代表越有可能产生链接。λ是需要手动设置的参数，λ越大代表越重视矩阵的低秩约束[23]。

模型（1）是一个关于X的矩阵LASSO 问题，目前求解无约束最优化模型的优化算法已非常丰富，本文使用加速近端梯度下降法[24]求解矩阵补全模型。另外，为了更多地利用以往时刻网络的结构信息，不妨将以往多个时间片段的邻接矩阵进行叠加来作为待补全矩阵，则（1）可以写为如下形式：

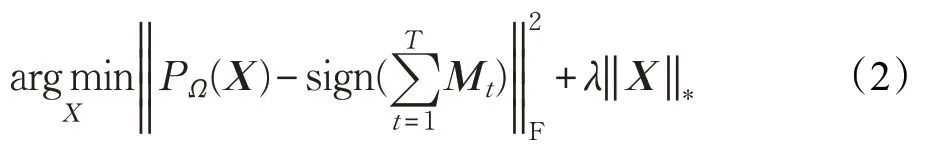
式中，T表示要使用的过去的历史时刻数量，用T个邻接矩阵来预测下一时刻的邻接矩阵。这里将T个邻接矩阵相加，因为本文不考虑链接权重，所以将链接产生的位置数值设为1，使用符号函数sign(·)对做相应处理。为了符号表述的整洁，将（2）改写为更一般的形式：

式中，A(·)：Rm×n→Rp是将所有在采样集Ω中的矩阵元素按列展开拉成一个列向量的算子，Ω={(i,j)|加速近端梯度下降算法的工作原理已得到充分的研究[24]，调用相应的优化算法包即可完成运算。在此简单列出它的迭代公式：

将模型（3）代入框架（4）中，则框架中会出现如下子问题：

子问题（5）存在闭式解[25]，该解可以通过奇异值分解求得。若A的奇异值分解为A=UΣVT,Σ=diag(σi),则其闭式解为X=U[diag(σi-λ)+]VT，即将所有奇异值都减去λ，被减后小于0 的置为0。这相当于给奇异值设定了一个阈值，所有小于这个阈值的奇异值被消减为0，这样就使得矩阵中的非零奇异值数量减少，从而得到降低矩阵的秩的目的。以下给出了求解的完整步骤。由于使用加速近端梯度下降法求解网络链接预测的矩阵补全模型，本文将该算法称为APG（Accelerated Proximal Gradient）算法。

算法1 APG 算法：用加速近端梯度下降算法求解矩阵LASSO问题（3）

输入：采样算子A(·)、采样集b、系数λ、步长μ、最大迭代次数k_max。

输出：Xopt。

初始化：X0=X-1=0m×n,t0=t-1=1,k=0,1,2,…,k_max

1.

2.Ak=Yk-μkA*(A(Yk)-b),其中A*是A的逆算子

3.A奇异值分解，得到U,diag(σ),V

4.Xk+1=U[diag(σi-μkλ)+]VT

5.

6.k=k+1,若满足收敛条件则输出Xk,否则回到步骤1。

由APG算法得到的X是对增加矩阵FT+1的预测，由MT+1=MT+FT+1，就得到了对下一时刻邻接矩阵的预测。

3.2 核化矩阵补全

网络链接预测关注节点之间的相似性，而真实世界的网络链接具有稀疏性和相关性，由矩阵分解的知识可以将网络的一个邻接矩阵看作两个低秩矩阵内积的形式，即X≈UTV，这种分解需要保证在已观测位置(i,j)∈Ω上信息相似，则（2）可转化为如下形式：

式中，U,V∈Rk×n为分解得到的两个低秩矩阵，M表示上一时刻的邻接矩阵。则模型（6）表示用两个低秩矩阵来补全矩阵M。传统的矩阵分解方法通常假设相关链接数据分布在一个线性超平面上。然而，随着真实世界中网络结构愈发复杂，许多网络邻接矩阵不满足低秩性要求，很难通过线性矩阵分解的模型来预测未来的链接结构。为了克服这一困难，本文将核方法引入矩阵补全模型中。核方法考虑把链接数据嵌入一个更高维的特征空间，在这个空间中链接数据可以分布在一个线性超平面上，这使得邻接矩阵可以被表示为两个特征矩阵内积的形式。为了引入核方法，首先令φ(x)为将某个向量x映射到高维特征空间后对应的特征向量，内积＜x,y ＞相应地变为＜φ(x),φ(y)＞，进一步引入核函数：

核方法将链接数据嵌入到高维特征空间H 中，这个嵌入映射是隐式的，但可以由核函数定义。假设某个核函数对应的特征空间映射为φ:X→H，其中X 是原始空间，H 是Hilbert空间，则特征空间中的特征矩阵内积可以通过核函数，利用原空间中的向量计算。引入核技巧后，使用Hilbert 空间中向量构成的矩阵φ(U) 和φ(V)代替原特征空间中的U、V，将问题（6）改写为：

矩阵U、V是需要求解的目标，而非观测到的数据，无法通过核函数直接求解φ(U)Tφ(V)。为此本文通过引入字典向量来代替直接求解U、V。因为在无限维Hilbert 空间中，特征矩阵被映射到线性超平面中，链接数据之间的非线性关系被转化为线性关系，根据泛函分析的知识可知，任何一个Hilbert空间都有一族标准正交基，则特征矩阵可以由一组基线性表示[26]。受字典学习相关理论的启发[27]，本文使用φ(di)的线性组合来逼近矩阵φ(U)，通过建立形如的带正则化项的字典学习模型来求得最优的φ(di)，从而求得φ(U)Tφ(V)。具体地，给定k个d维字典向量d={d1,d2,…,dk}，di∈Rd，那么可以假设低秩矩阵U的每一列uj对应的特征向量φ(uj)均可被字典向量d在特征空间中线性表示为如下形式：

其中，aij为每个字典向量的权重系数，φ(di)为字典向量d的第i个分量di在特征空间中对应的特征向量，ai=(ai1,ai2,…,aik)T,Φ=(φ(d1),φ(d2),…,φ(dk)) 。同样，将矩阵V的每一列vj表示为：

同样，bij为每个特征向量的权重系数，bi=(bi1,bi2,…,bik)T。将权重向量a和b按行叠成矩阵A、B，记：

由于无法直接求解φ(U)Tφ(V) ，通过引入字典向量，将特征矩阵φ(U)、φ(V)转化为字典矩阵Φ的表达式，这样可以得到ΦTΦ，也就构造出了核矩阵。

同时注意到：

根据式（9）～式（12），可以将模型（8）重写为：

其中，K=ΦTΦ是字典向量导出的核矩阵。为了求解模型（13），本文采用交替最小二乘法，其收敛性可以参考文献[28]。算法的具体步骤是，首先固定U，即保持矩阵A不变，可以将（13）按列分解为n个子问题：

其中，Ωj={i|(i,j)∈Ω}表示原矩阵M在第j列上观测到的行i元素组成的集合。约定算子PΩj仅对行进行操作，即PΩj(X)将保留X的所有i∈Ωj行整行，其余元素设为0。类似的用Ωi={j|(i,j)∈Ω}表示在矩阵R第i行上观测到的列j元素组成的集合，PΩi(X)将保留X的所有j∈Ωi行整行。m:,j、vj分别表示矩阵M、V的第j列。

问题（14）是一个类似岭回归的问题，其闭式解为：

其中，A:,Ωj为保留矩阵A的i∈Ωj列得到的子矩阵，m:.Ωj表示由原矩阵M的Ωj个元素构成的列向量。将n个按列的方向组成矩阵对应地可以获得，其中为：

其中，B:,Ωi=PΩi(BT)T为矩阵B的j∈Ωi列构成的子矩阵。m:.Ωj表示由M的Ωi个元素构成的列向量。

交替使用式（15）、（16）迭代更新B、A直至收敛，最终得到A*、B*后，即可通过X*=A*TKB*得到X*作为矩阵补全的结果。以下给出了算法流程，为了叙述方便，将该算法命名为KMC（Kernelized Matrix Completion）算法。

算法2 KMC算法：求解模型（13）

输入：待补全矩阵M，字典向量d，核函数κ。

输出：M≈X=ATKB。

随机初始化A、B

计算核矩阵Kij=κ(di,dj)

Repeat

根据（15）更新B

根据（16）更新A

Until收敛条件满足或达到最大迭代次数

ReturnX=ATKB

许多研究常使用奇异值阈值法求解矩阵补全问题，如将问题（1）中的矩阵X写为奇异值分解的形式：

其中，σi是矩阵X的按降序排列的奇异值，Σ为其构成的奇异值矩阵。奇异值阈值法通过近端梯度下降法，在使得X能近似M的前提下，不断通过奇异值阈值算子将X较小的奇异值置为0 来保证X的低秩性[25]。将式（17）的核范数进行变形得：

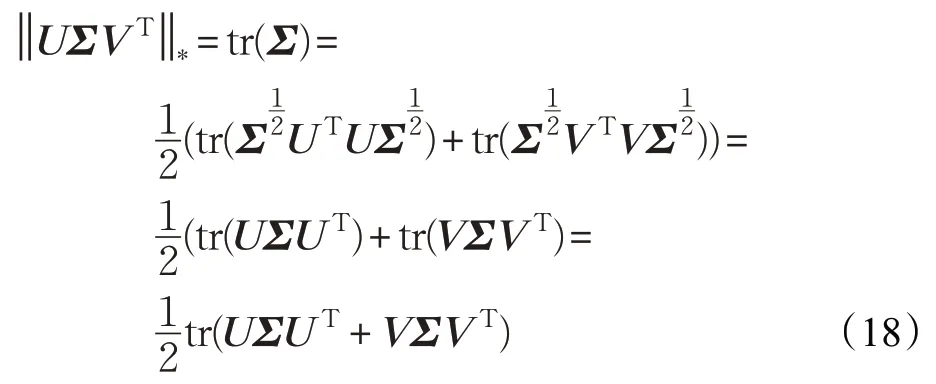
省略系数整理得：

不难看出，KMC 模型（13）与（19）具有一定的相似性。事实上，若设问题（19）的最优解为U*、Σ*、V*，对模型（13），若核矩阵K恰为Σ*时，则可表示为：

这说明KMC模型符合一般的矩阵补全模型。对于矩阵分解模型（6），若取矩阵-Σ∈Rk×n，令：

4 实验

4.1 实验环境和数据信息

为了检测本文提出的算法的效果，挑选了三个真实世界的动态网络链接数据进行实验。实验中使用PA、CN 两种静态链接算法和Pech 等人提出的鲁棒PCA 的矩阵补全模型法做对比。本文实验代码由作者使用Matlab2018a 编写。运行环境为Win10，Intel®Core™ i7-4510U CPU@2.0 GHz，8 GB内存。

表1给出了实验数据集的特征信息。WorldTrade记录了58 个国家的国际贸易情况的数据，记录时间为1981—2000年，若对每年所有国家之间的贸易额度进行排序，取贸易额前10%国家，视为两国之间存在链接，这样可以通过数据集建立20 个58×58 的邻接矩阵。表中总链接数是20 个邻接矩阵所有产生链接的个数总和，时期平均链接数是单位时间矩阵中存在链接数的平均值。EmailEu-core 是欧洲某个大型研究会的邮件系统，记录了研究会1 005名成员的邮件往来。本文选取研究会中两个部门的核心成员在550 天内的邮件往来记录进行实验，其中每50天作为一个时间单位，则可得到11个n×n的动态网络（n为部门核心成员数量）。

表1 数据集信息

本文采用AUC（Area Under ROC Curve）作为评价指标。假设正类样本数量和负类样本数量分别为M和N，首先按照输出值对所有样本从低到高排序并对每个样本赋予一个排名rank，输出值最低的元素rank为1，输出值最高的元素rank为M+N，然后AUC可以通过以下公式计算：

4.2 实验参数设置

对于APG和KMC算法，二者都用到了平衡低秩约束与采样约束的正则项系数，即目标函数（3）和（13）中的λ，这类参数的选取已得到较详细的研究，本文按文献[24]所得出的结论将其设置为。

4.2.1 使用到的历史时刻长度T

首先可能会对算法产生影响的参数是算法所使用的时间序列长度T。直观上，利用越多的历史时刻可以获得越多的网络结构变化的信息，数值实验也基本符合这一推断，图1展示了本文提出的核矩阵补全算法分别在三个数据集上的实验效果。三条折线的整体趋势是上升的，标准矩阵补全算法（APG）的实验结果与图1类似。因为数据集能提供的网络随时间的变化信息总是有限的，所以当选取过多的历史时刻进行训练时可能会造成信息的冗余而产生过拟合，AUC 分数并不会随着时刻数量线性增长。为了尽量少地使用历史时刻长度以节省计算开销，KMC算法建议采用3～5个历史时刻。

图1 时间序列T 对结果的影响

4.2.2 字典向量维度d

图2 字典向量维度d 对结果的影响

字典向量的维度d是本文提出的KMC算法需要用到的超参数之一。图2展示了KMC算法在三组数据集上AUC 随d的变化情况。一般认为，字典向量的维度越高，越能得到更多的链接信息，但是图2 在三组数据集上的实验结果，AUC分数在小范围内波动，算法对参数的选取不敏感。这是由于字典向量被嵌入到高维Hilbert空间当中，算法总是能捕捉到高维空间中的链接信息，使得对d的选取不敏感。最终在三组数据集上选取d=200 来进行数值实验。

4.2.3 矩阵A、B 的秩k

对于KMC 算法在初始化时设置低秩矩阵A、B的秩k。由图3结果可知，对于WorldTrade和EmailEu_Dep2的实验，结果基本稳定在一个较高的得分，在k值选取很小时，符合矩阵的低秩假设和矩阵补全的要求，当k增大时，低秩矩阵A、B的秩并不会随着k的增加而线性增长，这是因为正则化项的约束作用，所以预测结果仍然维持在最优的水平。对于EmailEu_Dep1出现了在k=2～6 时分数较低的现象，可能是因为网络结构存在低秩特征矩阵难以捕捉的信息。

图3 参数k 对结果的影响

4.2.4 核函数的选取

KMC 算法中将数据嵌入更高维度的空间，而高维空间由核函数隐式地确定，因此选取不同的核函数就确定了链接数据不同的嵌入方式，即从不同的角度体现数据的分布规律。表2中MC算法是不使用任何核函数的矩阵补全算法，其余为使用线性核、高斯核、拉普拉斯核的矩阵补全算法。

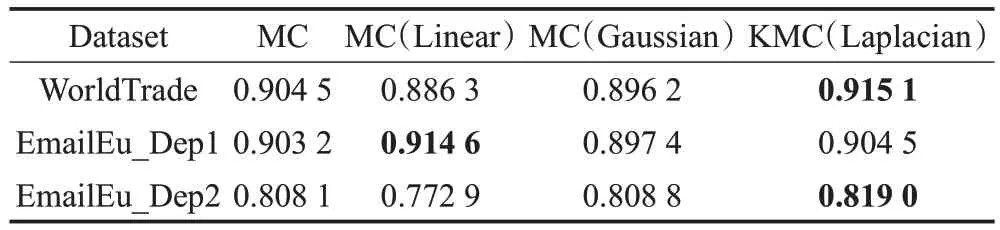
表2 不同核函数在数据集上的AUC分数

从表2可知，拉普拉斯核的算法在所有实验中分数均高于不使用核函数的MC算法，这验证了使用核技巧的有效性。部分实验中也出现了高斯核与线性核算法的效果不如不使用核技巧算法的情况，这可能是由于不合适的核函数不能体现该数据集的分布规律，在映射到高维空间后损失了原始空间中的有效信息，使得核技巧的效果较差。由于每组数据上KMC（Laplacian）的分数均高于MC，这表明Laplacian 核函数能有效地刻画数据的分布规律，确定的高维空间能够更有效地将非线性链接关系转化为线性关系。因此在对比实验中选取Laplacian核作为默认参数。

4.3 实验结果

综合以上实验参数的分析，将三组实验的最优参数的结果列入表3，作为比较实验时的推荐参数。

表3 KMC算法的参数设置

在比较实验结果时，本文使用静态链接预测中常用作基准算法的PA、CN 作为参照，其中CN、PA 是指只使用前一时刻网络结构的算法，CN-all、PA-all是指使用所有历史时刻片段进行预测的算法，它们都是将静态链接预测算法直接应用于动态链接预测。RPCA（Robust PCA）是由Pech提出的基于鲁棒PCA的矩阵补全算法。APG 是指本文提出的利用加速近端梯度下降法求解矩阵补全的算法，KMC是本文提出的核矩阵补全算法（默认使用Laplacian核）。

表4表示所有算法在三组数据集上的AUC分数，本文提出的KMC算法在前两组实验中的AUC得分最高，APG也有较好的表现。在第三组实验中CN_all的AUC得分最高，KMC略弱于基准算法，但CN_all需要使用以往所有历史时刻的网络邻接矩阵，计算存储要求较高，不适合处理大规模链接预测问题。RPCA 通过建立噪声矩阵和原始矩阵求解链接预测，本质上属于矩阵补全模型，因此预测效果与APG相差不大。但由于KMC在矩阵补全模型的基础上加入核函数，能够学习到链接之间的非线性关系，因此KMC效果略好于RPCA，实验结果也验证了使用核方法的有效性。

表4 多种算法在三组数据集上的实验结果

5 结束语

针对传统矩阵补全解决链接预测的局限性，本文提出了KMC 算法，以解决动态链接预测问题。详细介绍了矩阵补全和核矩阵补全优化模型，并推导了核矩阵补全方法与基于奇异值阈值的矩阵补全方法之间的关系。在三组公开的数据集上进行实验，结果表明，KMC算法优于传统的链接预测算法和矩阵补全算法，通过与MC、RPCA算法进行对比，验证了引入核函数的有效性。

本文将拉普拉斯核作为核矩阵补全模型中的核函数，优于基于其他常用核函数的预测效果。未来考虑将如何自适应地选取核函数和提高核函数对非线性关系的刻画能力作为下一步的工作。