Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights

Hi-to Chen , Wen-chun Wng ,*, Xio-nn Chen , Lin Qiu

a School of Water Resources, North China University of Water Resources and Electric Power, Zhengzhou 450046, China

b Construction and Administration Bureau of South-to-North Water Diversion Middle Route Project, Beijing 100038, China

Abstract Based on conventional particle swarm optimization(PSO),this paper presents an efficient and reliable heuristic approach using PSO with an adaptive random inertia weight (ARIW) strategy, referred to as the ARIW-PSO algorithm, to build a multi-objective optimization model for reservoir operation. Using the triangular probability density function, the inertia weight is randomly generated, and the probability density function is automatically adjusted to make the inertia weight generally greater in the initial stage of evolution, which is suitable for global searches.In the evolution process,the inertia weight gradually decreases,which is beneficial to local searches.The performance of the ARIWPSO algorithm was investigated with some classical test functions,and the results were compared with those of the genetic algorithm(GA),the conventional PSO, and other improved PSO methods. Then, the ARIW-PSO algorithm was applied to multi-objective optimal dispatch of the Panjiakou Reservoir and multi-objective flood control operation of a reservoir group on the Luanhe River in China, including the Panjiakou Reservoir, Daheiting Reservoir, and Taolinkou Reservoir. The validity of the multi-objective optimization model for multi-reservoir systems based on the ARIW-PSO algorithm was verified.

© 2020 Hohai University. Production and hosting by Elsevier B.V. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Keywords: Particle swarm optimization; Genetic algorithm; Random inertia weight; Multi-objective reservoir operation; Reservoir group; Panjiakou Reservoir

1. Introduction

Optimal operation of a reservoir alleviates regional drought, flooding, and other natural disasters and plays an important role in the realization of the sustainable development strategy of water resources (Chang and Chang, 2009;Kumar and Reddy, 2007; Yang et al., 2016a; Kang et al.,2019). A reservoir system serves multiple targets, including water supply, flood control, power generation, ecological water supply, irrigation, and so on. Multi-objective problems should be considered in the optimal operation of a reservoir to maximize the comprehensive benefits. With the development of society and economy, people have increasing demands for water resources. However, it is difficult to balance the relationships among various profit-making objectives so as to achieve optimal comprehensive benefits (Yang et al., 2016b).

In the past, many scholars have used a series of typical methods,such as linear programming,nonlinear programming,and dynamic programming, to solve multi-objective reservoir operation problems (Zhao et al., 2011; Zhao and Zhao, 2014;Liu et al., 2011). The dynamic programming approach suffers the curse of dimensionality, whereas nonlinear programming methods have the limitations of the slow rate of convergence(Yeh, 1985). Moreover, traditional nonlinear programming methods have some drawbacks, such as the slow convergence rate, large computation load, and liability to falling into local optima (Bai et al., 2015; Huang and Yuan, 2004).

With the maturity of artificial intelligence and computer technology, heuristic optimization methods have been widely used in reservoir optimal operation research,and they provide a more flexible and efficient tool for solving the optimization modelforlarge-scalereservoirgroupsundercomplexconstraints.At present, intelligent optimization algorithms, such as the genetic algorithm (GA) (Goldberg, 1989; Oliveira and Loucks,1997;Wardlaw and Sharif,1999;Jothiprakash and Arunkumar,2013), particle swarm optimization (PSO) (Eberhart and Kennedy,1995;Chen et al.,2008),and ant colony optimization(ACO) (Dorigo et al., 1996), are being developed rapidly for multi-objective operation models of reservoirs and reservoir groups.Labadie(2004)suggested advanced models for optimization of operation and management of a reservoir system using the heuristic method and GA. Li et al. (2015)established a hierarchical multi-reservoir optimization model for the Three Gorges Reservoir.Chang(2008)proposed rational guidelines for reservoir flood control based on the penalty-type GA.Chaves and Chang(2008)suggested an intelligent reservoir operation system with evolving neural networks.Zheng et al.(2013)employed an improved GA to study the optimal generation dispatch of a multireservoir system. Xu et al. (2005) studied reservoir optimal operation using ACO. Peng and Xue (2011) suggested the generalized ACO in optimal operation of cascade reservoirs.Bai et al. (2015) proposed an improved multi-objective algorithm based on feasible search space optimization to solve the model of cascade reservoirs. Cheng et al. (2008) took advantage of the hybrid GA and chaos to optimize hydropower reservoir operation.In addition,various adaptive optimization algorithms have been presented and applied in reservoir optimal operation(Salazar et al.,2017;Hadka and Reed,2013).Vrugt et al.(2009)proposed a self-adaptive multi-objective method, searching for global optimization in real-parameter spaces. Mirjalili et al.(2014) suggested the grey wolf optimizer. Mao et al. (2019)established shuffled complex evolution coupled with stochastic ranking for reservoir scheduling problems.

The PSO algorithm is an effective optimization method developed in recent years with the advantages of fast convergence and high accuracy(Kong et al.,2017).At present,PSO and related improved methods have been widely used in reservoir optimal operation. Chang et al. (2010) developed a modified adaptive PSO for optimal operation of a hydropower station.Kang et al. (2019) suggested a nonlinear safety degree flood control strategy and applied the model to multi-reservoir systems on the upper Yangtze River. Chang et al.(2013)employed the PSO algorithm and GA to optimize water resources utilization.Zhan et al. (2009) suggested an adaptive PSO based on the standard PSO, and compared it with common improved PSO algorithms.Ma et al.(2018)established a parallel PSO based on Spark multi-objective optimal scheduling of a reservoir group.Zhang et al.(2017)introduced a downhill search strategy into the PSO algorithm to solve the reservoir optimal dispatching model.

Based on analysis of the influence of inertia weight on search capability, a new adaptive random inertia weight(ARIW)strategy for the PSO algorithm(hereinafter referred to as ARIW-PSO) is proposed in this paper. Several typical benchmark functions were used to verify the effectiveness of this method.To illustrate the practical results of this method,a reservoir optimal operation model based on ARIW-PSO was applied to the multi-objective optimal operation of a single reservoir and a reservoir group on the Luanhe River in China.

2. Particle swarm optimization

2.1. Conventional PSO algorithm

In 1995, Eberhart and Kennedy originally put forward the PSO algorithm, which was inspired by the social behavior of bird flocks during food catching (Shi and Eberhart, 1998).Similar to other evolutionary methods, PSO initializes particles by generating a large number of feasible solutions randomly, which are described with vectors.

Assuming ann-dimensional search space, theith feasible solution, called theith particle, is described with anndimensional vector, Xi= （xi1，xi2，…，xin）. The optimal position of theith particle is represented as Xpi= （xpi1，xpi2，…，xpin）, corresponding to the individual optimum. The best particle in the swarm is denoted as XG= （xg1，xg2，…，xgn）, corresponding to the global optimum. The velocity of theith particle is denoted as Vi= （vi1，vi2，…，vin）. With the superscriptkrepresenting the number of iterations, the following operations are performed in the evolution process of the swarm:

whered=1， 2，…，n;i=1， 2，…，N,andNis the size of the particle swarm;wis the inertia weight;c1andc2are positive constants, both generally specified to be 2; andr1andr2are two random numbers, uniformly distributed in [0,1].

The conventional PSO algorithm usually uses the strategy of linear decreasing weight (LDW) to regulate the weight of each particle(Shi and Eberhart,1998).The inertia weight of a particle afterkiterations is described as

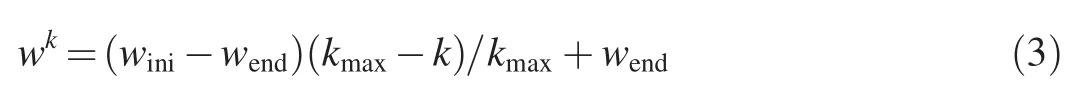
wherekmaxis the maximal iteration number,winiis the initial inertia weight of a particle,andwendis the inertia weight at the iteration numberkmax. Although the PSO algorithm is faster than other evolutionary algorithms in searching for the optimal solution, it faces the problems of premature convergence and poor fine-tuning ability. In the early stage of evolution, particles tend to fall into local optimum because of the small inertia weight. In contrast, in the later stage, because of the large inertia weight, the fine-tuning effect of particles is weak, and the optimal solution may be missed.

2.2.PSO algorithm with adaptive random inertia weights

To improve the performance of the PSO algorithm, an ARIW strategy is proposed. Inertia weights are randomly generated by a triangular probability density function and updated with evolution. In the early stage of the search, the probability of getting a larger weight is very high, which is conducive to global searches. As the number of iterations increases, the probability of obtaining a smaller weight increases, which is helpful to local optimization.

The inertia weight is calculated based on the theorem about Monte Carlo simulation. Supposing thatF（W） is the distribution function of ann-dimensional random variable W, with W = （w1，w2，…，wn）,its inverse function can be expressed as W =F-1（U）. For a uniformly distributed random variable U = （u1，u2， …，un）, with each componentuiuniformly distributed in [0,1], each component of the random variable W, corresponding to the random inertia weight in this study,can be expressed aswi=F-1（ui）, wherei= 1， 2，…，n.

The inertia weightwof the conventional PSO algorithm is calculated with Eq.(3),withk=1， 2，…，kmax.Then the probability density functionfk（w）of the inertiaweight can be obtained byconnecting（wini，0）,（wend，0）,and（wk，2/（wini-wend））toform a triangle,whose area equals 1 exactly,as shown in Fig.1.Whenk=0,the triangle is a right triangle.

The probability distribution function of the inertia weight can be deduced from its probability density function.Fork=0, the probability distribution functionF0（w） is calculated with the following equation:

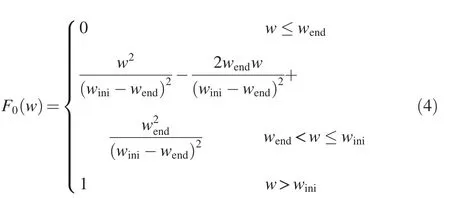
Fork＞0,the probability distribution function is as follows:

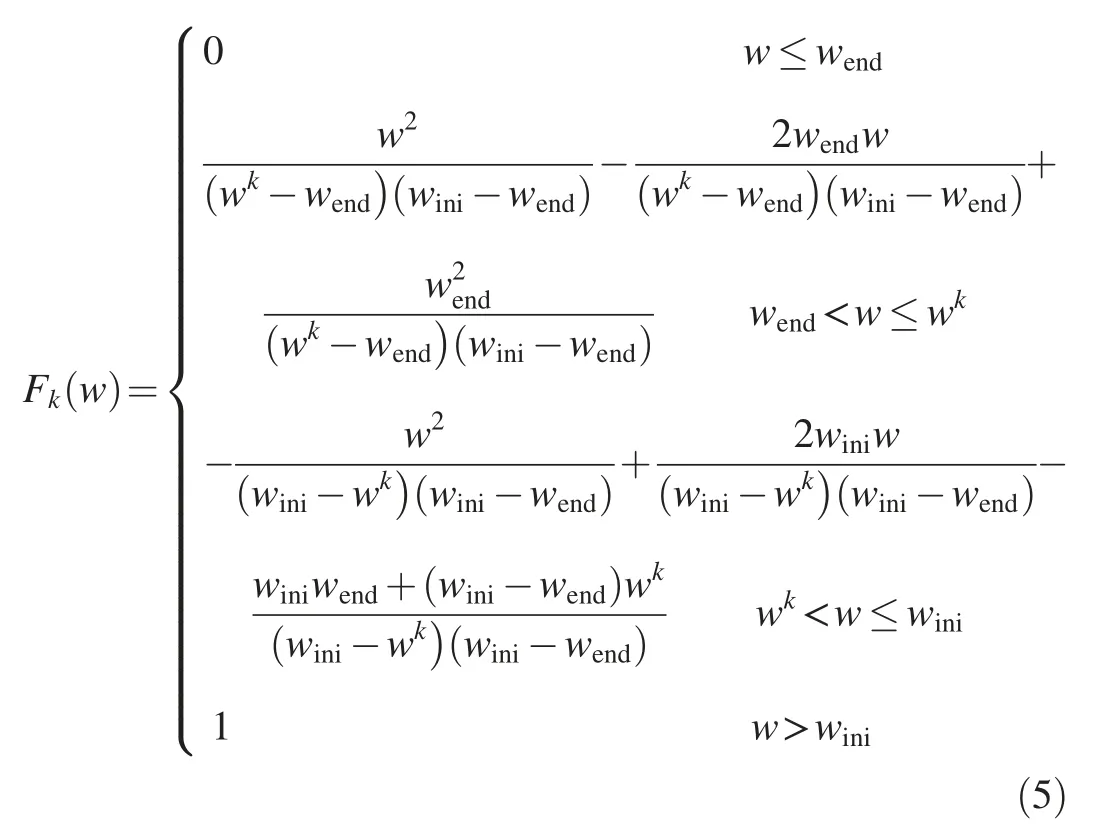
The inverse functions of the probability distribution functions fork=0 andk＞0 can be expressed respectively as follows:

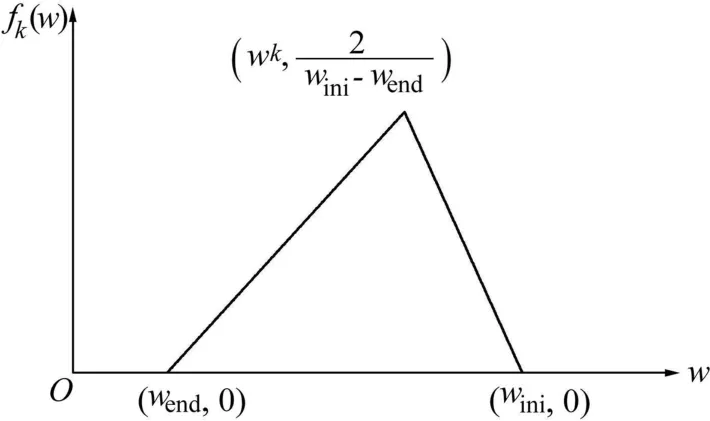
Fig. 1. Probability density of random inertia weights.

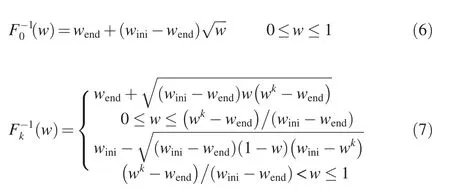
The inertia weight of each particle of the ARIW-PSO algorithm can be obtained with Eqs. (4) through (7). The calculation steps of the ARIW-PSO algorithm are as follows:

Step 1: Initialization of particles. A vector with the constraint of each component represents a particle, and the initial population is generated randomly. The initial position vector of theith particle in the swarm is assumed to be X0i,and the initial velocity vector is assumed to be V0i.

Step 2: Calculation of the fitness degree. For theith particle,using the given objective function,the fitness degreeRiof the current iteration result Xpiis calculated, and the fitness degreeR*of the particle swarm at the current iteration XGis also calculated.

Step 3: Updating the individual optimal solution. The fitness degreeRiof the current iteration result of the individual optimal solution Xpiis compared with that of the previous iteration result.IfRiof the current Xpiis higher than that of the previous result, the current Xpiis used to replace the previous result and to serve as the individual optimal solution, and the corresponding particle is updated.Otherwise,the pervious Xpiremains invariable.In this way,the individual optimal solution of each particle is obtained.

Step 4: Updating the global optimal solution. A similar method to that used to calculate the individual optimum is adopted.Comparing theR*value of the current iteration result of the global optimal solution XGwith that of the previous iteration result, ifR*of the current XGis higher than that of the previous result, then the current XGis used to replace the previous one to serve as the global optimal value. Otherwise,the previous XGremains invariable.

Step 5: Calculation of the random inertia weight. By generatingnrandom numbers uniformly distributed in the interval [0,1], the inertia weight of each particle is calculated with Eqs. (4) through (7).

Step 6: Modification of the particle swarm. The particle swarm is updated according to Eqs. (1) and (2). In order to improve the efficiency, the Gaussian disturbance can be used in the formula (Zhu et al., 2014).

Step 7:Termination criteria.Steps 2 through 6 are repeated until the pre-set iteration maximum is reached or the calculation accuracy is satisfied.

2.3. Test of ARIW-PSO algorithm with classical benchmark functions

Five classical nonlinear functions were used to test the performance of the ARIW-PSO algorithm, and results were compared with GA and other common improved PSO algorithms. The test functions for ann-dimensional variable X =（x1，x2，…，xn） are as follows:

(1) Quadric noise function:

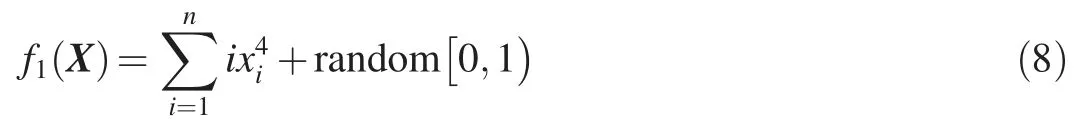
where -1.28 ＜xi＜ 1.28.

(2) Rastrigin function:

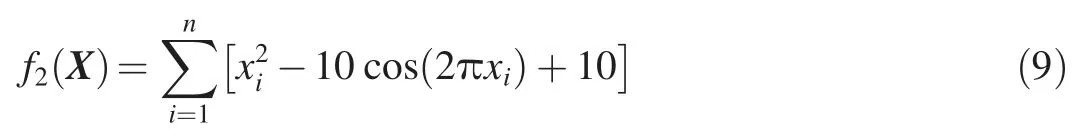
where -5.12 ＜xi＜ 5.12.

(3) Noncontinuous Rastrigin function:

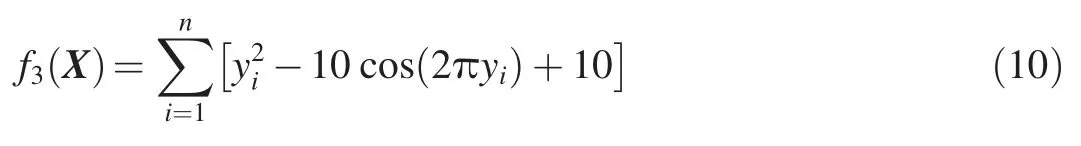
whereyi=xifor |xi|＜ 0.5, andyi=round（2xi）/2 for 0.5 ≤|xi|＜5.12.

(4) Ackley function:

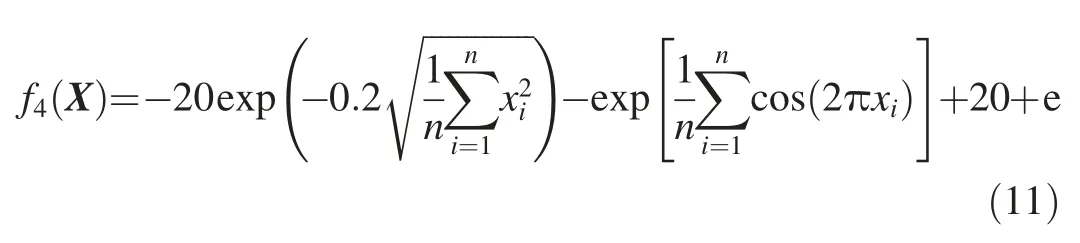
where -32 ＜xi＜ 32.

(5) Griewank function:

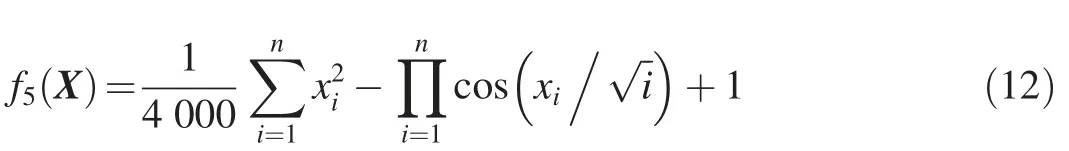
where -600 ＜xi＜ 600.

In this study, the theoretical optimum value of all five functions was zero,the dimension of X was set asn=30,the size of the swarm was set asN=30,and the particle velocity was limited to 10. Other parameters of the PSO algorithm were set as follows:c1=c2= 2.0,wini= 0.9,wend= 0.4,andkmax= 20 000.

According to the given parameters and Eqs.(4)through(7),the probability distribution functions, which were used to generate the random inertia weight, are evaluated as follows:

wherek= 1， 2，…，kmax.

In order to verify the performance of ARIW-PSO,we selected GA, the conventional PSO, and common improved PSO algorithms,including the self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients (HPSOTVAC), comprehensive learning particle swarm optimizer for global optimization of multi-modal function (CLPSO), and adaptive particle swarm optimization(APSO)(Zhu et al.,2014)for comparative experiments.To eliminate the random influence of the algorithms, each algorithm ran 30 times independently.The final averagevaluewas taken as the final optimization result.The average value and standard deviation were used to reflect the accuracy and stability of optimization, respectively. The test results of different algorithms are shown in Table 1.

According to the average value and standard deviation of 30 times of calculations,the ARIW-PSO algorithm is superior to other algorithms in overall search accuracy and stability.The ARIW-PSO algorithm performs well in thef2,f4, andf5functions. In particular, thef5function is a typical nonlinear multi-modal function, which has a wide search space. In general, it is difficult for a general optimization algorithm to deal with complex multi-modal problems,which may result in convergence to the local optimum, while the ARIW-PSO algorithm can find the global optimum well.

To illustrate the convergence effect of the proposed algorithm, the relationships between the number of iterations andthe logarithm of the corresponding fitness values for the five test functions were compared. The calculation results are shown in Fig. 2.

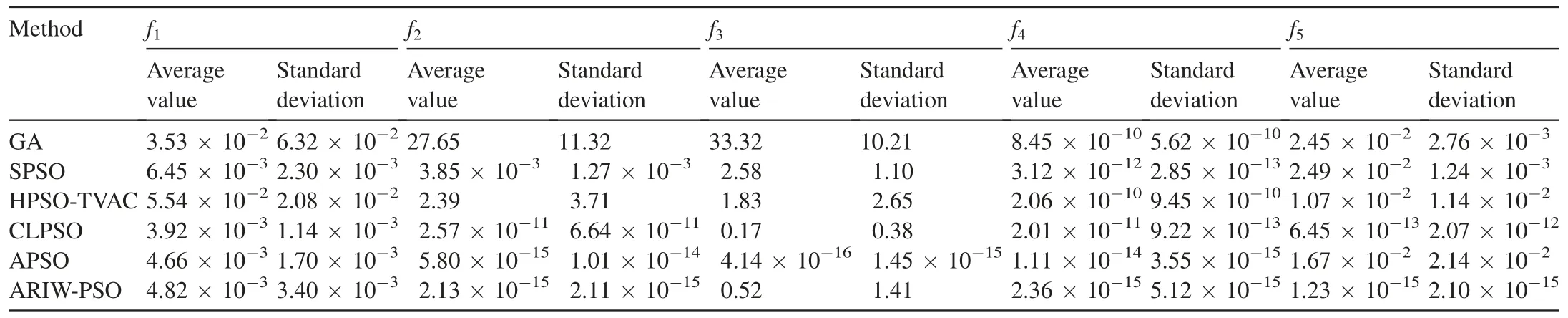
Table 1 Comparison of test results of different algorithms for different test functions.

According to the calculation results of Fig.2,the proposed ARIW-PSO algorithm enhanced the optimization ability and convergence speed through adaptive adjustment of the random inertia weight in this study.Compared with other algorithms,it has faster convergence speed, while other algorithms easily fall into local optima, which leads to a slower convergence speed or even stagnation.

3. Application of improved ARIW-PSO algorithm

3.1. Introduction of main reservoirs on Luanhe River

(1) The Panjiakou Reservoir is located on the midstream of the Luanhe River at the junction of Tangshan City and Chengde City in Hebei Province, China. It is the source of the Luanhe-Tianjin diversion project. It controls an area of 33 700 km2in the Luanhe River Basin, accounting for 75% of the whole basin, and controls more than 1/2 of the water quantity of the basin. The Panjiakou Reservoir's functions include flood control, water supply,hydroelectric power, and river ecological water supply. In these service objectives, power supply depends on the quantity of water, and power generation is dominated by the flow and water level of the reservoir during the process of water supply.

(2) The Daheiting Reservoir is located on the main stream of the Luanhe River, 30 km downstream of the Panjiakou Dam.The main function of the reservoir is to undertake water regulation of the Panjiakou Reservoir, raise water level, and supply water to Tianjin,Tangshan,and districts downstream of the Luanhe River.The Daheiting Reservoir controls an area of 35 300 km2of the river basin. The total storage capacity is 337 million m3, and the effective storage capacity is 224 million m3. The maximum water level, normal water level, and flood limit water level are 133.00 m, and the dead water level is 121.50 m.

(3) The Taolinkou Reservoir is located on the Qinglong River, a tributary of the Luanhe River in Qinhuangdao City,Hebei Province.It is a hydro-junction project for water supply,irrigation, flood control, and power generation. The reservoir controls a watershed area of 5 060 km2. The normal water level of the reservoir is 143.40 m,the flood limit water level is 143.40 m, the dead water level is 104.00 m, the total storage capacity is 859 million m3, and the utilizable reservoir capacity is 709 million m3.

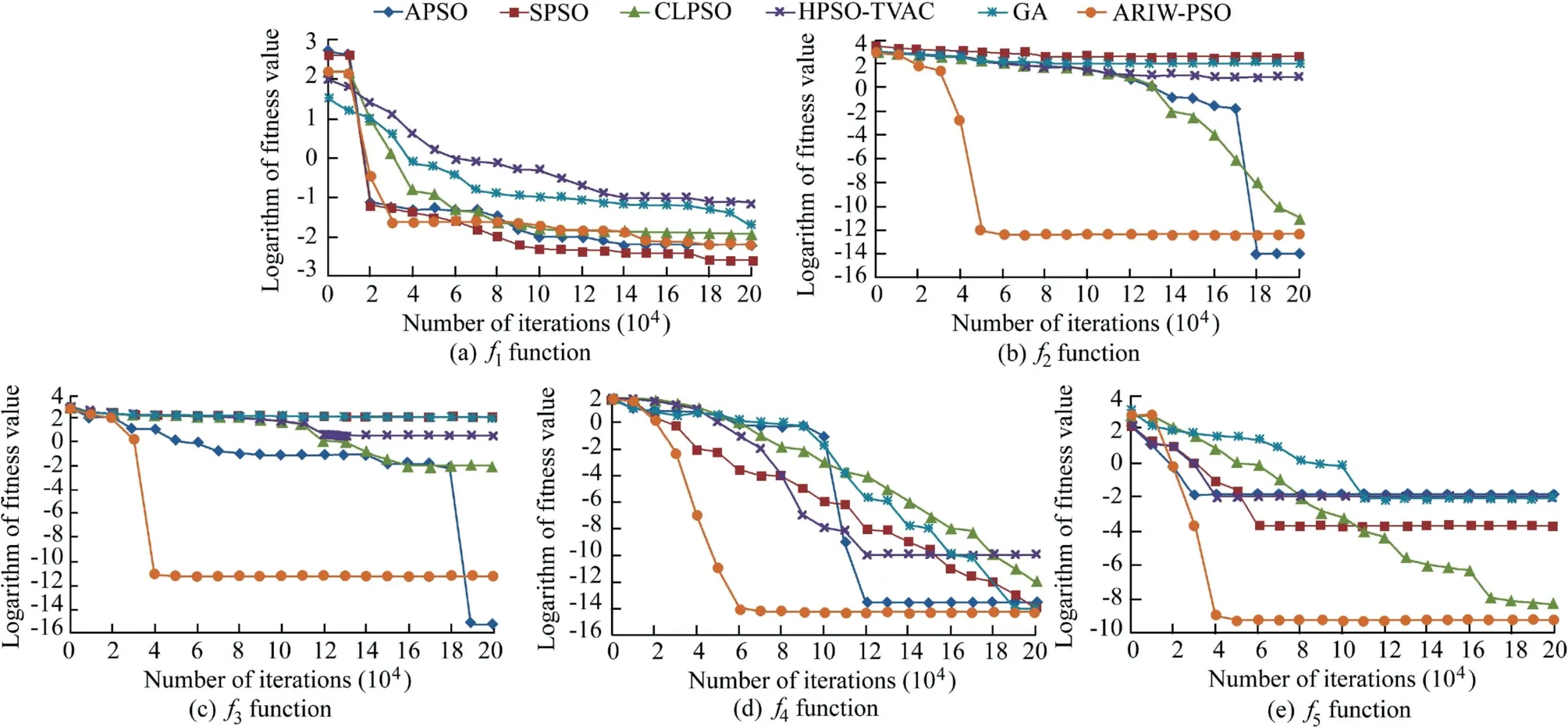
Fig. 2. Evolutionary processes of six algorithms for different functions.

3.2. Multi-objective optimal operation of Panjiakou Reservoir

In this study, the objectives were minimization of the deficits of both the domestic water supply and the ecological water supply. Ecological water supply is used to meet the water demand of river ecosystems.Because of the limited total storage,the two objectives are contradictory.In order to solve this problem,the weighted method was adopted.By assigning a weight to each objective, the multi-objective problem was transformed into a single-objective problem. The objective function is as follows:

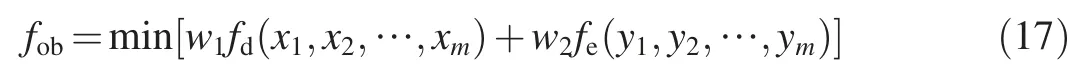
wherefd（x1，x2，…，xm） is the objective function of domestic water supply,which reflects the comprehensive extent of water deficits for domestic water supply, and is calculated as follows:

wherexiis the actual domestic water supply of each calculation period (108m3);piis the domestic water demand of each period (108m3);mis the number of calculation periods,andm= 18 in this study. From July to September, the length of the calculation period was 10 days, and the rest of the calculation periods were one month.

fe（y1，y2，…，ym） is the objective function of ecological water supply, reflecting the extent of the overall deficit of the ecological water supply, and is evaluated as follows:

whereyiis the actual water released to rivers in each calculation period (108m3), andsiis the ecological water demand of rivers in each period (108m3).

w1andw2are the weight coefficients, representing the importance of the objectives for the decision maker. Target weights can be calculated with the analytic hierarchy process method, according to the opinions of experts.

This procedure was subject to the following constraints:

(1) Water level of the reservoir:

whereZiis the water level of theith calculation period (m),Ziminis the allowable lowest water level (m), andZimaxis the allowable highest water level (m).

(2) Discharge limits:

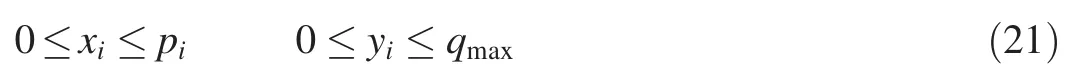
whereqmaxis the discharge capacity of each period (108m3).

(3) Mass balance equation:

whereVtis the reservoir storage at the end of periodt(108m3),is the average inflow during periodt(m3/s),is the average release during periodt(m3/s),and Δtis the length of the calculation period.

(4) Rules of flood control:

Reservoir operation in the flood season obeys the rules of flood control operation.During the main flood season(July 21 to August 15), when the water level of the reservoir is below 216 m, the main task is to store water to meet the water demand downstream; when the water level of the reservoir is between 216 and 222 m, the flood discharge is less than 10 000 m3/s;when the water level is between 222 and 225 m,the discharge of the reservoir is less than 28 000 m3/s; when the water level exceeds 225 m,the flood discharge facilities of the reservoir are all open.In the later flood season(August 16 to September 30),the flood limit water level can gradually rise to 222 m, and the maximum water level of the reservoir can reach 225 m from September 1 to September 30.

According to the relevant research results, the monthly average domestic water demand of the Panjiakou Reservoir and the monthly ecological water demand of the Luanhe River are shown in Table 2 and Table 3, respectively.

According to the historical data of the Panjiakou Reservoir,the low-flow year from July 1981 to June 1982 was selected as an example, and the multi-objective optimal operation model for the typical year was solved with the ARIW-PSO algorithm.The inflows of the Panjiakou Reservoir in the low-flow year are shown in Table 4.

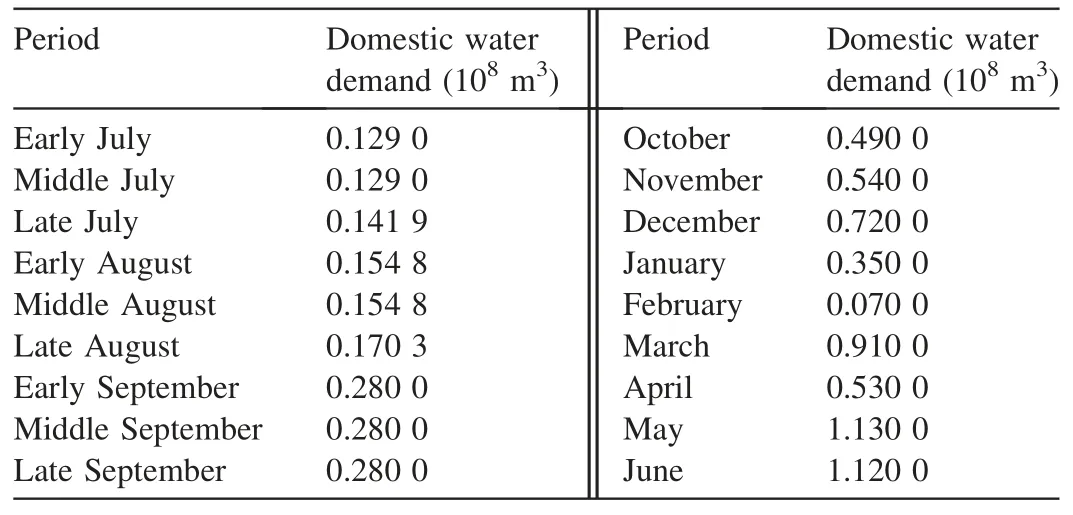
Table 2 Domestic water demand of Panjiakou Reservoir.

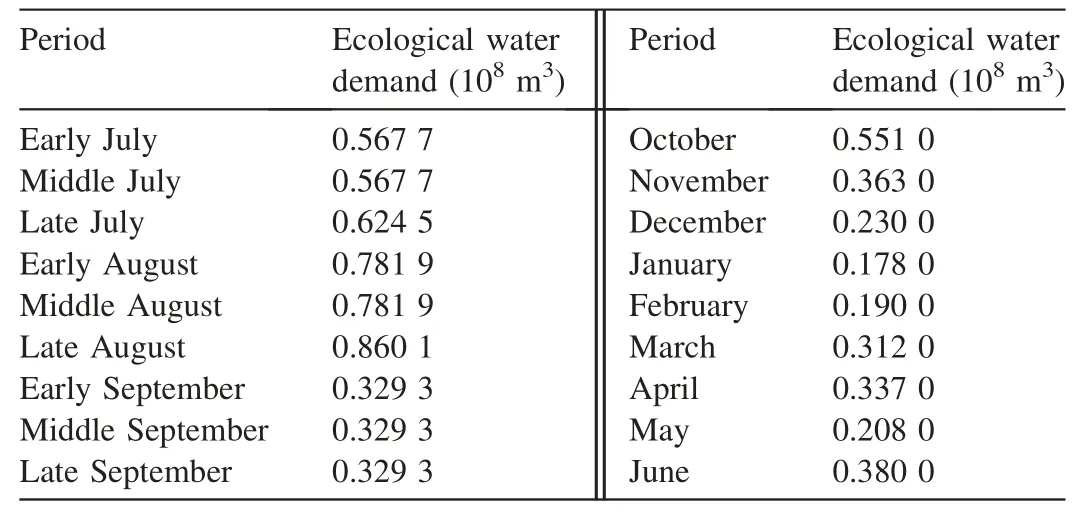
Table 3 Ecological water demand of Luanhe River.

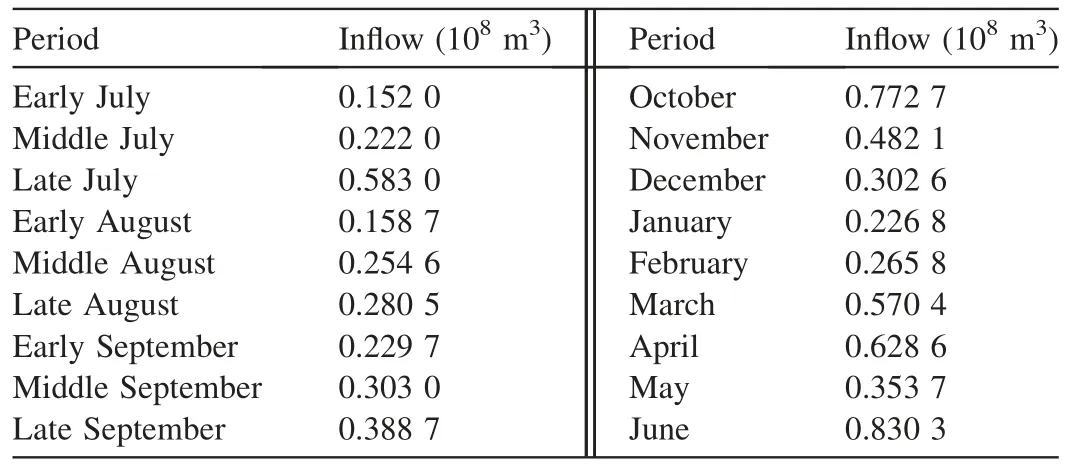
Table 4 Inflows of Panjiakou Reservoir in low-flow year.

The initial water level was 164.48 m, which is the allowable lowest water level during the regulation period. With the weights of the two objects set to be 0.9 and 0.1, respectively,using the ARIW-PSO algorithm, the regulation results of the Panjiakou Reservoir are shown in Table 5.

In the low-flow year, neither the domestic water demand nor the ecological water demand can be met.Through optimal dispatch with the ARIW-PSO algorithm, the extent of the deficits of domestic water supply and ecological water supply gets flattened, and the degree of water deficit is reduced.According to the calculation result of the optimal value of the objective function, the comprehensive water shortage of domestic water supply and ecological water supply for the lowflow year was 0.970 6 billion m3after optimal dispatch.Table 5 shows that the maximum ecological water deficit occurred in early August, with a value of 78.19 million m3.The largest domestic water deficit occurred in May, with a value of 39.07 million m3. In these two stages, the corresponding water demand was large,while the water supply was insufficient. For validation of the ARIW-PSO algorithm, GA and conventional PSO were used to calculate the optimal values of the objective function in this study, and the optimal values were 1.876 billion m3and 1.399 billion m3, respectively. The comprehensive water shortage degree calculated with ARIW-PSO is the lowest, making the impact of water shortage minimal.

3.3. Multi-objective flood control operation of reservoir group on Luanhe River

Fig. 3 shows the reservoir group on the Luanhe River selected in this study.Assuming that the inflow process of the Panjiakou Reservoir isQ1，t, the flow from the Panjiakou Reservoir to the Daheiting Reservoir isQ2，t,the flow from the Daheiting Reservoir to the lower reaches of the Luanhe River isQ3，t, the flow from the Taolinkou Reservoir isQ4，t, and the flow from the Taolinkou Reservoir to the lower reaches of the Luanhe River isQ5，t.The flood process in the lower reaches of the Luanhe River isQt, withTypical water inflow processes of the reservoirs were selected for case study,as shown in Fig. 4.

The multi-objective optimal operation was to minimize the water level of each reservoir and the peak flow in the lower reaches of the Luanhe River. In order to facilitate calculation,each objective was normalized. The integrated objective function is as follows:

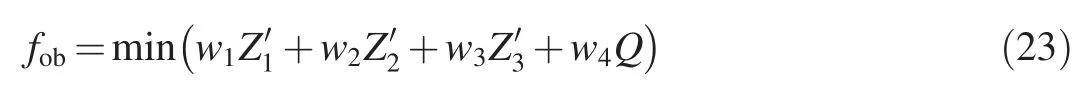
The variables were normalized through being divided by their upper limit values. For the Panjiakou Reservoir,Daheiting Reservoir,and Taolinkou Reservoir,the upper limitsof the water level were 227.00 m, 134.00 m, and 144.32 m,respectively. The upper limit of the peak flow in the lower reaches of the Luanhe River was set as 15 000 m3/s according to historical data. The main constraints were the water level,flow limitation, and water balance of each reservoir. The weights were determined by the analytic hierarchy process,and specified to be 0.2,0.3,0.2,and 0.3 for the water levels of the Panjiakou Reservoir, Daheiting Reservoir, and Taolinkou Reservoir, and the peak discharge of the lower reaches of the Luanhe River, respectively. Then, the ARIW-PSO algorithm was applied to flood control dispatch of the reservoir group for the typical flood process.

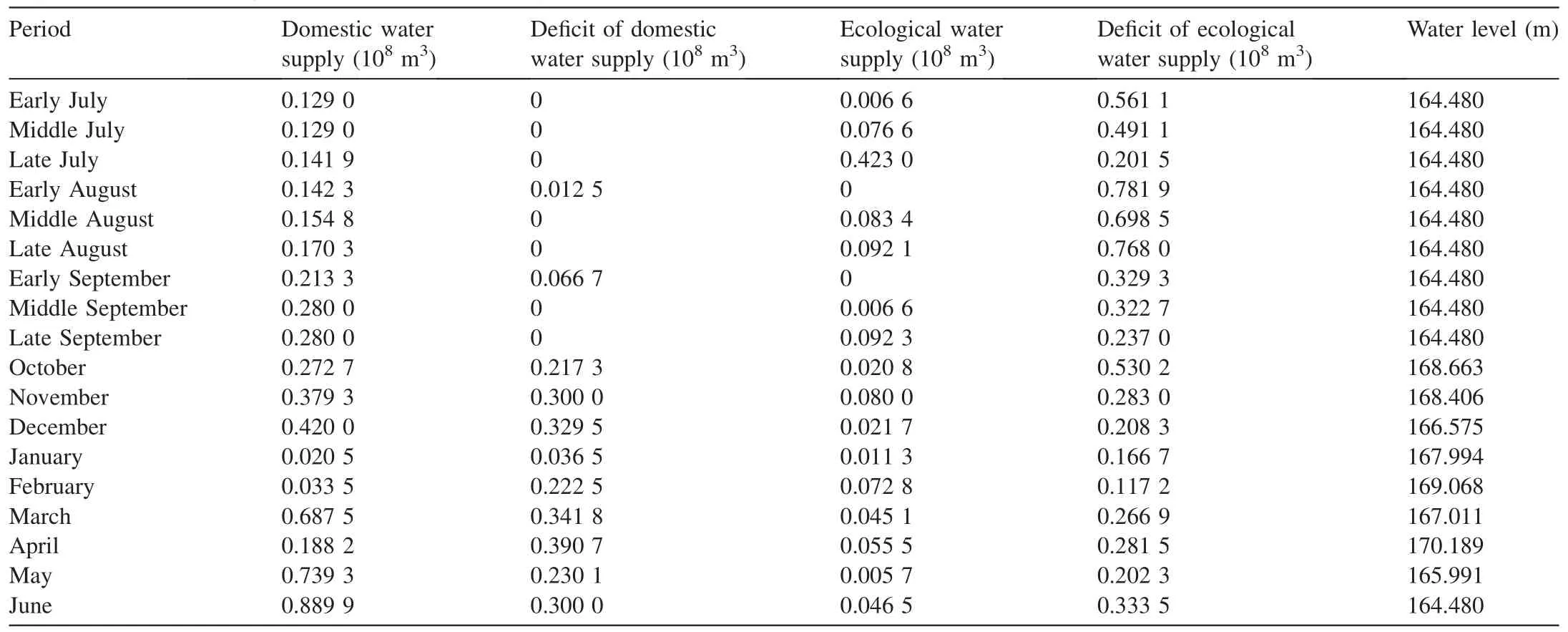
Table 5 Regulation results of Panjiakou Reservoir in low-flow year.

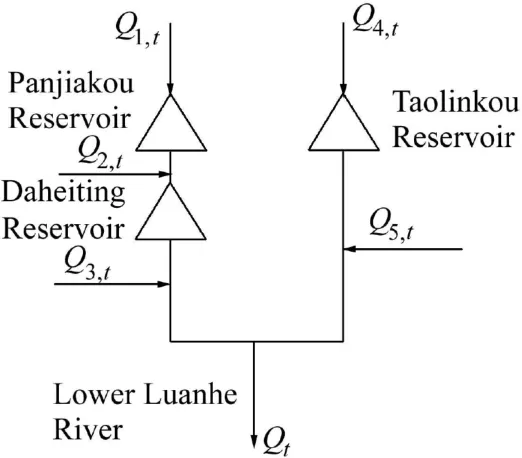
Fig. 3. Diagram of reservoir group on Luanhe River.

Fig. 4. Water inflow processes.

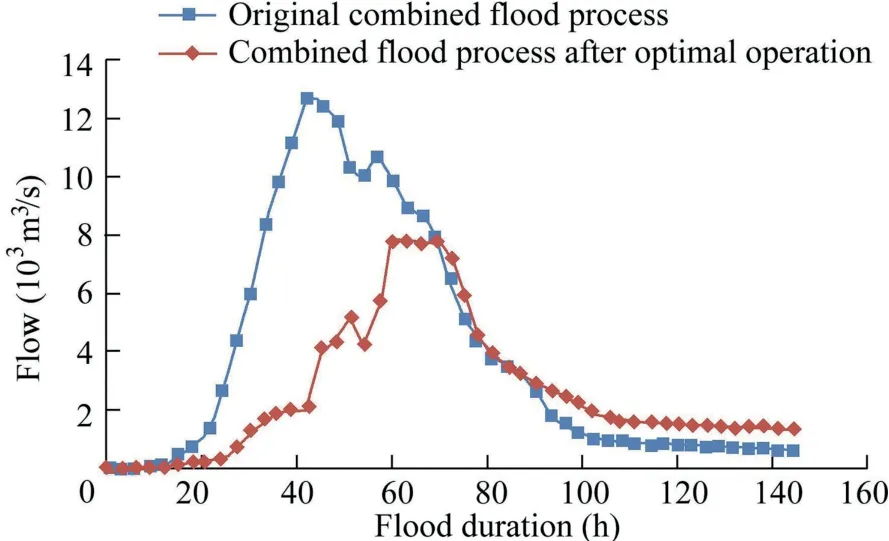
Fig. 5. Flood processes before and after optimization.

Fig.5 shows that without adoption of multi-objective flood control operation of the reservoir group, the combined flood process in the lower reaches of the Luanhe River has a high flood peak, with the value reaching 12 694 m3/s. After multiobjective optimal operation of the reservoir group by the ARIW-PSO algorithm,the flood peak is greatly reduced, with the value decreased by 7 823 m3/s,and the highest water levels of the Panjiakou Reservoir, Daheiting Reservoir, and Taolinkou Reservoir were 223.93 m, 133.44 m, and 143.51 m,respectively. The calculated result of the objective function(Eq.(23))was 0.851 4,while the calculated results of GA and the conventional PSO were 0.965 1 and 0.887 6, respectively.

4. Conclusions

The main contributions of this study can be summarized as follows:

(1) ARIW was combined with the conventional PSO algorithm in this study to improve the performance of the PSO algorithm.Based on the triangular probability density function,the inertia weight is randomly generated, and the probability distribution function is automatically adjusted with the evolution. In the initial evolution stage, the inertia weight is generally larger, which is suitable for global optimization. With the progress of evolution, the inertia weight decreases gradually,which is beneficial to local searches. The test of the proposed ARIW-PSO algorithm with typical benchmark functions shows that the ARIW-PSO algorithm is superior to GA, the conventional PSO algorithm, and other common improved PSO algorithms in overall search accuracy and stability.

(2) The application of the ARIW-PSO algorithm to the multi-objective optimal dispatch of the Panjiakou Reservoir in China shows that the ARIW-PSO algorithm is more efficient than the conventional PSO algorithm and GA.Using the ARIW-PSO algorithm, the water deficit for water supply tends to be flattened, alleviating the loss caused by water shortage. The maximum ecological water deficit occurred in early August, with a value of 78.19 million m3. The largest domestic water deficit occurred in May,with a value of 39.07 million m3.

(3) The multi-objective optimal operation of the reservoir group on the Luanhe River, including the Panjiakou Reservoir, Daheiting Reservoir, and Taolinkou Reservoir, was studied using the ARIW-PSO algorithm, and the complex multi-dimensional regulation model was successfully solved with the ARIW-PSO algorithm. Through multi-objective optimal operation of the reservoir group, the peak flow of the lower reaches of the Luanhe River was reduced from 12 694 m3/s to 7 823 m3/s.The results of this study show that the PSO algorithm improved through its combination with ARIW can be effectively used to solve real-time optimization problems.

Declaration of competing interest

The authors declare no conflicts of interest.