小水线面三体船耐波性数值模拟

张明霞，卢鹏程，王志豪

大连理工大学船舶工程学院，辽宁大连116024

0 引 言

三体船作为一种新型高性能船舶，引起了人们的广泛关注［1-2］。该船由1 个主体和2 个小侧体构成，兴波阻力较小，2 个侧体不仅可以增加稳性，还可以增加横摇阻尼，具备良好的耐波性能。与单体船相比，三体船具有航速高、适航性好、易于大型化、便于模块化建造的优点［3］。相比常规船舶，普通双体船、穿浪双体船等的阻力性能和横稳性虽较好，但同时也具有结构重量较大、静水阻力较大、纵向稳定性较差、吃水较深、对装载重量敏感等缺点［4］。小水线面双体船具有较好的耐波性，能降低阻力，但同时也失去了普通多体船在舱容和甲板面积方面的优势。而小水线面三体船（trimaran small waterplane area center hull，TriSWACH）既有小水线面船耐波性良好、高速航行时阻力性能优的特点，又有与普通三体船相同的甲板面积大、布置性能好、横向与纵向稳定性优良的优点［5］。小水线面三体船由1 个水线面型主体和2 个侧体构成，在水面附近为薄立柱，下面布置有潜体。与长度相当的细长型三体船相比，小水线面三体船拥有更大的排水量，能提供更多有效载荷，应用前景可观［6-9］。

自20 世纪70 年代开始，前苏联就针对三体船的阻力性能进行了理论研究，英国、美国、澳大利亚等国家开展了针对三体船水动力性能和静力学性能等的研究。Ackers 等［10］针对三体船进行了大量的模型试验，得出侧体的纵向、横向位置以及对称性是影响三体船阻力性能主要因素的结论。Hebblewhite 等［11］通过船舶模型试验，研究了三体船侧体位置对三体船纵摇与垂荡运动的影响，结果表明在迎浪环境下，侧体纵向位置会显著影响垂荡和纵摇性能。在国内，李培勇等［12-13］针对三体船的横摇性能进行了试验和理论研究；刘宇辰等［14］针对三体船的横摇运动做了系列研究；张文鹏等［1］和贾敬蓓等［15-16］基于大连理工大学的船模拖曳水池进行试验，研究了三体船的阻力和耐波性能。对于相近船型小水线面三体船，顾敏童等［6］进行了模型试验，研究了潜体剖面为椭圆形的小水线面三体船的阻力特征，并与细长型三体船进行了对比，结果显示高航速时小水线面三体船的阻力性能更优。由于试验费用高昂，经验公式估算方法又存在一定的局限性，故采用计算流体动力学（CFD）方法分析船舶水动力性能越来越普遍。Bingham 等［17］研究了三体船在波浪中的运动及波浪载荷，证明三维移动脉动源方法适于研究 三 体 船 的 运 动。Elcin［18］和 卢 晓 平 等［19］采 用Rankine 源面元法，分析了侧体位置对三体船运动性能的影响。郦云等［20］针对细长型三体船设计了15 种侧体布局方案并进行数值模拟，分析了侧体位置对兴波阻力的影响。Duan 等［21］和Wei等［22］采用2.5D 法对三体船的阻力和耐波性进行了预测。

在小水线面三体船研究领域，目前国内还主要停留在阻力性能、结构水动力性能方面；在耐波性能方面，也未涉及侧体位置对其的影响。相比普通三体船，小水线面三体船的水线面极大地减小了，使得普通三体船型的设计经验不完全适用于小水线面三体船设计。郭俊伟［23］针对小水线面三体船分析了零航速横摇运动对横向波浪设计载荷的影响，但其3 个浮体主要用于在恶劣海况下开采石油，并不适于海上高速航行。尹木兰［24］、董哲［25］和刘嵩［26］对复合型小水线面三体船的阻力与耐波性能进行数值模拟分析，得出了小水线面三体船的耐波性随航速变化的规律，但其主要考虑的是艏鳍等问题，并未考虑侧体位置变化带来的影响。张明霞等［27-28］分析了小水线面三体船的阻力性能，并与细长型三体船就剩余阻力进行了对比，可为本文研究提供数值模拟试验基础。

有关小水线面三体船水动力性能研究方法，文献［27］证明了Spalart-Allmaras 湍流模型适用于小水线面三体船的阻力性能计算，但未证明该模型及网格设置方法是否适用于耐波性计算。

本文将利用STAR-CCM+平台，基于黏性理论，首先对三体船的垂荡与纵摇响应幅值进行计算，然后与文献［16］中的试验结果进行比较，验证该方法的有效性和可靠性，并在此基础上，研究小水线面三体船与相当船长普通三体船在耐波性能方面的差异，以及不同侧体位置对小水线面三体船耐波性能的影响。

1 计算模型与侧体布局方案

1.1 计算模型

基于文献［16］中三体船模型，船长、船宽、排水量均保持不变，将三体船模型型线转化为小水线面三体船模型［27］，船模横剖面如图1 和图2 所示。三体船模型及小水线面三体船模型主尺度参数分别如表1 和表2 所示，实船与模型的缩尺比为25。

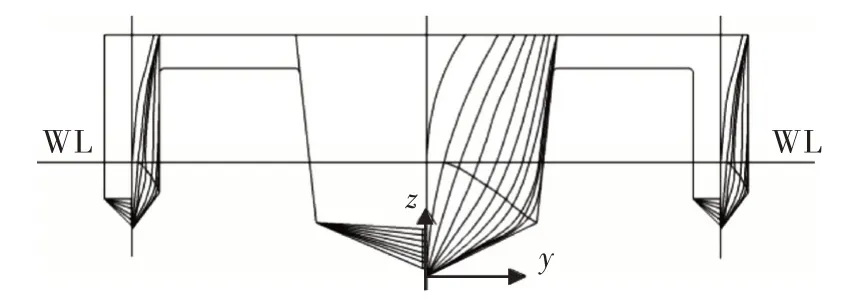
图1 三体船模型横剖面型线示意图［16］Fig.1 Schematic diagram of cross-section lines of trimaran

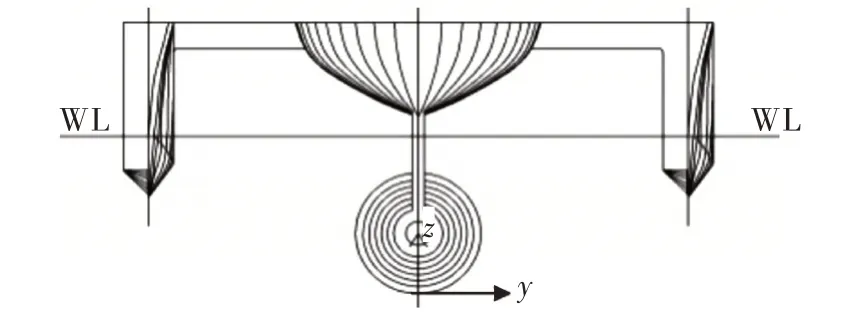
图2 小水线面三体船模型横剖面型线示意图［27］Fig.2 Schematic diagram of cross-section lines of TriSWACH

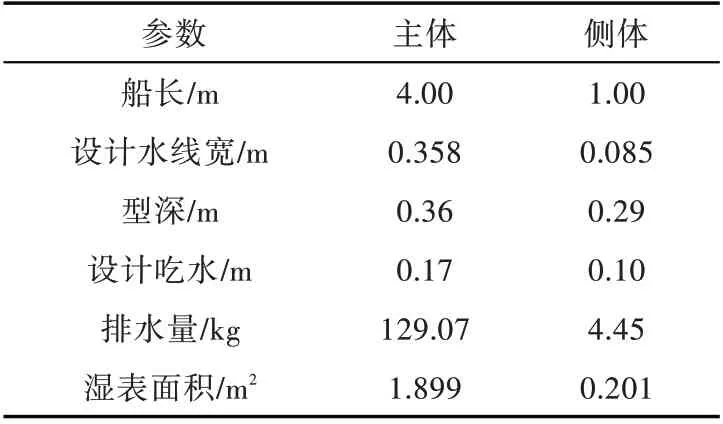
表1 三体船模型主尺度参数［16］Table 1 Main dimensions of trimaran

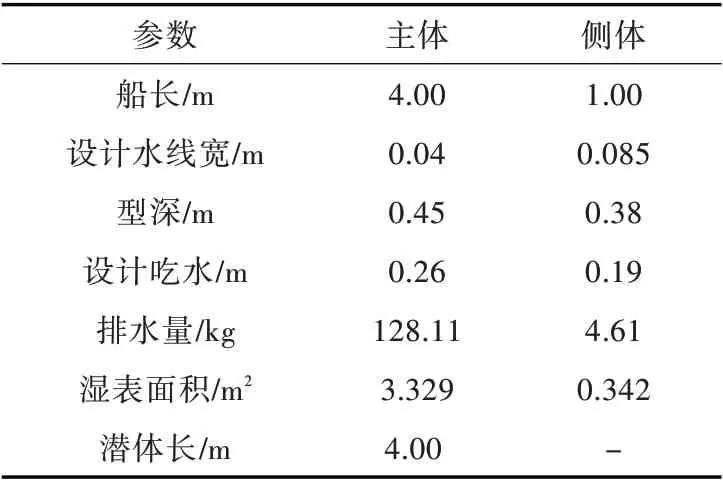
表2 小水线面三体船模型主尺度参数［27］Table 2 Main dimensions of the TriSWACH

三体船的船体坐标系如图3 所示。图中，x轴沿主船体船长L 方向，指向主体艏部为正，y 轴沿船宽方向，指向左舷为正；侧体中心线至主体中心线的距离为a ，侧体船舯至主体船舯的纵向距离为b，当侧体在主体船舯之前时b 为正值，否则为负。图4 所示为小水线面三体船的三维视图。

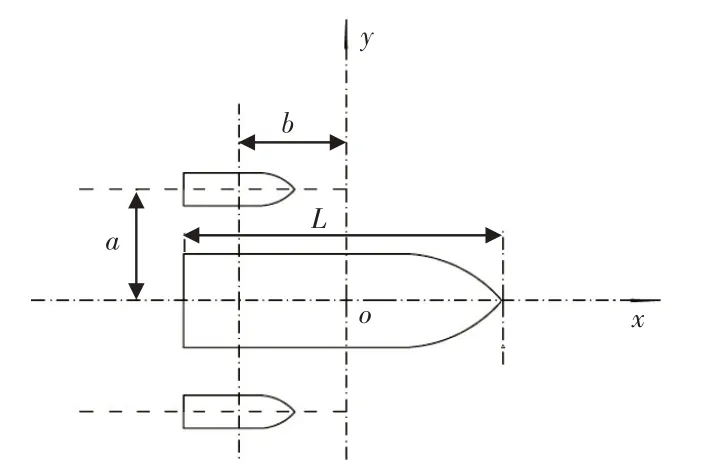
图3 船体坐标系Fig.3 Coordinate system of ship hull

图4 小水线面三体船三维视图Fig.4 The 3D view of TriSWACH

1.2 侧体布局方案

为充分考虑侧体纵、横向位置的影响，选择3 种纵向位置、2 种横向位置，形成4 种侧体位置布局方案，如表3 所示。

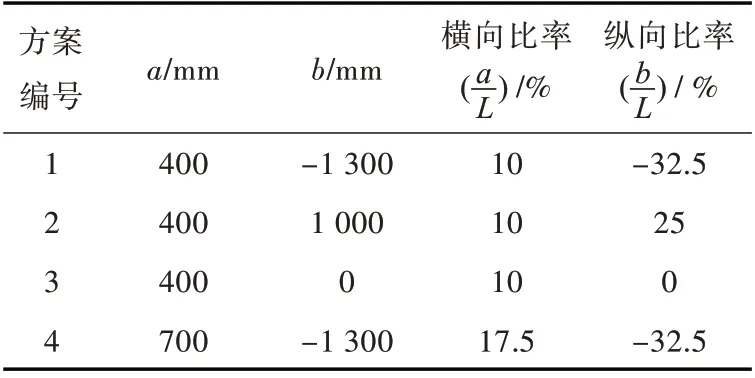
表3 小水线面三体船模侧体位置方案Table 3 The schemes of TriSWACH's side position

2 建模及数值方法

2.1 流域设置及网格划分

为模拟水池试验的流场环境，在STAR-CCM+软件中建立了数值模拟拖曳水池。针对小水线面三体船这种对称船型，取左侧船体进行计算，可以得到与整体一样的计算结果，并且可以减少约一半的网格，大幅度减少计算量。如图5 所示，计算流域入口取主体艏部向上游延伸3L 处，出口取艉部向下游延伸至5L 处；区域右侧边界为对称面，左侧边界面向左舷方向延伸1L；计算流域高度为2L，流域上边界取设计水线面向上约0.75L 处。计算流域边界条件设置为速度进口、压力出口、对称面和壁面。

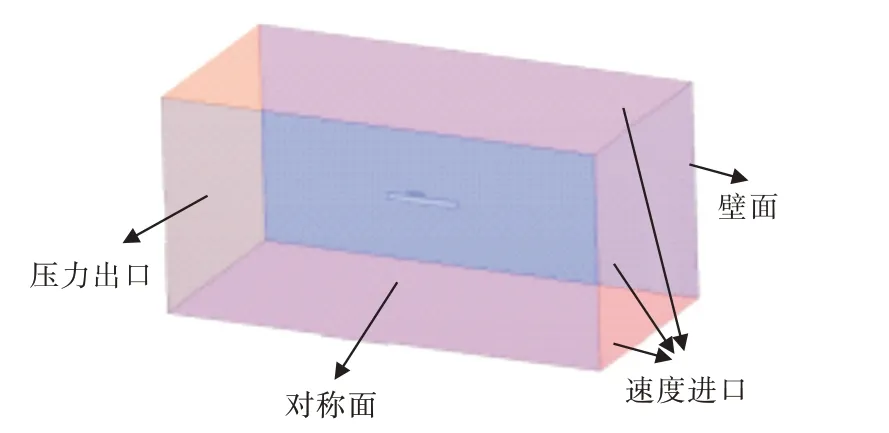
图5 流域设置Fig.5 Fluid region setting

采用STAR-CCM+平台自动划分流域网格，在设置网格相关参数时，对船艏、船艉等曲率变化较大的区域和水线面处网格进行加密处理，然后由船体以一定的梯度外推，形成重叠网格，再以开尔文波系形状、尾流场分别设置梯度外推的网格。网格参数设置如表4 所示，网格划分如图6 所示。

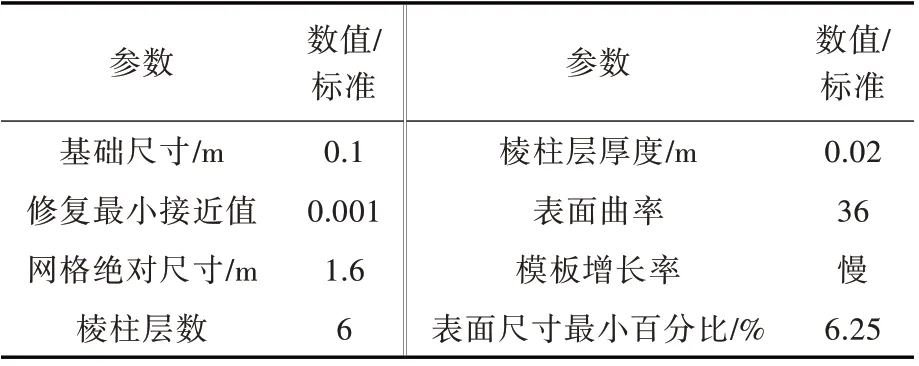
表4 网格参数设置Table 4 Setting of mesh parameters

图6 流域网格划分Fig.6 Mesh generation of fluid region

采用动态流体固体相互作用模块（dynamic fluid body interaction，DFBI）运动进行模拟，放开纵摇、升沉这2 个自由度，开始时间为1 s，缓冲时间5 s。

2.2 控制方程和湍流模型

三体船黏性流场的连续方程和动量方程［29-32］分别如下：

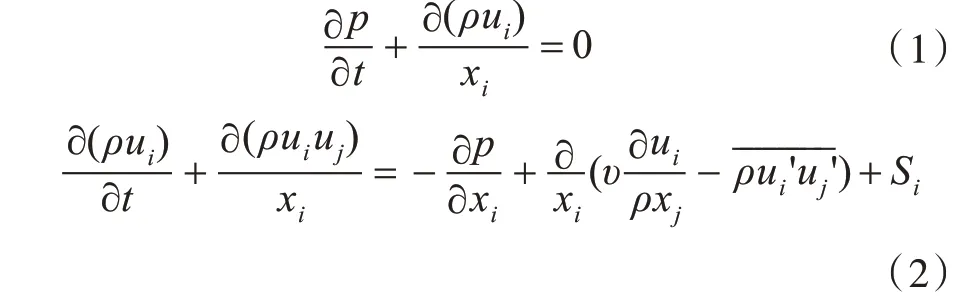
式中：ui，uj为速度分量时均值（i ，j =1，2，3）；ρ 为流体密度；p 为压力时均值；υ 为流体运动黏性系数；'为雷诺应力项，xi，xj为笛卡尔坐标系中的坐标分量；t 为时间；Si为广义源项。

方程采用Spalart-Allmaras 湍流模型封闭RANS 方程，该湍流模型具有较好的稳定性和计算精度标准，适用于尾迹流动计算、混合层计算、射流计算，以及受壁面限制的流动计算和自由剪切流计算，具有近壁区计算的优点［27］。

在空气与水的交界面会产生船行波，这对船舶运动，尤其是高速船舶的运动影响较大。三体船作为排水型船舶，需要考虑自由表面的问题，数值方法可选用流体体积（volume of fluid，VOF）法，用于捕捉自由液面。VOF 法是通过定义一个流域体积函数F，来定义划分的每个网格单元的状态。F 等于一个单元内流体体积与该单元体积之比。若F=1，说明该单元全部为指定相流体所占据；若F=0，表明该单元为无指定相流体单元；若0＜F＜1，则可认为该单元内含有自由表面［33］。流域体积函数F 的公式为

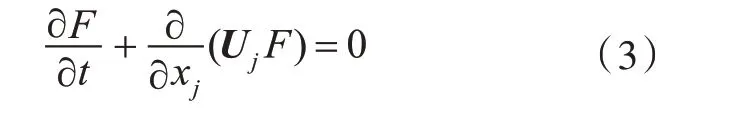
式中，Uj为自由流速度矢量。

2.3 波浪模拟方法

采用一阶规则波浪，并使用定义初始边界的方法造波，波面升高函数表达式为

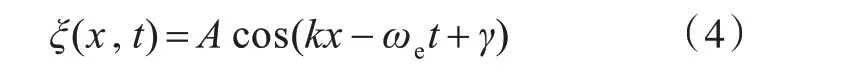
式中：ξ 为某一点在某一时刻的纵向位置；A 为波幅；k 为波数；ωe为遭遇频率；γ 为相位，可以选为0～2π之间的任意值。船舶以一定的航速和遭遇浪向航行时，实际作用于船体的波浪频率已经不是波浪本身的自然频率ω，而是遭遇频率ωe，故转化公式如下：

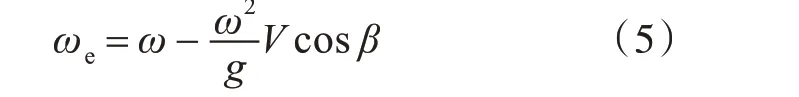
式中：g 为重力加速度，m/s2；V 为船模速度，m/s；β 为遭遇浪向，在试验中取-1，即迎浪，其浪向示意图如图7 所示。

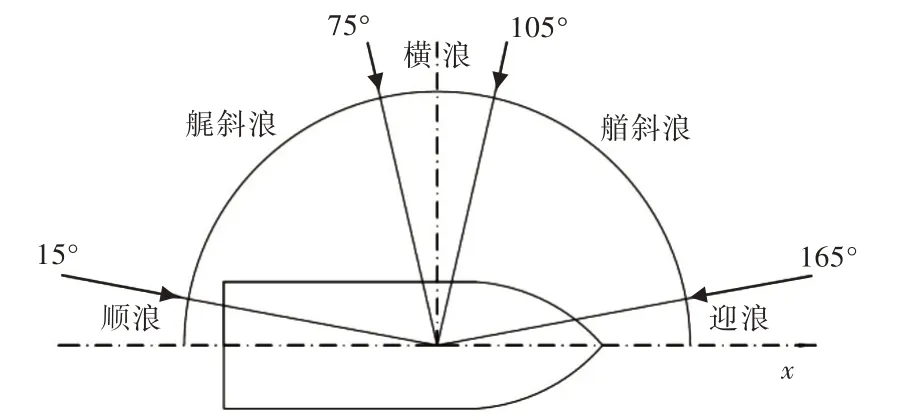
图7 遭遇浪向示意图Fig.7 Schematic diagram of encountered wave direction

2.4 频率响应幅值函数

计算中引入了放大因数运动响应幅值算子（RAO）［16］，并对垂荡与纵摇响应幅值进行无量纲化处理，以便于衡量船体在规则波中的运动响应幅值。试验以文献［16］中放大处理后的遭遇频率系数作为自变量。处理后的频率响应幅值函数如下。

垂荡放大因数：

纵摇放大因数：

遭遇频率放大因数：

以上式中：ZA为垂荡幅值；A0为规则波波幅，m；θA为纵摇幅值；α0=kA0= 2πA0/λ，为规则波表面波倾，其中λ 为波长，m。

3 模型验证及结果分析

3.1 数值方法验证

为检验STAR-CCM+平台使用Spalart-Allmaras湍流模型计算小水线面三体船耐波性的敏感性和准确性，首先按照文献［16］的标准建立三体船模型并设置验证方案，然后在STAR-CCM+平台中设置与小水线面三体船相同的计算域条件，以及与模型试验相同的迎浪条件，并对结果进行对比分析。小水线面三体船作为一种高速船舶，在横浪、艉斜浪时耐波性能较好［33］。而迎浪航行状态是一种典型的状态，下文也将采用迎浪条件进行计算分析。

验证方案设置了2 种弗劳德数（Fr=0.234，0.494），对a=400 mm，b=0 mm 侧体构型的小水线面三体船纵摇、垂荡模拟值与试验值进行了对比，结果如图8～图11 所示。

由图8～图11 可以发现，采用数值模拟方法时，垂荡响应幅值的最大计算误差为9.23%，纵摇响应幅值的最大计算误差为9.29%，且数值计算与试验得到的曲线吻合度较好。因此，可以应用上述数值方法进行小水线面三体船的耐波性计算与分析。

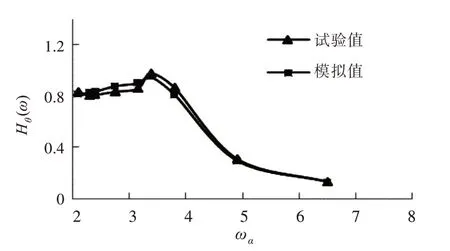
图8 Fr=0.234 时纵摇放大因数曲线Fig.8 Curves of pitch RAO at Fr=0.234

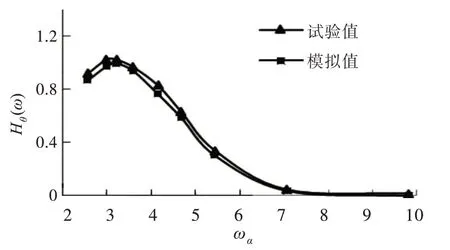
图9 Fr=0.494 时纵摇放大因数曲线Fig.9 Curves of pitch RAO at Fr=0.494

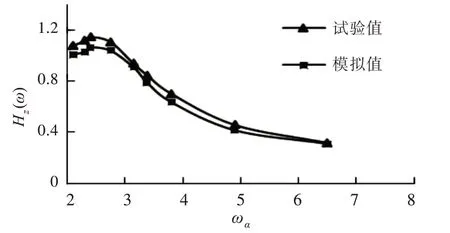
图10 Fr=0.234 时垂荡放大因数曲线Fig.10 Curves of heave RAO at Fr=0.234

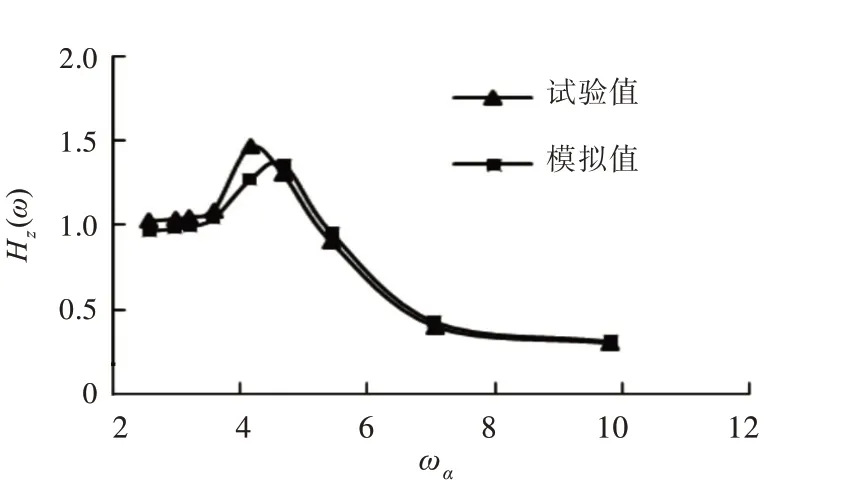
图11 Fr=0.494 时垂荡放大因数曲线Fig.11 Curves of heave RAO at Fr=0.494

3.2 小水线面三体船与普通三体船耐波性能对比

在已验证使用STAR-CCM+平台进行数值模拟的可靠性基础上，以相当船长的小水线面三体船和普通三体船（a=400 mm，b=0 mm）在Fr=0.234，0.494 和0.701，波幅A=20 mm 的情况下进行纵摇与垂荡响应幅值的对比。普能三体船采用水池试验值［16］，小水线面三体船采用STAR-CCM+模拟值。对比2 种船型的纵摇与垂荡放大因数，结果如图12～图17 所示。

由图12～图13 可以看出，当Fr=0.234 时，小水线面三体船的纵摇和垂荡响应幅值整体上小于普通三体船，且峰值分别比普通三体船小7.41%和13.80%。在低航速下，小水线面三体船相比普通三体船耐波性更好（垂荡及纵摇幅值越低，表明该船耐波性越好）。

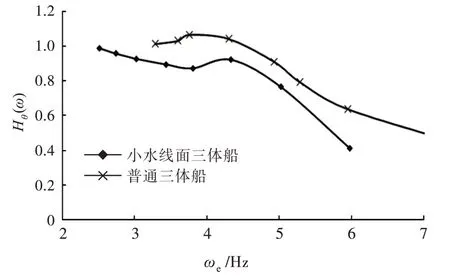
图12 Fr=0.234 时纵摇放大因数对比Fig.12 Comparison of pitch RAO at Fr=0.234

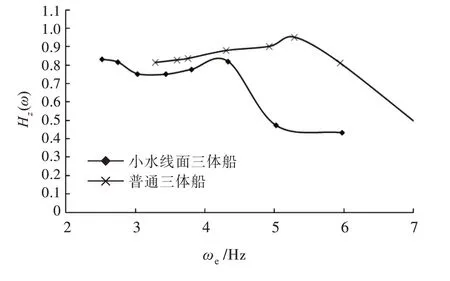
图13 Fr=0.234 时垂荡放大因数对比Fig.13 Comparison of heave RAO at Fr=0.234

由图14 可看出，当Fr =0.494，遭遇频率ωe＜6.5 Hz 时，小水线面三体船的纵摇响应幅值大于普通三体船，峰值比普通三体船高8.09%；当遭遇频率ωe＞6.5 Hz 时，小水线面三体船的纵摇响应幅值小于普通三体船。由图15 可以看出，在遭遇频率ωe在5～6 Hz 之间时，有部分区间小水线面三体船的垂荡响应幅值略大于普通三体船，其他区间均小于普通三体船；小水线面三体船垂荡响应幅值的峰值大幅低于普通三体船，约低23.9%。在中航速下，小水线面三体船的垂荡性能优于普通三体船，但纵摇性能无明显优势，甚至稍差于普通三体船。

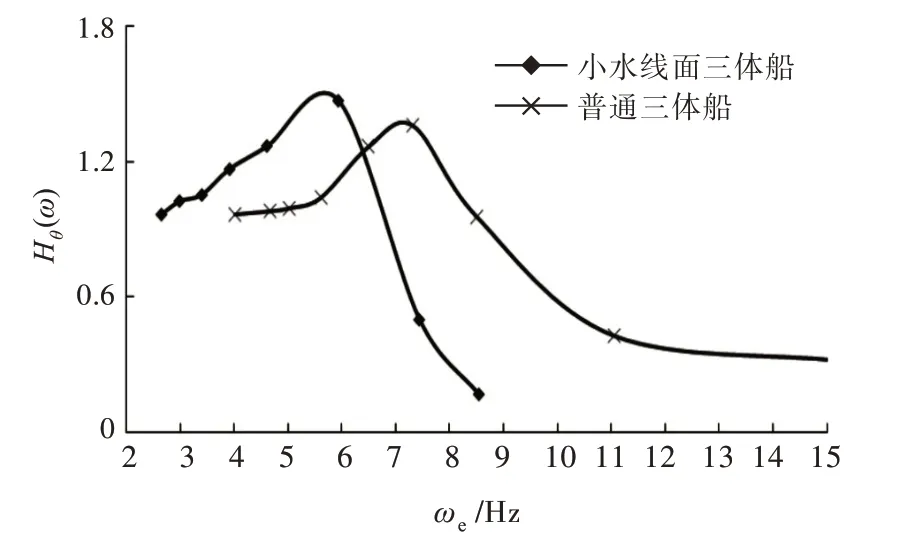
图14 Fr=0.494 时纵摇放大因数对比Fig.14 Comparison of pitch RAO at Fr=0.494

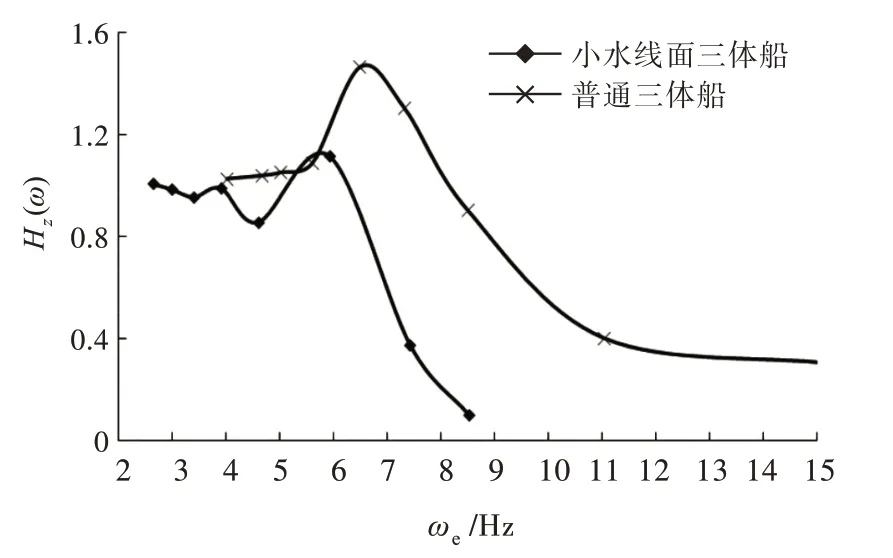
图15 Fr=0.494 时垂荡放大因数对比Fig.15 Comparison of heave RAO at Fr=0.494

由图16 可看出，当遭遇频率ωe＜6 Hz 时，小水线面三体船的纵摇响应幅值大于普通三体船，而当遭遇频率ωe＞6 Hz 时，则小于普通三体船。小水线面三体船纵摇响应幅值的峰值略大于普通三体船，为3.43%。由图17 可看出，小水线面三体船的垂荡响应幅值整体上小于普通三体船，在峰值处比普通三体船小37.54%。结果表明，在高航速下，小水线面三体船的垂荡响应幅值优于普通三体船，纵摇响应幅值无明显优势。

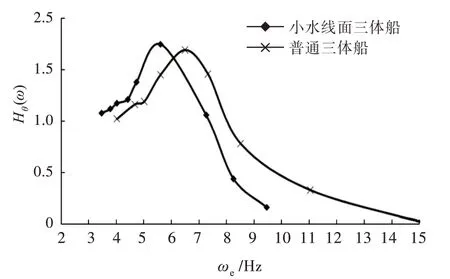
图16 Fr=0.701 时纵摇放大因数对比Fig.16 Comparison of pitch RAO at Fr=0.701

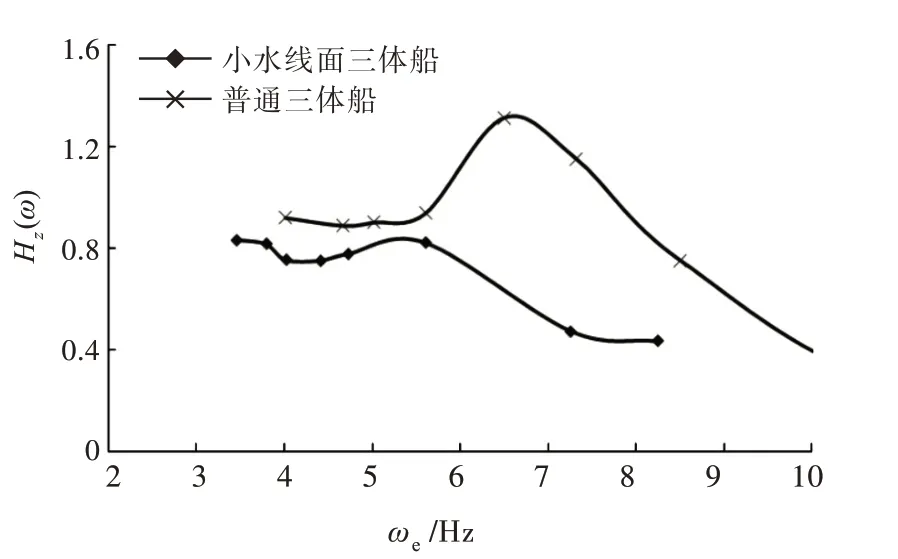
图17 Fr=0.701 时垂荡放大因数对比Fig.17 Comparison of heave RAO at Fr=0.701

3.3 侧体位置对小水线面三体船耐波性的影响

为考虑侧体位置对小水线面三体船耐波性的影响，选取低速到高速（Fr=0.234，0.494，0.701）3 种情况，设置波幅A=20 mm，以RAO 法分析表3中4 种侧体布局方案对小水线面三体船纵摇与垂荡性能的影响，结果如图18～图23 所示。

为便于分析，针对小水线面三体船4 个方案中侧体纵向位置的不同，即b＞0，b=0 和b＜0，分为了3 种类型：后三体（方案1，4，其中方案4 的横向跨距更大）、中三体（方案3）和前三体（方案2）。可得到如下结论：

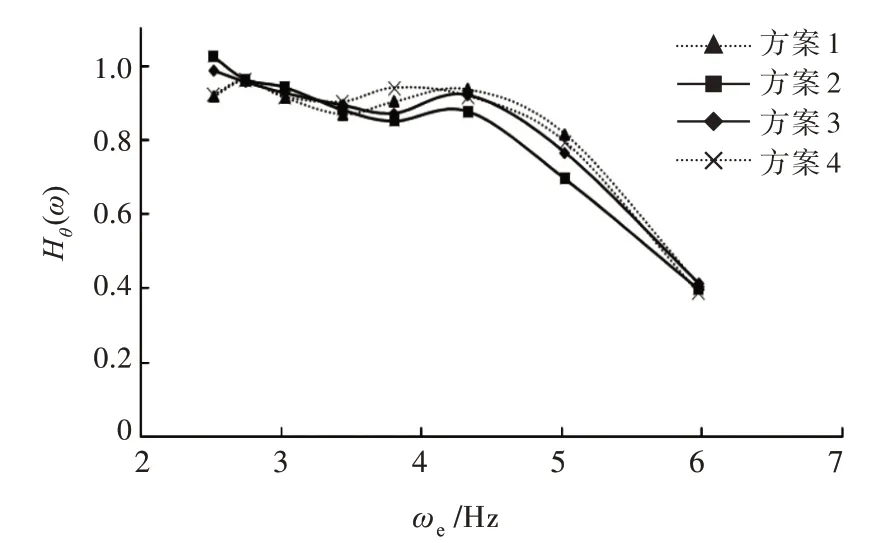
图18 不同方案下纵摇放大因数对比（Fr=0.234）Fig.18 Comparison of pitch RAO at different schemes（Fr=0.234）

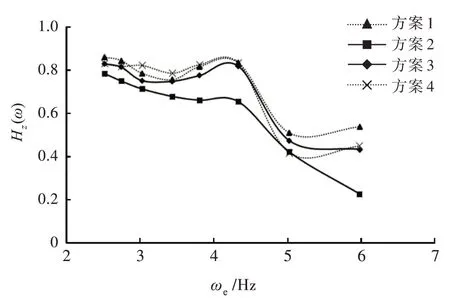
图19 不同方案下垂荡放大因数对比（Fr=0.234）Fig.19 Comparison of heave RAO at different schemes（Fr=0.234）

1）Fr=0.234时，固定侧体横向坐标（a=400 mm），改变侧体纵向位置（方案1，2，3），由图18 可知，当遭遇频率ωe＜3.5 Hz 时，各方案之间纵摇响应幅值的差距不大；当遭遇频率ωe＞3.5 Hz 时，方案2具有较小的纵摇响应幅值，方案1 的纵摇响应幅值最大，其中方案1 比方案2 的纵摇响应幅值峰值大6.73%。由图19 可知，方案2 具有较小的垂荡响应幅值，方案1 的最差，方案1 和方案2 相比垂荡响应幅值峰值约大27.87%。在低航速时，侧体位于舯前整体上耐波性最优，侧体横向位置变化（方案1 与方案4）对耐波性的影响不明显。

2）当Fr=0.494 时，由图20 可知，方案2 纵摇响应幅值整体上优于其他2 种方案，和最差的方案3 相比峰值约小13.11%。由图21 可知，当遭遇频率ωe＜6.5 Hz 时，方案2 的垂荡响应幅值最小，此时方案4 的垂荡响应幅值最大。当遭遇频率ωe＜6.5 Hz 时，方案2 的垂荡响应幅值略大于其他方案。对比侧体不同横向位置，由图20 可知，在遭遇频率ωe=4～6.5 Hz 区间，越靠近主船体纵摇响应幅值越小，当遭遇频率ωe＞7 Hz 时，方案1 与方案4 差别不大；由图21 可知，侧体越靠近主船体，垂荡响应幅值越小。

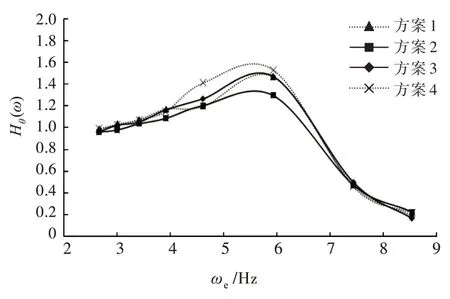
图20 不同方案下纵摇放大因数对比（Fr=0.494）Fig.20 Comparison of pitch RAO at different schemes（Fr=0.494）

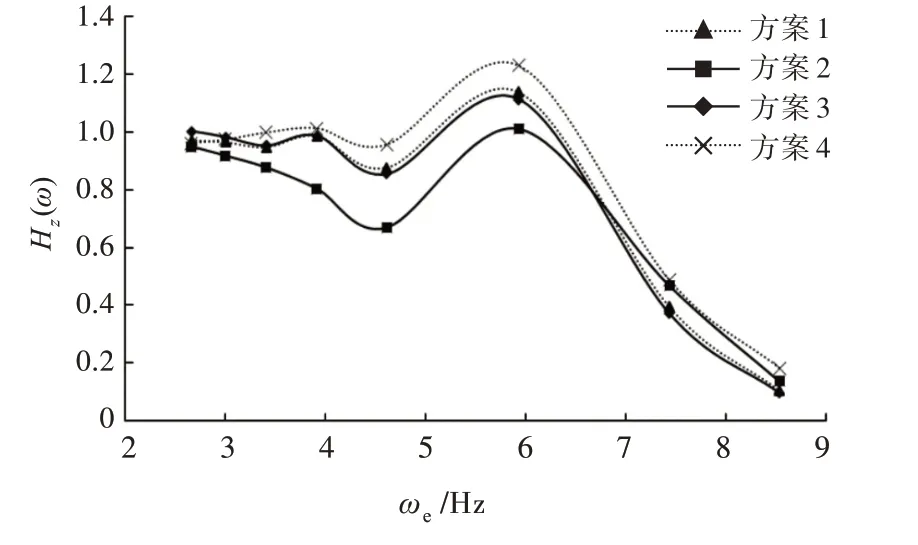
图21 不同方案下垂荡放大因数对比（Fr=0.494）Fig.21 Comparison of heave RAO at different schemes（Fr=0.494）

3）Fr=0.701 时，由图22 可看出，当遭遇频率ωe＜6.5 Hz 时，方案2 的纵摇响应幅值小于其他方案；当遭遇频率ωe＞6.5 Hz 时，方案3 的纵摇响应幅值略小于其他方案。由图23 可以看出，当遭遇频率ωe＜6.9 Hz 时，方案2 的垂荡响应幅值显著小于其他方案，而当遭遇频率ωe＞6.9 Hz 时，各方案之间的差距不明显；整体上，方案2 的纵摇响应幅值峰值和最差的方案1 相比小13.09%。对比侧体不同横向位置（方案1 对比方案4）发现，纵摇响应幅值随着靠近主船体会略微减少，而垂荡响应幅值则几乎相同。

整体上，随着航速的增加，各种侧体布局的小水线面三体船的纵摇与垂荡响应幅值均有所提高，这主要是由于随着航速的增加，波浪对船舶的耐波性影响增大。

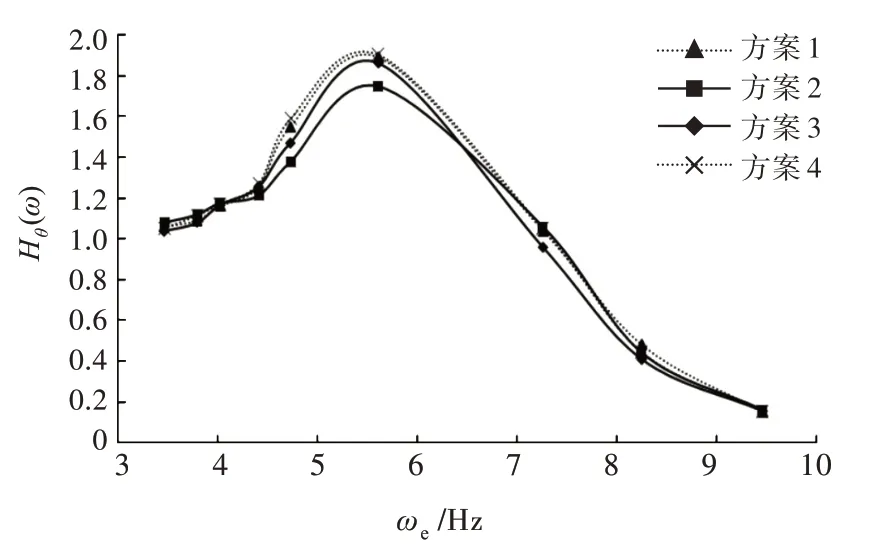
图22 不同方案下纵摇放大因数对比（Fr=0.701）Fig.22 Comparison of pitch RAO at different schemes（Fr=0.701）

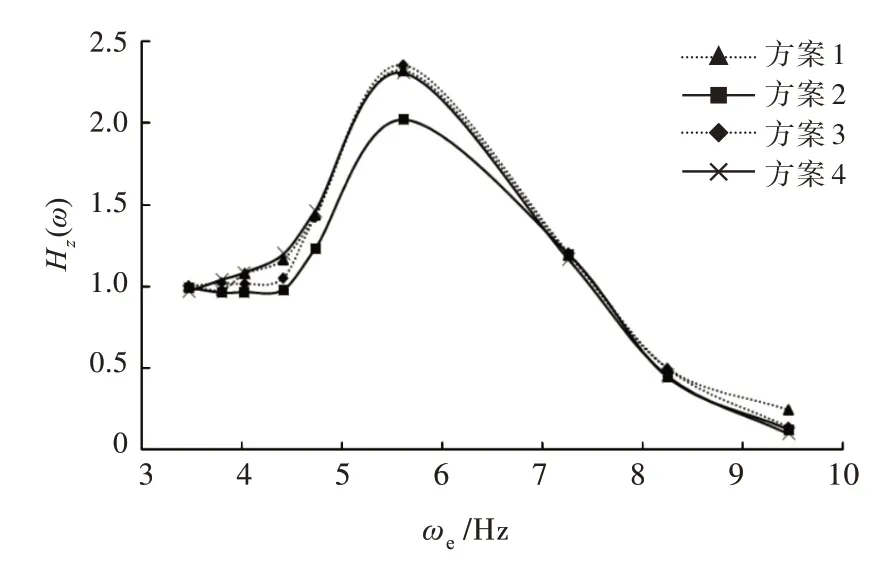
图23 不同方案下垂荡放大因数对比（Fr=0.701）Fig.23 Comparison of heave RAO at different schemes（Fr=0.701）

随着航速的增加，各种侧体布局的小水线面三体船的纵摇与垂荡响应幅值均有所提高，这主要是因为随着航速的增加，波浪对船舶的影响增大。究其原因：前三体在与波浪遭遇时侧体起到了整流的作用，其与主体之间会形成兴波，与主体后部的兴波相连；后三体在遭遇波浪时，侧体与主体会分别产生脱离主体向后传播的兴波和伴随主体向前的兴波，脱离主体的兴波将使侧体产生较大的响应幅值，故后三体的纵摇与垂荡响应幅值大于前三体；随着侧体越来越靠近主船体，侧体受脱离主体方向兴波的影响越来越小，故侧体靠近主体较侧体远离主体的耐波性能好。

4 结 论

本文通过对普通三体船和不同侧体布局下小水线面三体船在规则波中3 种弗劳德数（Fr=0.234，0.494，0.701）情况下的运动响应幅值进行数值模拟，验证了STAR-CCM+平台对三体船耐波性计算的可靠性。结论如下：

1）低航速时，小水线面三体船的垂荡与纵摇响应幅值总体上优于普通三体船；中、高航速时，小水线面三体船的垂荡响应幅值优势较明显，而中速时，小水线面三体船的纵摇响应幅值略高于普通三体船。

2）小水线面三体船的侧体纵向位置对耐波性影响显著，侧体越靠近船艏，垂荡与纵摇性能越好，且响应幅值的优势越明显。侧体横向位置对小水线面三体船耐波性的影响小于纵向位置变化的影响，在高航速时，其规律较复杂，在中、低航速时，后三体船的侧体越靠近主体，运动响应幅值越小。

本文采用黏性流体理论对小水线面三体船迎浪行驶中耐波性能所做的数值模拟分析，可以为该船型的设计提供一定的借鉴。在研究中，针对小水线面三体船和普通三体船的垂荡与纵摇响应幅值的分析模拟试验采用的是一阶规则波，有关不规则波中的耐波性分析将是下一阶段的研究方向。