带扰动混杂多智能体系统领导–跟随一致性
陈世明,王明雨
(华东交通大学电气与自动化工程学院,江西南昌 330013)
1 引言
过去数十年,许多学者对多智能体的协同控制问题进行了研究[1–3].在这些研究中,具有领导者与跟随者的多智能体系统因其简单性与在实际工程问题中的大量应用而得到广泛研究[2–6].滑模控制具有对扰动变化不灵敏及快速响应的特点,因此滑模控制在多智能体协同控制中也得到广泛应用[1,3,6–7].
一致性是多智能体协同控制中的基本问题.在文献[8]中,Vicsek等为了研究具有生物动力学特征的一种粒子系统的运动现象,首次提出离散时间多智能体模型,并研究了该模型的位置一致性.文献[9]受复杂网络中群一致性现象的启发,对具有时延特性的离散时间多智能体群一致性问题做了研究.文献[10]在离散时间多智能体中加入滑模观测器并给出了滑动模态的新的鲁棒稳定性条件,随后提出一种复合控制方法解决了该系统的一致性问题.实际系统中都有一定的条件限制,例如延迟、扰动等,因此关于某些条件限制下的离散时间多智能体的滑模控制许多学者也做了大量的研究[11–14].对于连续时间多智能体,文献[15]提出了两种连续时间多智能体模型的控制协议,对该模型的收敛性做了分析,并将无向图的代数连通度概念推广到有向图中.文献[16–17]通过设计扰动观测器解决了系统中常存在的非匹配扰动的问题,并利用Lyapunov和齐次性定理分析了未受扰动系统的包容控制问题.文献[18]通过使用光滑和非光滑的Lyapunov函数,给出了N–维连续时间非自治系统有限时间稳定的两个充分条件和一个必要条件.文献[19]考虑了在不可靠的信息交换和动态切换拓扑下多智能体系统的一致性问题,提出该系统能够实现一致的充要条件.针对带扰动的连续时间多智能体系统,许多学者使用滑模控制方法也研究了其一致性问题[20–22].
混杂多智能体系统由连续与离散时间智能体组成.文献[23]研究了一阶混杂多智能体系统的一致性问题,分别给出了3种通信状态的混杂多智能体系统模型,随后提出了控制协议和该模型实现一致性的充要条件.文献[24]对混杂切换系统做了研究,提出该系统渐近稳定的充分条件.一般来说,混杂意味着性质或者组成上的异质.因此,文献[25–26]针对异质多智能体系统进行了研究,提出该系统实现一致性的方法.文献[27–28]随后研究了具有固定通信拓扑的异质相依群组系统一致性追踪问题,为了实现一致性,提出了离散更新和连续更新两种方案.上述方法都为混杂多智能体系统实现一致性提供了借鉴.
值得注意的是,在文献[23]中提出了一阶无扰动混杂多智能体系统实现一致性的条件,并使用方程求解的方法研究了该系统的一致性问题.但是目前针对带扰动的混杂多智能体系统的领导–跟随一致性还没有更多的研究,并且滑模控制方法几乎都用于研究异质或者连续/离散时间系统中,很少用于研究混杂多智能体系统.在带有扰动的混杂多智能体系统中,方程求解方法无法解决一致性问题.因此本文采用滑模控制方法研究了带扰动的混杂多智能体系统领导–跟随一致性问题.本文相较于文献[23]有下列3点优势:1)本文研究的混杂多智能体系统中的连续时间智能体是非线性的,更加具有一般性;2)本文研究的混杂多智能体系统存在外界扰动;3)本文采用滑模控制方法提高了混杂多智能体系统对外界扰动的鲁棒性.
2 预备知识
2.1 基本定义
本文中有如下数学定义:N表示正整数集合,R表示实数集合,Rn×m表示n×m维矩阵,定义Im{1,2,···,m}表示连续时间智能体组成的集合,

表示离散时间智能体的集合,In{1,2,···,m,···,n}表示所有的智能体的集合.
2.2 图论
2.3 带扰动混杂多智能体系统
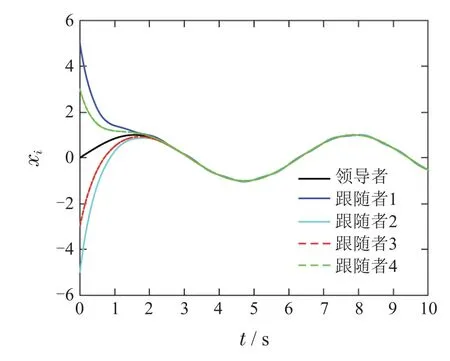
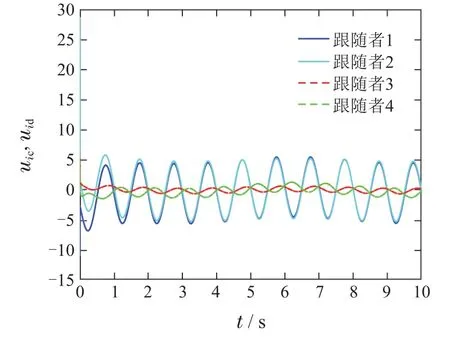
混杂多智能体系统由连续与离散时间智能体组成.领导者动态方程为其中x0(t)是领导者的位置,u0(t)是领导者的输入.跟随者的个数是n,其中连续时间智能体个数是m(m 其中:fi(xi)是光滑的非线性函数;gi∈N;tkkh,k∈N,h代表系统采样周期,htk+1−tk;xi∈R,ui∈R表示智能体的位置与控制输入;di1(t),di2(tk)分别表示某个连续、离散时间智能体的任意动态扰动类型. 定义1在任何初始状态下,带扰动混杂多智能体系统(1)实现领导–跟随一致性满足条件: 假设1对于由混杂多智能体系统(1)构成的有向图G,有向图G中至少存在一个从领导者发出的有向生成树,且领导者的状态信息是已知的时间函数. 带扰动混杂多智能体系统(1)中的跟随者智能体都会受到扰动与其相邻智能体的影响,此时需要设计适当的滑模控制协议实现混杂多智能体系统(1)的领导–跟随一致性.假设混杂多智能体系统中所有的智能体在采样时间更新运动状态与控制输入,并且所有连续时间智能体可以实时观测到自身的运动状态,接下来设计滑模控制协议. 对混杂多智能体系统中连续与离散时间智能体设计滑模控制协议.首先,设计混杂多智能体系统一致性误差协议: 为保证一致性误差协议式(4)–(5)的收敛,带扰动混杂多智能体系统滑模面函数考虑为 其中ci1,ci2为滑模面系数. 混杂多智能体系统中连续时间智能体的滑模面函数采用式(6)时,设计如下滑模控制协议: 其中: ci1是滑模面系数,对于某个连续时间智能体i:是某个连续时间智能体j的输入,在采样时刻ujc(t)ujc(tk),fifi(tk),fjfj(tk),ujd(tk)是某个离散时间智能体j的输入,将在下面给出.x0(t)是领导者的位置,k∈N,且k>D,D|di1|. 定理1对于由混杂多智能体系统(1)构成的有向图G,当式(1)中连续时间智能体的控制协议采用式(8)时,系统(1)中的连续时间智能体可以实现领导–跟随一致性. 证选取Lyapunov函数 对Lyapunov函数求导 根据式(1)可知, 式(11)代入式(10)中: 将控制协议式(8)代入式(13)中: 扰动di1有界,|di1|D,因为k >D,对于此时始终满足 因此,混杂多智能体系统中连续时间智能体的运动状态将会趋近于滑模面si(t)0,一致性轨迹误差式(4)将会沿着滑模面函数收敛到零,混杂多智能体系统中连续时间智能体实现领导–跟随一致性,此时定义1中一致性条件式(3)成立.证毕. 接下来针对混杂多智能体系统中的离散时间智能体设计滑模控制协议.当混杂多智能体系统中离散时间智能体的滑模面函数采用式(7)时,设计如下滑模控制协议: 定理2对于由混杂多智能体系统(1)构成的有向图G,当(1)中离散时间智能体的控制协议采用式(16)时,系统(1)中的离散时间智能体可以实现领导–跟随一致性. 证取Lyapunov函数为V0(tk) 根据Lyapunov稳定性定理,当∆V0(tk)满足 si(tk)0时,离散滑模是存在且可到达的.因此,离散时间智能体滑模控制稳定收敛条件为 由滑模面函数式(7)得si(tk+1)ci2ei(tk+1),将式(5)代入式(7)得 其中 根据式(1)可得 将式(19)代入式(18)中: 将控制协议式(16)代入式(20)中得si(tk+1)si(tk)+h[−εsgn(si(tk))−qsi(tk)],此时 令2 −qh ≫hε,因此 根据定理1与定理2可知,对于任意一个智能体,在某个采样时间tk均满足i ∈In,此时定义1中的一致性条件式(2)成立,混杂多智能体系统(1)满足定义1中的条件式(2)–(3),系统(1)实现了领导–跟随一致性.证毕. 本文在MATLAB平台上对所提出的算法进行仿真实验.考虑1个领导者和4个跟随者组成的混杂多智能体系统,领导者标记为0,跟随者标记为1–4,其中:1–2表示连续时间智能体,3–4表示离散时间智能体.图1表示具有领导者的带扰动混杂多智能体系统的通信拓扑. 图1 带扰动混杂多智能体系统通信拓扑Fig.1 The communication topology of the hybrid multi-agent systems with disturbances 领导者的运动方程:x0(t)sin t,初始位置为x0[0,0]. 跟随者1的滑模面函数取为s1(t)e1(t),跟随者2的滑模面函数取为s2(t)e2(t).跟随者3的滑模面为s3(tk)e3(tk).跟随者4的滑模面为s4(tk)e4(tk).连续时间智能体中扰动为d11,21(t)5 sin(2πt).跟随者1的参数为f1(x1)−bi1(0),k10.跟随者2的参数为f2(x2)−k10.跟随者1–2的初始位置为[−5,0],[5,0].跟随者3–4的参数是ε5,q30,外界扰动d32,42(tk)1.5 sin(2πtk).采样周期h是0.01 s,跟随者3–4的初始位置为[3,0],[−3,0]. 仿真时分别考虑无扰动混杂多智能体系统、带扰动混杂多智能体系统.仿真结果为图2–5所示. 图2 无扰动混杂多智能体系统领导–跟随一致性Fig.2 Leader-follower consensus of the hybrid multi-agent systems without disturbances 图3 无扰动混杂多智能体系统控制输入Fig.3 The control input of the hybrid multi-agent systems without disturbances 图4 带扰动混杂多智能体系统领导–跟随一致性Fig.4 Leader-follower consensus of the hybrid multi-agent systems with disturbances 图5 带扰动混杂多智能体系统控制输入Fig.5 The control input of the hybrid multi-agent systems with disturbances 可以看出上述两种情况下跟随者的运动轨迹与领导者的运动轨迹达成一致,混杂多智能体系统实现了领导–跟随一致性. 本文使用滑模控制方法研究了带扰动混杂多智能体系统的领导–跟随一致性问题.首先,假设了混杂多智能体系统的通信拓扑.其次,设计滑模控制协议实现了混杂多智能体系统的领导–跟随一致性并且验证了混杂多智能体系统在滑模控制下的稳定性.本文设计的滑模控制协议提高了混杂多智能体系统的鲁棒性,将滑模控制运用到混杂多智能体系统中起到了较好的效果.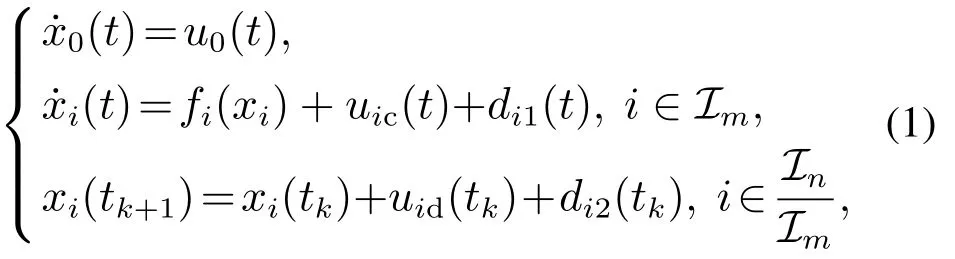

3 混杂多智能体系统滑模控制协议设计






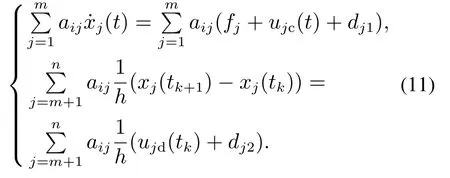
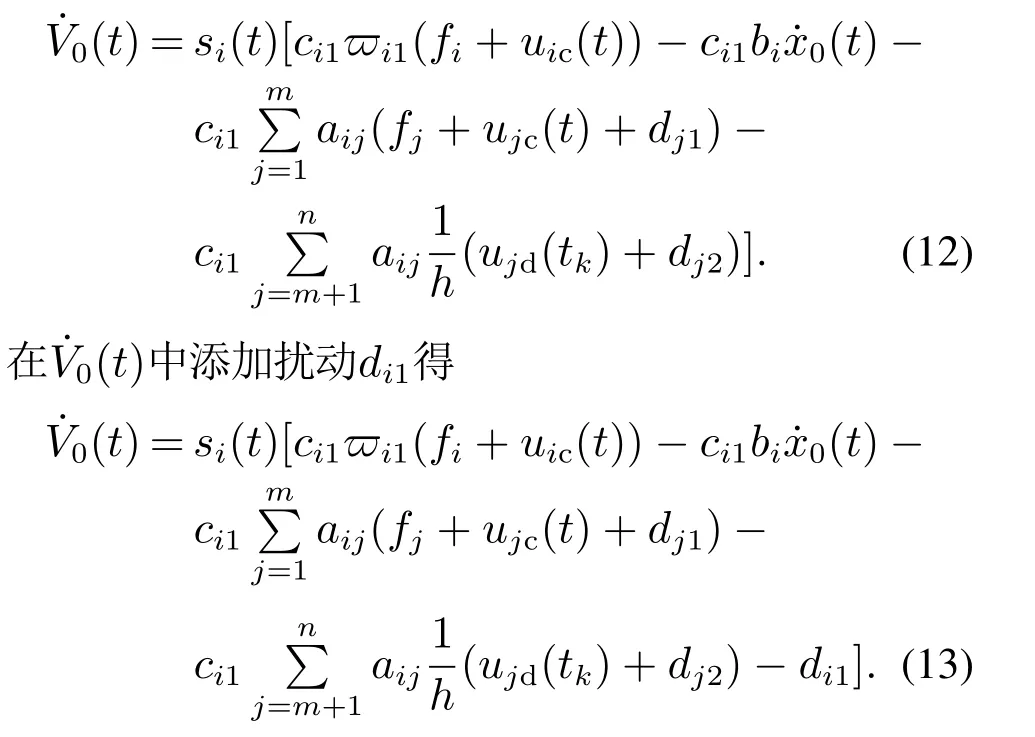

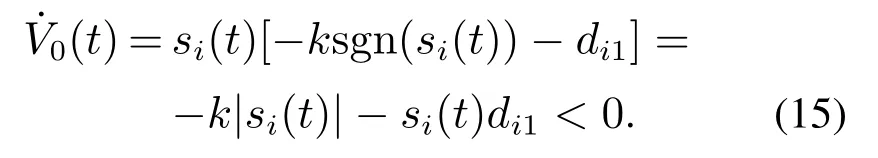
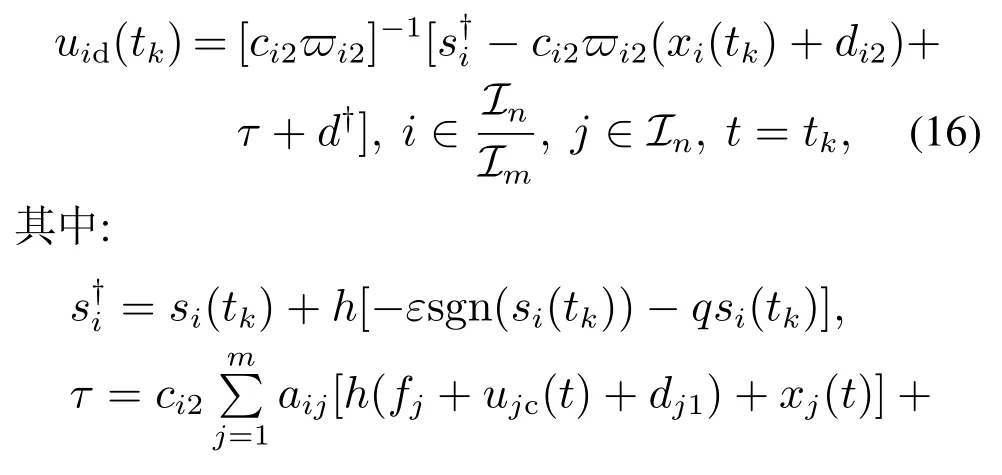

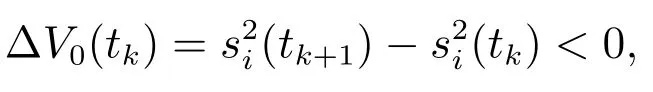

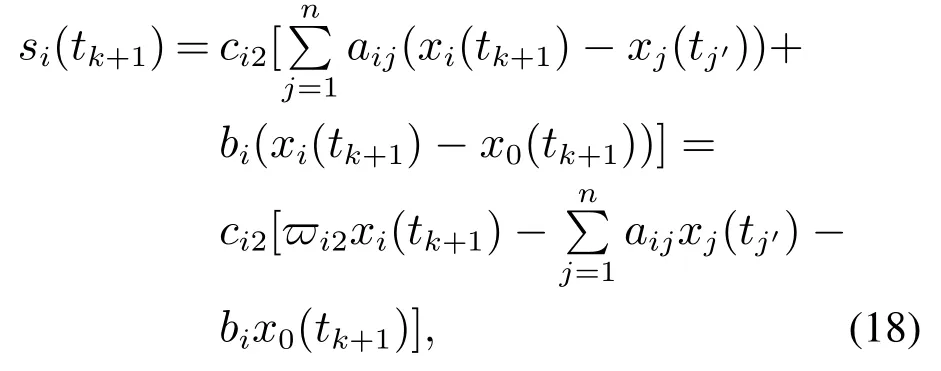






4 仿真分析



5 结论
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

