一种基于时分数据调制的加权分数阶傅里叶变换通信方法

张笑宇， 冯永新

(沈阳理工大学 辽宁省信息网络与信息对抗技术重点实验室， 辽宁 沈阳 110159)

0 引言

加权分数阶傅里叶变换(WFRFT)技术是一种典型的单载波和多载波组合的混合载波调制新技术，作为一种新型的时频分析手段，在通信领域被日渐重视[1-2]。这种新调制技术不仅具备单载波调制的强抗多普勒能力，而且具有多载波调制的强抗多径能力，未来必将成为通信领域的一项重要技术。

由于基于4项WFRFT(4-WFRFT)的周期固定，唯一可变的参数即为旋转因子，单参数下的4-WFRFT很容易被窃听方检测到变换参数和方式，大大降低了4-WFRFT的安全性。文献[3]提出一种基于WFRFT的混合载波与码分多址(CDMA)联合传输方法。通过与CDMA技术相结合，使得信号能量均匀地分布在时频平面上，具有较现有传输方法更优的系统误码性能；文献[4]中提出一种基于并行组合扩频码的基于WFRFT保密通信方法，通过不同的扩频码序列与加权因子复合，动态地利用信息本身进行加密，与传统的直接序列扩频系统相比，可有效提高保密通信系统的安全性能；文献[5]提出一种跳频的改进WFRFT方法，通过子载波跳频的方式打乱离散傅里叶变换(DFT)矩阵的顺序，提高抗截获性；文献[6]提出一种WFRFT与多输入多输出(MIMO)技术相结合的通信方法，采用多层WFRFT调制信号，每层采用不同的调制阶数，可有效抵抗单数扫描。文献[7-15]同样提出了基于WFRFT的改进通信方法。以上基于WFRFT的通信方法均通过与其他技术相结合进一步提升系统的安全性，但可靠性提升程度较小，窃听方仍可有效破译通信信号。

本文在不增加WFRFT变换复杂度的基础上，提出一种时分数据的WFRFT(TM-WFRFT)方法，通过奇偶不同调制的策略减弱信道中噪声对信号的影响，实现基于TM-WFRFT信号的安全通信。

1 4-WFRFT基本原理

通常，4-WFRFT[16]可定义为

s(n)=WFRFT[xi(n),wi(α)]=
w0(α)x0(n)+w1(α)x1(n)+w2(α)x2(n)+
w3(α)x3(n)，

(1)

式中：s(n)为WFRFT后的输出信号，n为数字信号长度；x0(n)为输入信号；xi(n)为x0(n)第i次DFT，i=1，2，3；wi(α)为加权因子，α为旋转因子(或调制阶数)，wi(α)和α满足如下关系：

(2)

k为加权分数阶傅里叶变换的长度。输入信号x0(n)的DFT为

(2)

式中：X0(k)为x0(n)的DFT；N为信号的采样长度。

4-WFRFT可以通过DFT实现，从而降低实现的复杂度[17]，4-WFRFT的实现原理如图1所示。

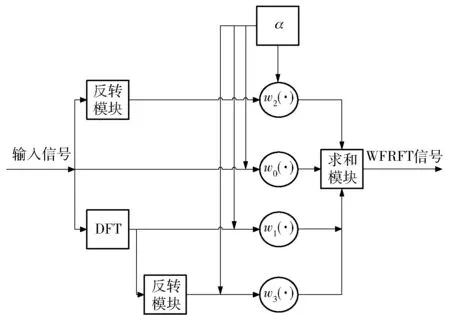
图1 4-WFRFT调制原理图Fig.1 Implementation principle of classic weighted fractional Fourier transform

由于DFT具有周期特性，4-WFRFT具有与DFT相同水平的计算复杂度，4-WFRFT具有可逆性[18]，接收方可以通过-α的WFRFT将信号解调。解调信号可表示为

x0(n)=WFRFT[si(n),wi(-α)]=
w0(-α)s0(n)+w1(-α)s1(n)+
w2(-α)s2(n)+w3(-α)s3(n)，

(4)

式中：s0(n)为解调信号；si(n)为s0(n)第i次的DFT.

4-WFRFT的周期固定，唯一可变的参数即为旋转因子α，在窃听方运算能力足够的条件下，单参数下的4-WFRFT很容易被窃听方检测到变换参数和方式，大大降低了4-WFRFT的安全性。

2 TM-WFRFT基本原理

2.1 实现原理

时分数据调制最典型的应用为时分数据二进制偏移载波调制(TM-BOC)技术[19]，该技术除用方波副载波对扩频序列进行二次调制外，通过时分数据调制技术对信息数据进行处理，采用奇位调制偶位不调制的策略，将奇数位码片与信息数据调制，偶数位码片不调制，利用偶数位无数据分量的优点，采用锁相环进行跟踪处理，从而实现高分辨率的跟踪。TM-BOC信号产生原理如图2所示。

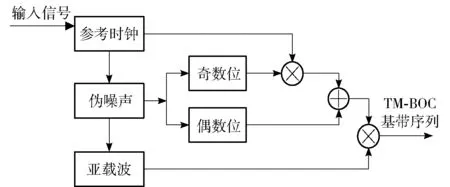
图2 TM-BOC信号产生原理框图Fig.2 Generation principle of TM-BOC signal

传统TM-BOC的时分数据调制模块实现策略为奇位调制、偶位不调制，其分配规则为将奇数位码片与信息数据调制，偶数位码片不调制；而TM-WFRFT的时分数据模块实现策略为奇位和偶位均调制，但调制参数由旋转因子决定，其分配规则为奇数位信息码与旋转因子α调制，偶数位信息码则与旋转因子-α调制。从而可以减弱噪声对信号影响，并利用旋转因子动态加密，提高信号的抗窃听性。TM-WFRFT的实现原理如图3所示。

图3 TM-WFRFT实现原理框图Fig.3 Implementation principle of TM-WFRFT

TM-WFRFT的基本原理如下：采用奇偶不同的调制思想，对旋转因子进行奇偶判定；由于旋转因子为[0,4]区间内的非整数值，奇偶判定的规则设定为获取该旋转因子的小数位数m，将旋转因子乘以10的m次方，再进行整数形式的奇偶判定即可。若判定结果为奇数，则将奇数位信息码进行阶数为α的WFRFT，将偶数位信息码进行阶数为-α的WFRFT；若判定的结果为偶数，则将奇数位信息码进行阶数为-α的WFRFT，将偶数位信息码进行阶数为α的WFRFT. 最后将奇数位的调制结果和偶数位的调制结果相加，即可生成最终的TM-WFRFT信号。

由于只是增加了时分数据调制模块，新调制和传统WFRFT调制均为信息码等长的WFRFT调制和等长的WFRFT解调，具有相同的效率和鲁棒性，对于整个通信过程仍为单参数下的WFRFT. TM-WFRFT的表达式可写为

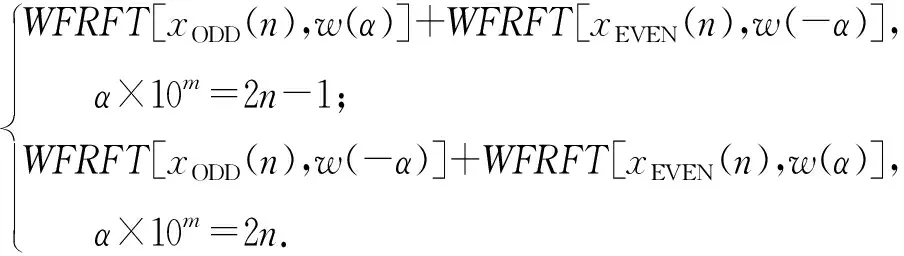
(5)

式中：sTMWFRFT(n)为接收信号；x(n)为发送信息码；xODD(n)为奇数位信息码；xEVEN(n)为偶数位信息码；w′(α)为奇偶判定。

图4 TM-WFRFT与4-WFRFT信号星座图对比Fig.4 Constellation comparison of TM-WFRFT and 4-WFRFT

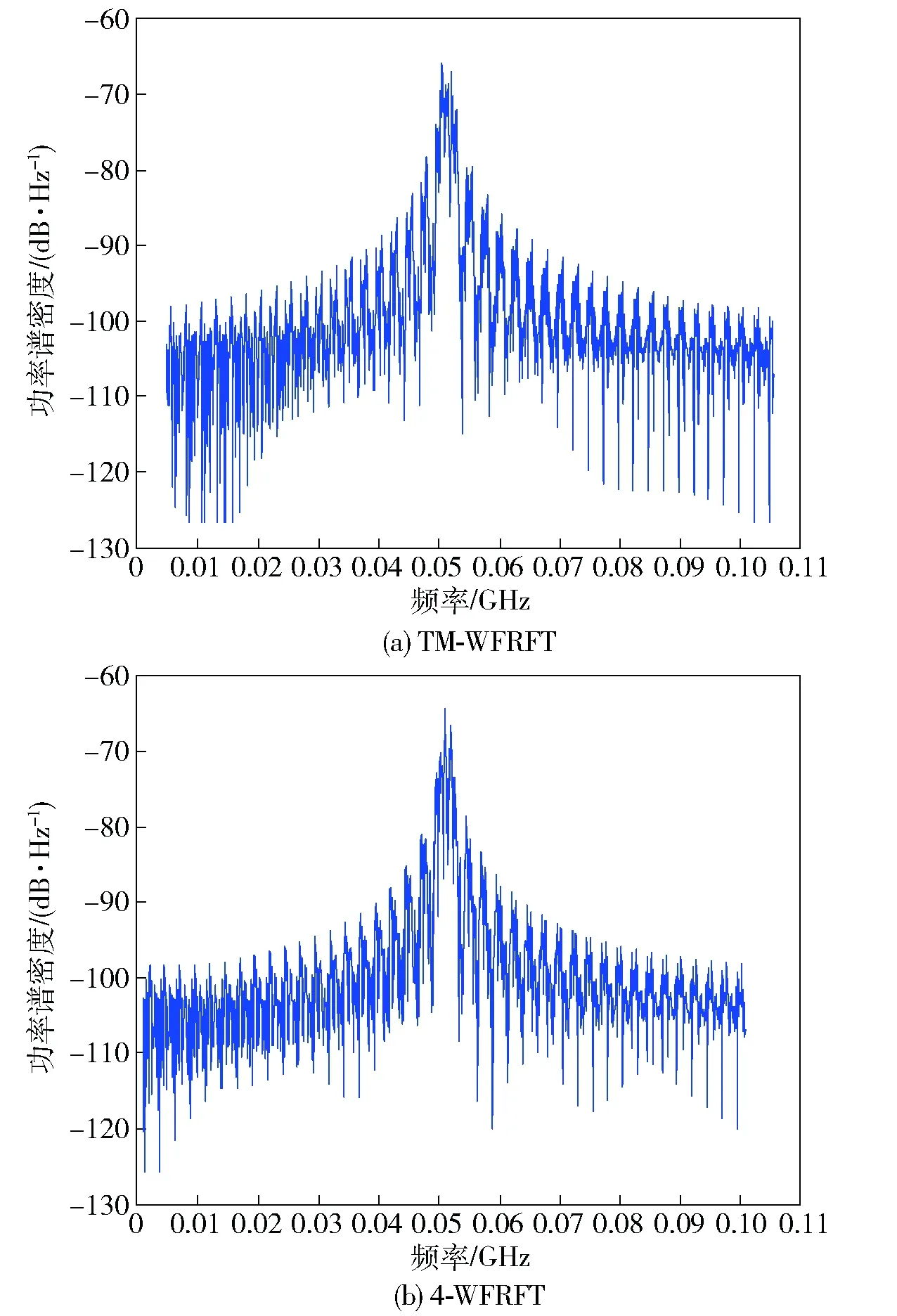
图5 TM-WFRFT和WFRFT信号功率谱对比图Fig.5 Power spectrum densities of TM-WFRFT and WFRFT

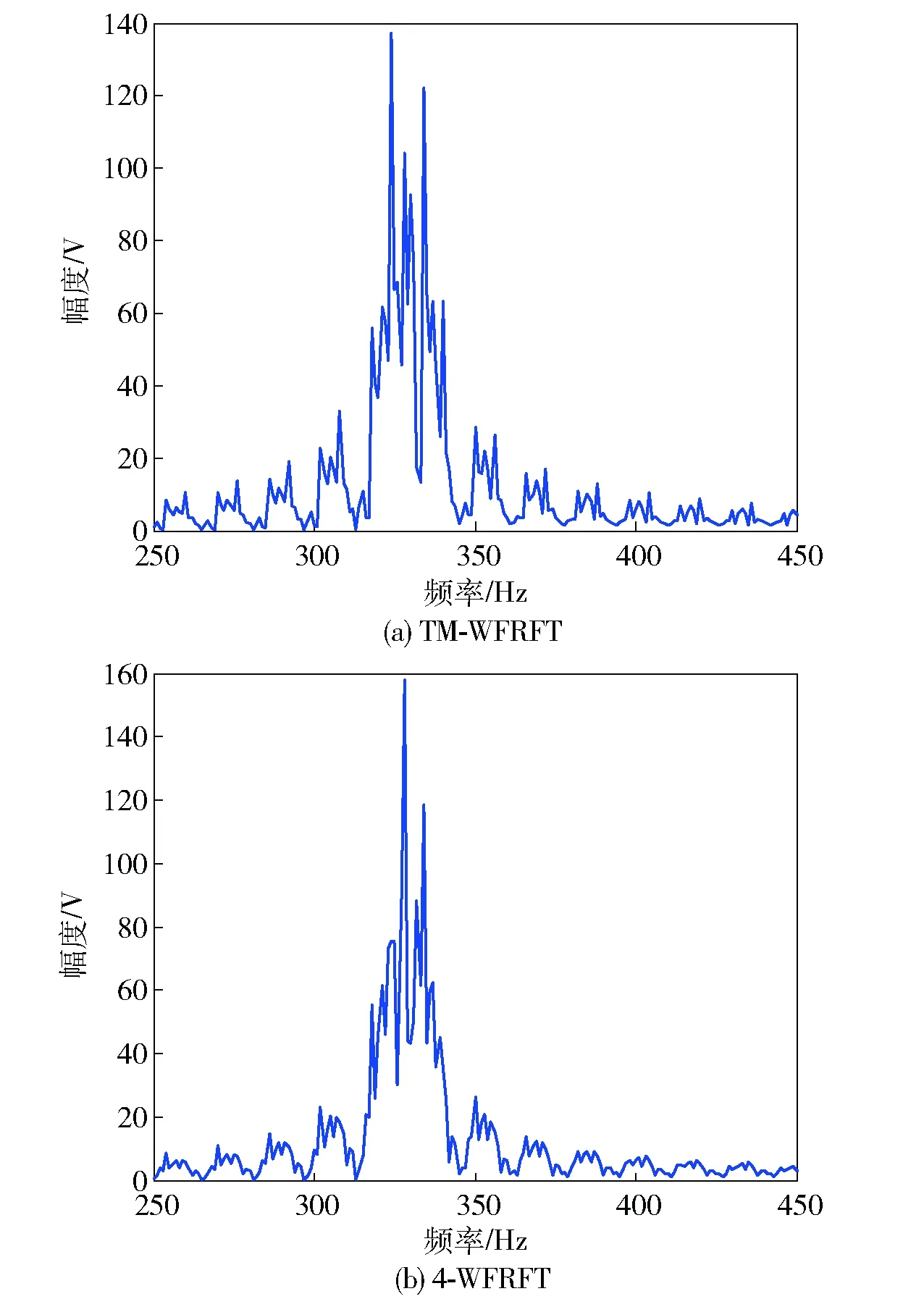
图6 TM-WFRFT与4-WFRFT信号频谱图对比Fig.6 Signal frequency spectra of TM-WFRFT and WFRFT

2.2 调制信号特征

基于正交相移键控(QPSK)调制的TM-WFRFT信号星座图、功率谱及频谱结果如图4～图6所示。与多层WFRFT不同的是，TM-WFRFT并未改变4-WFRFT的星座图混乱程度，仅在信号的频谱幅度上产生了变化。TM-WFRFT虽然采用了奇偶不同的调制策略，并未改变WFRFT信号同相分量和正交分量的关系，因而TM-WFRFT信号和4-WFRFT信号具有相同的星座图。由图5、图6可见：通过产生与4-WFRFT相似的信号形式，使得窃听方仍判定为单参数下的4-WFRFT信号，即使窃听方通过遍历法扫描到正确的旋转因子，也无法正确地解调WFRFT信号，从而提高了通信信号的安全性。

2.3 通信模型

基于上述思想，TM-WFRFT的通信模型如图7所示。在发射机中，将基带信号经过串并转换处理后生成待调制的序列；输入旋转因子进行奇偶规则判定，按照判定结果对生成的待调制序列进行奇偶策略不同的WFRFT调制并添加循环前缀；经过并串转换、D/A转换及上变频，得到TM-WFRFT信号，并通过天线发射。在接收机中，利用天线接收经过信道的TM-WFRFT信号；对接收信号进行下变频、A/D转换、串并转换并移除循环前缀；经过傅里叶变换和频域均衡后，接收机本地同样进行奇偶规则判定，并按照判定结果对信号进行奇偶策略不同的加权分数阶傅里叶逆变换，经过串并转换后解调原始信号。在理想信道条件下，解调的原始信号公式如下：

x′d(n)=TMWFRFT[sTMWFRFT(n),w′(β)]=

WFRFT[sODD(n)+sEVEN(n),w′(β)]=

(6)

式中：sODD(n)为奇位数的接收信号；sEVEN为偶位数的接收信号；β为接收方的旋转因子。由于4-WFRFT具有周期特性，即满足：

WFRFTα{WFRFTβ[x(n)]}=WFRFTα+β[x(n)].

(7)

当β=-α时，接收机最终解调的信号为

(8)

根据一般信道模型，信道噪声模型为高斯白噪声信道和多径瑞利信道，TM-WFRFT是一种兼顾单载波调制和多载波调制的混合载波调制，具有多载波调制的强抗多径能力，同时通过时分数据调制减弱信道中噪声对信号影响，具有更强的抗高斯噪声能力。

2.4 性能分析

对于TM-WFRFT合法通信方，时分调制模块对于整个通信仅增加了时分调制和时分解调，其复杂度远小于传统WFRFT调制中快速傅里叶变换(FFT)模块的复杂度，但时分数据调制中无论旋转因子奇偶性，都等价于对一半信息码进行加密，即在几乎不增加复杂度的基础上加倍提升传统WFRFT调制的可靠性。

图7 TM-WFRFT通信模型Fig.7 Communication model of TM-WFRFT

以旋转因子奇数为例进行分析，旋转因子偶数的原理与此类似，不再赘述。TM-WFRFT合法接收方接收的信号可表示为

y(n)=sTMWFRFT(n)+N(n)=
WFRFT[xODD(n),w(α)]+
WFRFT[xEVEN(n),w(-α)]+N(n),

(9)

式中：N(n)为信道噪声。信道噪声满足(10)式：

NEVEN(n)≈NODD(n)≈N(n)，

(10)

式中：NODD(n)为奇数位的信道噪声；NEVEN(n)为偶数位的信道噪声。

经过信道后，当旋转因子和发射机一致时，TM-WFRFT合法接收机最终解调的信号为

x′TMWFRFT(n)=TMWFRFT[y(n),w′(-α)]=
WFRFT[yODD(n),w(-α)]+
WFRFT[yEVEN(n),w(α)]=
WFRFT[sODD(n)+NODD(n),w(-α)]+
WFRFT[sEVEN(n)+NEVEN(n),w(α)]=
xODD(n)+WFRFT[NODD(n),w(-α)]+
xODD(n)+WFRFT[NEVEN(n),w(α)]=
x(n)+WFRFT[NODD(n),w(-α)]+
WFRFT[NEVEN(n),w(α)]=x(n)+N(n)，

(11)

式中：yODD(n)为接收到的奇数位信息码；yEVEN(n)为接收到的偶数位信息码。

而经过信道后，当旋转因子和发射机一致时，4-WFRFT合法接收机最终解调的信号为

x′WFRFT(n)=WFRFT[y(n),w′(-α)]=
WFRFT[yODD(n),w(-α)]+
WFRFT[yEVEN(n),w(-α)]=
WFRFT[sODD(n)+NODD(n),w(-α)]+
WFRFT[sEVEN(n)+NEVEN(n),w(-α)]=
xODD(n)+WFRFT[NODD(n),w(-α)]+
xEVEN(n)+WFRFT[NEVEN(n),w(-α)]=
x(n)+WFRFT[NODD(n),w(-α)]+
WFRFT[NEVEN(n),w(-α)]=
x(n)+WFRFT[N(n),(-α)].

(12)

由于经过WFRFT会使得幅度值变大，经过WFRFT的噪声幅度值同样被放大。通过对比(11)式和(12)式可知，噪声将会对TM-WFRFT数据信号产生更小的影响，TM-WFRFT具有更低的误码率，通信可靠性更高。

同样，必须对TM-WFRFT窃听方进行误码性能分析，以判断TM-WFRFT的安全性。TM-WFRFT窃听方通过搜索法遍历得到正确的旋转因子后解调的信号为

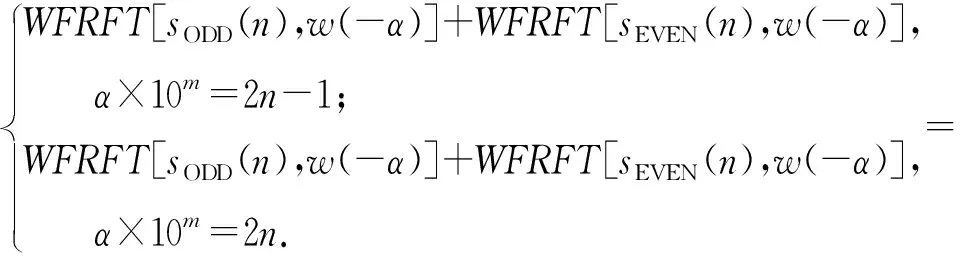
(13)

根据(13)式，在相同接收信噪比条件下，由于经过时分数据调制，奇数位和偶数位采用不同的调制，与4-WFRFT相比，即使通过搜索法遍历得到正确的旋转因子，TM-WFRFT的窃听方只能解调部分传输信息，具有更高的误码率，因此TM-WFRFT所传输信息的安全性更高。

3 仿真与分析

在数值仿真软件MATLAB 7.1环境下，通过分析误比特率，验证TM-WFRFT的性能。定义误比特率为最终解调信息比特在原始信息比特中占有的误差百分比。仿真参数设定为：调制方式QPSK，载波振幅1 V；载波频率51.25 MHz；采样频率1.025 GHz；信息码周期200 ns；32 bit的原始信息码为[0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 0 1 1 0]；旋转因子0.7；信道为多径瑞利信道。

在不同信噪比下，对本文提出方法的可靠性进行仿真验证，TM-WFRFT和4-WFRFT的误比特率对比如图8所示。

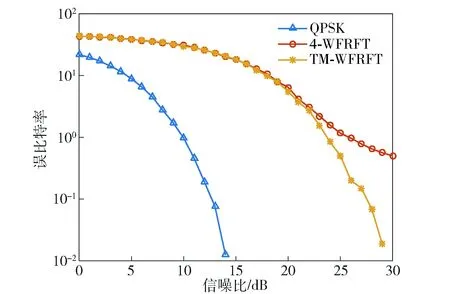
图8 不同信噪比下误比特性能对比Fig.8 BER comparison of TM-WFRFT and 4-WFRFT under different SNRs

由图8中可以看出：在不同信噪比下，TM-WFRFT的误比特率均低于传统的4-WFRFT，特别是在22～30 dB信噪比条件下，TM-WFRFT明显具有更低的误比特率。当满足正常通信的误比特率要求时，TM-WFRFT比4-WFRFT可以提高约3 dB信噪比，这是因为经过时分数据调制，噪声分量对整体信号的影响变小了。故此，与4-WFRFT相比，本文提出的TM-WFRFT方法具有更高的可靠性。

在不同信噪比且窃听方通过搜索正确遍历到旋转因子的条件下，对本文提出方法的安全性进行仿真验证，TM-WFRFT合法接收方和TM-WFRFT窃听方及4-WFRFT合法接收方和4-WFRFT窃听方的误比特率对比如图9所示。

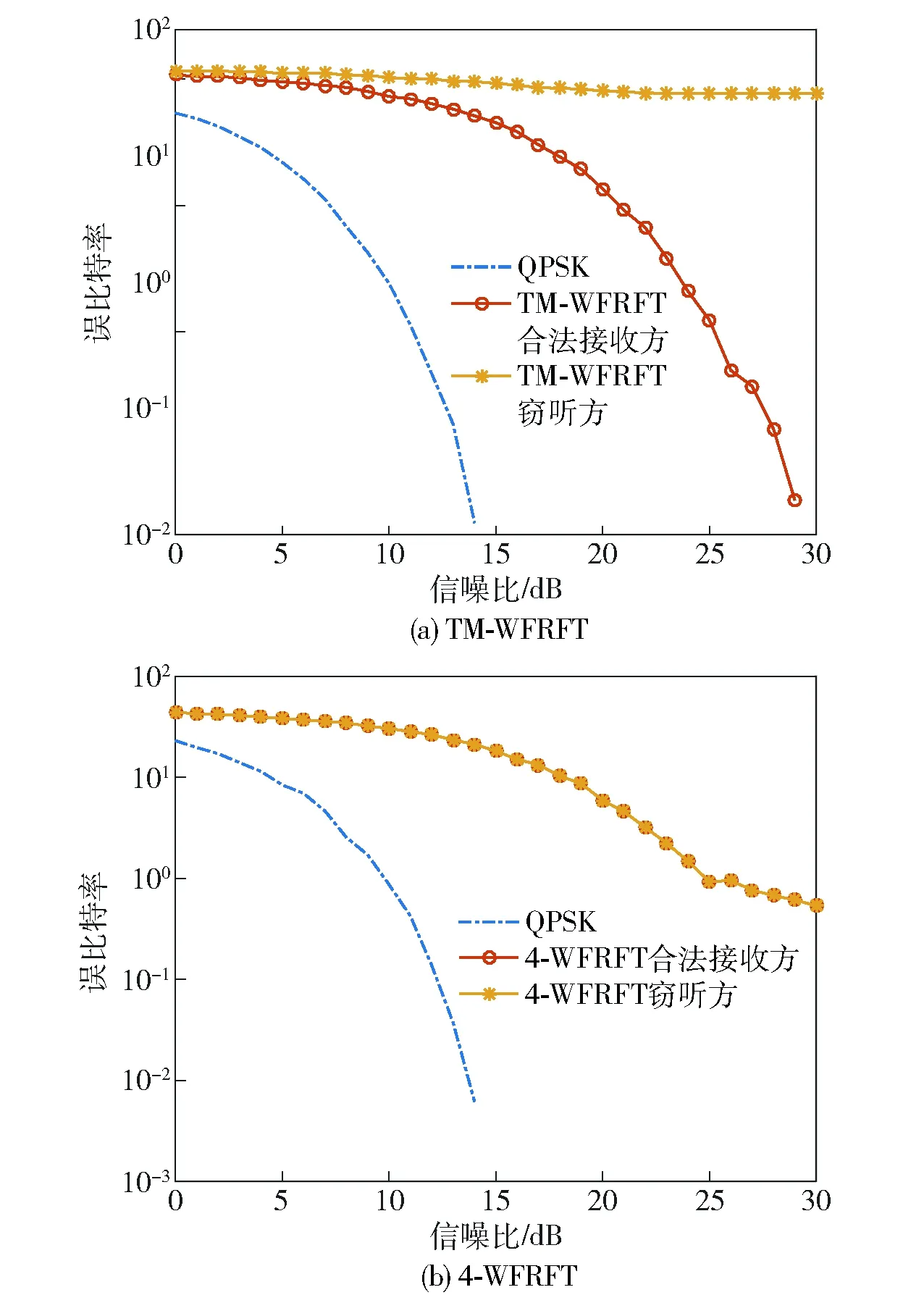
图9 合法接收方和窃听方误比特性能对比Fig.9 BER comparison of legal receiver and eavesdropper

由图9中可以看出：在相同接收信噪比条件下，TM-WFRFT窃听方的误比特率均明显高于TM-WFRFT合法接收方，且窃听方的误比特率基本达到50%，这是因为即使获得了正确的旋转因子，经过时分数据调制，窃听方仍无法准确地解调奇偶不同的调制信号，窃听性能很差；4-WFRFT窃听方的误比特率则与合法接收方基本一致，一旦获得了正确的旋转因子，就可以成功破解获得正确的信息。由此可见，本文提出的TM-WFRFT方法具有更高的安全性。

旋转因子是体现4-WFRFT最重要的因素之一，因此，从旋转因子的对比分析TM-WFRFT比4-WFRFT上具有更好的接收性能。信噪比均为5 dB条件下，TM-WFRFT和4-WFRFT的误比特率如图10所示。

图10 不同旋转因子下误比特性能对比Fig.10 BER comparison of TM-WFRFT and 4-WFRFT under different rotation factors

由图10中可以看出：在一个周期旋转因子内，TM-WFRFT的误比特率和4-WFRFT具有相同的变化规律，当旋转因子取值范围为[0,1]和[2,3]时，误比特率均呈现上升趋势；当旋转因子取值范围为[1,2]和[3,4]时，误比特率均表现下降趋势。但在整个周期内，TM-WFRFT的误比特率随着旋转因子变化较为平滑，受旋转因子的变化影响较小，而4-WFRFT则变化较为波动，受旋转因子影响较大。因此TM-WFRFT比4-WFRFT具有更好的接收性能。

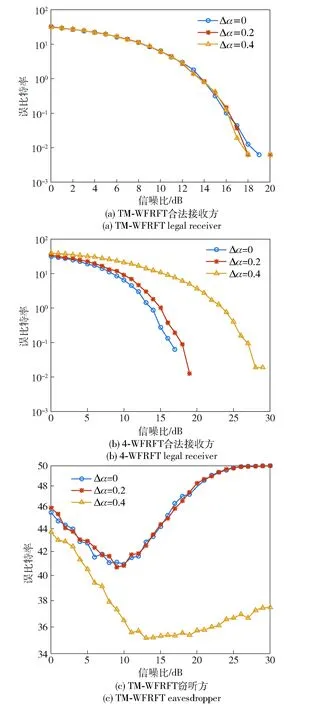
图11 旋转因子偏差下误比特性能对比Fig.11 BER comparison under different rotation factor deviations

进一步，在不同信噪比下，当接收方旋转因子出现偏差时，对接收性能进行验证。旋转因子偏差Δα分别为0.2和0.4，TM-WFRFT合法接收方、4-WFRFT合法接收方及TM-WFRFT窃听方的误比特率对比如图11所示。从图11中可以看出：当接收方旋转因子出现偏差时，TM-WFRFT合法接收方和4-WFRFT合法接收方的接收性能衰减均特别严重，且4-WFRFT的衰减程度更高，对旋转因子的敏感度比TM-WFRFT更高，即对4-WFRFT的合法接收方具有更高要求。对于TM-WFRFT窃听方，其接收性能不随旋转因子偏差的变化而变化，即无论出现怎样的旋转因子偏差，其误比特率均很高，均无法解调有用的信息。因此，TM-WFRFT可有效提升4-WFRFT的安全性。

4 结论

1)在分析4-WFRFT机理的基础上，本文针对单参数WFRFT易被破解的不足，提出了一种基于TM-WFRFT通信方法，该方法充分利用旋转因子动态加密，进行TM-WFRFT调制，提高了4-WFRFT信号的可靠性和安全性。

2)仿真结果表明，TM-WFRFT能够在提高4-WFRFT可靠性的同时显著降低窃听方的破译能力，进一步增强信息传输的安全性。