爆炸型烟幕弹遮蔽效能仿真研究
徐路程, 郝雪颖, 肖凯涛, 宋伟伟, 陈春生
(1.军事科学院 防化研究院, 北京 102205; 2.国民核生化灾害防护国家重点实验室, 北京 102205)
0 引言
烟幕是应用最广泛的一种无源干扰方式,它通过在空中施放大量的气溶胶微粒来改变光辐射的大气传播特性,从而掩盖要保护的目标[1]。烟幕因较高的效费比以及在对抗光电制导武器方面具有显著成效,受到各国军队的普遍重视[2]。按照成烟方式分类,发烟器材可以分为爆炸分散型、燃烧反应型和机械喷射型,其中爆炸分散型采用爆炸方式成烟。初始云团是指发烟剂在爆炸动能的作用下迅速膨胀,当在空气阻力作用下达至平衡时形成的一个球冠状或球形烟团,此后烟团在风、湍流及温差作用下在大气中传播与扩散[3]。关于初始云团的形成过程,学者们已经开展了很多研究工作[4-7]。烟幕仿真对于烟幕战术使用有较强的参考价值,张楠等[8]结合无风条件的高斯模型和红外烟幕消光模型建立了红外烟幕三维空间的透过率模型;花超等[9]、邱继进等[10]运用拉赫特曼扩散理论模拟瞬时体源的扩散过程,分别对烟幕干扰红外导引头和红外制导反舰导弹的效果进行了量化研究。相比于假定风场均匀稳定的高斯模型和拉赫特曼扩散理论,基于计算流体力学(CFD)方法能够得到关注区域中风场的更多结构特征[11],从而提高烟幕扩散和消光模拟的可信度。此外,拉赫特曼扩散理论中只考虑了风场的扩散作用,忽略了源的热效应如烟剂燃烧放热的影响。徐路程等[12]采用CFD方法和离散相模型对连续点源烟幕进行了数值模拟。
为了模拟爆炸型烟幕弹扩散过程中的风场特征和热力效应,本文根据试验数据建立爆炸型烟幕弹初始云团的数学模型,分析烟剂燃烧放热对初始云团的热力效应;运用CFD方法求解模拟区域风场,并运用离散相模型进行扩散模拟;通过计算面密度对烟幕的有效遮蔽区域进行模拟;将模型计算结果与试验数据进行对比,以检验模型的有效性。
1 材料、现场布置及试验
试验中使用爆炸型烟幕弹为圆柱型装药,装药结构如图1所示,中心扩爆药柱为6.3 g钝化黑索今(RDX)炸药,周围发烟剂的主要成分为红磷、氧化剂、钝化包覆剂、黏合剂,质量104 g,其中红磷84 g. 挂弹高度为1.5 m. 试验时大气稳定度为中性层结,气温10 ℃,相对湿度40%,平均风速为2 m/s. 场地下垫面为平坦的裸露地面,布设如图2所示,在挂弹点上风向和下风向分别竖立标杆,摄像方向与风向垂直,高速摄影采用美国DEL Imaging Systems公司生产的MotionXtra HG-LE高速摄像机,拍摄参数为分辨率1 128×752,帧速率1 000帧/s. 通过摄录像及图像分析法[3]对烟幕的长度和高度进行计算。图3所示为试验中爆炸生成的初始云团,经测量,烟幕有效长度为4.91 m,高度为1.21 m.

图1 装药结构图Fig.1 Diagram of charge structure

图2 试验场地布设示意图Fig.2 Schematic diagram of test site layout

图3 试验中初始云团Fig.3 Initial smoke cloud in the test
2 数值模拟
为便于后续风场和扩散的建模和计算,建立坐标系如图4所示:x轴正方向指向下风方向,y轴正方向与摄像方向一致,坐标系为笛卡尔坐标系,z轴正方向按照右手定则竖直向上,爆心在坐标系中的坐标为(100 m,100 m,1.5 m),逆推可得坐标原点的位置。

图4 几何模型及边界条件示意图Fig.4 Schematic diagram of geometric model and boundary condition
2.1 初始云团数学模型
当初始烟幕的体积相对于烟幕的扩散体积不可忽略时[3],应该使用体源模拟发烟源。本文研究的爆炸型烟幕弹符合这种特征。在初始云团的相关理论研究中[4,13],一般假设初始云团内部浓度均匀分布。扩爆后形成的初始云团近似为椭球状,并且一般采用起始半径和高度两个参数来表示尺寸[3,14-15]。初始云团的数学模型假设如下:
1)初始云团使用拉格朗日方法进行描述,即用粒子分布代表初始云团中的浓度分布;
2)初始云团为椭球体;
3)初始云团内浓度均匀分布,即粒子在椭球体内均匀分布。
令初始云团横向半径为r、高度为2h,爆心位置为(xc,yc,zc),则构成初始云团的所有粒子坐标(x,y,z)满足如下椭球方程:
(1)
可以运用MATLAB软件实现上述构造初始云团的方法。具体算法如下:
1)通过MATLAB软件随机生成分别在[xc-r,xc+r]、[yc-r,yc+r]、[zc-h,zc+h]上满足均匀分布的随机数a、b、c;
2)如果(a,b,c)满足上述椭球方程,则表明(a,b,c)是一个随机生成的、椭球面以内的点,否则重新生成;
3)将(a,b,c)加入点序列(xi,yi,zi);
4)重复上述步骤,直至点序列长度达到需要的总生成点数N.
取爆心坐标(xc,yc,zc)为(100 m,100 m,1.5 m),r=2.455 m,h=0.605 m,运用以上方法生成N=10 000的初始云团示意图如图5所示。需要说明的是,在后续扩散模拟时,为匹配高分辨率的网格、保证浓度统计的精度,经无关性检验,实际仿真中使用的粒子数为N=400 000.
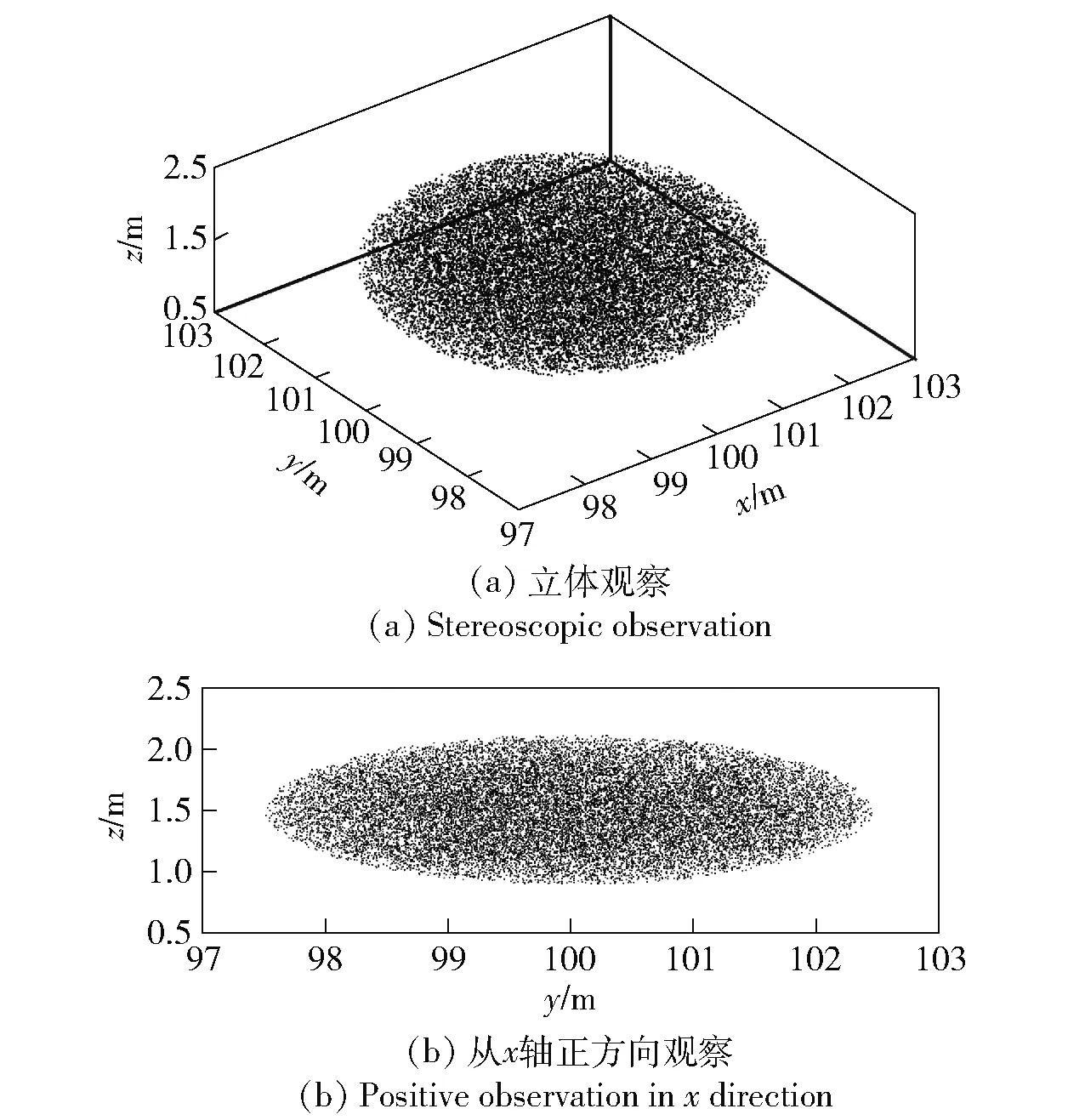
图5 根据试验数据生成的初始云团示意图Fig.5 Sketch map of initial smoke cloud generated from test data
2.2 风场模拟
准确的风场模拟是气溶胶扩散模拟的先决条件,本文采用CFD方法对风场进行数值模拟。气溶胶在空间中扩散是一个三维过程,并且扩散过程一般都发生在大气边界层以内。因此本文中考虑垂直方向的计算高度为50 m,三维的计算区域为400 m(x轴方向)×200 m(y轴方向)×50 m(z轴方向)。
由于大气边界层中流速远小于声速,且初始云团形成后爆炸冲击波对扩散区域的影响基本消失,可以假定大气为不可压缩理想气体。描述不可压缩黏性流体的控制方程采用Navier-Stokes(N-S)方程和能量守恒方程,湍流模型采用雷诺平均(RANS)方法中的标准k-ε模型(k为湍流脉动动能,ε为湍流耗散率)[16]。其中:
1)连续性方程
(2)

2)动量方程
(3)

3)能量方程
(4)

4)湍流脉动动能方程
(5)
式中:μt为湍流黏性系数;σk为湍流脉动动能的普朗特数。
5)湍流耗散率方程
(6)
式中:σε为湍动能耗散率的普朗特数;c1、c2为经验常数。
以上方程组为非线性方程组,需要通过数值方法进行求解。空间上,对计算区域进行网格划分,在爆心附近和地面附近等物理量梯度较大区域,局部进行网格加密。方程的求解使用Ansys Fluent软件完成,动量、能量、湍动能和湍动能耗散率方程使用精度较高的2阶迎风格式进行离散,压力速度耦合采用稳定性高的压力耦合方程的半隐式(SIMPLE)方法。
对于入口边界条件,Richards等[17]建议速度、湍动能、湍动能耗散率使用如下函数廓线表示:
(7)
(8)
(9)
式中:u*为摩擦速度;κ=0.42为卡门常数;zc=0.01 m为地面粗糙长度;cμ为经验常数。对于下边界,采用无滑移壁面边界条件,需要特别注意的是,Ansys Fluent软件中粗糙度用等效砂粒粗糙高度表示,它与上述空气动力学地面粗糙长度之间的关系[17]为
(10)
式中:CS为经验常数。
对于上、侧边界条件,Blocken等[18]建议采用与入口边界保持一致的廓线,从而能够最小地引入流向上梯度,保证流向上的均匀性。出口边界采用自由流边界。对于能量方程,除出口边界以外,各边界温度均为283.15 K.
理论上,更密集的网格能够得到分辨率更高的计算结果,本文采用3种网格划分方式,分别将三维计算域划分为10万、15万和20万网格,并对风场进行稳态计算。如图6所示,不同网格数量情况下,在爆心位置处垂线的风场分布随着网格加密,可以认为计算已经收敛,表明20万网格已经能够合理模拟风场特征,以下扩散模拟在此网格的风场中完成。

图6 网格无关性检验Fig.6 Grid independence test
2.3 初始云团的热力效应
爆炸燃烧成烟的烟幕云团因为燃烧释放的热量作用而温度较高。因此当烟幕云团与周围空气达到压力平衡时,烟幕云团的密度与周围空气相比较小,烟幕云团受浮力作用表现出上升运动[13]。此外,热力作用还会增大湍流强度,使扩散更加强烈。
红磷在空气中与氧气充分燃烧后生成十氧化四磷(P4O10),与空气中的水分相遇后生成具有不同结晶水的正磷酸。由于初始云团的形成过程时间较短,假定此过程中的放热完全由红磷与氧气完全反应提供,此过程的反应热可通过计算P4O10和红磷的标准生成焓差值[19]计算得到,经计算为735.35 kJ/mol. 朱晨光[13]通过试验发现,红磷发烟剂燃烧产物分为两个部分,一部分变成烟幕微粒,形成烟幕云团,另一部分燃烧产物结块落在地面,落在地面的燃烧产物质量占50%. 根据第1节中发烟弹的成分组成,可以计算得到实际形成云团的红磷燃烧放出的全部热量为996.28 kJ,释放出的热量用于加热初始云团。而发烟弹完成近场抛撒后一般在1~3 s内烟团温度与大气温度逐渐达到一致[15]。于是,可以估算初始云团的平均温度为297.45 K.
2.4 扩散模拟
为与拉格朗日方法描述的初始云团相匹配,烟幕扩散采用属于拉格朗日方法的离散相模型[20]进行模拟。
根据牛顿第二定律,拉格朗日坐标下颗粒的动力学方程(以x轴方向为例说明)为
(11)

(12)
(13)

除以上力的作用外,颗粒还受到湍流扩散作用的影响,本文采用随机游走(DRW)模型确定粒子的瞬时速度:

(14)

经烟箱中使用激光粒度仪测量,烟幕的平均粒径dav=1.6 μm. 磷酸的密度取ρ=1 334 kg/m3[21].
2.5 面密度计算
对于网格统计得到的浓度的离散分布,面密度的计算可采用数值积分的方法实现(从y轴负方向进行观察),表示为
(15)
式中:Mik表示面密度矩阵M的分量;cijk表示烟幕浓度;Δy表示浓度cijk对应的光程。
需要说明的是,在计算风场时使用的网格尺度为米量级。从网格无关性检验结果来看,这个量级能够满足描述风场的需要。但在浓度统计及面密度计算时,因为源及扩散尺度都在1~10 m的量级,所以需要分辨率更高的网格来进行描述。本文中采用0.1 m的立方体网格进行浓度统计和面密度的计算。
对于一般的情况,网格3个方向的边长分别为Δx、Δy、Δz,则网格浓度可表示为网格内粒子代表的质量和与网格体积之比为
(16)

对于红磷烟幕,其遮蔽质量与空气的相对湿度密切相关。根据文献[21],在相对湿度为40%时,红磷烟幕的遮蔽质量为Mb=0.36 g/m2. 于是在求得面密度矩阵M的基础上,通过计算面密度等值线,并且绘制遮蔽质量对应等值线以内的范围,即可得到烟幕的有效遮蔽区域。
3 结果分析
下面运用第2节方法,对试验中弹爆后10 s内的烟幕效能进行仿真计算。
通过大量的人眼和心理测试统计可知,只有当透过率小于1.25%时,目标才会被遮蔽,这个透过率与上述遮蔽质量是对应的[1,22]。因此,可以将计算得到的有效遮蔽区域与试验中的烟幕遮蔽区域进行对比验证。第1节试验中烟幕对可见光有效遮蔽区域边界的判读参照文献[3,23]中的方法:将某一时刻烟幕图像与烟幕完全消散后的背景图像对齐,并借助图像分析软件及鼠标以肉眼判读来判读烟幕图像的遮蔽边界,进而确定烟幕有效遮蔽区域的形状、有效烟幕长度和高度。
与风场计算类似,理论上,更多的粒子数会提高计算精度,但同时也会带来更大的计算量。分别采用N为100 000、200 000、400 000共3种粒子数进行仿真计算,烟幕的长度和高度的计算结果分别如图7所示。由图7可见,随着粒子数增长,各时刻的计算结果均已收敛。因此,选用N=400 000的计算结果进行后续的结果分析。

图7 不同粒子数的计算结果Fig.7 Calculated results using different particle numbers
2 s、5 s、10 s 3个时刻试验图像和模拟图像对比如图8所示,在试验图像中用红色实线对烟幕遮蔽边界进行了标识,对应的模拟图像为同一时刻计算得到的有效遮蔽区域。不同时刻有效烟幕长度和高度模拟数据和试验数据的对比如图9所示。

图8 不同时刻的试验图像与模拟图像对比图Fig.8 Comparison between test images and simulated images at different time

图9 模拟数据与试验数据对比Fig.9 Comparison between simulated data and test data
由图8、图9可见,模型能够较好地反映烟幕形状及长度、高度的变化规律。爆炸型烟幕弹在弹爆后由于受到自身的热力作用,垂直方向抬升、扩散明显;当抬升到一定高度后,由于能量散失,温度下降,抬升作用减弱。同时,随着离地高度的增加,风速明显增加,动力效应作用凸显,横向扩散更加明显。相比于拉赫特曼模式,本文模型的计算结果与试验结果更为接近,表明本文模型能够较好地模拟爆炸型烟幕弹前期扩散阶段的作用效能。但随着时间的增加,两种模型的计算结果与试验结果的相对误差均逐渐增大,原因可能在于风向的波动没有在定常模型中合理地反映出来[14],也有文献[24]指出即使根据多次示踪试验数据,同一地点同一类型天气给出的扩散参数,其大小可相差多倍,其不确定度是非常显著的,这个问题有待后续研究逐步完善。
4 结论
本文建立了一个爆炸型烟幕弹遮蔽效能仿真模型。运用拉格朗日方法,通过在椭球体内均匀生成随机粒子的方法构建初始云团,通过分析初始云团的热力效应结合计算流体力学方法和离散相模型,对粒子的扩散进行模拟。最后通过浓度统计和计算面密度得到了烟幕对可见光的有效遮蔽区域。与试验结果和拉赫特曼模式结果对比,证明了本文所提模型的有效性,表明该模型能够在爆炸型烟幕弹的前期扩散阶段较好地反映烟幕形状及长度、高度的变化规律,能够为爆炸型烟幕弹的效能评估提供有效技术手段,为复杂环境下的战术使用提供参考。

