基于动态扭矩测试的综合传动系统主轴低周疲劳寿命预测与验证

王成， 毛飞鸿， 侯威， 张金乐， 邹天刚

(中国北方车辆研究所 车辆传动重点实验室， 北京 100072)

0 引言

传动轴是履带车辆综合传动系统传递动力和运动的关键零件，其使用性能对整个传动系统的功能实现和可靠性都起着至关重要的作用。综合传动系统的传动轴类型多种多样，其中，传动主轴承担直驶时变速机构的动力输出、转向时的汇流功率、中心转向时制动扭矩、制动过程液力减速器的减速扭矩和换挡过程的冲击扭矩等，承载工况恶劣复杂，服役过程中疲劳是其主要失效形式。主轴的疲劳失效导致整个传动系统瘫痪，使整车丧失直驶、转向、制动等功能，车辆将因此失去机动能力。

目前，针对车辆传动系统轴类零件的疲劳问题开展了大量的研究。例如，文献[1-4]针对履带车辆传动系统输出轴，开展了实车扭矩测试，采用雨流计数法对实车数据进行统计研究，获得了传动轴载荷统计规律，结合疲劳线性累计法则对传动轴的疲劳寿命和疲劳损伤进行预测。文献[5-6]建立了履带车辆行驶仿真平台，通过虚拟试验获得了侧减速器传动轴在各种不同工况条件下的动态载荷，计算了传动轴的疲劳寿命，进而仿真分析不同结构对传动轴疲劳寿命的影响规律，并对传动轴的结构进行改进。文献[7-9]针对汽车传动系统的轴类零件，实车测试了不同工况下的动态扭矩，获得了传动轴的疲劳损伤和疲劳寿命。文献[10]针对综合传动系统主轴疲劳样件开展宏微观形貌材料的化学成分、金相分析和力学分析，并建立了传动主轴的有限元模型，研究了传动主轴高周疲劳失效的原因。

本文针对履带车辆综合传动系统主轴低周疲劳失效的问题，实车测试履带车辆在铺面路循环工况下传动系统主轴的动态扭矩，确定导致主轴发生低周疲劳失效的行驶工况和载荷条件，并建立主轴的弹塑性有限元模型，开展主轴弹塑性有限元分析和低周疲劳寿命预测。搭建模拟车辆起步阶段的综合传动系统试验台，开展主轴低周疲劳试验研究，并与疲劳寿命预测结果进行对比验证，所得结论为提高主轴的疲劳可靠性奠定基础。

1 主轴疲劳样件检测及力学性能测试

某履带车辆综合传动系统主轴在铺面路的循环工况下多次发生疲劳失效，疲劳断裂实物如图1所示，可以看出，传动主轴在右侧发生断裂。对已经产生初始裂纹的传动主轴局部进行观察(图1中红色框内)，如图2所示，发现裂纹起源于输出花键与过渡圆弧交界位置的齿根处。将主轴疲劳样件裂纹打开，宏观形貌如图3所示，可见典型的疲劳弧线，属于疲劳断裂。

图1 主轴断裂样件Fig.1 Fractured main shaft

图2 裂纹位置Fig.2 Crack location

图3 裂纹断口宏观形貌(放大倍数10)Fig.3 Macroscopic morphology of crack fracture (10×)

从主轴疲劳样件的不同方向上截取5根拉伸试样，开展力学性能的测试，结果如表1所示，可以看出，传动主轴的抗拉强度在1 807～1 930 MPa之间，屈服强度在1 521～1 642 MPa之间，断裂伸长率范围10.0%～12.6%，断面收缩率范围41.6%～49.0%，可得平均抗拉强度为1 865 MPa，平均屈服强度为1 575 MPa，平均断裂伸长率为11.5%，平均断面收缩率为46.2%.

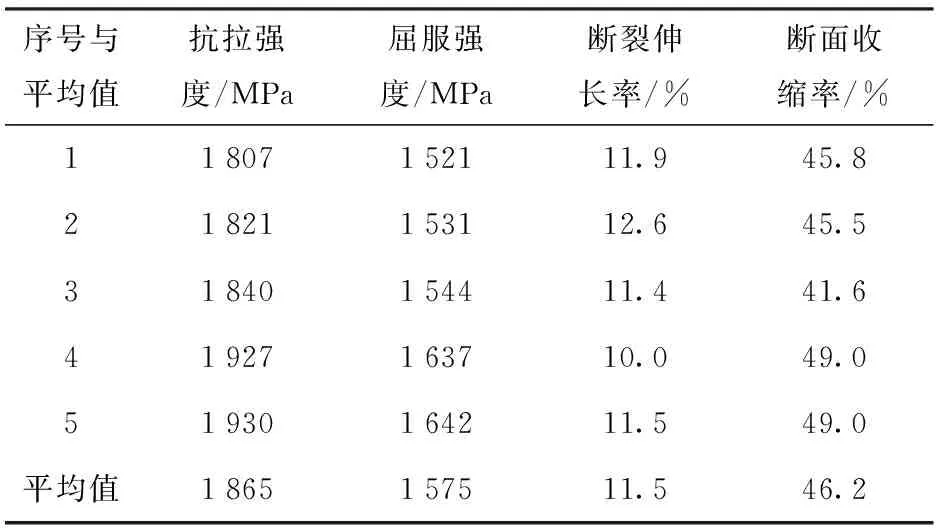
表1 力学性能测试结果

2 主轴动态扭矩测试及分析

据统计疲劳失效传动主轴的寿命里程分布范围在867～2 660 km，结合疲劳样件的失效分析，推断传动主轴属于低周疲劳失效，为确定造成主轴低周疲劳失效的行驶工况和载荷条件，开展实车动态扭矩测试。

2.1 主轴动态扭矩测试原理

综合传动系统主轴的中间渐开线花键与变速机构连接作为输入，两端的渐开线花键与汇流排连接作为输出，由于系统布局约束，主轴两侧为非对称结构。由于主轴在传动系统内部存在结构布局和空间约束的限制，难以直接测试主轴的动态扭矩，间接测量与主轴输出花键连接的汇流排输出齿轮的动态扭矩，动态扭矩的实车测试位置如图4所示。在获得汇流排输出齿轮动态扭矩的基础上，进一步除以汇流排传动比，作为主轴的实车动态扭矩。

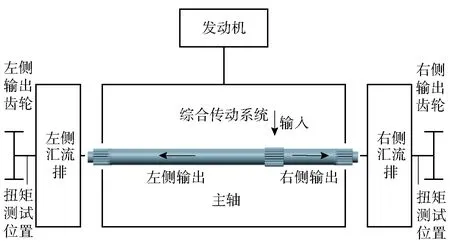
图4 动态扭矩的实车测试位置Fig.4 Dynamic torque test position of transmission

在汇流排输出齿轮内径安装嵌入式扭矩测试装置[11]，其原理和实物图如图5所示。嵌入式扭矩测试装置包含应变片、放大器、整流电源、信号发射模块、电源感应模块、车载供电电源等多种器件。应变片粘贴在汇流排输出齿轮内径上。综合传动系统外侧装电子模块，包括感应电源接收线圈、信号发射和整流器件。遥测系统接收部分安装在输出端盖上，包括供电电源、线圈和感应接收信号部分。

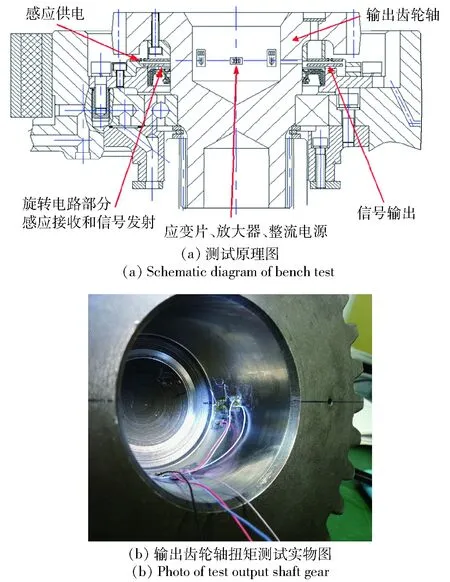
图5 嵌入式扭矩测试原理和实物图Fig.5 Embedded torque test principle and physical model

2.2 主轴动态扭矩测试数据分析

实车采集某履带车辆铺面路循环工况下汇流排输出齿轮的动态扭矩，单个循环工况包括2挡起步、2挡行驶、2挡降1挡、1挡转向和1挡降空挡，动态扭矩时域曲线如图6所示。由图6可以看出：车辆在起步阶段下存在明显的冲击扭矩，右侧冲击扭矩峰值为21 360 N·m，左侧冲击扭矩峰值为15 800 N·m；另外，在转向工况下主轴的扭矩也较大，右侧最大扭矩和左侧最大扭矩分别为8 820 N·m和6 650 N·m. 对起步阶段进行局部放大，如图7所示，可以看出，由于起步换挡过程的缓冲油压特性，造成传动系统在起步阶段存在多次冲击载荷，且冲击载荷的峰值呈递减的趋势。

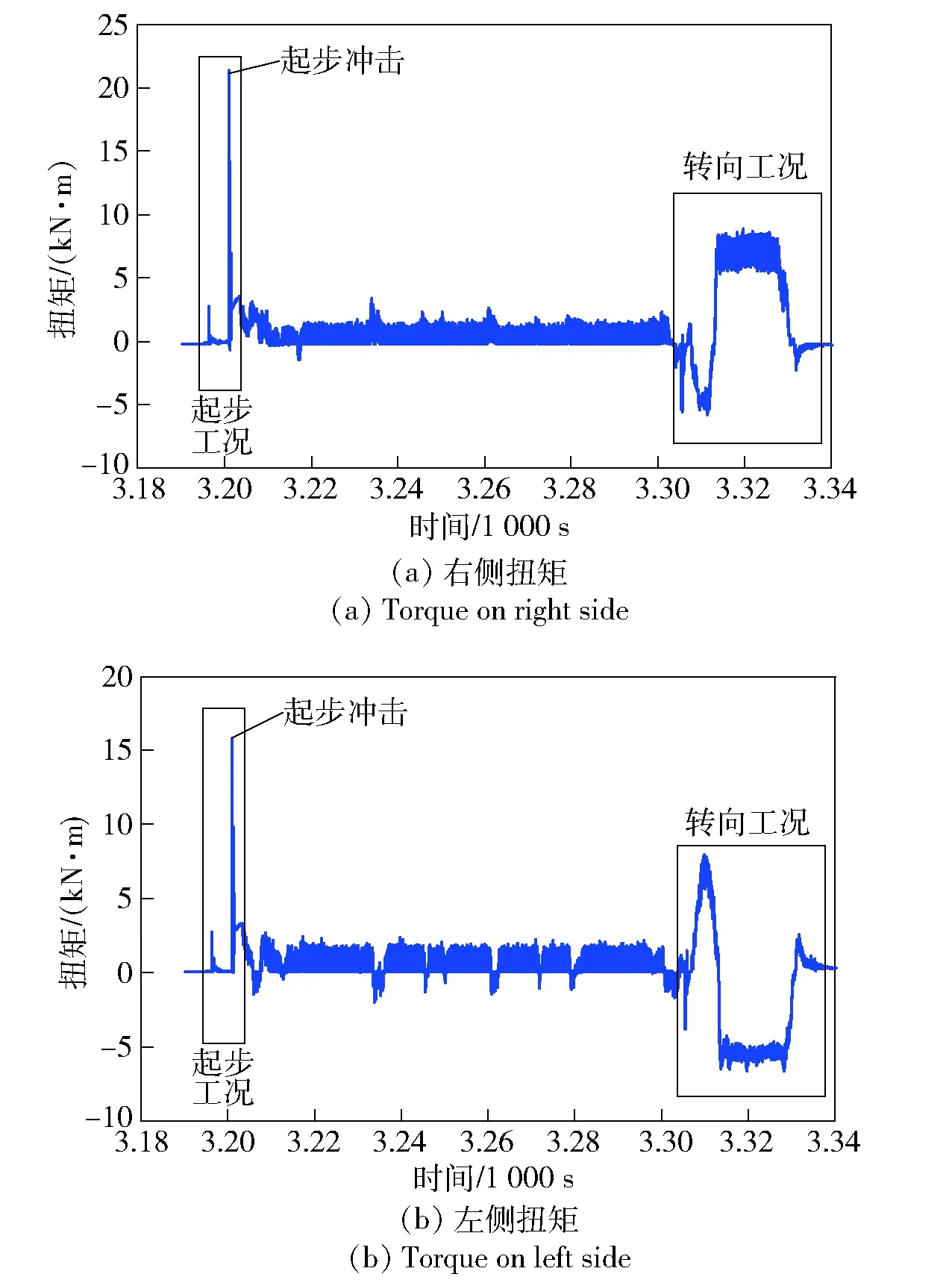
图6 动态扭矩时域曲线Fig.6 Time-domain curves of dynamic torque

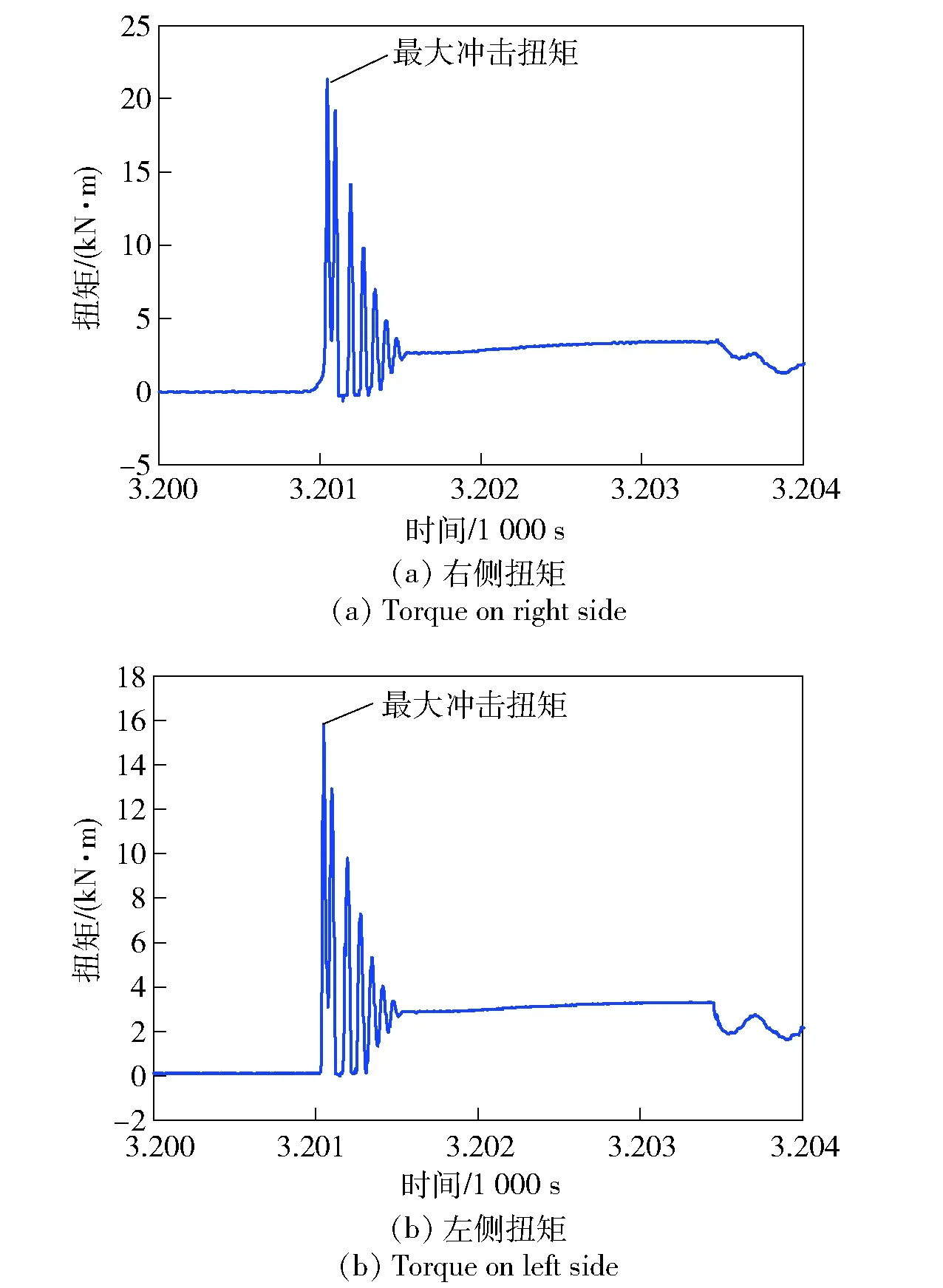
图7 动态扭矩时域曲线(局部放大图)Fig.7 Time-domain curves of dynamic torque(patial enlarged view)

采用双参数雨流计数法对右侧循环工况下实测扭矩进行统计分析，统计结果如图8所示。根据疲劳线性累计损伤理论[12]，分别计算2挡起步阶段、直驶阶段和转向阶段的主轴右侧累计损伤量及损伤比重，结果如表2所示。通过分析可确定，2挡起步阶段下的疲劳损伤最大，损伤比重高达98.41%，而直驶阶段和转向阶段损伤比重之和仅为1.59%. 另外，单个起步阶段前两次冲击的累计损伤量及损伤比重如表3所示，损伤比重之和达到98.03%. 综合上述分析，2挡起步阶段的前两次冲击扭矩是造成主轴疲劳失效的主要行驶工况和载荷条件。

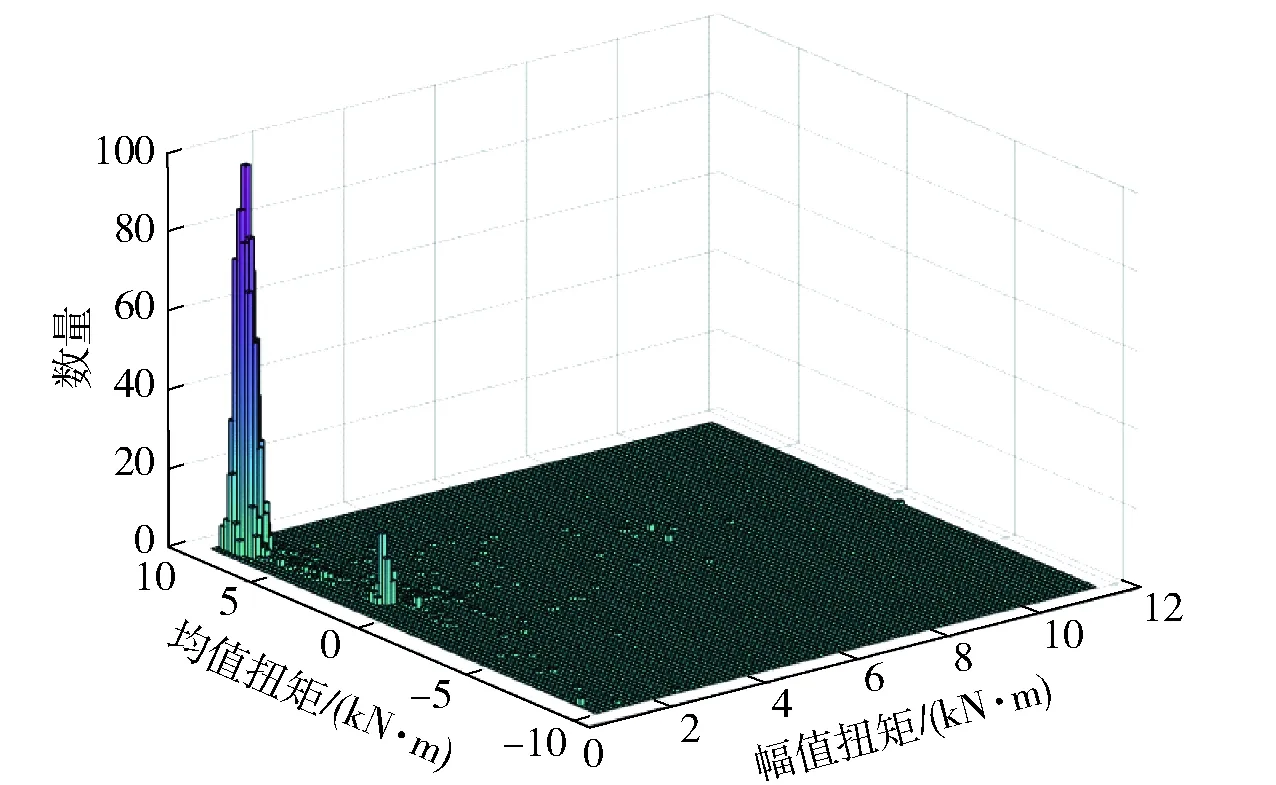
图8 循环工况下实测扭矩雨流计数图Fig.8 Counting chart of rain flow

表2 循环工况下疲劳损伤累计表

表3 单个起步阶段疲劳损伤累计表

下面重点针对损伤比重最大的2挡起步阶段输出齿轮和主轴的前两次冲击扭矩进行统计分析，部分试验数据如表4所示。据统计，左侧输出齿轮的冲击扭矩分布范围在11 500～15 800 N·m，右侧输出齿轮的冲击扭矩分布范围在18 100～24 700 N·m，冲击扭矩平均值分别为14 240 N·m和21 970 N·m. 经汇流排传动比换算，得到主轴左侧的冲击扭矩分布范围在8 327～11 441 N·m，主轴右侧冲击扭矩分布范围在13 106～17 886 N·m，两侧冲击扭矩平均值分别为10 311 N·m和15 909 N·m. 另外，由于主轴双侧非对称的结构特点，导致传动主轴右侧冲击扭矩均值为左侧的1.54倍，且主轴断裂位置同样发生在右侧，验证了测试结果的有效性。

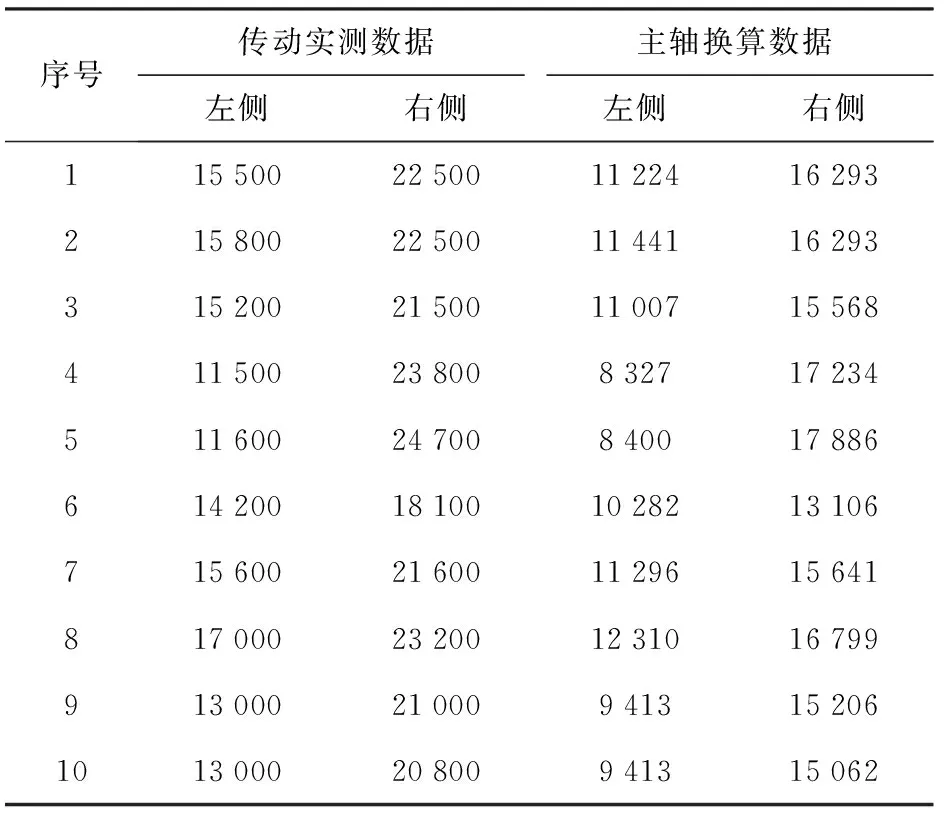
表4 起步阶段部分冲击扭矩峰值数据

3 主轴弹塑性分析及低周疲劳寿命预测

3.1 主轴材料弹塑性特性

针对传动主轴弹塑性有限元分析需要确定主轴材料的应力- 应变曲线，真应力和真应变分别由(1)式和(2)式计算：

εT=ln (1+ε)，

(1)

σT=σ(1+ε)，

(2)

式中：εT为真应变；σT为真应力；ε为工程应变；σ为工程应力。

主轴材料在屈服和缩颈之前是均匀塑性变形阶段，遵循幂乘关系硬化规律，真应力和真应变之间满足holloman公式[13]：

(3)

式中：K为循环强度系数；n为循环应变硬化系数。

对(3)式两侧取对数，得

lnσT=lnK+nlnεT.

(4)

依据lnσT和lnεT线性关系，结合主轴材料拉伸力学关系，确定lnσT和lnεT曲线上的屈服点和缩颈点，从而确定循环强度系数和循环应变硬化系数[14]，计算结果如表5所示。表5中εTX为真实屈服应变，εTU为最大真应变，σTX为真实屈服应力，σTU为最大真应力。考虑到采用多线性等向强化模型比双线性等向强化模型精度更高，在有限元模型中主轴材料的弹塑性特性采用多线性等向强化模型。

表5 循环强度系数和循环应变硬化系数

3.2 主轴弹塑性有限元仿真

为提高仿真效率，在保证仿真精度的前提下，对主轴三维模型进行合理简化，包括去除径向润滑油孔和机加中心定位孔，并将中间输入渐开线花键简化为圆柱面。基于有限元分析软件ANSYS Workbench建立传动主轴的弹塑性有限元分析模型，首先，分别针对中间圆柱面和两侧输出花键的啮合面建立3个远程点(remote point)模拟花键接触，并自动划分四面体网格，随后，采用远程位移(remote displacement)约束主轴中间圆柱面扭转自由度，并在主轴左侧和右侧输出渐开线花键的远程点(remote point)分别施加冲击扭矩均值10 311 N·m和15 909 N·m. 主轴网格模型及载荷约束条件如图9所示。

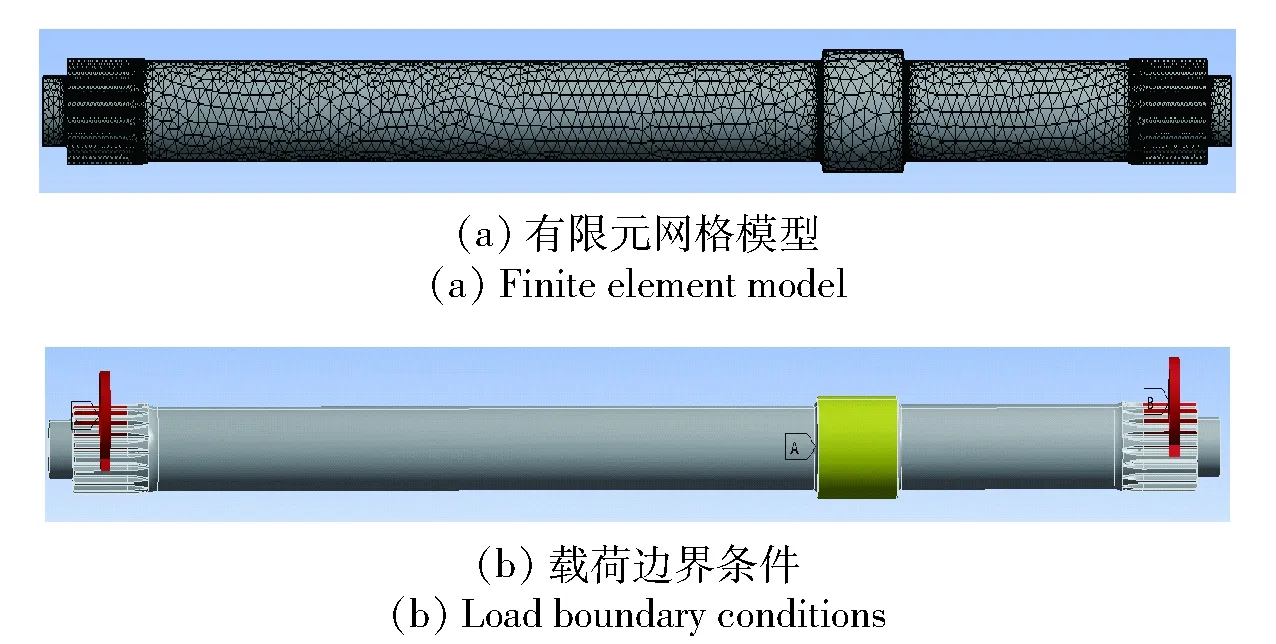
图9 主轴有限元模型及载荷边界条件Fig.9 Finite element model and load boundary conditions

主轴的弹塑性有限元仿真分析结果如图10所示，主轴的最大Mises应力为1 510 MPa，最大等效应变为0.008 693，其中弹性应变为0.007 553 9，塑性应变为0.001 167. 经对比分析，主轴的最大Mises应力接近于表1中的平均屈服强度1 575 MPa，属于低周疲劳。由局部放大图可以看出，主轴的最大应力和应变位置均发生在主轴右侧输出花键与过渡圆弧交界位置的齿根处。结合主轴疲劳断裂样件可以看出，弹塑性有限元分析的最大应力应变位置与疲劳断裂的位置一致。

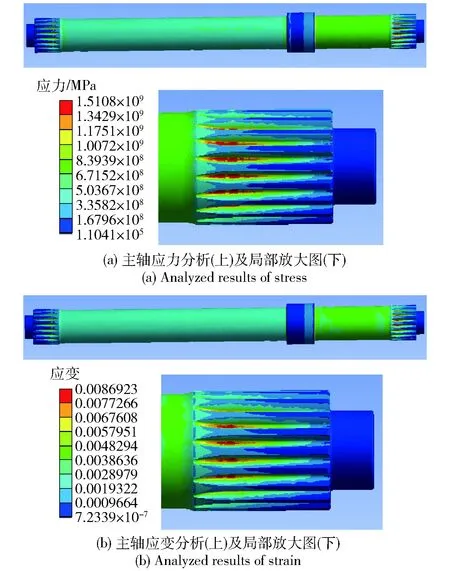
图10 主轴应力和应变分析结果Fig.10 Analyzed results of stress and strain of main shaft

3.3 主轴低周疲劳寿命预测

履带车辆起步过程中，主轴的动态扭矩变化是比值接近于0的非对称循环载荷，因此采用基于Mises屈服准则且考虑平均应力效应的Morrow修正模型对主轴的低周疲劳寿命进行预测[15]：

(5)

式中:ΔεT为总应变范围；σ′f为疲劳强度系数；σm为平均应力；E为弹性模量；Nf为循环周次；b为疲劳强度指数；c为疲劳延性指数；εTF为真断裂延性，

(6)

ψ为主轴材料断面收缩率，取值为表2中的平均值46.2%.

考虑到主轴材料的疲劳强度系数和真实断裂应力接近，因此采用真实断裂应力代替疲劳强度系数。根据拉伸断裂应力并进行修正，可计算真实断裂应力[16]为

(7)

式中：σTF为真实断裂应力；σF为拉伸断裂应力，σF=a/2R=0.88(εTF-εTU)，a为缩颈区最小截面半径，R为缩颈区轮郭线曲率半径。

基于主轴的弹塑性有限元仿真分析结果可得应变范围ΔεT=0.008 692 3，根据表2中的主轴材料检测结果可得εTF=0.619 9，根据(9)式可得疲劳强度系数σ′f=2 970.5 MPa. 将应变范围、真断裂延性和疲劳强度系数代入(7)式，得到主轴的低周疲劳寿命为17 082，即主轴承受17 082次起步冲击扭矩会产生低周疲劳裂纹。

4 主轴低周疲劳寿命试验验证

为验证2挡起步阶段主轴低周疲劳寿命预测方法的可行性，搭建综合传动系统试验台，将综合传动系统两侧汇流排输出齿轮固定在基座板上，模拟车辆的起步阶段，并实时采集综合传动系统两侧汇流排输出齿轮的扭矩，综合传动系统起步阶段模拟试验台布局如图11所示。

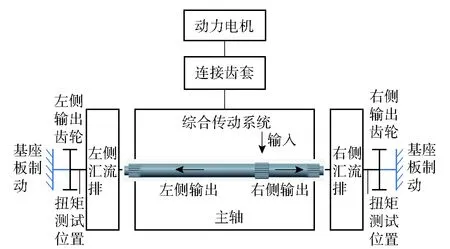
图11 综合传动系统起步阶段模拟试验台布局Fig.11 Layout of start condition test bench

综合传动系统起步阶段的动力学关系复杂，很难在台架试验之前准确地预测冲击扭矩大小，首先通过测试获得台架试验模拟起步阶段下的冲击扭矩。单个模拟起步阶段下右侧汇流排输出齿轮的冲击扭矩时域曲线如图12所示，可以看出，冲击扭矩值最大为27 250 N·m，且冲击载荷的峰值呈递减的趋势，与图7中实车冲击扭矩的变化趋势一致。结合图7(a)，可知台架试验获得的冲击扭矩比实车数据大，原因在于台架上传动系统的汇流排输出齿轮固定在基座板上，近似为刚性约束，而实车时，一方面车辆具有一定的惯性，另一方面与汇流排输出齿轮连接的零部件存在一定的柔性，能够起到缓冲作用起步阶段。起步阶段单个模拟起步阶段前两次冲击的疲劳损伤累计如表6所示，前两次冲击的损伤比重之和达到99.18%. 上述分析说明，台架试验方案模拟实车起步阶段是合理可行的。

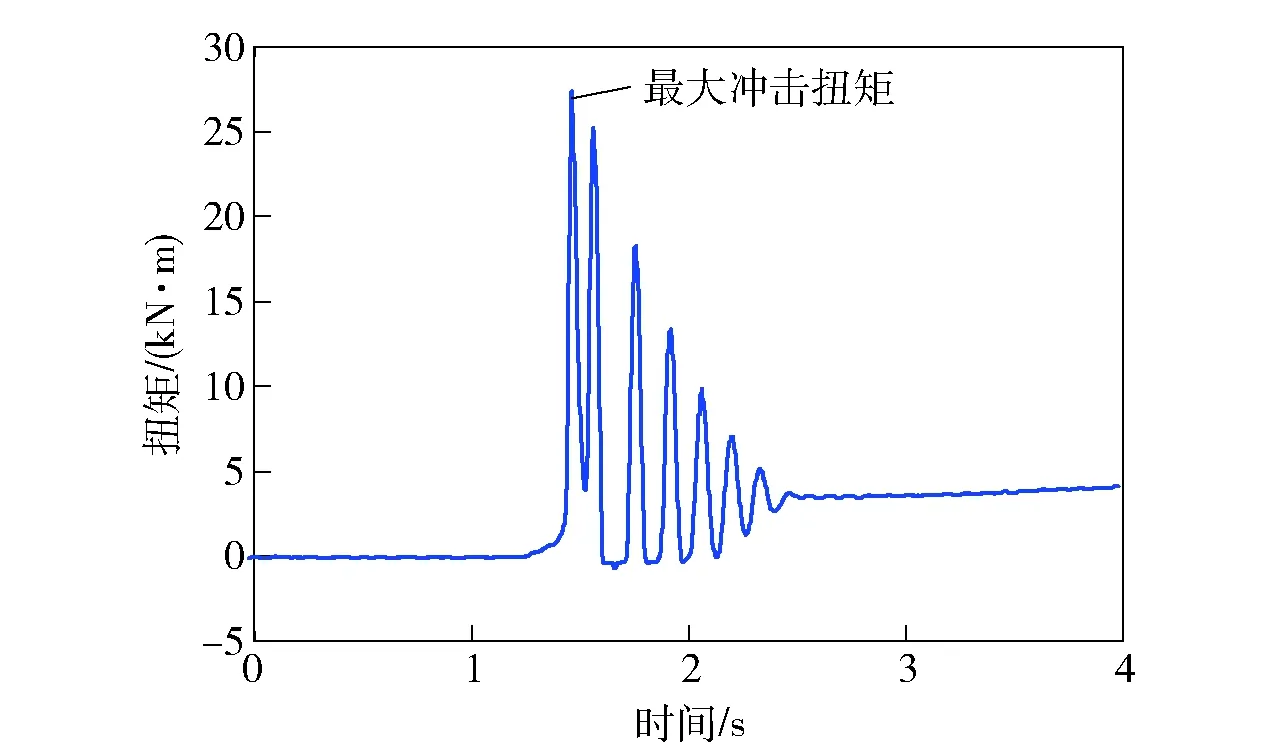
图12 单个模拟起步阶段冲击扭矩时域曲线Fig.12 Time-domain curve of impulsive torque under start condition

表6 单个模拟起步阶段疲劳损伤累计表

经过台架试验模拟多个起步阶段的扭矩测试，各起步阶段获得的冲击扭矩变化规律和幅度基本一致，主轴冲击扭矩变化范围在17 985～20 926 N·m，前两次冲击扭矩均值为19 769 N·m. 将主轴冲击扭矩平均值作为弹塑性有限元分析的载荷边界，可得主轴最大Mises应力1 610 MPa，等效应变范围为0.011 533，代入(7)式可得主轴的低周疲劳循环次数为5 843次，即主轴能承受的冲击扭矩次数为5 843次。

实车上传动主轴已经发生疲劳断裂，依据等损伤的原则，针对主轴开展疲劳试验直至产生疲劳裂纹为止。结合低周疲劳寿命预测结果，将试验分为多个阶段，每个试验阶段模拟1 250次起步阶段，结束后对综合传动系统进行分解，并采用显影剂观察主轴的裂纹情况。具体试验步骤如下所示：

1)启动输入电机将其转速升至车辆怠速转速(800±10) r/min；

2)换挡手柄置于空挡位置，液力变矩器处于解锁状态；

3)换挡手柄由空挡位置切换到起步位置，保持2～3 s，再切换回空挡位置；

4)间隔10～15 s重复步骤3；

5)每进行1 250次试验之后分解综合传动系统检查，采用显影剂对主轴进行探伤分析。

针对图13所示主轴样件开展疲劳试验，在第1次试验循环结束后，经显影剂探伤分析的主轴未发现疲劳裂纹，在第2次试验循环结束后，主轴右侧花键齿根处发现明显的疲劳裂纹，探伤结果如图14所示，结果表明在承受2 500次起步阶段下，主轴发生低周疲劳裂纹，且疲劳裂纹位置与实车结果一致。考虑到传动主轴的最终断裂寿命与裂纹萌生寿命基本相同，同时前两次冲击扭矩的疲劳损伤度最大，因此，试验所得主轴经历过5 000次冲击扭矩发生疲劳断裂，仿真结果与试验结果基本一致，验证了主轴疲劳寿命预测方法的可行性。

图13 主轴样件Fig.13 Test sample of main shaft

图14 主轴探伤结果Fig.14 Detected results of fracture of main shaft

5 结论

本文以综合传动系统主轴为研究对象，针对低周疲劳失效的问题，开展了循环工况下的主轴动态扭矩测试，获得了主轴低周疲劳失效的使用工况和载荷条件，建立了主轴的弹塑性有限元模型，并获得了主轴的低周疲劳寿命，搭建了模拟车辆起步阶段的综合传动系统试验台，依据试验结果对寿命预测结果进行了对比验证。得到主要结论如下：

1)车辆在起步阶段下的冲击扭矩是造成主轴低周疲劳的主要原因，由于主轴的双侧非对称结构，右侧冲击扭矩均值为左侧的1.54倍左右。

2)主轴最大Mises应力为1 510 MPa，最大等效应变为0.008 692 3，均发生在右侧输出花键与过渡圆弧交界位置的齿根处，与主轴疲劳断裂位置一致，且主轴所能承受的冲击扭矩次数为17 082次。

3)综合传动系统台架试验条件下主轴承受起步冲击扭矩次数5 000次，疲劳寿命预测获得主轴所能承受的起步冲击扭矩次数5 843次，仿真结果与试验结果吻合较好，验证了低周疲劳寿命预测方法的可行性，具有一定的工程应用价值。