估计点云模型的微分几何量应用探讨

王利娟

(太原科技大学 华科学院，山西 太原 030024)

在三维数字扫描仪几何获取能力持续增强的过程中，通过扫描方式数字化，使现实世界中的复杂物体转变为三维数字几何模型.使用大量的点云促进了三维模型获取、传输和存储的研究.点云微分几何量对于三维形状理解与感知尤为重要，以此实现后续几何造型与编辑.各采样点处的曲率、法向等尤为重要，法向指的是计算机图形学基本几何量，比如模型简化、曲面重建、光线跟踪等，都和法向估计具有密切关系[1].以此，对点云模型微分几何量的研究具有重要意义.

1 三阶局部拟合曲面

利用最小二乘法与邻域构造代数曲面的方法实现离散网格模型顶点微分几何属性的估算，目前，Razdan等人提出了将双二次Bezire参数曲面作为基础的拟合局部区域估算微分几何属性的方法，此方法简化了参数曲面的构造，并且设置了具备噪声的网格模型，方法中的权因子与调节矩阵能够提高拟合曲面.曲率和二阶导数具有密切关系，而且具有大量局部几何形状.因此，本文利用加权双三次Bezier曲面拟合网格顶点和邻域.

双三次Bezier曲面公式为：

公式中的Bi，3(u)，Bj，3(v)指的是Bernstein基函数，bij指的是Bezier曲面控制顶点.

本文利用双三次Bezier曲面对给定顶点pi与周围2-邻域网格顶点进行拟合，利用次拟合顶点对拟合曲面控制顶点bij进行拟合.假设参数曲面中拟合点所对应(ui，vi)参数，就要对此参数进行计算[2].

假设顶点pi邻域中的顶点有n个，所以就要对此顶点法向量实现算术平均，从而得出pi点公共法向量N.之后，创建将pi作为原点并且垂直此法向量的切平面.在此平面中创建笛卡儿坐标系，假设此平面中邻域点的投影点到原点方向为x-轴，垂直方向为y-轴.此平面中全部邻域顶点的投影点处于同一个矩形区域中，此矩形利用参数到标准[0，1]2区域中转变.此投影点坐标值也就是参数曲面拟合点参数，在投影拟合点处于此切平面的时候，假如投影点重合或者相交，使切平面原点改变，从而解决此问题.

得出顶点pi与拟合点参数(ui，vi)之后，就能够得出线性方程组Ax=B：

针对方程组Ax=B，能够得到x中全部控制顶点bij，以此得出局部拟合曲面.但是在利用最小二乘法对此方程组求解的时候，得出局部拟合曲面无效[3].为了提高局部拟合曲面精准率，可以设置调节矩阵和权因子：

为了提高局部拟合曲面的光滑度，要均匀分布双三次Bezier曲面控制顶点.通过实验结果分析，以下矩阵S为良好选择：

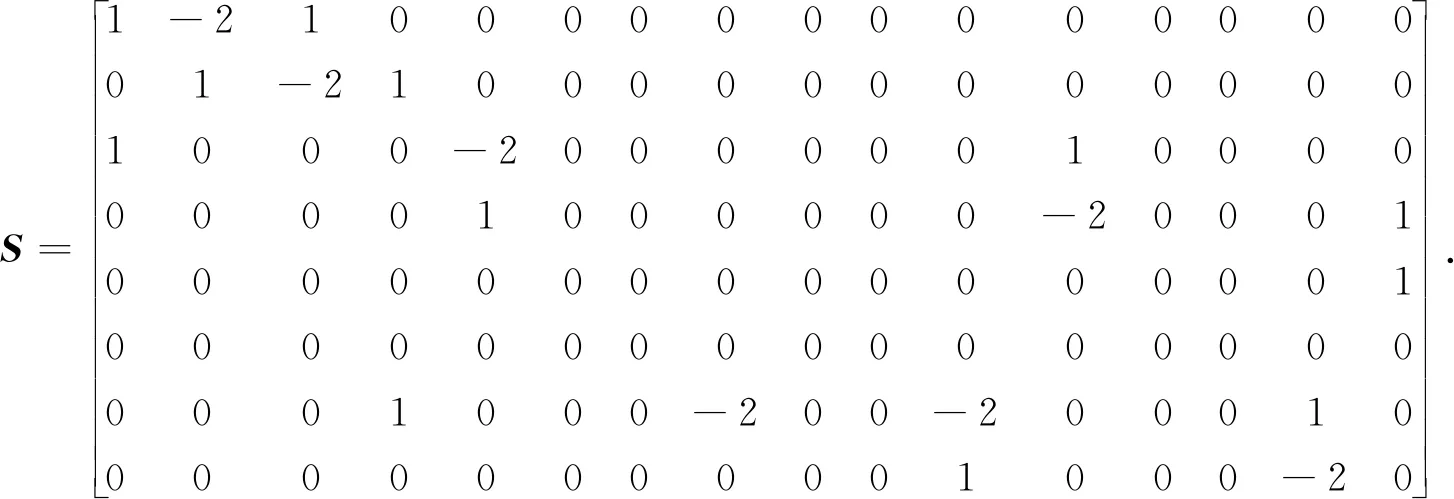
权因子α能够在[0，1]以模型噪声密度调节，在具有大量噪声的时候，α设置低值；相反，α设置高值.在缺省逼近下，使其设置为0.8.针对以上方程组，利用最小二乘法求出控制顶点，以此能够得出双三次局部拟合曲面.这个时候顶点p1就是局部拟合曲面中点B(u1，v1)，从而对顶点p1的微分几何属性进行估算[4].

2 曲面拟合与法向拟合

2.1 法向拟合

通过理算数据重新创建连续曲面，对参数曲面寻找，以此实现采样点到曲面距离最小优化与平方.通过离散曲面对曲率等二阶微分量估计，并不是局部曲面拟合.充分考虑点位置为曲面零阶微分量，法向指的是一阶微分量.利用分析可以看出来，曲面拟合方法指的是在零阶微分量中最小化采样点与曲面的差别.针对将法向误差作为主要目标函数得到最优曲面问题，也就是法向拟合.曲面二阶微分量和一阶微分量具有密切关系，因为微分计算针对噪声较为敏感，所以针对带噪声离散数据二阶微分量估计，将法向作为基础的拟合方法针对点位置来说，具有良好的性能，以下就对此方法进行说明[5].

2.2 拟合算法

分析二阶微分量，要实现两阶或者以上的多项式曲面阶次的拟合，也是使用二阶多项式曲面.本文对利用二次、三次多项式曲面实验进行拟合，将法向拟合算法QN、基于二次多项式曲面拟合算法QP、三次多项式曲面的曲面加法项拟合算法CPN、基于三次多项式曲面法向拟合算法CN等算法实现对比.对针对二次多项式曲面拟合，QP拟合曲面方程公式为：

算法QN的拟合曲面方程为：

公式中的(x，y，z)指的是拟合点在局部坐标系中的三维坐标方程，(nx，ny，nz)指的是对应点法向量，a，b，c为单估计二次多项式曲面系数约束方程表示为：

公式中的a，b，c，d，e，f，g指的是需要估计的三次多项式曲面系数[6].

2.3 实验结果

本文设计对比试验对以下情况研究，不同拟合差别为：

其一，离散数据点没有噪声，已知各个采样点处的曲面准确法向；

其二，离散数据点没有噪声，但是各个采样点中的曲面准确法向未知；

其三，离散数据点噪声明显，并且采样点曲面未知精准法向.

在圆环(R=2，r=1)与测试曲面中随机采样5 000点能够得出无噪声点云模型，也就是曲面参数方程，计算曲面中法向、曲率与主方向中精准信息，以此对不同条件下算法估计误差进行对比.为了实现不同微分量估计算法的鲁棒性，在数据合成过程中以各点法线方向中添加不同幅度Gauss噪声，噪声方差和点云数据的距离中值为0.1，0.2，…，0.9，1.图1为模型中估计平均绝对误差[7].

图1 模型中估计平均绝对误差

通过分析表示：

其一，QP算法性能最差，CN和QN性能基本相同；

其二，CPN与CN算法的性能曲线基本重合，以此表示在法向拟合过程中，新添加的点位置约束无法提高二阶微分量的估计性能.

通过此情况表示，在对点云曲面二阶微分量进行估计的过程中，法向拟合性优于点位置曲面拟合性能，数据点的噪声比较大，此表现更加明显.以此可以看出，由于法向拟合使用邻域中全部数据点法向信息，即便是法向信息并不是完全可靠.曲面拟合利用一点处的法向信息，都具有大量有效信息，可得出更加精准的结果[8].

3 点云曲率估计

以鲁棒统计学理论，离群点会对曲率估计结果造成影响.使用向前搜索算法，在进行搜索的过程中使用最小二乘中位数创建没有离群点的初始子集，两者结合在有离群点点云模型中使用.

3.1 最小二乘中位数法

本文通过LMS方法对问题求解，将其应用到曲率估计问题中.最小二乘中位数是指鲁棒回归方法，利用最小化残差绝对值中位数，对估计模型从参数鲁棒性进行估计，最小二乘和函数为中位数，使断点要求得到满足，断点使估计成为任意大非正常值需要离群点最小比例.转变成以下的目标函数[9]：

(1)

为了充分考虑点pl和点pj的距离影响，对(1)式进行改进，使用相应权值函数，那么(1)式就是：

(2)

将(2)式作为加权LMS最优化问题，第j个点残差绝对值为加权形式.

3.2 向前搜索算法和向后方法

最初DP算法为向后方法，在点云数据集合中实现任意三维点的投影计算，在之后算法迭代时，逐渐移除数据集中小权值数据点，降低参与计算点数量，使算法计算精度得到提高.但是，向后方法问题无法对点云数据中的离群点问题解决，具有比较大的离散点权值，向后无法使数据点移除，从而导致出现错误的投影计算结果.向前搜索算法的思想为：对样本集合进行选择，此子集没有离群点，作为算法开始，在迭代过程中，在计算中添加估计量样本，在达到阈值时将算法迭代结束.以此表示，算法每次迭代都没有离群点的时候实现模型参数估计，有效保证算法的鲁棒性，使估计结果的正确性得到提高.

3.3 向前搜索算法的过程

3.3.1 确定工作子集

为了降低算法处理的计算时间，使估计精度提高，针对大规模点云模型通过点云数据集合中数量小的子集，也就是工作子集，使算法效率得到提高.假设点云数据集合为CN，某采样点工作子集为cn，以权值大小选择cn中元素.对于方向投影，给出创建cn的方法[10].首先对CN中所有点权值集合{aj}计算，之后对局部变量aumic进行定义：

公式中的ktol指的是常数，amax与amean指的是权值集合最大值与平均值.对于ktol不容易控制的问题，针对权值集合{aj}实现降序排序，之后选择第n个权值作为aumic.针对n的大小，简单选择300或者在大点云规模的时候使n=N/100.本文对工作子集考虑，对采样点邻域大小确定，实现空间欧式距离考虑，实现aj的计算，所以本文也利用创建的k-d树的方法创建工作子集.

3.3.2 LMS的过程

向前搜索算法首先创建初始子集，通过最小二乘中位数法进行.k为初始子集的大小，如果选择小的k，就无法计算有效点.在k增加中，算法要大量迭代次数.假如k比较大，那么算法对于离群点比较敏感，一般使用k=p，p就是模型参数个数，p值为3.

为了避免LMS的过程中出现子集离散点，就要通过随机采样实现.首先，通过工作子集选择k点，对半径t计算，对点残差绝对值对中位数计算，重复以上过程T次，实现T个候选解生成，计算结果为最小中位数的解.根据统计学理论，LMS具有独立样本点，假设g指的是通过cn中随机采样得出的点为非离群点概率，在T次重复k个点随机选择之后，实现初始子集的选择，概率设置为P=1-(1-gk)T.为了提高P值，使用大的T值.针对每次选择k个点之后，LMS过程中使N-k个点残差进行排序，以此利用大量空间与时间.所以，创建工作子集，使内存空间与计算时间得到降低[11].

本文使用LMS方法创建初始子集Q，利用T次随机筛选，保证Q中没有离群点，在Q中将球拟合方法作为基础，计算P点曲率大小，在迭代时在Q点添加ck-Q的最小残差点，在曲率计算与上次计算达到设置阈值时终止算法[12].完整算法为：

图2 球的点云模型

1)给定云数据集与采样点，实现k-d树的创建，对pi点邻域查询，创建工作子集，对最大迭代次数、临时子集进行初始化[13].

2)以最小二乘中位数创建出示自己，对曲率进行计算.

3)在迭代处比MAXITER小的时候，使临时子集=Q，cramain=cn*Q，对cramain中全部点残差计算，在临时子集中设置最小残差，基于球拟合方法对曲率大小进行计算，设为rnew.

4)对|rnew-r|>rt进行判断.

IF：|rnew-r|

ELSE:令r=rnew，Q=ctemp，转3.

5)输出pi点曲率[14].

4 算法仿真

针对理想情况，通过球模型计算仿真.

本文使用传统方法与本文方法的实验结果详见表1.

表1 不同方法的曲率估计

本文计算点云模型采样点有3 125个，选择最大邻域为30，通过表1表示，使用传统方法所计算曲率最大值和最小值的误差为0.066 396，使用本文方法的误差为0.010 68，所以本文方法存在一定收敛性与稳定性[15].但是，在计算时间方面，本文方法要比传统方法慢，所以在实现采样点估计曲率的过程中，算法实现过程中要创建工作集，通过LMS方法创建初始子集，离散点缺少，在估计LMS算法时占据时间比较大.另外，在后续迭代的时候，在计算中添加工作集最小残差点，所以消耗时间比较大[16].本文分析方法的稳定性较高，但是算法时间比较长，所以今后就要研究计算时间和稳定性之间的平衡点.

5 结束语

基于点云模型曲率估计的问题，并且存在离群点的情况.本文通过鲁棒统计学向前搜索实现全新曲率鲁棒估计方法的设计，通过仿真结果表示，本文分析方法鲁棒性比较强，使离群点的问题得到解决.