连体并行地铁车站结构地震响应分析

韩学川, 陶连金, 刘春晓, 安 韶, 吴晓娲

(北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

随着我国经济实力的迅速发展，城市化进程的不断加快，开发利用地下空间成为建设现代化和谐都市的必要手段.按照远景规划，我国城市轨道交通运营里程将于2020年达到6 400 km，地铁逐渐成为城市生命线工程不可缺少的重要组成部分.为了满足人们的需求，地铁、广场以及商业开发相结合的一体化模式相继出现，功能较为单一的传统单体结构正逐步向共体、多体等方向发展.鉴于越来越多的复杂地下结构，如交叉、并行、穿越、连接、共建等地下结构的建设运营，其造价高，规模大，修复困难，一旦发生严重的地震破坏将造成巨大的经济损失，因此，对复杂地下结构进行抗震分析具有十分重要的意义.

目前，对大型复杂地下结构的抗震研究尚处在初步阶段，已有研究主要针对功能单一、结构形式简单的地铁车站结构、地下商业街结构等[1-3].与地上结构所处环境不同，地下结构周围土体对结构自身具有显著的约束作用[4-5]，使其很难表现出自身特性.杜修力等[6]基于ABAQUS有限元分析软件，对日本神户大开地铁车站的地震反应进行了数值计算，研究了浅埋地下车站结构的地震破坏机理.Huo[7]利用ABAQUS 通用有限元软件模拟分析了大开车站结构的震害机制；何伟[8]采用ABAQUS软件研究了二层三跨岛式地铁车站位移和结构的内力响应，模型中考虑了土体的非线性，同时考虑结构与土的接触面特性和地基无限域的影响；王国波[9]以上海地铁十号线江湾体育场站为背景，分析了地铁车站侧向连续开孔结构的地震响应规律.陈磊等[10]利用汶川地震中的近场地震动记录，研究了近场强地震动作用下地铁双层交叉隧道的三维非线性地震反应特性，并与浅埋/深埋单层隧道的地震反应特性进行了比较.张波等[11]基于有限差分软件对超近距交叉车站结构的地震响应应力、位移及加速度进行比较分析，研究了地铁交叉形式下对车站地震响应影响规律.刘晶波等[12]为研究地铁盾构隧道的地震反应特性，采用复反应分析法，研究了并行隧道间距离、衬砌厚度等因素对地震反应的影响.但这大多是针对单体地下结构或交叉结构的抗震研究，对于连体并行地铁地下车站地震响应的研究相对较少.

有鉴于此，本文以北京磁各庄站为工程背景，基于ABAQUS软件建立土-结构相互作用的三维有限元数值模型，利用典型的近、远场地震动记录，对大开洞连体并行地铁车站结构的抗震性能进行了三维非线性有限元分析，研究了不同频谱特性的地震波对结构损伤分布、变形及应力的影响.在此基础上，研究了结构侧墙不同开洞尺寸对结构地震响应规律的影响，总结了连体并行地下地铁车站结构的地震响应规律和破坏机理，以期为相似工程的抗震设计提供参考.

1 三维有限元计算模型

以北京新机场线磁各庄并行换乘地铁车站为工程背景，因远期规划与城际联络线(S6线)磁各庄站站厅换乘，负一层中间相邻侧墙开洞处理并通过地下通廊整体连接(不设变形缝)，形成一体化结构.两并行车站均为两层两跨钢筋混凝土矩形框架结构，宽22.6 m，高19.5 m，顶板覆土厚2.5 m，其中顶板厚1.0 m，底板厚1.0 m，侧墙厚0.8 m，中柱截面1.0 m×1.4 m，间距9.0 m，壁柱截面0.8 m×1.4 m，间距9.0 m.并行车站相距15 m，通廊顶板厚1.0 m，底板厚1.1 m，侧墙厚0.8 m，通廊柱截面0.8 m×1.4 m，间距9.0 m，结构主体混凝土强度采用C40，柱混凝土强度采用C50.考虑到模型计算效率及数值模拟的合理性，三维模型车站纵向取12跨，开洞位置取中间4跨且对称布置.土-地铁车站结构体系数值模型尺寸为340 m×80 m×112 m，采用八节点减缩积分实体单元(C3D8R)模拟土体介质，采用八节点全积分实体单元(C3D8)模拟车站结构.三维有限元网格划分如图1所示，模型单元总数为266 324.引入黏弹性人工边界单元[13-14]，把波动作用转换成人工边界节点作用力来实现波动的模拟.土体与地下结构之间的相互作用采用接触对的方法进行模拟，法向接触采用“硬接触”，切向接触面采用“有限滑动”，服从Coulomb摩擦定律，摩擦因数取为0.4，满足位移协调一致原则.

模型计算中，土体采用莫尔-库伦强度准则，硬化规律简化考虑为理想弹塑性，场地土层性质及力学参数详见表1.结构采用混凝土塑性损伤本构模型(CDP模型)[15]来模拟其力学行为，其物理参数详见表2.

表1 土层计算参数

表2 混凝土动力本构模型计算参数

采用具有不同频谱特性的Kobe波、Taft波和El-Centro波，总持时选取地震动前20 s.本文仅考虑水平地震动记录，假定基岩输入地震波为垂直入射的SV波，入射方向与车站纵向轴线垂直，其振动方向与结构横断面垂直，地震动的加速度时程曲线和傅氏谱如图2、3所示.Kobe波为神户海洋气象台观测点记录的近场脉冲地震波，频带相对较窄，主频率范围主要分布在0.7～3.0 Hz，低频成分丰富；Taft波为加利福尼亚州KERN县观测点记录的中远场地震波，频带相对较宽，主频率范围主要分布在0.5～6.0 Hz；El-Centro波为美国加州埃尔森特罗记录的近场地震波，频带最宽且分布相对均匀，主频率范围主要分布在0.3～15.0 Hz.3种波的主频率分布范围是逐渐加宽的.

2 计算结果与分析

在车站开洞截面与非开洞截面位置的边墙、中柱布置监测点，如图4所示，用以监测车站结构的位移、应力及加速度的变化.

2.1 地铁车站结构地震损伤及应力分析

采用损伤指数[16]描述地铁车站结构的地震损伤程度，损伤指数介于0(无损伤)和1(完全损伤)之间，通过对地铁车站结构损伤指数云图(颜色越浅损伤越大)的分析，对车站结构的损伤情况进行评估.

损伤指数可以分为局部损伤指数和整体损伤指数，局部损伤指数用来描述结构构件局部的破坏程度，整体损伤指数用来描述结构的整体破坏程度.整体损伤指数一般由局部损伤指数加权得到.针对于不同材料，拉伸和压缩都会引起损伤，因此单元损伤因子D可以以拉伸和压缩的叠加形式表达，即

D=αDt+(1-α)Dc

式中：D为损伤指数；Dt为拉伸损伤指数；Dc为压缩损伤指数；α为比例因子.

图5、6分别给出了混凝土压缩损伤指数云图和拉伸损伤指数云图.从地铁车站结构的损伤指数云图可见：

1)连体并行地铁车站结构开洞墙体的顶部和底部、洞口底部，底板与侧墙相交处，中柱的顶部、底部的拉压损伤指数明显大于其他部位，负二层(非连体层)中柱的顶部、底部损伤最为严重，是整个结构的薄弱环节.中柱的损伤比边墙大，这是由于中柱横截面积较小导致承载力相对不足造成的.

2)Taft波对结构的压缩、拉伸损伤明显大于Kobe波和El-Centro波.当输入Taft波时，车站最大拉伸损伤指数出现在底层中柱顶部，模型中塑形损伤单元数较多；当输入Kobe波和El-Centro波时，车站最大拉伸损伤出现在底层中柱底部，说明中远场地震波对结构造成的损伤最严重.这是因为Taft波的主震频率更接近结构的自振频率，结构动力响应更加明显.

3)在同一地震波作用下，车站中柱顶部和底部的压缩、拉伸损伤较大，底层中柱的损伤最为显著；车站侧墙底部与顶部受拉损伤，尤其是开洞侧墙的损伤最为严重；洞口两侧45°区域内的顶板边支座和跨中的受拉损伤较大且呈扇形分布，中板边支座、底板边支座和跨中处的受拉损伤较大；连体车站结构的受压、受拉损伤呈抛物线对称分布.这是因为车站侧墙开洞削弱了墙体和洞口两侧45°区域内结构的整体性.

4)输入相同峰值加速度(PGA)的地震波时，结构地震应力峰值(见表3)相差较大.Taft波产生的主应力值最大，El-Centro波产生的主应力值最小，这说明地震波的频谱特性对地铁车站结构的地震反应影响显著.墙体开洞位置的监测点应力幅值大于非开洞位置，而中柱监测点的应力幅值小于非开洞位置，这主要是由于侧墙开洞削弱了结构的整体性，开洞层刚度降低，结构内力重分布所导致.因此，在进行结构设计时，应适当增加开洞墙体的承载能力.

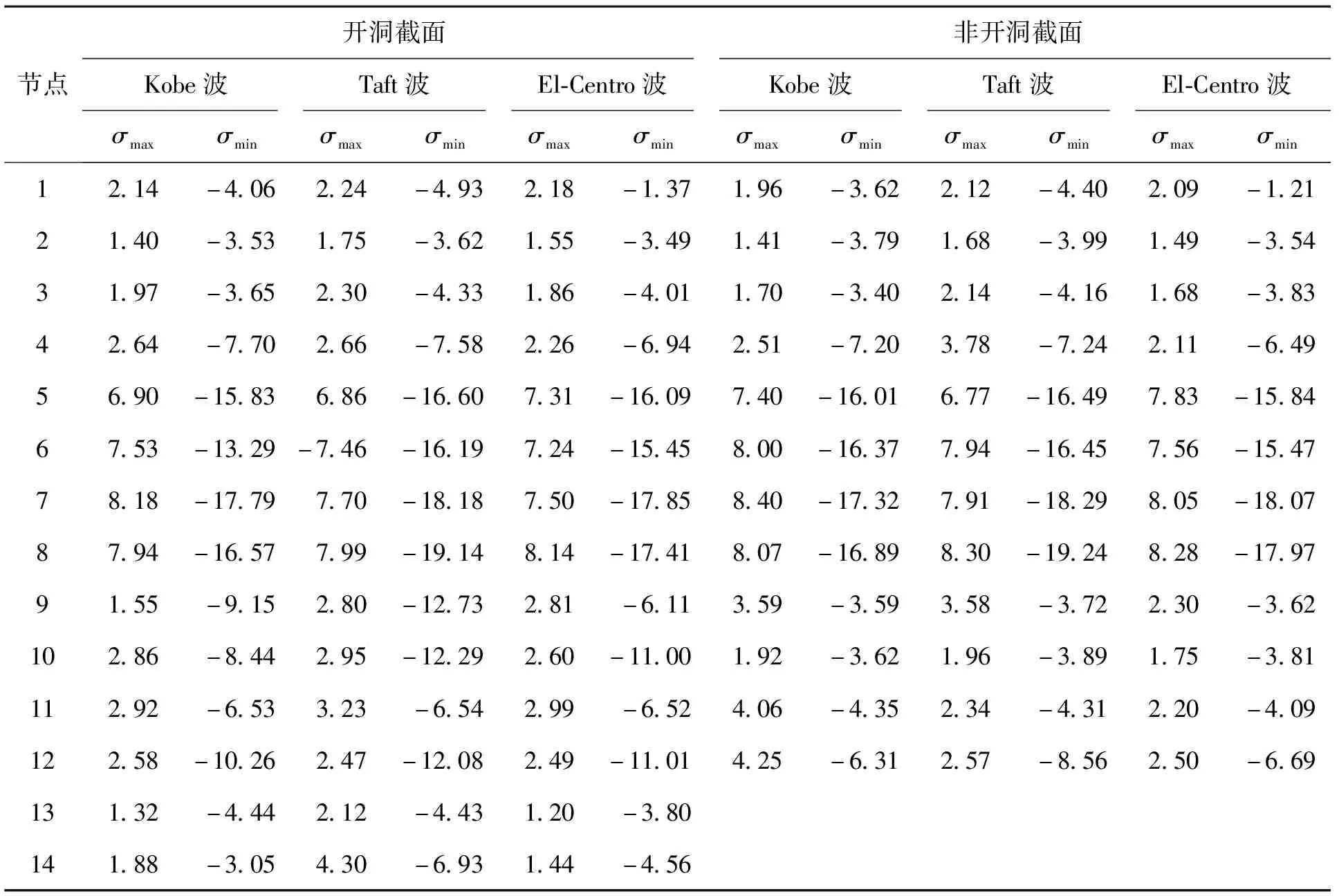
表3 连体并行地铁车站结构各关键测点应力幅值

2.2 地铁车站结构的相对位移分析

定义地铁车站结构不同深度处的水平位移幅值与结构底部水平位移幅值的差为车站结构的相对水平位移.地铁车站结构开洞与非开洞横截面边墙相对水平位移沿高度的变化曲线分别如图7、8所示.图9为地铁车站结构的最大层间相对水平位移沿纵向的变化曲线.地铁车站结构层间相对水平位移包络值见表4.可以看出：

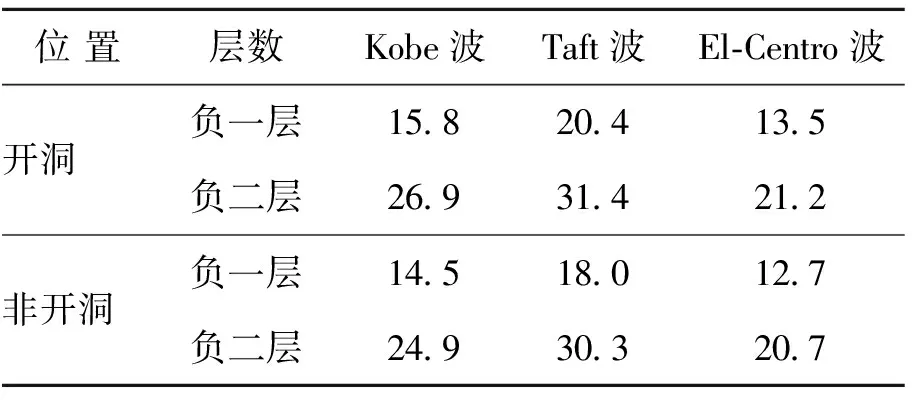
表4 层间相对位移包络值

1)开洞截面与非开洞截面边墙的相对水平位移曲线均近似呈抛物线形状，相对水平位移值基本相同，说明开洞对边墙的相对水平位移影响较小；输入Taft波时边墙左摆和右摆的相对水平位移曲线近似对称，而输入Kobe波和El-Centro波时的相对水平位移曲线偏向于一侧，这主要是因为地震波峰值加速度方向不同和土-结构的单向塑性变形累积效应所导致.

2)Taft波作用下的地铁车站层间相对位移最大，负一层中间开洞区域的相对位移值为两端的1.25～1.40倍，空间效应明显；负二层开洞区域内的层间相对水平位移峰值近似相等，说明侧墙开洞对开洞层的层间相对位移影响显著，对非开洞层的影响较小.

3)开洞位置的层间相对水平位移略大于非开洞位置，原因在于连体结构因侧墙开洞增大了车站开洞层的柔度，导致连体结构开洞层的层间相对位移增加.Taft波作用下的层间相对水平位移最大，El-Centro波作用下的层间相对水平位移最小，层间相对位移受不同地震波作用影响有较大差异.因此，结构在进行抗震分析时应该选取多条具有不同频谱特性的地震波进行验证.

2.3 地铁车站结构加速度分析

图10给出了地铁车站结构开洞截面顶、底板中点处的水平地震动加速度时程曲线.可以看出：

1)结构顶板、中板的加速度时程曲线与输入地震动加速度时程曲线波形相似，结构顶板处加速度峰值出现时刻滞后于底板，且二者均滞后于基岩处的地震动加速度峰值出现时刻.

2)Taft波作用下的加速度峰值和地震动放大系数最大，El-Centro波作用下的加速度峰值和地震动放大系数最小，这与结构损伤情况相对应.这是因为Taft波的主频与土体的基频最接近，使得放大效果更为显著；开洞位置地震动峰值加速度比非开洞位置略大一些，见表5.这是因为结构侧墙开洞导致结构局部刚度变小，自振周期变大，结构自振频率与Taft波主频率更接近.也可以看出，结构局部特性的改变对结构的地震响应影响较小，而地震波频谱特性的影响较大.

表5 结构顶板、底板中点处峰值加速度

3 影响因素分析

影响地下结构的地震动力响应有很多复杂因素，如土层性质、地震波强度、土-地下结构刚度比、行波效应等.由于篇幅有限，本节着重研究了连体并行车站结构侧墙不同开洞尺寸的地震响应规律.

结构侧墙开洞使其具有显著的空间效应，不同的开洞尺寸将影响到结构的整体刚度、自振频率、土-地下结构相互作用等方面.通过改变侧墙开洞比例(墙体开洞长度与墙体总长度的比值)来研究开洞尺寸对地铁车站结构动力响应的影响，分别计算了3种工况下连体并行地铁车站结构地震反应.其中，工况1为侧墙开洞比例1/6的连体并行车站结构；工况2为侧墙开洞比例1/3的连体并行车站结构；工况3为侧墙开洞比例2/3的连体并行车站结构.土和结构相关计算参数同上，采用具有相同地震加速度峰值的Kobe波作为基岩输入的地震波.

图11为连体并行车站结构中柱的层间位移沿纵向的变化曲线.表6为连体并行车站结构中间截面与极值截面处中柱的层间位移包络值和层间位移变化率.可以看出：

表6 层间相对位移包络值及位移变化率

1)中柱层间位移沿结构纵向的变化曲线呈正弦曲线，曲线沿中间横截面对称分布，具有明显的空间效应.3种工况相比，结构纵向两侧的各层层间位移分布趋势相同，表现为工况1最大，工况3最小；结构纵向中间区域的各层层间位移分布趋势各不相同，顶层表现为工况1最大，工况2最小，而底层表现为工况3最大，工况1最小.产生这种现象的原因主要包括两方面：第一，侧墙开洞尺寸越小，单体车站结构的整体性较强，但连体车站结构的整体性越弱，反之亦然；第二，地震波在连体并行车站之间发生了波的反射，增加了连体结构的地震响应，但随着开洞尺寸的增加，效果越小.

2)工况1、2的层间位移曲线形状相同，表现为开洞区域内的层间位移值小于洞口两侧，最小值出现在开洞区的中间位置；位移曲线从端部到洞口呈先增大后减小的趋势，最大值出现在1.2倍单体车站宽度所对应的中柱位置，这与文献[1]所得结论相似.工况3的层间位移曲线在顶层中表现为端部到洞口逐渐增大，而洞口区域表现为先减小后增大的趋势，层间位移曲线变化趋势平稳，最大值出现在中间位置，这一点与前面2种工况有显著的差别；层间位移曲线在底层中表现为端部到中间位置呈单调递增的趋势，最大值出现在中间截面位置，与顶层规律相同.这说明当开洞尺寸较小时，非开洞层层间位移显著增加，开洞层层间位移反而有所减小.这主要是因为通廊侧墙增加了结构的局部侧向刚度，从而减小了相应区域的侧向位移.随着开洞尺寸的增加，通廊侧墙的作用逐渐减小，开洞区的柔度逐渐增大，对非开洞层的约束作用减弱，层间相对位移呈先减小后增大的趋势.

3)将极值截面位移值和中间截面位移值的差与极值截面位移值的比值定义为最大层间位移变化率.可以看出，顶层的层间位移变化率随开洞尺寸的增加表现为先增大后减小的趋势，底层表现为单调递减的趋势.当开洞尺寸足够大时，各层层间位移最大变化率为0，即最大层间位移值出现在中间截面.这说明当侧墙开洞比例小于1/3时，开洞层的位移变化率最大，若将其看成平面应变问题将产生很大误差；当侧墙开洞比例大于2/3时，开洞层的位移变化率不变，可以近似看成平面应变问题.

图12给出了车站结构中间截面各关键测点应力幅值变化曲线.可以看出，3种工况下，主应力幅值变化曲线大体相同，顶层中柱的拉应力最大，底层中柱的压应力最大，是整个结构的薄弱环节.其中，非开洞墙体关键测点的应力幅值相比，工况2的拉应力最大，工况3的压应力最大；中柱关键测点的应力幅值相比，工况3的拉、压应力最大；通廊柱关键测点的应力幅值相比，工况1的拉应力最大，工况3的压应力最大.可见，应力幅值规律不太明显，主要是因为影响结构地震响应的因素较多，而不显著地表现某个因素的影响规律.

图13为车站结构中间截面顶、底板的水平向地震动加速度时程曲线.图14为车站结构中间截面顶板、底板和基岩处的水平向地震动加速度反应谱β谱.动力系数β是加速度反应谱Sa(T)与地震动最大加速度的比值，它表示地震时结构振动加速度的放大倍数.可以看出：

1)连体并行地铁车站结构顶板、底板的加速度时程曲线与输入地震动加速度时程曲线波形相似，结构顶板的加速度峰值出现时刻滞后于底板，且二者均滞后于基岩处加速度峰值出现时刻.

2)与基岩输入的地震波反应谱β谱相比，车站顶板与底板的加速度反应谱β谱明显向长周期方向移动.这与结构自振周期随结构损伤的发展而逐渐增大有关.

3)结构顶板和底板的加速度峰值基本相同.说明不同开洞尺寸对加速度峰值基本没有影响.

表7为车站结构中间截面顶板和底板的加速度峰值.可以看出：不同工况下，结构顶板和底板的加速度峰值基本相同.说明不同开洞尺寸对加速度峰值基本没有影响.

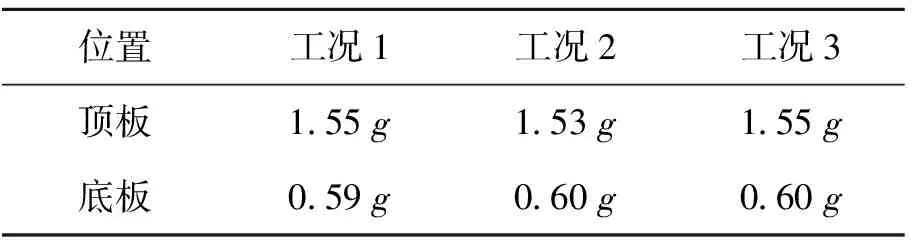
表7 结构中间截面顶板、底板峰值加速度

4 结论

1)地震动的频谱成分对连体并行地铁车站结构的地震反应及损伤有很大影响，主频率与结构自振频率接近的地震波能够对连体并行地铁车站结构造成严重损伤，甚至发生结构的塑性破坏或倒塌；连体车站结构的受压、受拉损伤呈抛物线对称分布且越靠近开洞位置损伤越严重.开洞侧墙的顶部和底部、洞口两侧45°扇形范围内结构的楼板及中柱损伤最严重，是抗震的最不利位置；开洞位置墙体的应力幅值大于非开洞位置，而中柱应力幅值小于非开洞位置，说明连体并行地铁车站空间效应明显，开洞区刚度较小，体现了连体并行地铁车站的空间效应.

2)连体并行地铁车站结构在中远场地震波作用下的层间相对水平位移最大，开洞层端部与开洞位置的层间相对水平位移相差最明显；侧墙开洞对开洞区墙体的层间相对水平位移影响较小，对中柱的层间相对水平位移影响较大.因此，应该着重加强开洞层中柱抵抗变形的能力.

3)连体并行地铁车站结构侧墙开洞比例小于1/3时，开洞层的位移变化率最大，空间效应显著，应当按空间问题进行地震反应分析；当侧墙开洞比例大于2/3时，开洞层的位移变化率不变，满足平面应变问题的基本假定，可按平面应变问题处理.