基于极值理论的核电站随机地震响应可靠性分析

秦苗珺，赵衍刚，卢朝辉

(北京工业大学建筑工程学院，北京 100124)

核电站安全壳是防止核泄漏的最后一道屏障.在基准期内核电厂可能因遭受超过设计基准的地震作用，导致结构受损并引发核泄漏等灾难性事故.因此，估计核岛结构的可靠性与定量化的安全分析对于核电工程的风险评估具有重要的意义.

按照现有相关规范[1]，一般核电厂的抗震设计主要以确定性分析为主.由于确定性的保守设计难以考虑核电厂在服役期内的诸多不确定因素，诸如地震动激励、结构材料参数、外界环境等因素导致结构抗力及响应的随机性.因此发展了基于地震概率安全评估(seismic probability safety assessment, SPSA)方法[2-3]，提出考虑内部事件和外部事件的风险评估方法.在核电结构的地震可靠性计算当中，以易损性为目标，主要采用安全系数法[4].美国先后发展了Zion方法[5]与地震安全裕度研究项目(seismic safety margin research program, SSMRP)等方法[6]，前者主要依靠主观及经验数据判断相应系数，其结果具有较大不确定性，后者未考虑参数的随机性及概率分布的特征，能力分析仍依靠经验确定.随后美国国家实验室(brookhaven national laboratory, BNL)开发了基于可靠度理论的核电结构易损性评估[7]，但由于易损性采用基于对数正态分布模型算得，难以准确反映结构失效概率的特征分布，并且该方法计算复杂，耗时较长，效率较低，不利于工程应用.近年来随着极值理论在结构工程中的应用，可根据动力可靠度理论计算结构首次超越概率[8]，而且基于结构响应极值的模拟也随之发展[9].

对于结构最大响应的分布估计仍以极值分布为主，通常采用蒙特卡洛(Monte Carlo, MC)模拟对最大反应分布的尾部进行估计[10].但由于该方法对于小失效概率结构的计算耗时庞大，效率较低，很多学者针对最大反应分布的尾部提出加速模拟方法，并对结构的最大响应进行估计.Naess等[11]对结构在随机激励下的动力系统的极值响应，采用渐进极值分布估计上穿率函数的尾部特征，从而达到加速模拟的目的.Balesdent等[12]基于Kriging代理模型采用重要抽样法得到加速模拟方法.Grigoriu等[13]提出针对动力作用下通过2种极值估计结构的可靠度的方法；He等[10]基于极值理论估计非线性振动系统的首超概率，并通过广义极值分布拟合响应极值样本的分布.

本文基于结构响应的最大反应分布估计某核电结构在随机地震下的可靠性，并采用近年来发展起来的一种高效的随机振动方法——时域显式随机模拟法[14-15]，计算实际核电结构在随机地震动下，考虑以结构顶点位移为结构的控制参数.对CAP1400型核电厂结构在随机地震激励下的最大反应分布采用加速模拟.以规范谱修改后的AP1000谱为目标谱，基于谱表示法生成对应于目标谱的随机过程.采用时域显式法计算结构在人工波作用下的时程反应，基于广义极值分布(generalized extreme value，GEV)对得到的最大反应样本拟合分布.通过加速蒙特卡洛方法估计结构在规定阈值下的失效概率.

1 数值模型及随机地震动模拟

1.1 核电站的有限元模型

某CAP1400核电站模型按照1∶1，采用壳单元与实体单元结合的ANSYS有限元软件进行建模.结构总长91.392 m，总宽为42.926 m，辅助厂房高度为47.520 m，屏蔽厂房直径为47.968 m，屏蔽厂房的高度为91.139 m，安全壳壁厚1.104 m，底板厚6.0 m.屏蔽厂房的混凝土采用C50，弹性模量Ec=3.45×104N/mm2，其中底板采用实体单元，辅助厂房与屏蔽厂房采用壳单元，其底部采用MPC约束，简化模型见图1.地震动时程采用基于规范谱改进后的AP1000反应谱生成的人工波.考查如图1(b)所示节点1处的位移.

1.2 地震动样本的生成

为保证输入模型中激励的随机性，需采用生成人工波的方法得到足够数量的地震动时程.根据随机过程理论将非平稳随机过程X(t)简化为一平稳随机过程与均匀调制函数的乘积[16]

X(t)=g(t)x(t)

(1)

式中：x(t)为零均值平稳随机过程，t为时间，按照谱表示方法可表示为

(2)

其中

ωk=kΔω，且S(ω0=0)=0

SX(ω)表示平稳随机过程的双边功率谱密度函数；g(t)为考虑地震动的非平稳性采用均匀调制函数，其表达式为

(3)

其中参数c为衰减系数，ta和tb分别为强震段的起始和终止时间，与场地类别、震中距和震级等因素相关.本文根据文献[17]中提供的数据，取ta=3 s，tb=11 s，c=0.15.

本文选用基于规范谱RG1.60修改得到的AP1000谱为目标反应谱，如图2所示.根据规范选用结构的阻尼ζ=0.05，按照SL-2级水准，采用水平峰值加速度aH=0.3g、竖向峰值加速aV=0.2g作为抗震设计基准地震动.目标反应谱取为相应峰值加速度下不同阻尼比的包络值，如图2所示.

通过功率谱与反应谱之间的关系[18]，确定目标反应谱对应的初始功率谱表达式为

(4)

式中：T为结构周期；Td为地震动持时；Sa(T)为周期为T时对应的加速度反应谱值；p为反应不超过反应谱值的概率；ω=2π/T为圆频率，ξ为结构阻尼比.

将初始功率谱代入式(2)得到相应的平稳随机过程，利用均匀调制函数得到多条地震动时程样本.求得每个时程样本下单自由度体系的加速度反应谱，对所得到的加速度反应谱处理后得到平均反应谱S′a(T)，并与目标反应谱相比，调整初始功率谱的公式为

(5)

根据式(5)，多次计算功率谱对应的平均反应谱S′a(T)，直到满足误差ε=‖S′a(T)-Sa(T)‖/‖Sa(T)‖<5%停止迭代.通过多次迭代得到平均反应谱与目标反应谱的对比如图3所示，与目标反应谱等价的功率谱如图4所示.

1.3 地震动样本数量的确定

根据功率谱与均方差之间的关系，采用均方差迭代收敛确定输入地震动样本的数量[19].依据非平稳随机过程的演化谱理论[19]，非平稳地震动时程X(t)的演变功率谱可以表示为

SX(t,ω)=|g(t)|2S(ω)

(6)

式中：S(ω)为平稳地震动的功率谱；g(t)为均匀调制函数.由演变功率谱计算得到对应的标准差时程表达式为

(7)

根据生成的地震动时程样本求得样本的标准差时程，与演化功率谱所得的标准差时程对比.其相对误差可表示为

(8)

当满足e≤ε时，输入时程的个数N即为确定所需的人工波数量，表明满足给定误差条件下生成的人工时程样本数量符合相应的功率谱.若取ε=3%，通过多次循环计算，当N≥2 400时即可满足e≤ε，两者标准差时程对比如图5所示.为考虑最大反应分布的准确估计，本文中采用N=3 000条地震动程时程样本.

2 随机地震响应分析

2.1 随机地震响应分析的时域显式法

为计算核电模型在上述地震动时程下的结构响应，本文基于近年来发展起来的一种高效随机振动方法——时域显式模拟方法.该方法可避免大量时间过程积分，在一定条件下已表明具有较高的计算精度与效率[20]，可作为实际工程中的参考方法.

时域显式方法的基本思想是通过精细积分可得到任意i时刻结构响应Ri的显式表达式[20]

Ri=Ai,0X0+Ai,1X1+Ai,2X2+…+

Ai,mXm(i=1,2,…,m)

(9)

式中：X=[X0,X1,…,Xm]为在时间向量t=[t0,t1,…,tm]下对应的地面激励，并假定激励在时间步长内是线性变化；Ai,0,Ai,1,…,Ai,m为各时刻地震激励的系数向量，反应当前时刻对后序时刻结构响应的影响.该系数向量仅与结构材料参数有关.

该系数向量可利用精细积分推导得到，也可以通过有限元软件对结构进行一次半三角脉冲分析和全三角脉冲分析获得[18].

为保证该方法在计算本文核电模型的正确性，采用时域显式方法对结构受到峰值加速度为0.3g的El-Centro波激励下进行分析，同时与采用直接瞬态时程分析的结果相对比，结点1位移Δ计算结果见图6，表明时域显式方法在该模型中有较高的计算精度，可作为该模型大量随机模拟的有效工具.

2.2 基于时域显式法的有限元分析

根据时域显式模拟法对核电结构在得到的3 000个样本时程下进行动力随机模拟.得到屏蔽厂房结构顶点位移的响应，并对3 000个响应时程样本统计前三阶矩，其中标准差时程σΔ(t)与偏度时程α3Δ(t)如图7、8所示.

从图7中可以看出，节点1 的位移响应标准差时程随时间先增大后减小，时程响应总体趋势与强度调制函数的变化趋势一致，并在峰值地震动到达时间与最大响应时间上有一定的滞后延迟.从图8所示偏度时程表明，结构响应时程是弱非高斯随机过程[21].可近似为高斯随机过程处理.

3 基于最大反应分布模型的地震响应可靠性分析

3.1 结构动力可靠度与极值理论模型

结构动力可靠性主要是衡量结构在随机动力荷载作用下的可靠度，指在规定时间内和规定条件下，完成预定功能的概率，以可靠指标为表达形式，是在概率统计上对结构安全度的定量评价.目前结构动力可靠度主要采用2种失效机制，一类是首次超越破坏机制，另一类是疲劳破坏机制[22].由于首次超越破坏机制是一个常用的简化理想模型，因此本文采用该模型给出结构动力可靠度.

对于首次超越破坏准则问题，结构在单侧界限情况下，定义结构响应Y(t)不超过安全界限b的概率.在[0,T]内的单侧动力可靠度定义为

Pr1=P{Y(t)≤b,0≤t≤T}

(10)

式中：P{·}表示随机事件的概率；b为安全范围的界限值；T为结构的设计基准期.若结构响应超过该值，认为结构处于失效状态.

本文采用单一失效准则，即核电结构顶部最大位移响应Xmax超过给定限值Δd，即表示结构整体失效，即

Pf=P{Xmax>Δd}

(11)

式中

(12)

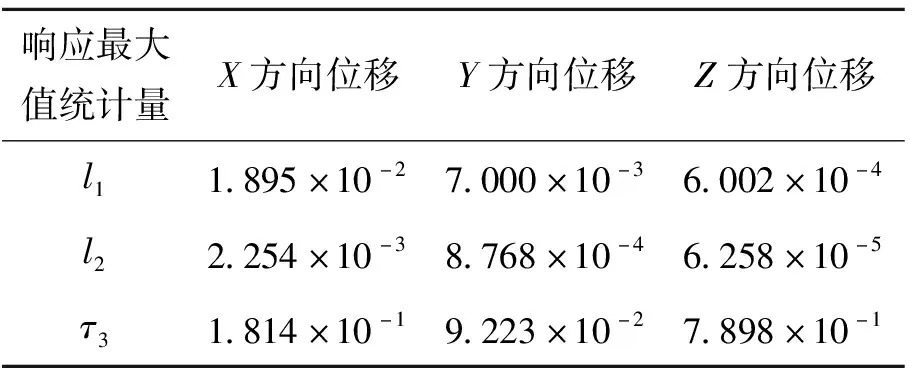
为计算式(11)中的失效概率，本文采用加速模拟的基本思想，预先假定结构最大响应Xmax服从极值分布模型.根据极值理论，结构响应的极值Xmax相应为独立同分布随机变量，则概率P((Xmax-bm)/am

(13)

式中μ、ζ、σ分别为位置参数、形状参数和尺度参数.

通过建立样本参数估计方法得到结构最大反应分布，从而按照给定限值Δd得到结构的失效概率.根据广义极值分布式(13)中核电结构失效概率为

(14)

式中：Ωθ为结构的失效域；fXmax(x)为最大位移响应Xmax分布的概率密度函数.

3.2 基于线性矩的参数估计及最大反应分布

拟合最大反应分布的精度除了取决于样本数量的大小与概率分布模型的选取，其参数估计对计算结果具有重要的影响.通常分布参数通过矩估计得到.研究表明，线性矩属于次序统计量，是按照概率权重矩的线性组合，在一定程度上较普通统计矩更有优势[23]，其主要特点是对样本序列中的极大和极小值比常规统计矩敏感性差.因此，在频率分析中，线性矩具有良好的无偏性和对最大值的稳健性.随着线性矩相对于常规矩在参数估计中的优势越来越被很多学者所接受.假设x(i)为统计样本，则样本的前三阶线性矩为

(15)

(16)

(17)

根据式(15)～(17)计算3 000个样本时程下结构最大响应值的前三阶样本线性矩，结果见表1.

表1 最大反应的前三阶线性矩

根据文献[24]所给出的线性矩与广义极值分布的参数之间的关系，得到样本的线性矩与广义极值分布参数，关系式为

(18)

通过表1所得到的样本线性矩，代入式(18)，得到广义极值分布参数，见表2.作为比较，通过普通中心矩得到广义极值分布参数见表3.

表3 广义极值分布参数的普通矩估计

表2 广义极值分布参数的线性矩估计

按照表2的分布参数，其相应概率密度函数f(x)与统计结果如图9所示.

3.3 核电结构的随机地震下的可靠度

根据文献[25]中所给的核电站易损性的超越范围，通过有限元分析确定核电站相应的Δ，按照所确定的广义极值分布计算得到相应的失效概率.当结构处于弹性状态时，即结构处于最大主拉应力超过混凝土的抗拉强度，认为结构轻微破坏；当结构的最大应变达到混凝土的峰值应变时，即认为结构处于中等破坏.由于核岛结构X方向位移响应较大，当仅考虑X方向响应时，通过PUSHOVER分析得到结构的对应的顶点位移为0.030 4 m.即当遭受到峰值加速度为0.3g地震激励时，对应混凝土开裂的概率为Pf1=1.185×10-2，相应的可靠指标为β1=2.262.当结构最大应变达到混凝土的峰值应变时对应的失效概率为Pf2=3.265×10-6，相应的可靠指标为β2=4.508.

利用普通中心矩所确定的极值分布(见表3)计算得到的混凝土开裂概率为Pf-C1=5.735×10-3，相应的可靠指标为βC1=2.528.混凝土达到峰值应变对应的失效概率为Pf-C2=1.164×10-7，对应的可靠指标为βC2=5.171.

当直接采用首超破坏计算[26]时，轻微破坏对应的概率为P′f1=8.7×10-3，可靠指标为β′1=2.378；中等破坏对应的概率为P′f2=9.25×10-7，可靠指标为β′2=4.821；相应的可靠指标为两者误差分别为ε1=4.61%与ε2=5.49%均在允许范围内.采用普通矩得到的可靠指标相对误差(ε1=6.01%与ε2=7.28%)较线性矩的大，反映了线性矩在一定程度上较普通矩有一定的优势.

4 结论

1)基于广义极值分布，提出核电站在地震作用下的最大反应分布模型，并通过线性矩匹配得到最大反应的分布参数.利用该模型便于核电站结构动力可靠度分析.

2)本文基于结构最大响应分布求解结构失效概率，评估失效概率可达10-6数量级，与蒙特卡洛方法相比，在保证一定计算精度下，可大幅缩减计算成本，提高计算效率.

3)核电结构可靠性计算结果表明，在安全停堆地震激励作用下，以轻微破坏为界，结构具有良好的可靠性，可靠指标为2.262；以中等破坏为界，结构仍具有较高的可靠度，可靠指标为4.508.此外，本文对于核电站失效模式采用单一失效准则，对于实际工程中核电结构系统多失效模式有待进一步研究.