混凝土梁中钢筋内部应变差及其与荷载的关系

刘思孟，白 煜，吴彩星

(1.省部共建山区桥梁及隧道工程国家重点实验室(重庆交通大学)，重庆 400074；2.重庆交通大学土木工程学院，重庆 400074)

钢筋混凝土结构被广泛应用于土木工程中，因此研究构件内部的变形特征具有重要的工程价值.在混凝土构件的研究、分析及设计中，常忽略钢筋内部力学响应的变化.在试验研究[1]中，混凝土中的钢筋常被视为线状杆件.对钢筋混凝土构件进行有限元分析时，通常也将钢筋简化为线单元[2-4].在荷载试验[5]等众多工程实践与试验研究中，准确测量钢筋表面的应变[6-7]是一个重要的基础.混凝土桥梁上实测的钢筋应变将用于评定结构的强度等重要性能指标[8-11].由于钢筋内部存在应变梯度，在其表面不同位置测得的应变值可能会导致评定结果发生变化.因此，钢筋内不同位置的应变差异及其变化规律课题具有重要的研究价值.

为此，本文从结构理论、有限元分析与模型试验三方面研究混凝土梁中同一根钢筋上、下缘(即顶面与底面)应变差及其与荷载的关系.研究发现：在加载过程中，上述应变差显著增大；在钢筋屈服前，受压钢筋上、下缘实测应变差之比可高达50%.因此，混凝土结构应变测量过程中，钢筋直径的影响应充分重视.

1 理论分析

1.1 基本假设

在理论研究与有限元模型分析中采用以下基本假设：

1)平截面假定.

2)小变形假定.

3)钢筋与混凝土具有良好的黏结性能，不会发生较大的相对滑移.

国内外试验表明[12]：钢筋混凝土受弯构件加载过程中，构件上的平均应变都能较好地符合平截面假定，即混凝土梁受力后正截面上混凝土与纵向受力钢筋的平均应变呈线性分布.另外，在混凝土截面的受拉区，由于开裂截面上钢筋与混凝土之间发生相对滑移，因此上述的假设有效性可能会降低.

1.2 混凝土梁中钢筋表面上、下缘应变差

1.2.1 钢筋混凝土梁截面上的应变分布

由上述假定可得，在受力过程中钢筋混凝土梁截面上的应变分布如图1(a)所示.定义坐标系后，可建立任意高度x处的应变ε与截面曲率θ、受压区高度xc之间的关系式为

ε=(x-xc)tanθ≈(x-xc)·θ

(1)

1.2.2 钢筋上、下缘应变差值的表达式

将钢筋上、下边缘的坐标代入式(1)可得钢筋的顶面和底面的应变.例如，对于受拉钢筋，上缘应变为

εsu=[(h-a′s)-d-xc]·θ

(2)

下缘应变为

εsd=[(h-as)-xc]·θ

(3)

由此可得钢筋上、下缘应变差为

Δεs=εsd-εsu=θ·d

(4)

式中：d为钢筋的直径；h为截面高度；as为受拉钢筋的保护层厚度；a′s为受压钢筋的保护层厚度.式(4)表明：钢筋上、下缘应变差Δεs，取决于截面处中性轴的曲率θ与钢筋直径d.为定量分析Δεs，需给出θ的算法.

1.3 θ的计算方法

基于纤维模型[6]，引入以下算法计算混凝土梁截面处中性轴的θ.沿截面高度方向，将整个截面分割为n条水平条带，如图2(a)所示.加载过程中，假设θ或xc的数值.首先，如图2(b)所示，根据平截面假定，计算截面第i(i=1,2,3,…)条带中心和钢筋形心的应变为

式中：εci为中心坐标为xi的混凝土条带中心的应变；εs为钢筋形心的应变.再利用钢筋和混凝土的本构方程[13-14]计算混凝土条带和钢筋的应力.

钢筋应力：

σs(εs)=E·εs

(5)

混凝土应力：

当0<εci<ε0时

(6)

当ε0<εci<εcu时

(7)

式中：σs和σci分别为钢筋和混凝土的应力；E为钢筋的弹性模量；εcu和ε0分别为混凝土的极限压应变和峰值应变；fcd为混凝土的轴心抗压强度.其次，计算钢筋的拉力和混凝土的压力

(8)

FsT=σs(εs)·As

(9)

FsC=σs(εs)·A′s

(10)

式中:h为截面上划分的条带的高度(截面均等划分)，如图2(a)所示；As为受拉钢筋截面面积；A′s为受压钢筋截面面积；FC为混凝土提供的抗力；FsC和FsT分别为受压钢筋和受拉钢筋提供的抗力.再次，利用截面上力的平衡条件[5,12-16]，建立方程

FC-FsT+FsC=0

(11)

最后，通过迭代方法搜索混凝土xc和θ的值.上述计算流程如图3所示.

采用图3所述算法得到加载过程中钢筋混凝土梁截面在中性轴处的θ后，再由式(4)计算钢筋上、下缘的应变差.另外，对于复杂的截面形状与配筋情况，可采用商业有限元软件计算θ.

2 模型试验

2.1 试件制作

为研究在加载过程中钢筋混凝土(reinforce concrete，RC)梁中钢筋顶面、底面的应变差与荷载的关系，开展了钢筋混凝土梁模型试验.梁的截面为矩形，宽为150 mm，高为250 mm，净跨径为1 700 mm.直径为16 mm的钢筋(N1)作为受拉钢筋，直径为12 mm的钢筋(N2)用作受压钢筋.设计混凝土强度等级为C35(见图4).

2.2 测点布置与加载方案

在梁的每根钢筋跨中截面的顶部和底部各布置1片应变片，见图5，沿梁轴向的八等分净跨径的9个截面底面布置9个位移传感器.

加载过程中RC梁处于四点弯曲状态，加载速率为0.005 mm/s，详细的加载方案如图6所示(由于实际荷载在加载过程中存在3个异常的点，将该3个荷载点所对应的数据剔除，故图6中出现了3个平台).

3 讨论与分析

围绕实测数据, 从以下几个方面进行了讨论：

1)钢筋上、下缘应变荷载随时间变化趋势.

2)钢筋上、下缘应变差与荷载的关系.

3)受压钢筋应变差和受拉钢筋应变差与荷载变化规律的对比及其分析.

3.1 混凝土试验梁的失效特征

加载过程中，结构的响应主要分为3个阶段: 弹性阶段(即从图7中的0点到a点)、工作阶段(从a点到b点)和失效阶段(从b点到c点).破坏时加载点附近的混凝土被压碎,导致梁发生弯曲破坏.上述特征与典型的混凝土梁的失效特征相同.

3.2 钢筋上、下缘应变随荷载变化的趋势

图8展示了钢筋屈服前2号钢筋的应变与荷载随时间的变化.可以看出，加载过程中荷载-时间、钢筋应变-时间曲线的变化趋势吻合.例如，在600～1 000 s、2 300～3 400 s、6 300～7 300 s这3个时间段里，荷载的曲线出现了较长的平台，同时钢筋上、下缘应变也出现了较长的平台.

另一方面，由式(2)(3)可知：εsu、εsd与h、as、a′s、d、θ、xc有关.在这些参数中，只有θ和xc为变量.由1.3节可知，θ与荷载有关.将试件数据代入1.3节的算法，得如图9所示曲率及混凝土受压区高度与荷载效应(即截面所受弯矩)的关系曲线.

该图表明：θ随着荷载的增加而增加，混凝土受压区高度随着荷载的增加而减小，即中和轴逐渐上移.因此，从理论上讲，图8中的钢筋应变与荷载的变化趋势是一致的.

由上述对比与分析可知：从试验梁内钢筋上测得的应变是荷载作用下该结构行为的真实反应.因此，基于这些数据来分析钢筋上、下缘应变差与荷载之间的联系是合适的.

3.3 钢筋上、下缘应变差与荷载的关系

为了分析钢筋上、下缘的应变差随荷载变化的规律，从试验数据中提取部分数据.以2号钢筋为例，从图8中提取出每个加载步中荷载峰值对应的钢筋应变，再计算钢筋上、下缘的应变差.最终，以荷载为横坐标、应变差为纵坐标，将数据点绘在图上，由此得到图10中的红线.同理，可得1号钢筋的应变差-荷载关系.

如图10所示，荷载从0增加到32 kN过程中(对应图7中的弹性阶段0a)，受压钢筋上、下缘应变差与荷载关系的曲线较为平缓，且两者间的差异较小.当荷载为32～215 kN时(即图7中的ab段，带裂缝状态)，应变差与荷载关系曲线较为陡峭，则两者差异较大.这表明：在整个加载过程中，受压钢筋上、下缘的应变差与荷载呈正相关.

由式(4)可知，钢筋上、下缘的应变差与其直径和截面曲率有关.对某一根钢筋，直径为定值；第1.3节所示的算法及分析结果(见图10)都表明：构件承受荷载越大截面处的曲率也越大.因此，随着荷载的增加，钢筋上、下缘应变差也逐渐增加，即图10所示与前面的理论分析结果一致.

3.4 受压钢筋与受拉钢筋应变差变化规律及其对比

图11、12显示在试件加载过程中钢筋的应变差比率随荷载的变化.此处，定义受压钢筋应变差比率为

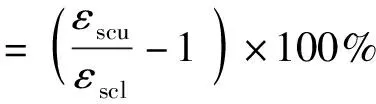
受拉钢筋应变差比率为

式中：εscu和εscl分别为受压钢筋上、下缘的实测应变值，εstu和εstl分别为受拉钢筋上、下缘的实测应变值.

如图11所示，荷载从15 kN增长到80 kN过程中，受压钢筋应变差比率变化都较为显著；在80 kN之后，2号钢筋的应变差比率呈平稳发展的态势，1号钢筋的比率呈缓慢上升趋势，两者逐渐接近，在200 kN之后两者同时逐渐上升，应变差比率随着荷载增加总体上趋于稳定.综上所述，受压钢筋的应变差比率基本同步增长.更为重要的，该图表明：即使是同一根受压钢筋，在加载过程中上、下缘的应变差比率可高达50%.

与图11相对，图12显示加载过程中受拉钢筋的应变差百分比的变化.从中可知：加载过程中，受拉钢筋上、下缘应变差百分比波动较大；随着荷载的增加，应变差最初迅速增加之后迅速减小最后趋于平稳，这与上述理论分析中所得的结论不同.同时，对比图11、12可以发现：受压钢筋上、下缘应变差与受拉钢筋上、下缘应变差和荷载的相关关系有所不同，受压钢筋应变差比率的变化要比受拉钢筋的更为稳定、清晰.

通过分析钢筋混凝土构件加载过程以及钢筋和混凝土应变的变化规律，作者认为：上述现象是由于受拉区混凝土出现裂缝且损伤较严重，使得受拉区的应变分布不再符合平截面假定.众所周知，混凝土材料是一种抗拉能力很弱的材料.构件受力后，受拉区混凝土由于达到极限拉应变而很快开裂，受拉钢筋承担绝大部分的拉应力；随着裂缝进一步扩展、上移，截面的中性轴向受压区延伸，受拉钢筋应变迅速增大、受拉区混凝土的整体性继续被削弱；当荷载变得更大，受拉钢筋与混凝土发生相对滑移，导致受拉区的变形与平截面假定有显著的偏离，使受拉钢筋应变差的演化与前述理论模型出现较大的偏差.也就是说，局部的应变分布与理想状态下的线性分布很不同，受拉钢筋上、下缘的应变之差逐渐缩小.随着荷载的增加，受拉钢筋最终达到屈服强度，应变趋于稳定.因此，出现了图12中应变比率突变之后逐渐趋于稳定的现象.

与之相反，在钢筋屈服前，受压区混凝土与钢筋之间能够维持有效的黏结；同时，由于混凝土的抗压强度较高，使得受压区混凝土能保持完整.这些因素有利于受压钢筋上、下缘应变差的稳定发展，并保持与荷载增长的同步性.

4 结论

为研究混凝土梁中钢筋应变差与荷载的关系，本文开展了理论研究与试验分析，得到了以下主要结论：

1)本文的理论研究表明，该应变差与截面中性轴处曲率呈线性关系；有限元模型计算显示，该曲率与施加的荷载成正比.

2)分析模型试验数据发现，随着荷载增长，受压区钢筋上、下缘应变差明显增长，两者基本保持线性关系.

3)在钢筋混凝土梁试件中，同一根钢筋上缘和下缘应变之差随荷载增大而增大，两者相差可高达50%.

上述研究表明：在混凝土结构的应变测量中，应充分重视钢筋尺寸的影响.在科学研究中，应重视钢筋的三维尺寸对理论研究与模型分析的潜在影响；在荷载试验等工程实践中，应充分考虑钢筋表面不同部位测得的应变数据对结构性能评定结论等的影响.