Effective control allocation using hierarchical multi-objective optimization for multi-phase flight

Liguo SUN, Qing ZHOU, Boxu JIA, Wenqin TAN,*, Hngxu LI

a School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

b Shanghai Aircraft Design and Research Institute, Commercial Aircraft Corporation of China Ltd., Shanghai 201210, China

KEYWORDS Adaptive control;Control allocation;Flying-wing aircraft;Multi-phase and multiobjective;Real-time optimization

Abstract For different flight phases in an overall flight mission, different control and allocation preferences should be pursued considering lift, drag or maneuverability characteristics. The multi-objective flight control allocation problem for a multi-phase flight mission is studied. For an overall flight mission, different flight phases namely climbing, cruise, maneuver and gliding phases are defined. Firstly, a multi-objective control allocation problem considering drag, lift or control energy preference is constructed. Secondly,considering different control preferences at different flight phases, the analytic hierarchical process method is used to construct a comprehensive performance index from different objectives such as lift or drag preferences. The active set based dynamic programming optimization method is used to solve the real-time optimization problem.For the validation, the Innovative Control Effector (ICE) tailless aircraft nonlinear model and the angular acceleration measurements based adaptive Incremental Backstepping (IBKS) are used to construct the validation platform. Finally, an overall flight mission is simulated to demonstrate the efficiency of the proposed multi-phase and multi-objective flight control allocation method.The results show that the comprehensive performance index for different phases, which are determined from the Analytic Hierarchy Process (AHP) method, can suitably satisfy the preference requirements for different flight phases.

1. Introduction

Modern aircraft tend to have good stealth and maneuvering capability due to the novel airframe configuration design and the multiple types of redundant control effectors ranging from conventional control surfaces, thrust vectors to active airflow controls.1-5The control effectors of modern aircraft usually demonstrate highly nonlinear and serious couplings characteristics.4-6Besides, it is very common for modern aircraft that the designer may make a trade between several different aspects in control performance. For example, in order to gain a high-level maneuverability,the aircraft may have to sacrifice the static stability. Similarly, a tailless aircraft configuration design is helpful to increase the lift and the stealth property,but its yawing control performance is poor and the pitching control becomes difficult.In addition,aircraft need to perform different flight tasks in an overall flight mission.Therefore,the design of a qualified flight control system is particularly important to ensure the success and safety of performing various tasks. In general, the flight control system mainly includes two parts: controller and control allocation unit. Advanced flight control laws have been intensively investigated.Adaptive nonlinear flight control methods such as model-based nonlinear dynamic inversion or acceleration measurements-based incremental backstepping are two of the promising candidates for the controller design.7-12Considering the abovementioned control effector redundancy, multi-axis couplings, effector interactions and control preference in different channels, the control allocation module plays a crucial role in extracting and enhancing the potential maneuverability or fault accommodation performance of modern aircraft.13-16

Many different control allocation methods exist in the literature. Conventional control allocation methods include redistributed weighted pseudo-inverse,17daisy chaining,18,19direct allocation method20,21and numerical optimization based allocation methods such as linear programming13,22and quadratic programming.6,23,24The optimization based allocation methods are able to take into account multiple time-varying constraints and give the designer the flexibility to choose apt cost functions.Specifically,the quadratic programming allocation method with the active set algorithms is able to efficiently solve a constrained nonlinear control allocation problem in real time.25,26

An overall flight mission consists of multiple flight phases,and different control allocation strategies are preferable for different flight phases considering the required specific flight performance of the controlled aircraft.13,27,28The existing researches on aircraft control allocation are mainly focused on multi-objective control allocation problems.6,13It is lack of research on multi-phase and coordinate allocation problems,e.g.,climbing phase,cruise phase,landing phase,maneuvering phase, etc. Besides the moment distribution accuracy,an additional performance index, e.g., the need to increase lift or to reduce fuel consumption, may usually be considered for different flight phases. Conventional flight tasks include takeoff, approach, cruise, ground attack, air combat, penetration,terrain tracking, climbing, landing and so on.

For each single flight phase, researches in the existing literature are focused on single optimization index based control allocation, e.g., energy consumption and moment allocation accuracy are considered. However, choosing a single index is usually unreasonable from the flying capability and the control preference point of view.For example,in order to prevent collision in the landing phase,we cannot blindly increase the drag for descending without considering the lift changes, and it is usually necessary to increase the lift before landing.Therefore,it is reasonable to consider the optimization index in a synthetic way,where different performance indices should be considered.Correspondingly, the weights for the abovementioned performance indices should be chosen based on the flying capability, task preference and the expert knowledge of the flight controller designer.

A novel and effective multi-phase and multi-objective flight control allocation strategy with the optimization problem architecture and optimization solver is developed for an overall flight mission of modern aircraft.In this paper,a hierarchical optimization model is proposed to deal with the multiphase character of the control allocation problem considering the different control specifications at each phase.For each different phase, a consecutive multi-objective control allocation problem is constructed in this paper, and a comprehensive optimization index is proposed to consider the priority of different performance indices. Finally, an active set based optimization method is used to solve the control allocation problem in real time, and an overall flight mission including climbing, cruise, maneuver and gliding phases is performed.The major contributions are summarized as follows:

(1) For each different phase, a comprehensive performance index based multi-objective control allocation problem is constructed, and then the Analytic Hierarchy Process(AHP) method29,30is used to determine the weights for each index. The existing researches are mainly focused on single optimization index, e.g., minimum drag, maximum drag or maximum lift.

(2) A hierarchical optimization model is proposed for the multi-phase and multi-objective control allocation, i.e.,optimization problem, in an overall flight mission. The control allocation problems for different phases are integrated. The existing studies on control allocation are mainly focused on single-phase control allocation problems.28,31

(3) The active set method based real-time incremental control allocation approach is developed, and a task chain containing four different phases is designed for an Innovative Control Effector(ICE)flying-wing aircraft to validate the proposed method.

This paper is organized as follows. In Section 2, the problem of multi-phase and multi-objective control allocation is introduced. In Section 3, the index synthesizing method is designed to solve the multi-phase and multi-objective control allocation problem.In Section 4,the simulation model is introduced to validate the proposed method. Section 5 concludes this paper.

2. Problem statement

This section firstly introduces the physical background of multi-objective control allocation for flying-wing aircraft.And then the problem is formulated into a standard mathematical optimization problem.

2.1. Problem statement of multi-phase and multi-objective control allocation

There exist many flying tasks for flying-wing aircraft in the air,and different flying tasks have different requirements.Therefore, it is necessary to analyze the requirements of control allocation for each task. An overall flight mission can be synthesized from basic tasks,so a multi-phase task chain needs to be designed first in order to investigate the control allocation problem for the entire flight mission.The basic tasks considered in this paper include climbing, cruise, maneuver and gliding. Longitudinal maneuvering is mainly considered in the maneuvering section because the flying-wing aircraft has insufficient longitudinal maneuverability since it has a backward center of gravity and no traditional elevator. The designed task chain is shown in Fig. 1, and the corresponding phase description is given in Table 1.

There are different requirements for control allocation in different tasks of aircraft,and these requirements are reflected in different performance indices,such as drag index,lift index,surface deflection index,etc.That is to say,for a specific flight phase,the multi-objective index Jk(k=1,2,3,4)should usually consider control energy cost,drag or lift preference, and command tracking precision. For different phases, Jkis different due to different preference. For example, in the climbing phase, it is necessary to increase lift and reduce drag as much as possible.In the cruise phase,it is necessary to reduce surface deflection and drag to reduce fuel consumption while the demand for lift is relatively small. In the longitudinal maneuver phase, it is also necessary to reduce drag and increase lift.In the gliding phase,increasing lift is necessary in order to prevent collision. The above-mentioned information reflects the importance of different optimization objectives in the specific task. The designed task chain for the whole process includes several different tasks;the control allocation problem for each of these phases is a multi-objective comprehensive problem,and the optimization index is considered synthetically in the cost function.

2.2. Multi-phase and multi-objective control allocation strategy

Aircraft usually carry out multiple missions in the air, which brings about the multi-phase and multi-objective control allocation problem. The overall control method is described in Fig. 2.

In Fig. 2, the flight mission unit consists of different task modes. Different performance indices would be assigned to different task modes, and then integrated indices are formed in the control allocation unit for the overall flight mission.

In this way, a series of different flight tasks can be accomplished consistently for aircraft operating in the air. Multiphase and multi-objective control allocation is to propose different control allocation objectives according to different task requirements, so that it can adapt to different tasks and improve the tracking precision in completing given tasks.The multi-objective synthesis problem associated with control allocation issue in each phase is one of the key problems to be solved in this paper.

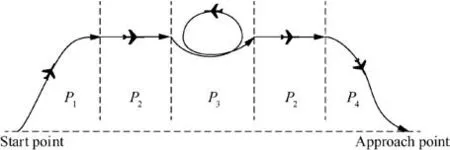
Fig. 1 Designed task chain for an overall flight mission.

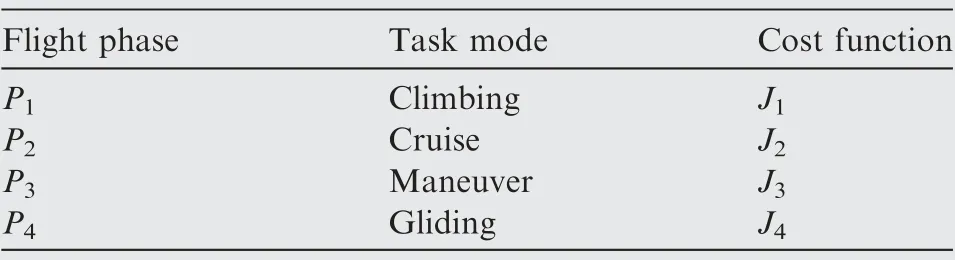
Table 1 Flight phases and corresponding cost functions in control allocation.

2.3. Modelling of multi-objective control allocation

The increase in the number of control surfaces of flying-wing aircraft brings about redundant control capability, which can improve the flying performance of the aircraft. However, the input redundancy will inevitably result in the requirement on optimal control allocation.

2.3.1. Basic control allocation problem

The basic control allocation problems are defined as follows(see Eq.(1)):under given position and rate constraints,the following equations are solved:

2.3.2. Multi-objective control allocation problem

In nominal control allocation problem, the minimum energy cost of control surface deflections is usually considered as the allocation objective. In addition, various performance indices, such as minimum/maximum drag index and max lift index, may need to be taken into account during certain allocation circumstances. Therefore, a multi-objective optimization problem is formed in each different flight task mode.The multi-objective cost functions associated with the control allocation problem in a specific flight phase generally have the following candidates:

where u is control input vector, subscript p denotes previous,CDand CLdenote nondimensional drag and lift forces,respectively. For each different flight phase, the multi-objective control allocation problem in terms of specific performance indices of aircraft, i.e., Jk(k=1,2,3,4) from Table 1, can be formulated as

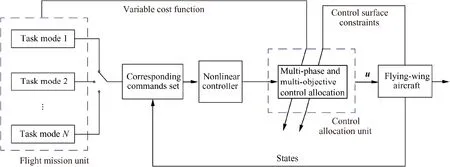
Fig. 2 Structural sketch of a multi-phase control system.

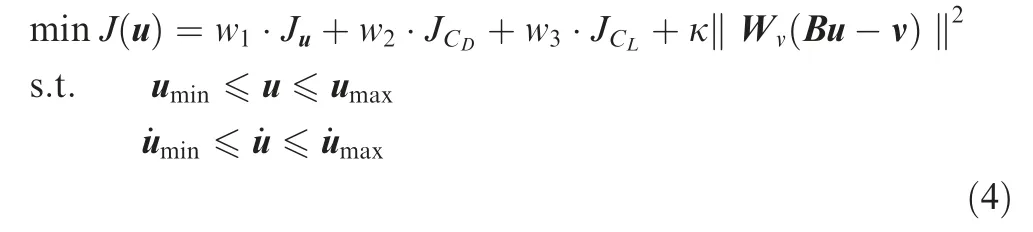
where wi(i=1,2,3) denotes the weight factor for the ith performance index, e.g., minimum deflections, minimum/maximum drag and maximum lift. Wvis a diagonal weighting matrix. κ is the penalty factor. In the remainder of this paper,the method to weigh these optimization objectives for each flight phase and how to obtain a comprehensive index for an overall flight mission according to the features of different flight phases will be investigated and given. To ensure the real-time optimization for the control allocation problem, the active set method is used in this paper.

3. Construct comprehensive index for multi-phase and multiobjective control allocation

For the control allocation in the whole process of a task chain,it is necessary to design a comprehensive optimization index for the multi-objective control allocation problem during the multi-phase flight. In order to realize path tracking control online, this paper combines a trajectory controller with realtime optimization based control allocation. In the trajectory controller, incremental backstepping control law is adopted to design the angular commands tracking controller. In the overall multi-phase control process, the weighting factors for the multi-objective indices are dynamically adjusted according to the control preference for given flight task modes, e.g.,climbing, cruise, maneuver and gliding.

3.1. Index synthesis in the control allocation problem for an overall flight mission

For each different flight phase, it is unreasonable to only consider a single index such as minimum drag or maximum lift,and a comprehensive index constructed from weighted multiple objectives is more suitable to construct the control allocation problem. Once an aircraft flies from one flight phase into another,the comprehensive index should vary according to the control preference and expert experiences.

To synthesize multiple indices and to obtain a reasonable comprehensive index for the control allocation problem, each index should be compared with the others to determine their contributions. For this purpose, the AHP method is used in this paper to determine the varying weighting factors for different indices contained in the comprehensive index.

The AHP method relies on expert knowledge to calculate weights for constructing comprehensive optimization index.Although the AHP has strong subjectivity, its reasoning process based on expert knowledge conforms to the thinking process of human beings, and its implementation is simple. Using the AHP method, the reasoning and deducing logic can be adjusted flexibly according to the actual situation and the actual control preference adjustments.The detailed implementation process of AHP is depicted in Fig. 3.

The procedure of constructing the comprehensive optimization index for the overall control allocation problem is summarized as follows in detail.

Step 1. Construct the hierarchical model for each flight phase according to Fig. 4.

For control allocation of the flying-wing aircraft, the relevant factors for the AHP method include the control surface deflection index, the drag index and the lift index.

Step 2.Construct the pairwise comparison matrix for AHP method.

For each flight phase,the control allocation problem is formulated into a multi-objective optimization problem, where different performance indices shown in Fig. 4 need to be considered in a comprehensive way. For Eq. (4),the weights need to be determined using the AHP method. The key issue in using the AHP method is to construct the judgement matrix according to the control requirements and the expert knowledge on flight principles.

When making the comparisons in the AHP method, two key issues are as follows:(A)which of the two factors in comparison has the greater strength; (B) how much greater it is.The matrix of pairwise comparisons is constructed as follows(see Eq. (5)):

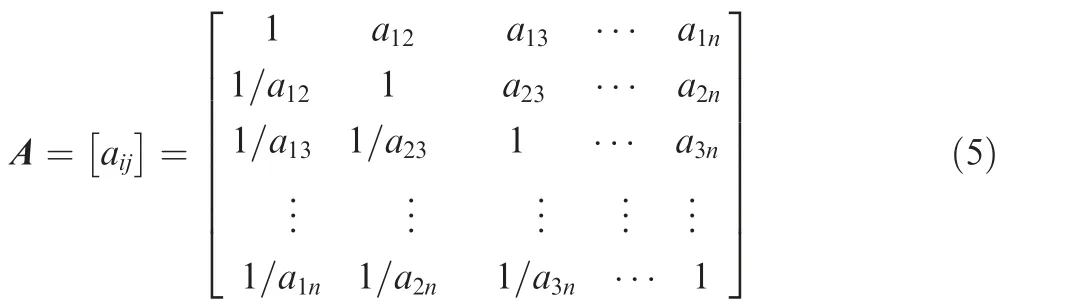
Fig. 3 Flowchart of AHP method in calculating weights for comprehensive indices.

Fig. 4 Hierarchical control allocation model for each flight phase.

where aij=1/aji,and the value of aijmay vary from 1 to 9;1/1 indicates equal importance, while 9/1 indicates extreme importance.

For the climbing phase, Ju, JCD,minand JCLare compared with each other considering the preference of the climbing task.For phase one,compared to the control energy cost specification, the drag force is expected to be small, and the lift is expected to be large.Therefore,a12is selected as 1/2,and a13is selected as 1/9.To summarize,the matrix of pairwise comparisons is chosen as follows based on expert knowledge:

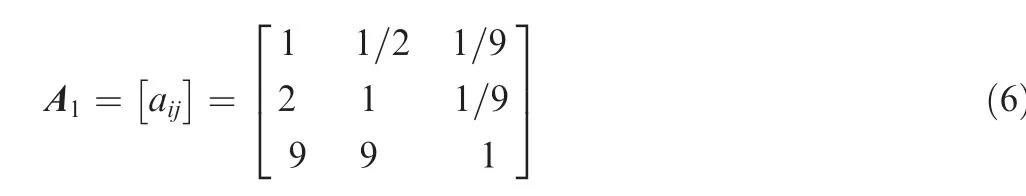
For the cruise phase, Ju, JCD,minand JCLare compared with each other considering the preference of the cruise task. For phase two, compared to the control energy cost specification,the drag force is expected to be small, and the lift is expected to keep constant or to increase upon requirements. Therefore,a12is selected as 2/1, and a13is selected as 5/1. To summarize,the matrix of pairwise comparisons is chosen for the cruise phase as follows based on expert knowledge:

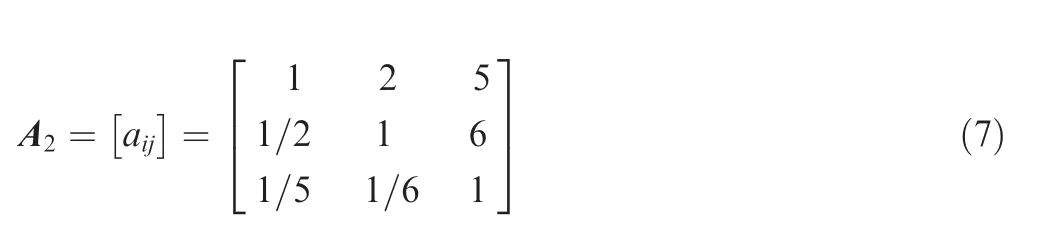
For the maneuver phase, Ju, JCD,minand JCLare compared with each other considering the preference of the maneuver task. For phase three, compared to the control energy cost specification,the drag force is expected to be small,and the lift is expected to keep at a constant level.Therefore,a12is selected as 1/1, and a13is selected as 1/7. To summarize, the matrix of pairwise comparisons is chosen for the maneuver task as follows based on expert knowledge:

For the gliding phase,Ju,JCD,minand JCLare compared with each other considering the preference of the gliding task. For phase four, compared to the control energy cost specification,the drag force is expected to be large,and the lift is expected to keep at a constant level. Therefore, a12is selected as 1/6, and a13is selected as 1/3. To summarize, the matrix of pairwise comparisons is chosen for the gliding/approaching task as follows based on expert knowledge:

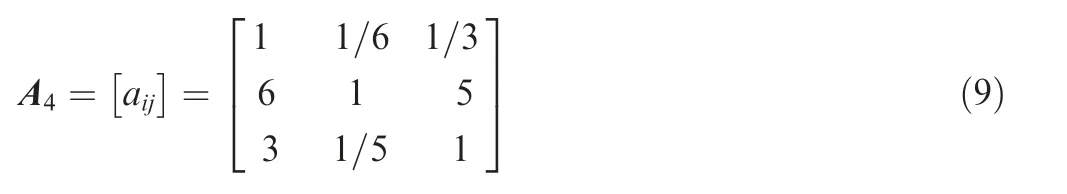
Step 3.Consistency check of pairwise comparison matrix A

Before calculating the final weighting matrix for Eq.(4),the consistency level of matrix A needs to be checked.The detailed procedures for this process are as follows:

(1) Calculate the largest eigenvalue λmaxof matrix A given by Eqs.(6)-(9):

If CR is equal to or less than 0.1,matrix A is considered to be acceptable.Otherwise,the pairwise comparisons have to be repeated to obtain acceptable matrix A.

Note that the matrices of pairwise comparisons given in Eqs.(6)-(9)satisfy the consistency check by Eq.(8),the consistency values take the following values for the matrices A1to A4: CR1=0.0462; CR2=0.0739; CR3=0.0017;CR4=0.0810.

Step 4. for each flight phase, calculate the weights for Eq.(4) based on the judgement matrix, i.e., the pairwise comparison matrix.

Firstly,we need to calculate the eigenvalues of the pairwise comparison matrix A, and then perform the normalization.Finally, the following weighting vector can be obtained for Eq.(4)at each flight phase with respect to minimum deflection,minimum drag, maximum drag and maximum lift requirements:

(1) Calculated weights for multiple optimization indices in different flight phases

For different flight phases as shown in Fig. 2, the weights for different optimization indices (see Eq. (4)) are calculated using the abovementioned method, and are given in Table 2.

(2) Reasonability analysis and remarks

The weight settings for each task as shown in Table 2 are reasonable according to expert knowledge. For example, in the climbing phase, it is necessary to increase lift and reduce drag, so the weights of lift and drag index are larger than the weight of control surface deflection index. In the cruise phase, it is necessary to reduce surface deflection and drag to reduce fuel consumption while the demand for lift is relatively small, so the weights of drag index and control surface deflection index are large relatively.

Remark 1.The determination of matrix A in Eq.(5)reflects the cognition and judgement capability of the designer, and therefore, it is subjective. Limited to the capability of human,if the original decision-making problem has a dimension of n which is higher than 9, this problem should be divided into multi-layer sub-problems to facilitate the determination of elements in matrix A.

3.2. Overall optimization model for multi-phase and multiobjective control allocation problem

Based on previous statements of the multi-phase and multiobjective control allocation problem, the optimization based overall control allocation model can be founded (see Fig. 5).The previously designed task chain will be chosen as an example to explain the modules and the corresponding functions in the remainder of this paper.

As depicted in Fig.5,the control allocation problem is usually addressed by solving a constrained optimization problem.In this paper,four different flight phases are considered,which constitute an overall flight mission, i.e., the designed test benchmark. As discussed earlier in previous section, for each single flight phase, the optimization index is synthesized from control energy cost, drag index and lift index.

For a multi-phase flight, i.e., an overall flight mission, different control preference,which is reflected by the control allocation index Jiwith i=1,2,3,4 denoting the ith flight phase,is pursued in different flight phases. Therefore, the control allocation mode,i.e.,J1,J2,J3or J4,should be adjusted according to the change of the flight phases.For example,when the flight task is at phase one, the aircraft is operated for climbing. In this case, J1should be used as the cost function in the control allocation part. Correspondingly, if the aircraft enters phase two,J2should be used as the cost function in the control allocation part. To summarize, for different flight phases, the weighting factors in Eq. (4) should be adjusted dynamically when the aircraft transfers from one flight phase to another.In this paper, the AHP method given in previous section is used to obtain matched and synthesized control allocation index for different flight phases.

Table 2 Weights for different optimization indices in comprehensive index.

Fig. 5 Optimization model for multi-phase and multi-objective control allocation problem.

3.3. Real-time optimization solver for control allocation

As shown in Eq. (4), the multi-phase and multi-objective control allocation problem can be formulated into a constrained nonlinear optimization problem.In addition,this optimization problem should be solved in a highly efficient and real-time manner to match the computational efficiency of regular flight controllers. According to Ref.26, the Quadratic Programming(QP) allocation method solved with the Active Set Algorithm(ASA) is suitable for solving the nonlinear control allocation problem mentioned above. The QP allocation method with ASA solver has good property in terms of convergence consistency and real-time implementation. In addition, the QP allocation method with ASA has the advantages that it enables flexible adjustment of the cost function due to its rolling optimization mechanism and the conciseness of the quadratic-form optimization index. Consequently, it is suitable to solve the abovementioned multi-objective control allocation problem where the comprehensive allocation index is varying with the changes of the flight phase.

4. Simulation results and analysis

To validate the multi-phase and multi-objective control allocation method proposed in Section 3, the task chain shown in Fig.1 of Section 2.1 is used to perform simulation experiments.In the flight control system of the flying-wing aircraft, the Incremental Backstepping(IBKS)control law is used to design an adaptive nonlinear flight controller, and to generate the demanded control moments in all the three control channels.For the overall flight mission depicted in Fig.1,the flight path command tracking performance is checked to demonstrate the applicability of the proposed multi-phase and multi-objective control allocation method.

4.1. Aircraft model and controller

In this paper, the ICE flying-wing aircraft model was established according to Ref.4. As shown in Eq. (13), the effectiveness of each control effector is highly nonlinear with regard to the changes of angle of attack or sideslip angle. Besides, each control effector is strongly coupled with the other control effectors,and each control effector can yield moment contributions to all three different control channels namely the roll,pitch and yaw axes.

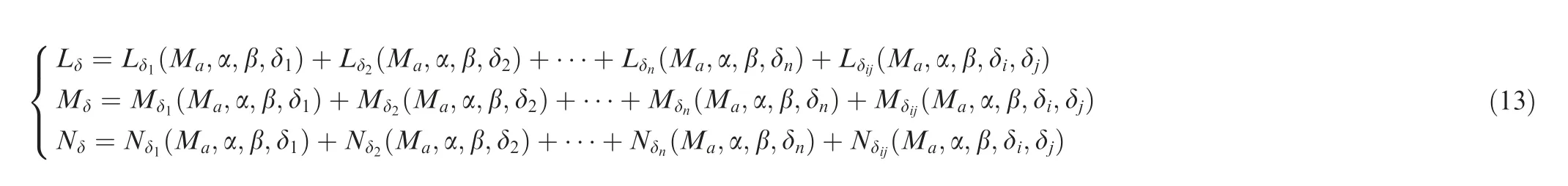
where L,M,N are moments,δ,Ma,α,β represent control input deflection, Mach number, angle of attack and sideslip angle,respectively.Further explanations for the coupling and nonlinear characteristics of the control effectors are given in Fig. 6 with Cl, Cm, Cnthe nondimensional moments. When the deflection position of the All-Moving wing Tips (AMT) or the Elevon changes, the control effectiveness of these effectors varies a lot.For different angles of attack,both AMT and Elevon have different control effectiveness. Furthermore, if the deflection position of AMT or Elevon changes, either of them will yield control moments in all three different channels. In this paper, the control effectors are ranked according to their efficiency, and the top seven control effectors are viewed as the most representing effectors.In the simulation experiments,only the following seven control effectors are used for convenience of the results analysis:Left AMT(LAMT),Left Elevon(LELE),Pitch Flap(PF),Right AMT(RAMT),Right Elevon(RELE), Pitch Thrust Vectoring (PTV) and Yawing Thrust Vectoring (YTV).

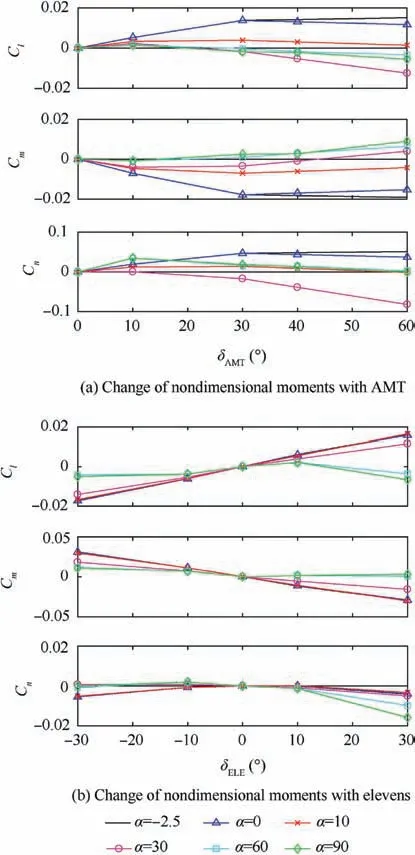
Fig. 6 Contribution of effectors to moments.

For double-loop angular controller design,the equations of motion of the ICE flying-wing aircraft have the following expressions:

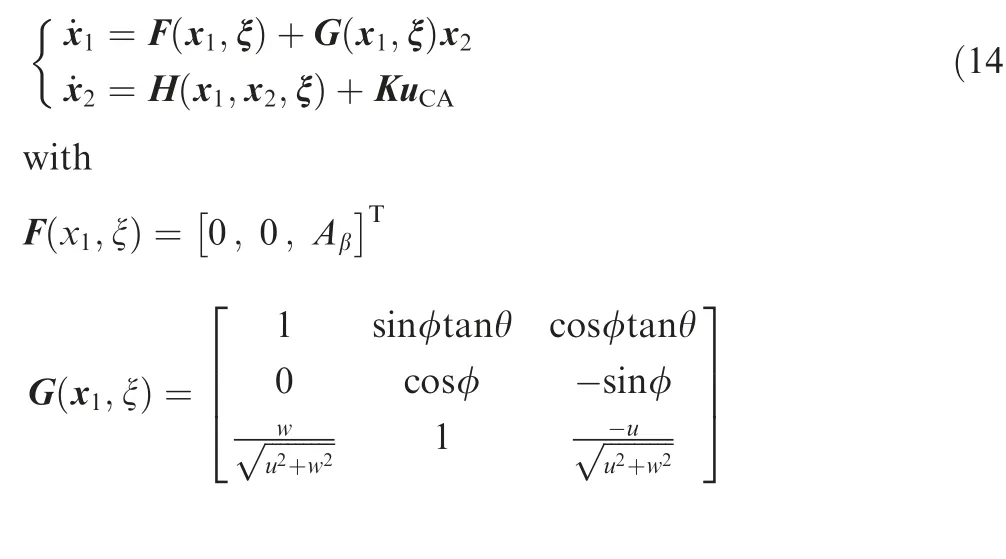
With c1, c2the controller gains to be determined. α1is the virtual control input vector for x2= p,q,r[ ]T.

The control diagram of the overall flight control system,including the flight path controller and the control allocation unit, is shown in Fig. 7.

4.2. Reference command generation from flight task

Before the simulation of the designed task chain shown in Fig. 1 can be performed, we still need to firstly generate executable reference commands for the control system shown in Fig.7.That is,the flight task requirement for each stage shown in Fig.1 needs to be converted to specific reference commands that the flight path controller shown in Fig.7 can directly refer to.In each control and allocation mode,the original reference commands that the controllers can receive are the Flight Path Angle (FPA), and therefore, the reference commands of the normal load factor, which are associated with the flight task mode, need to be converted into the FPA commands.

For the climbing mission at phase one,the flight path angle γ is regulated to 3 deg quickly, and then it is kept constant to accomplish the climbing task. For the cruise mission at phase two,the climbing task is stopped,and the reference commands for the flight path angle γ is chosen as zero.In the gliding mission at phase four,the flight path angle is regulated to-3 deg rapidly and then keeps constant.

For the maneuver mission at phase three, the normal load factor is chosen as the controlled variable to reveal the maneuverability of the closed-loop control and allocation system.For the maneuver flight phase, how to convert the commands for normal load factor nzinto the commands for the flight path angle is derived as follows. According to the basic knowledge from flight dynamics, the following equations hold for the motions of aircraft:

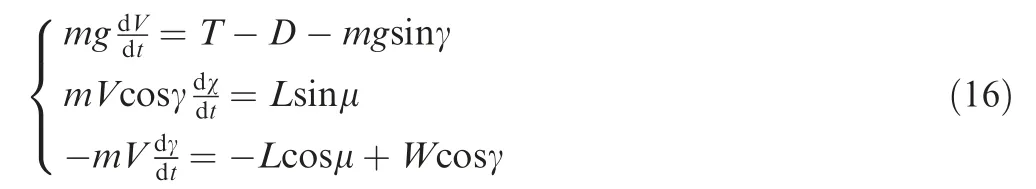
with T,D,L,W,χ,μ,m,g,V the thrust of the engine,the drag,the lift, the weight, the heading angle, the bank angle, mass,gravitational acceleration, and airspeed of the aircraft, respectively. Eq. (16) can then be rewritten into the following expression:

with nx,ny,nzthe load factors along the body X,Y and Z axes.If χ=0 is assumed for the investigation of only the longitudinal motions of aircraft, we get the following concise formulation:

Finally, Eq. (18) is used to generate the commands for γ from the load factor commands. Correspondingly, the block diagram for the implementation of Eq. (18) is given in Fig. 8.

The designed command for the normal load factor is shown in Fig. 9(a) for the maneuver flight phase, and then the flight path angle command is calculated correspondingly for this maneuver mission.Finally,the flight path angle command corresponding to the overall task chain is obtained,and is plotted in Fig. 9(b).

4.3. Results and analysis

To validate the multi-phase and multi-objective control alloca-

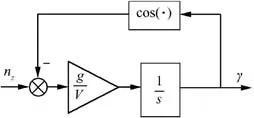
Fig. 8 Block diagram of command converter from load factors.

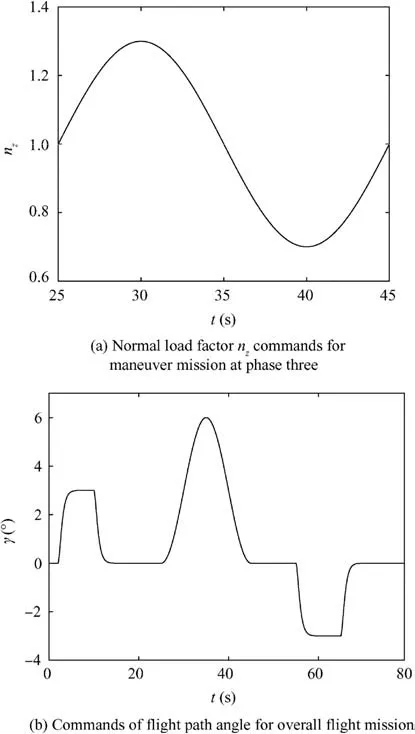
Fig. 9 Commands conversion from nz to flight path angle.

tion method, the research results are given and analyzed. In this paper, the results mainly include two parts: the weights for the comprehensive optimization indices determined using the AHP method, and the command tracking simulation results obtained using the flight path controller and the control allocation module embedded in the controller.

In this paper, the simulation results are mainly analyzed from the following aspects: task completion satisfaction, control allocation precision and computational efficiency, and moment tracking performance of the control surfaces.

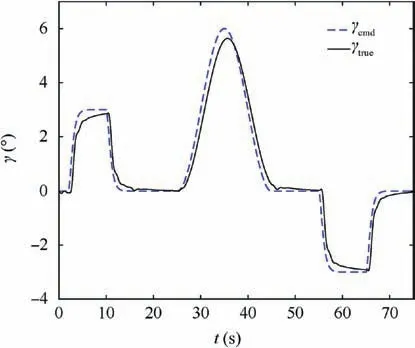
Fig. 10 Tracking of flight path angle.

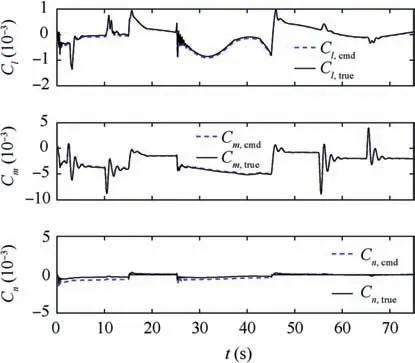
Fig. 11 Control allocation results of moments.

Fig. 12 Results of controlled variables.

Firstly, the task completion satisfaction level of the overall flight control system is analyzed by checking the command tracking performance of the flight path angle γ,and the results are plotted in Fig.10.The results showed that the flight control system equipped with the multi-phase and multi-objective control allocation module can track the pre-designed flight path well with very small tracking errors,that is to say the proposed control allocation method has the capability to accomplish the designed task chain as shown in Fig. 1 with high level of performance.

The multi-phase and multi-objective control allocation part is also validated independently in this paper, and the results are given in Fig. 11. It can be seen that the multi-phase and multi-objective control allocation method designed in this paper can track the commands of the demanded moments well,which ensures high-level allocation accuracy and satisfactory tracking accuracy for the overall flight controller.

In addition to the analysis of task completion satisfaction level, validation for each loop of the controller, i.e., the angular loop and the angular rate loop,is also performed.The simulation results are shown in Fig. 12. It can be seen that the commands and real states for roll angle and pitch angle almost coincide, and the tracking error is small. The tracking of sideslip angle is not ideal,but the tracking error is small relative to roll angle and pitch angle, which has little impact on mission completion. This is due to the lack of traditional vertical tail in the flying-wing aircraft, which makes the control ability of the flying-wing aircraft insufficient in the directional direction.Note that the task chain is designed in the longitudinal plane in this paper.Therefore,in the simulation,the main task is to validate the control system in the longitudinal direction, and the validation of the controller in the lateral-directional direction is not paid efforts in this paper.As shown in Fig.12,the tracking errors for the lateral-directional controlled variables are also within the allowable error range. The tracking errors of the angular rate loop are also small, and some fluctuations appear only when the task mode (phase) is switched.

The use of the control surfaces also needs to be examined and analyzed. The deflections of the aerodynamic control surfaces and the pitch and yaw thrust vectoring are shown in Fig.13(a).Because the position and rate constraints are taken into account in the control allocation, it is also necessary to verify whether the actual use of the control surfaces meets the constraints. The changing rates of the control surfaces are shown in Fig. 13(b).

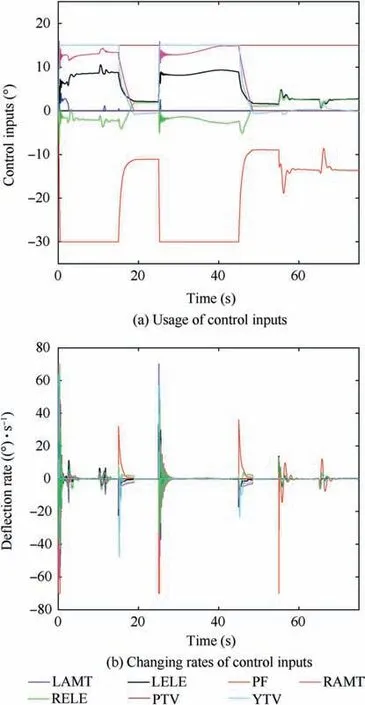
Fig. 13 Results of controlled inputs.

It can be seen from Fig.13 that the flying-wing aircraft have different demands for the control surfaces under different tasks, this is due to the changes of the comprehensive indices used in the control allocation problem. For example, the demand for lift in cruise is less than that in other tasks, so the corresponding use of the control surfaces are relatively less.The demand for lift in the climbing or the maneuver stage is relatively large, so the control surfaces with higher lift efficiency are used more to increase the lift. The requirement of drag in the gliding stage is larger than that in the cruise stage,so the use of the control surfaces,i.e.,the left and right elevons and the pitch flap, in the gliding phase is relatively more than that in the cruise phase (see Fig. 13).

Finally,according to the use of the control surfaces and the deflection rates, it can be seen from Fig. 13 that the use of the control surfaces can well meet the position and rate constraints.

Remark 2. Using the proposed control allocation method,the flight control system is allowed to pursue preferable performance in terms of J1, J2, J3or J4. Due to the use of an incremental control allocation framework and method, smooth control of the controlled variables is guaranteed during the transition of the multi-objective optimization index Jk.

5. Conclusions

In this paper,a multi-phase and multi-objective control allocation problem of flying-wing aircraft is studied. On the basis of control allocation problem description, the comprehensive index synthesizing method,which is based on the analytic hierarchy process method, is proposed for multi-phase flight.And then the method is validated together with the nonlinear controller using the designed task chain. For the designed task chain with five different phases,the path tracking performance are analyzed. Specifically, the results for flight path angle tracking, control allocation, loop tracking and the use of control surfaces are given. The results showed that the proposed multi-phase and multi-objective control allocation method based on real-time optimization can accomplish the task of control allocation with the preference for each flight phase being actively taken into account. In the future, lateral flight path maneuvers should be studied to further validate the applicability of the proposed method.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (No.11502008), Aeronautical Science Foundation of China (Nos. 2017ZA51002, 20185702003) and the Fundamental Research Funds for the Central Universities of China (No. YWF-19-BJ-J-280).