“平面直角坐标系”学习指导

王宗信

学习平面直角坐标系的相关知识，可以帮助我们建立图形与数量间的联系，并为几何问题和代数问题的相互转化打下基础.

一、认识有序实数对

人们在乘坐列车或飞机出行时需要购买车票或机票，车票或机票上标明了乘客的具体座位.到电影院看电影需购买进场票，票上明确标出座位在第几行第几列（几排几号）.同样，教室里的座位也是用这种方法来描述的，同时我们也知道，在同一个电影院里.3排4号与4排3号不是同一个位置，所以可以用一对有序实数对表示位置，3排4号用有序实数对（3，4）表示，4排3号用有序实数对（4，3）表示，利用有序实数对，可以准确地表示一个位置.

气象部门用经纬度来描述台风中心的位置变化，这也是用数量来描述位置变化的.数量与位置之间有着紧密的联系.

二、平面直角坐标系

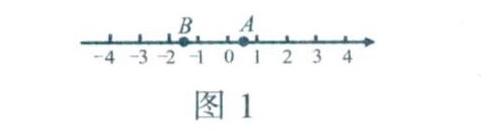
用一对数确定一点位置的做法，在日常生活中很常见.在上一章里，我们知道数轴上的点与实数是一一对应的，数轴上每个点都对应着一个实数，这个实数叫作这个点在数轴上的坐标.例如，图l中，点A在数轴上的坐标是0.6，点B在数轴上的坐标是-1.5.

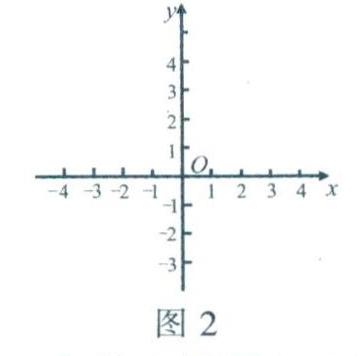
如图2.我们可以在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系.水平的叫戈轴或横轴，取向右为正方向;竖直的叫y轴或纵轴，取向上为正方向.x轴与y轴的交点叫平面直角坐标系的原点.两条坐标轴的原点必须重合，单位长度可以相同，也可以不相同.

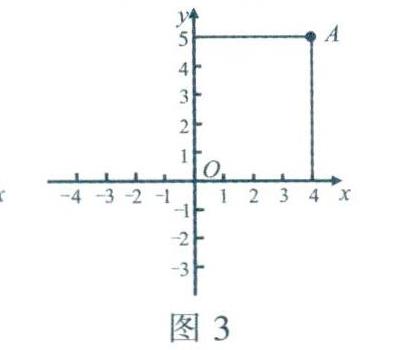
有了平面直角坐标系，平面内的点就可以用一个有序实数对来表示了，例如，在图3中，由点A分别向x轴和y轴作垂线段，垂足在x轴上的坐标是4，我们把这个数叫作点A的横坐标;垂足在y轴上的坐标是5，我们把这个数叫作点A的纵坐标.也就是说点A的横坐标是4，纵坐标是5，有序实数对（4，5）就叫作点A的坐标，注意横坐标要写在前，纵坐标要写在后，顺序不可乱.

点的坐标用（a，b）来表示，a表示这个点的横坐标，b表示这个点的纵坐标，在括号内横坐标写在前，纵坐标写在后，中间用“，”隔开，顺序不可随意更换.用同样的方法可以确定下页图4中点B的坐标是（-2，3），点C的坐標是（-4，一1），点D的坐标是（2.5，-2）.同学们可以发现点E在y轴上，如何确定它的坐标呢？方法是不变的，过点E作x轴的垂线，垂足在x轴上的坐标是O，过点E作y轴的垂线，垂足在y轴上的坐标是-4，所以点E的坐标是（0，-4）.通过作图找点E的坐标，可以发现y轴上所有点的横坐标都是0.请同学们思考：x轴上点的纵坐标是多少呢？请在x轴上任取若干点确定它们的坐标，你会有所发现的！

反过来，如果知道一个点的坐标，那么我们可以通过作图找到这个点，比如已知一个点的坐标是（4，3），我们这样来找这个点：在x轴上找到坐标为4的点，过这个点作x轴的垂线，再在y轴上找到坐标为3的点，过这个点作y轴的垂线，两条垂线的交点就是我们需要寻找的点（4，3），即图4中的点F.

建立平面直角坐标系后，这个平面称为坐标平面，整个坐标平面被两条坐标轴分成I、Ⅱ、Ⅲ、Ⅳ四个部分（如图5），每个部分称为象限，x轴正半轴与y轴正半轴所夹部分称为第一象限，x轴负半轴与，轴正半轴所夹部分称为第二象限，x轴负半轴与y轴负半轴所夹部分称为第三象限，x轴正半轴与y轴负半轴所夹部分称为第四象限.同学们可以结合图4中B，C，D，F四个点的坐标来发现四个象限内点的坐标的符号，完成表1的填空.

三、利用平面直角坐标系解决简单的问题

例1如图6，正方形ABCD的边长为6，如果以点A为坐标原点，线段AB所在直线为x轴，建立平面直角坐标系，那么y轴是哪条线？写出正方形的顶点A，B，C，D的坐标.

分析：以点A为坐标原点，线段AB所在直线为石轴”：双向延长线段AB得到直线AB，以点A为原点，以向右的方向为正方向，直线AB为x轴，因为正方形中LDA B=900，所以AD⊥AB，根据平面直角坐标系的定义，可以建立平面直角坐标系，如图7.

解：建立平面直角坐标系，如图7，直线AD为y轴.

点A，B，C，D的坐标分别是（0，0），（6，0），（6，6），（0，6）.

请同学们思考：直线BC上点的坐标有什么共同之处？直线CD上点的坐标有什么共同之处？你能得到哪些结论？

请同学们以正方形的对角线交点为原点，边AD，BC的中点所在直线为x轴，边AB，CD的中点所在直线为y轴，建立平面直角坐标系，并写出正方形的顶点A，B，C，D的坐标，你会有哪些发现？

练一练

如图8，四边形ABCD是平行四边形.

（1）写出平行四边形ABCD各个顶点的坐标.

（2）把平行四边形ABCD向右平移3个单位长度得到平行四边形A'B'C'D '，请画出平行四边形ABC'D，并写出它的四个顶点的坐标，

参考答案：（1）点A（-3，3），B（-5，-2），C（4，-2），D（6，3）. （2）略.