大跨度斜拉桥钢混叠合加劲梁制造线形研究

刘斌

(长沙理工大学 土木工程学院，湖南 长沙 410114)

对于悬臂拼装施工的叠合梁斜拉桥，由于钢主梁在钢结构制造厂家事先预制完成，现场悬拼时节段之间的转角不可随意调整，只能进行切向安装，制造预拱度计算对悬拼钢梁至关重要。制造预拱度是给钢结构厂家下达的线形加工指令，即钢梁的无应力制造线形，若钢梁的制造预拱度有误差，将导致钢梁斜拉桥梁段安装时前后梁段间转角与制造线形不一致，影响结构受力，甚至影响全桥的运营。以往较多采用零初始位移法(将新生成节点的初始位移指定为零，以该点为零点记录节点的累计位移值)计算预拱度，该方法的计算结果是安装线形，无法直接得到制造线形，基于零初始位移法的计算模型需结合各节点竖向位移和转角位移才能计算出制造预拱度。切线位移法是将新节点初始位移指定到沿着已成梁段悬臂端切线上，把到节点偏移零位置的距离作为累计位移值，其计算结果为制造预拱度，且计算中不存在预拱度之间的转化。

1 制造预拱度的计算原理

在现场施工过程中，钢梁是按照前一个桥梁节段的切线方向用高强度螺栓拼装，这种独特的施工方式会带来不可忽视的假想位移(也称虚位移)，故结构的实际位移(也称为总位移)由结构荷载产生的纯位移和虚位移组成。计算钢梁的制造预拱度是为了向钢梁制造厂家下达制造线形指令，钢梁制造完成后在厂内预拼装，达到构件精度和线形要求后将钢梁运输到现场，在现场按钢主梁的切线方向进行拼装，使成桥后实际桥梁线形与成桥理论线形基本一致。制造预拱度等于施工过程中各施工阶段总位移的反方向的值。

以3个节段的悬臂拼装梁施工为例，为了形象直观，令梁段在变形后仍为直线节段。如图1所示，在悬臂拼装完第1个梁段后，节点1处产生的位移为δ11，节点2和节点3处分别产生假想位移δ21、δ31；在悬臂拼装完第2个梁段后，节点1和节点2处产生的位移分别为δ12、δ22，节点3处产生假想位移δ32，这3个位移全都不包含悬臂拼装梁段1时的假想位移；在悬臂拼装完第3个梁段后，节点1和节点2处产生的位移分别为δ13、δ23，节点3处产生的位移为δ33，这3个位移全都不包含悬臂拼装梁段1和梁段2的位移。

图1 悬臂拼装各梁段时的位移

悬臂拼装完第3个梁段后各点的总位移为：

节点1的总位移=δ11+δ12+δ13

节点2的总位移=δ21+δ22+δ23

节点3的总位移=δ31+δ32+δ33

各节点的纯位移为：

节点1的纯位移=δ11+δ12+δ13

节点2的纯位移=δ22+δ23

节点3的纯位移=δ33

如图2所示，制造预拱度是一条连续线形，中间没有出现突变，如果严格按施工预拱度进行施工，拼装钢主梁时只需按照制造预拱度与前一个桥梁节段连接，再利用斜拉索对钢主梁线形进行微调，即可使实际成桥线形与理论成桥线形基本一致。

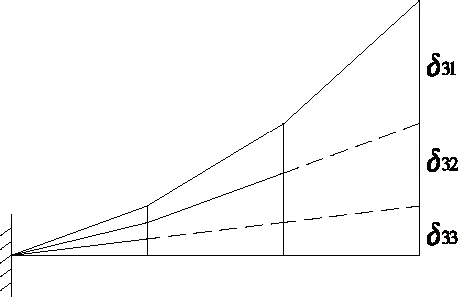
图2 制造预拱度曲线

2 制造线形实例研究

某叠合梁斜拉桥全长866 m，为双向坡双塔双索面混合式叠合梁斜拉桥(主跨480 m)，设计速度80 km/h。索塔为江鱼拱形砼桥塔，总高182.922 m，桥面以上索塔高度为128.6 m。承台顶面至塔冠顶面采用承台+群桩基础。为减小索塔拉应力，塔柱设置井字形水平预应力钢束，局部范围内设置竖向预应力钢束。中跨采用钢箱叠合梁，边跨采用预应力砼梁，钢混结合段位于中跨索塔附近。下面以该桥为例，研究悬臂拼装钢梁的制造线形。

2.1 模型建立

采用MIDAS/Civil软件进行建模计算。边界条件如下：主塔桩基础由土弹簧约束，桥墩底部固结；梁端及辅助墩处竖向约束，纵向不约束；主梁与主塔竖向、横向约束。计算模型见图3。

图3 MIDAS计算模型

2.2 软件计算特点

利用MIDAS软件计算钢梁制造预拱度时，在施工阶段分析控制数据对话框中选择构件沿初始切线位移方向激活选项并选择需激活该选项的结构组，施工新的桥梁节段时，新节段按照上一个桥梁节段的切线方向安装，在后处理模式分析时，可在分析结果中分别提取钢梁的切线位移和预拱度。其中钢梁的切线位移包含结构受力、至竣工阶段的收缩徐变、切线拼装引起的位移总和，预拱度考虑的是成桥10年后收缩徐变和0.5倍活载引起的位移。

2.3 制造线形计算结果与分析

该桥制造线形计算结果见表1、图4。

表1 某叠合梁斜拉桥制造线形计算结果

图4 钢梁制造线形

由图4可知：钢梁的制造线形为一条连续光滑的曲线。但在实际制造过程中，将梁段制造为光滑曲线既费时费力，又无实际工程意义，多采用以直代曲的方式制造。制造过程中误差是不可避免的，故悬臂拼装施工时应以安装线形来定位梁段标高，以更好地进行线形控制，确保最终达到设计线形。

3 结语

该文根据现有叠合梁斜拉桥制造线形计算理论，采取适用于叠合梁的切线位移法计算钢梁的制造预拱度，并以某叠合梁斜拉桥为例，依据该桥结构特点和参数建立桥梁空间有限元计算模型，通过对整个施工过程的模拟，获得其悬臂拼装钢梁的制造线形，为该桥提供合理的线形数据。