浸水条件下路基当量回弹模量分析

祁孔庆, 汤钧尧，黄晓明

(东南大学 交通学院，江苏 南京 211189)

近年来，我国在海外地区的公路建设业务发展迅猛.在非洲、东南亚等热带地区，雨量充沛且集中，引发路基结构季节性浸水，湿度的改变对路基回弹模量产生明显影响，土体刚度明显降低，路面荷载下的结构响应随之增大，对路面结构的长期性能造成不利影响[1].影响路基湿度场的因素众多，地下水位的抬升、降雨、地表水分的渗入和蒸发等作用都会引起湿度的改变[2].柳志军等[3-4]建立了不同初始湿度和降雨强度下的路基模型，分析了路基湿度场的变化规律.为了定量预估湿度对路基回弹模量的影响，LIANG R.Y.等[5]提出考虑非饱和土中基质吸力影响的回弹模量本构模型，但目前该类本构模型在有限元分析中的应用较少.由于路基回弹模量具有明显的应力依赖性，且受湿度、材料性质等各种因素影响，各位置回弹模量值各不相同.罗志刚[6]提出了结构层模量的计算方法，通过ABAQUS有限元分析和基于弯沉盆面积等效的迭代反算，得到了不同典型路面结构中路基当量回弹模量，以表征路基的整体刚度.由于此方法较繁琐，关于当量回弹模量的简洁计算方法是值得探讨的问题.

为此，通过有限元软件ABAQUS模拟某一特定水位时路基内部湿度场，并选取合适的本构模型反映湿度场对路基材料力学性能的影响，在此模型基础上，分析路面响应，确定路基结构层的等效模量.同样的方法可以得到其他水位对应的路面响应和路基当量回弹模量，最终结果可以为路基设计和水害防治提供参照.

1 浸水路基模型的建立

1.1 路基路面结构及材料属性

以非洲、东南亚等地区在建公路为例，结合当地公路建设及水文地质资料，本研究选取的典型路面结构如图1所示.模型顶面宽度(路面宽度)为16.0 m，底面宽度为46.9 m.路面结构为4 cm AC13 + 6 cm AC20 + 20 cm 级配碎石的3层结构.路基高度为6.0 m，路面和路基按1 ∶1.5放坡，地基深度取12.0 m.初始水位位于地下6 m，取地表高度为y坐标零点，横向中点为x坐标零点.

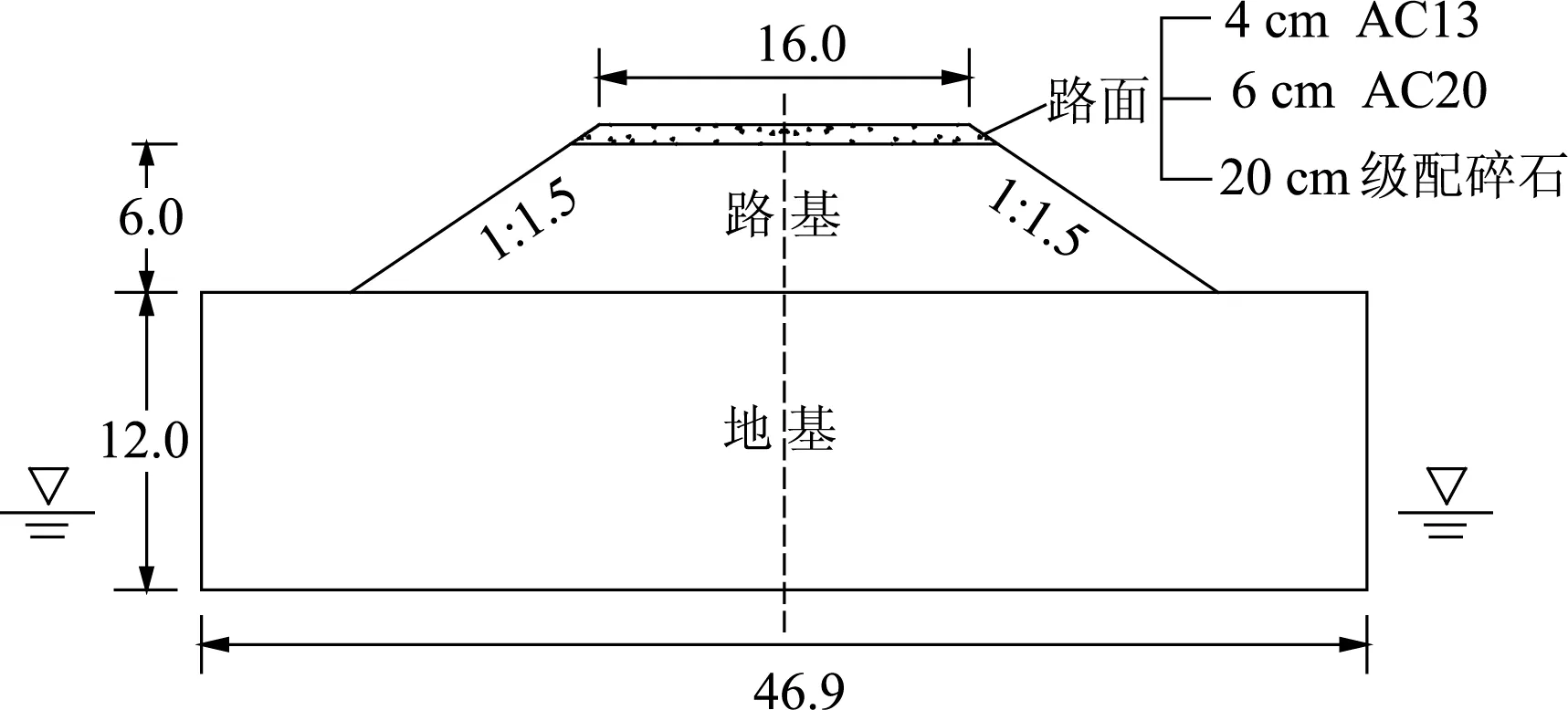
图1 路面结构模型(单位：m)

参考文献[7]确定的路面材料属性如表1所示.目前沥青路面结构设计体系主要以多层弹性体系为基础，其中各结构层的模量、泊松比及结构层厚度是计算路面力学响应的基本参数.为模拟实际工程现场的路面材料结构性能，采用的弹性模量E均为动态模量参数.

表1 路面材料属性

路堤填土与地基采用同种材料，土体的具体参数如下：弹性模量为35 MPa，泊松比为0.3，黏聚力c=15 kPa，摩擦角φ=30°.材料渗透系数Kw同基质吸力ψ的关系如下所示[7]：

ψ=ua-uw,

(1)

(2)

式中：Kws为土体饱和时渗透系数，取5×10-7m·s-1；ua和uw分别为土体中的气压力和水压力，由于土体与大气接触，取ua=0；aw，bw和cw均为材料参数，分别取1 000，0.01和1.7.

饱和度Sr与基质吸力的关系采用FX模型[8-9]，计算如下：

Sr=θw(1+e-1),

(3)

(4)

(5)

式中：θw为体积含水率；C(ψ)为修正函数；θs为饱和体积含水率；ψr为残余含水量对应的基质吸力，kPa；e为孔隙比，其初始值为1.0；a，n，m为拟合曲线参数，分别取值为2 813，0.483 6和3.710 6.

1.2 路基初始状态的确立

根据1.1节中给定的路面结构尺寸创建计算模型，并定义各结构层材料参数.对于路基，除上述参数外，由于非饱和区的存在，还需定义渗透系数随饱和度变化的关系曲线，曲线中的数据由式(1)-(5)计算可得.图 2为渗透系数与饱和度的关系曲线.同时，对于非饱和土渗流问题，必须定义其土水特征曲线，如图3所示.

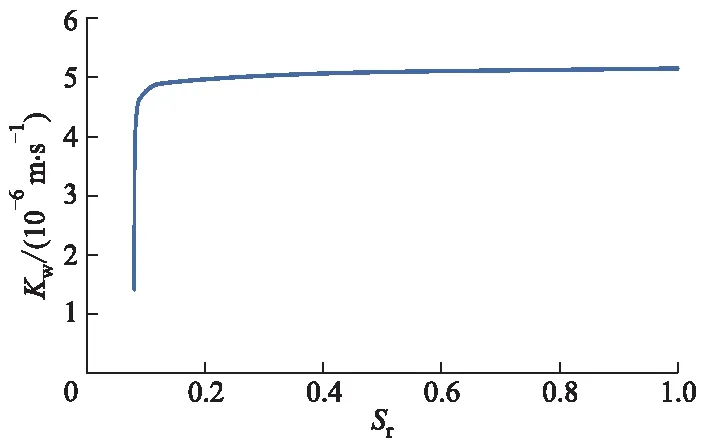
图2 渗透系数与饱和度的关系曲线

图3 土水特征曲线

荷载只考虑结构自身重力，边界条件主要分为位移边界条件与孔隙水压力边界条件.位移边界条件包括模型底部边界控制水平位移和竖直位移以及两侧边界控制水平位移.由于两侧水位的存在，同时需设置孔隙水压力相关的边界条件，即在左、右两侧水位以下部分添加孔隙水压力分布，此时存在如下关系式：

uw=γwh=-10(6+y)，

(6)

式中：uw表示孔隙水压力，kPa；γw为水的重度，取10 kN·m-3；h为水位差，m；y为路面结构模型坐标系中的纵坐标，m.对其他边界不作设置，即默认为不透水边界.

流固耦合分析与平面应变问题当中采用的单元有所不同.流固耦合单元与孔隙水压力相关，故选择单元属性为能够实现孔隙流体应力分析的平面孔隙水压力单元.本例中浸水部分(即地基与路基)采用CPE8P(8节点平面孔隙水压力单元).对于路面部分，采用平面应变分析的CPE8(8节点平面应变单元)即可.为提高后续路面响应结果的精度，划分的网格除全局布种外，需在局部予以细化.对中间部分的网格采取由外向内逐渐加密的处理方式，对面层与基层部分网格纵向加密，划分结果如图4所示.分析得到的初始状态竖向有效应力分布如图5所示，与水平地基成层分布的情况不同.由于边坡的存在，路面、路基及边坡范围内的地基总应力和孔隙水压力同步增加，根据有效应力的定义，竖向有效应力呈现从边坡表面向内逐渐增加的趋势.

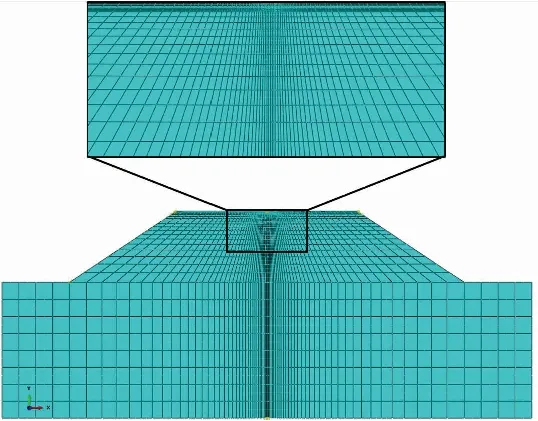
图4 网格划分和顶部细节图

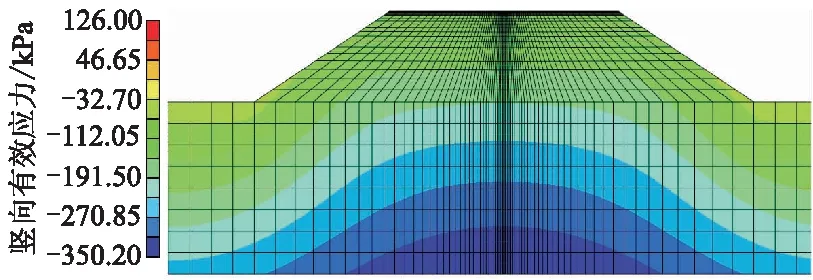
图5 初始状态竖向有效应力分布云图

1.3 水位变化的模拟

将得到的初始状态应力场导入，完成地应力平衡，达到土体内有应力、无位移的状态，即可开始水位变化的模拟与分析.本例中以水位抬升至地上2 m时为例.

由于水位抬升至2 m时，应设置新的孔隙水压力边界条件，以替代原有的关于孔隙压力的边界条件，即

uw=γwh=10(2-y).

(7)

最终分析结果如图6所示.与图5相比可以发现，随着水位的抬升，直至达到稳定，结构各部分的竖向有效应力均大幅降低，这与理论分析的结果是一致的.

图6 浸水水位2 m时的竖向有效应力分布云图

由于ABAQUS中没有提供路基土的回弹模量本构模型，因此需要借助UMAT子程序完成路基各点材料模量的计算，并从场输出中查看模量在不同增量步时的分布[10].本研究采用的路基回弹模量本构模型如式(8)[11-12]所示：

(8)

式中：Mr为回弹模量，kPa；θ为体应力，kPa；τoct为八面体剪应力，kPa；pa为大气压力，通常取为100 kPa；k1，k2和k3为材料参数，分别取值为1 480.32，1.05和-2.982.

UMAT子程序通过与ABAQUS的接口，读取主程序的应力状态，依据本构模型计算路基各点的回弹模量Mr，并根据回弹模量更新各点的应力状态.最终得到水位为地面以上2 m时模量空间分布，结果如图7所示.当水位变化时，将形成不同的孔隙水压力分布，导致路基内有效应力不同，由此计算得到体应力结果差异，将导致模量的差异.

图7 浸水水位为2 m 时路基回弹模量的分布云图

1.4 路面响应分析

为反映路基受浸水条件的影响，采用面层层底拉应变εr和路基顶面压应变εz分别控制面层疲劳损伤和土基的永久变形[13-15].二者均与路基模量具有良好的关联性，故本节通过荷载为峰值时荷载中心εr和εz的计算，分析不同水位条件对荷载作用下路面响应的影响.

为更好地反映路面荷载的实际状况，采用FWD荷载，其时程曲线如图8a所示[13].为了方便计算，通常将其简化为荷载峰值为0.714 MPa，作用时间30 ms，加载半径为0.15 m的半周期正弦函数圆形均布荷载，故实际采用的FWD荷载时程曲线如图8b所示.表 2为FWD荷载半周期变化情况.

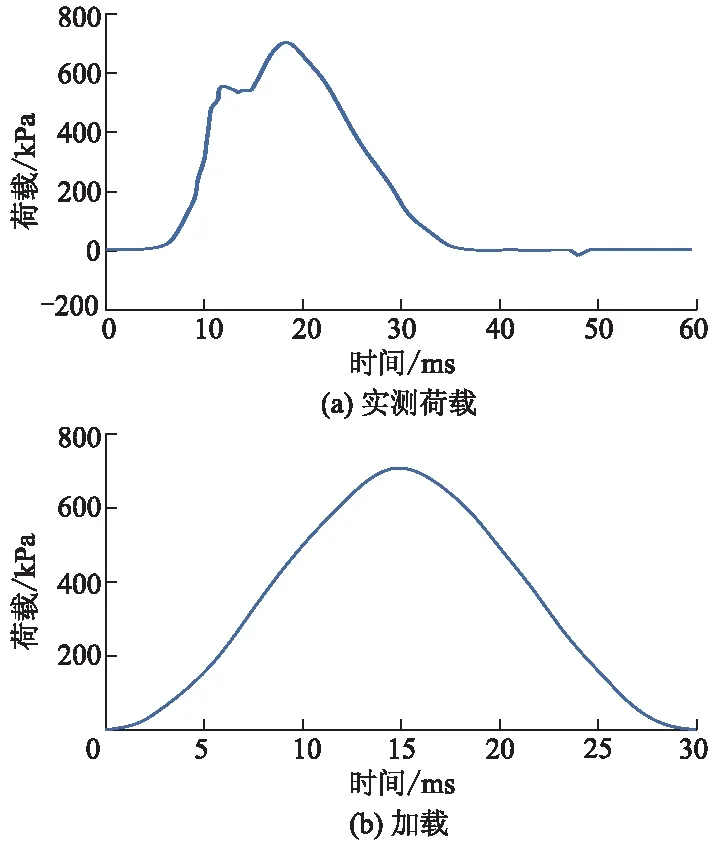
图8 FWD荷载时程曲线

表2 半周期内各时间点上的FWD荷载值 kPa

本例中建立的路面结构为二维平面模型，故需将圆形均布荷载换算为线荷载，根据静力等效原则，换算后的线荷载峰值为

(9)

式中：σ1，σ为线荷载、圆形荷载峰值，kPa；A1为线荷载作用面积，m2;A为圆形荷载作用面积，m2.

同样方法，可以计算曲线其他点的荷载值.荷载为峰值时路基顶面响应结果如图9所示.

造成慢性病患儿与父母之间消极关系的主要有三方面原因：一是患儿父母比健康儿童的父母面临更多的育儿责任和压力，影响了其育儿能力，有些父母甚至会因为在应对孩子疾病时感到无能为力而退出对孩子的照护[24]；二是慢性病患儿比健康儿童更易产生心理和行为问题，让父母感到难以应对，一些父母甚至会因孩子没有达到自己的期望而感到失望和愤怒[16]；三是疾病本身的一些因素会影响亲子沟通，例如听力障碍、未修补的唇腭裂等疾病会损害患儿的语言能力，癌症等疾病需要长期住院治疗，这些因素会阻碍父母与患儿的沟通交流[16]。

图9 FWD荷载为峰值时最大压应变云图

需要注意的是，由于此时路面响应是之前所有分析步积累的结果，若想得到仅由FWD荷载造成的路面响应，需要创建新的场输出量，即由FWD荷载导致的应变值，其值大小为FWD荷载作用0.015 s时的应变值减去FWD荷载施加前的初始应变值.

1.5 路基当量回弹模量计算

为求得整个路基结构层当量回弹模量，采用了基于等效原则的迭代反算算法和基于压应变分布的加权计算方法.

1.5.1基于等效原则的迭代反算

以通过面层层底拉应变εr的迭代反算为例，计算流程如图10所示.

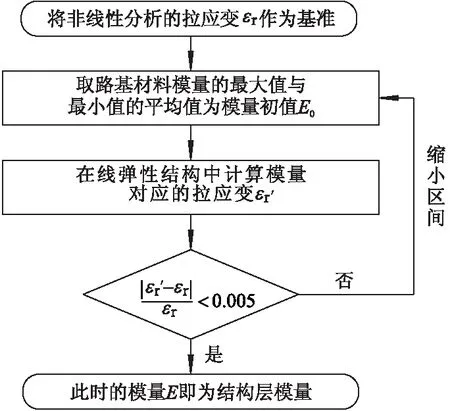
图10 路基当量回弹模量迭代反算过程

迭代反算算法的核心为输入目标值、正演分析计算以及收敛优化算法.借助该思想，笔者在ABAQUS中借助Python语言开发迭代计算脚本，实现等效模量的迭代反算确定方法.步骤如下：

1)目标值读取.目标值由UMAT非线弹性材料模型计算所得，目标值的读取可通过人工读取或脚本读取两种方式，由于读取工作简单，处理方便，不再赘述.

2)正演计算模型.确定路基等效模量的最终目的是给路面设计提供参考，因而正演计算模型的基本框架应该与JTG D50—2017《公路沥青路面设计规范》中的模型一致.即使用与前述非线弹性模型相同的网格形态与边界条件，将土基材料改为线弹性模型，删除孔隙水压力边界条件，只考虑峰值荷载作用下的路面结构静力响应.

1.5.2基于压应变分布的加权计算

在利用UMAT子程序进行结果计算的同时，虽然路基回弹模量是一个中间变量，却也可以将其输出到结果文件中，此时可以得到路基回弹模量的空间分布形态.据此，如果使用合适的权函数对这些模量值进行加权平均，可以直接得到路基整体的当量回弹模量.

问题的关键是权函数的选取.从直观上来说，由于荷载的传递作用，距离荷载越近的土体，所承受的路面荷载应该也越大，即越靠近荷载作用中心的土体，其刚度贡献越大.基于以上判断，权函数的构造应该符合上述规律，即越靠近荷载作用中心的土体模量权重越大.由路面结构荷载响应分布云图(见图9)可知，路基内部压应变空间分布函数就能够满足上述要求.因此，可尝试使用路基内部单元最大压应变作为权函数，由此确定路基的当量回弹模量.其合理性可以通过与当量回弹模量反算值的比较进行验证.

具体加权方法如下：导出路基区域所有单元质心处的模量Ei和压应变的绝对值εzi，根据压应变指标进行加权.表达式为

(10)

2 结果及分析

本节将分别列出不同浸水水位时，路面响应和路基回弹模量的变化规律，并进行数值分析.若无特殊说明，以下涉及的应变结果均为荷载作用峰值时刻所对应单元的最大主应变.

2.1 路面响应结果

图11为面层层底拉应变和路基顶面压应变与水位的关系曲线.

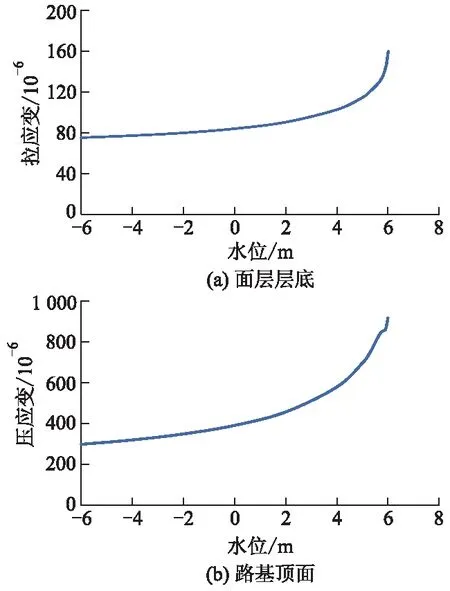
图11 拉应变、压应变与水位的关系曲线

由图11a可知：面层层底拉应变随水位的抬升，变化规律类似指数变化；当水位位于地下(水位为0 m以下)时，变化量较小，水位从-6 m上升至0 m，拉应变增加了11.6%；当水位位于地上时，此时路基部分出现饱和区，拉应变变化明显，水位从0 m上升至5 m，拉应变增加了36.3%；当水位升至5 m以上时，拉应变迅速增加，水位为5～6 m时，拉应变增加了39.3%.

由图11b可知：路基顶面压应变的变化规律与拉应变类似，当水位为-6～0，0～5，5～6 m时，压应变分别增加了30.8%，77.4%和31.6%.可见，低水位时，压应变的变化幅度较拉应变更为明显；而高水位时，面层的拉应变能够更好地反映路基受浸水水位的影响.

高水位情况下，路面结构应变增长迅速的原因可能是受到超孔隙水压力的影响.图12给出了水位分别为0，6 m时荷载峰值对应的孔隙水压力分布云图.由于路面荷载作用时间相当短，FWD荷载加载到峰值仅需0.015 s，另外，路基填土材料的渗透系数相当小，为5×10-7m·s-1.因此，在路基内积聚的超孔隙水压力无法在如此短暂的时间内消散，有效应力进一步缩小，从而导致土体的回弹模量减小.然而，在路基水位不高时，土体饱和区位于较深的位置，路面荷载传递到饱和区时只引起少量超孔隙水压力，并且深处土体的模量对选取的两个最大应变值贡献较小.而路基上部区域存在一定高度的非饱和区，该区域本质上至少为土、水、气三相结构，非饱和区土体受压时，土孔隙内的气体会优先散逸，不会引起超孔隙水压力积聚.当然，由于ABAQUS中假设土体空气压力与外部大气压相同，土内气体受压时可以自由移动，自然就没有超孔隙气压力的说法.

图12 水位为0，6 m时荷载峰值的孔隙水压力分布

综上可知，由于路基内部水位抬高对路面结构力学响应的影响是明显的.当水位上升时，沥青层底拉应变增大可能引起沥青面层材料过早出现疲劳破坏，路基顶面压应变增大可能引起路面车辙的出现，这些情况都会影响路面的使用性能，缩短其使用寿命.

2.2 路基当量回弹模量结果

采取1.5节所述的两种方法计算路基当量回弹模量，结果如图13所示.图13a为通过拉应变和压应变两种指标迭代反算模量的结果，可以看出两种指标反算时，由于选用指标不同，两条曲线的模量值在同一水位时有所差异，但二者表现出的趋势类似.路基模量均随水位上升而显著减小，变化范围为20～190 MPa，线性相关系数分别为0.986 7和0.978 3，基本可认为服从线性变化.

图13b比较了迭代反算与加权计算的结果，依据的指标均为路基顶面压应变.由图可知，加权计算结果与更为精确的迭代反算结果具有较高的一致性，因此可认为通过压应变的分布加权计算路基回弹模量的方法是可行的.

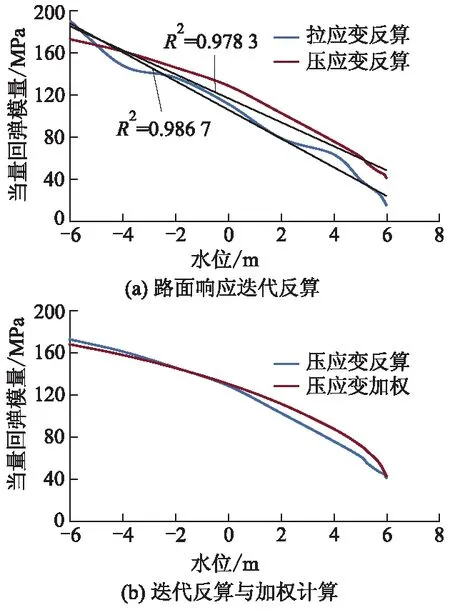
图13 不同方法路基当量回弹模量结果比较

总之，两种方法确定路基当量回弹模量值均表现出了强烈的湿度相关性.这也意味着在实际路面结构设计中，应该重视路基湿度的影响.首先，在确定路基回弹模量时，应该考虑实际路基的湿度情况；其次，当路基湿度过高时，应该采取必要的防排水措施.笔者介绍了两种当量回弹模量的确定方法，迭代反算法虽然过程比较繁琐，但计算结果较为精确；加权计算法较为简单，但是权函数的确定是其重难点所在.两种方法均为路基回弹模量值的选取提供了一种思路.后续可以针对不同的路基材料、路面结构等因素进行敏感性分析，提供可参考的路基湿度取值范围.

3 结 论

建立了路面结构在多种水位下的ABAQUS有限元模型，得到了水位不断抬升时FWD荷载下的结构响应，并通过迭代反算和加权计算的方法，得到对应的回弹模量，最后通过对比分析得到了路面响应和路基回弹模量随水位的变化规律.结论如下：

1)水位的抬升对面层层底拉应变和路基顶部压应变的影响是明显的，其变化趋势类似指数变化.工程中，可以考虑设置路基隔断层或路基防水设施，以减少路面结构可能产生的永久变形.

2)低水位时，路基顶面压应变的变化更为明显，而在水位抬升至路基接近饱和时，面层层底拉应变变化更为明显.实际上，水位抬升至路基顶面的情况极少，所以在浸水路基设计中，路基顶面压应变的指标尤为重要.

3)采用迭代反算和加权计算确定的路基当量回弹模量均与路基湿度具有较强的相关性，路基模量随着水位上升基本呈线性减小的趋势.

4)依据FWD荷载作用下压应变的分布进行加权计算的结果与更为精确的迭代反算结果具有较高的一致性.因此，可以认为根据压应变的分布对路基回弹模量进行加权计算的方法是可行的.