不均衡闸瓦压力作用重载机车轮轨动态行为

曹云强，刘鹏飞，张凯龙，刘红军，高昊

不均衡闸瓦压力作用重载机车轮轨动态行为

曹云强，刘鹏飞，张凯龙，刘红军，高昊

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

为研究不均衡闸瓦压力对重载机车轮轨动态行为的影响，以我国实际运营中HXD型六轴重载机车为研究对象，在多体动力学软件UM中建立综合考虑多种非线性力学关系重载机车模型，将制动过程考虑仅有闸瓦压力作用。仿真结果表明：在直线运行条件下紧急制动状态时，当1位轮对出现不均衡制动故障，对重载机车动态行为影响最甚，此时1位轮对横移量、摇头角均是最大幅值，1位轮对较其他轮对，轮对横移量、摇头角最大分别增加46.97%和86.73%；车辆过曲线时分别在1位内轮、3位外轮正常制动工况下，对车辆动态行为影响较大，且各考核工况同样以1位轮对响应最为剧烈。由此可见, 端位轮对在所有可能出现故障的轮对中安全隐患较大，故障时出现轮缘贴靠的可能性更大。

重载机车；动态行为；多体动力学；不均衡闸瓦压力；制动故障

闸瓦制动是铁路机车常用的制动形式，其制动性能稳定发挥直接关系到列车的制动安全性。但长久以来，制动系统发生故障似乎成为常态，其中机车单元制动器制动力的不正常作用已成为典型故障。例如，洛阳铁路办事处曾发现，SS6型电力机车因轮对蛇行运动及通过曲线造成闸瓦与车轮踏面接触不良，机车一度出现闸瓦偏磨现象[1]，徐州北机务段曾通过检修发现，5台DF8B型机车中就有7个单元制动器发生不制动故障[2]。而近年来，在HXD2C型电力机车上又出现了单元制动器不缓解故障问题,加剧了踏面磨耗，同时闸瓦贴靠处踏面还出现金属夹渣[3]，另外单元制动器悬挂连杆断裂等故障[4]也成为重载机车运营过程中频频出现的问题。针对制动条件下列车的运行安全性，魏伟等[5−6]以2万t重载组合列车为研究对象，研究了重载列车制动系统与纵向动力学等联合仿真系统，对2万t重载组合列车在实际运营中列车运行的安全性提供了重要的参考价值以及理论依据；王开云等[7−8]研究了制动工况下，车钩系统纵向作用力对重载机车与轨道系统的动态相互作用；阳光武等[9]建立车体载荷方程，研究了机车车体在两端车钩制动力作用下对机车直线运行安全性的影响；刘鹏飞等[10−11]建立并验证了重载列车-轨道耦合动力学模型，研究在紧急制动工况下列车纵向冲击及车辆轮轨动态相互作用。同时Durali等[12]在紧急制动工况下对列车脱轨的安全性进行了相应分析研究； Wislon等[13]讨论了在制动条件下列车运行安全的评判标准；MA等[14]建立重载机车短编组分析模型，研究了车钩及缓冲器系统对重载机车动力学性能的影响，对列车在制动过程中可能出现的脱轨情况进行了分析；QU等[15]研究了机车在制动条件下，车钩和缓冲器系统对机车动力学性能及运行安全性的影响；GAO等[16]建立重载列车纵向动力学数值模型，对紧急制动过程中车钩装置纵向力进行了分析研究；ZOU等[17]模拟了紧急制动工况下车钩的动态响应及其对机车的运行安全性影响。上述相关研究着重于闸瓦压力及制动力的均衡施加条件，尚未考虑机车车辆各车轮制动力不均衡作用问题。但无论单元制动器的制动缓解不良，亦或是制动器不动作，还是闸瓦与踏面接触不良，均会造成机车各车轮制动力的不均衡问题，由此带来的轮对运行姿态变化及轮轨运行安全性问题尚未引起重视，鲜见相关报道，需进一步探讨。鉴于此，本文以六轴重载机车为研究对象，建立车辆动力学模型，以典型的直线、曲线运动为考核，主要针对闸瓦制动发挥最大效能的条件下，模拟单个轮对一侧单元制动器完全失效，另一侧制动器正常制动的极限工况状态，分析在单纯闸瓦压力作用下的动态行为，重点关注同一转向架不同轮对产生不均衡闸瓦压力后，哪个轮对的动态性能恶化最严重，以此来揭示最基本的动态行为规律，并讨论闸瓦压力不均衡程度对机车动态行为的影响规律。

1 机车模型建立与仿真工况设置

1.1 机车动力学建模及闸瓦压力确定

以25 t轴重六轴重载机车为研究对象，根据部件运动关系构建机车动力学模型总体拓扑结构，如图1所示。在此基础上，参考文献[18]，利用UM多体动力学分析软件，建立车辆动力学仿真分析模型。模型中将轨道模型考虑为无质量轻型钢轨，机车建模考虑电机(轴悬式)、电机吊杆、轴箱的点头运动，牵引杆考虑3个自由度(伸缩、横摆、沉浮)，轮对、构架及车体等机车主要结构组成考虑6个自由度，总计84个自由度，并且同时考虑中间轮对自由横动量、一系垂向减振器、二系横向减振器等关键非线性力学关系环节，同时根据文献[19]中HXD型六轴重载机车具体参数进行建模，图2所示为六轴重载机车模型(模型坐标系参照UM中，和空间坐标系，整车模型转向架分为Ⅰ和Ⅱ 两端)。

列车制动的过程是一个非常繁琐复杂的过程，图3给出了UM中施加闸瓦压力建模，建模过程忽略闸瓦接触角的影响，将闸瓦压力简化为一个集中力，只取紧急制动过程中极限工况即闸瓦贴靠踏面时闸瓦压力最大情况，为了简化计算便于模型的仿真，参考文献[20]中实算闸瓦压力，单个闸瓦压力为

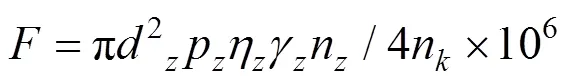
式中：各参量的含义及取值在表1中列出，部分数值参考文献[21−22]，经计算每个制动单元踏面闸瓦压力为F=51.92 kN。

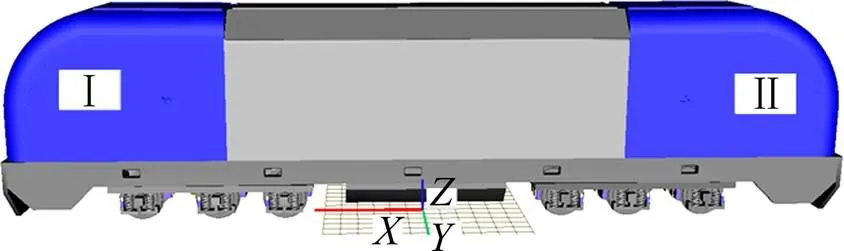
图2 整车动力学模型坐标系

表1 实算闸瓦压力参数

图3 闸瓦压力建模

1.2 模型验证

参照文献[19]中计算条件及实测数据，对模型的准确性进行对比验证，试验及仿真线路条件：直线100 m，缓和曲线70 m，曲线半径300 m，曲线长160 m，超高120 mm；轨道激励选择了我国干线轨道不平顺作为激扰，选用60 kg/m钢轨，JM3标准踏面，轨底坡1/40 m，运行速度70 km/h，惰行工况。如图4所示，给出了1和6位轮对轮轨垂向力及轮轨横向力的对比分析，结果表明：仿真分析模型计算结果较为准确合理，轮轨垂向力及轮轨横向力幅值及变化规律与实测结果基本吻合，误差在可接受范围内，可以进行下一步的仿真分析。

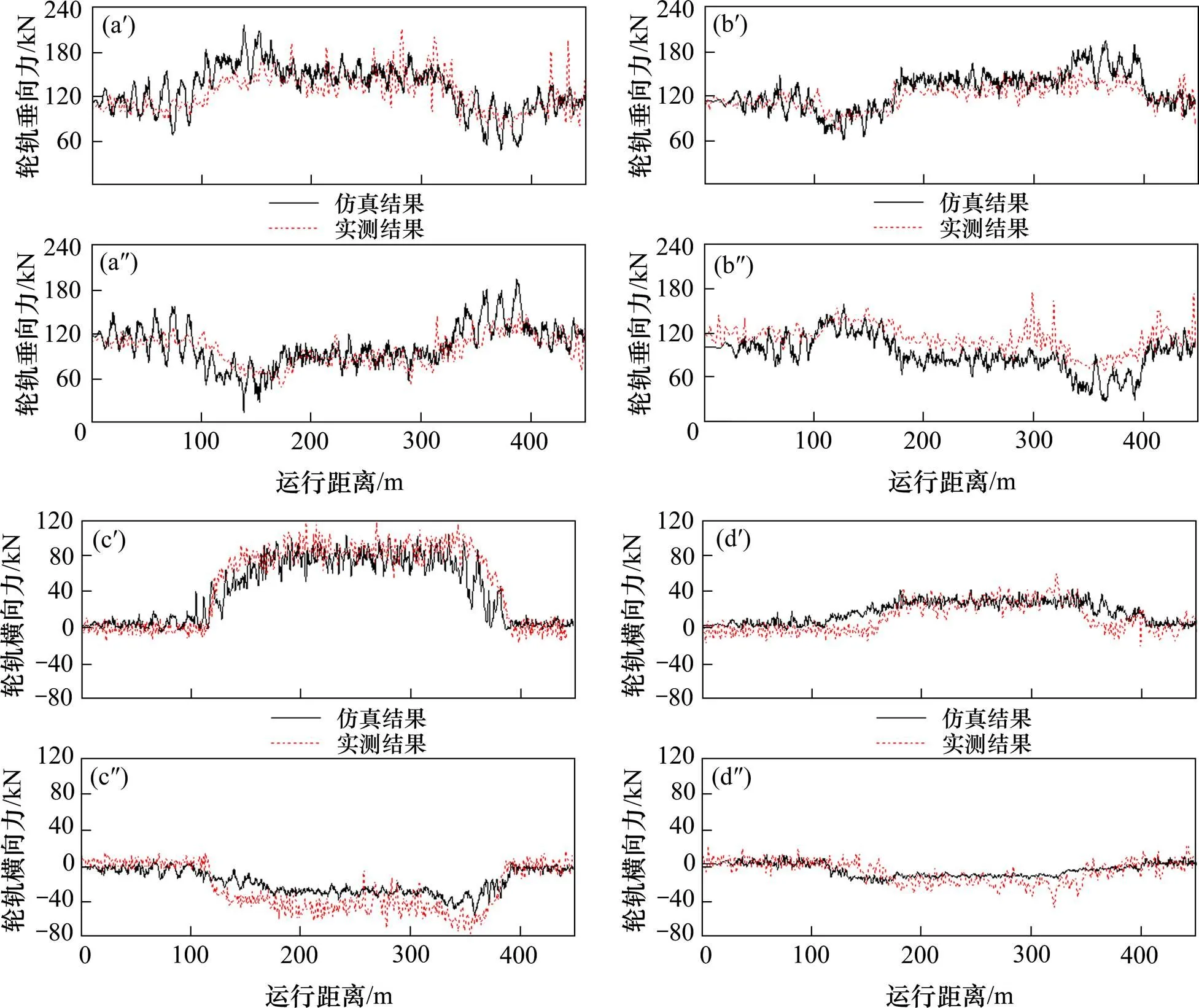
(a′), (a″) 1位轮轨垂向力；(b′), (b″) 6位轮轨垂向力；(c′), (c″) 1位轮轨横向力；(d′), (d″) 6位轮轨横向力

1.3 不均衡闸瓦压力作用计算工况设置

以此六轴重载机车动力学模型，模拟运行过程中机车可能出现的制动故障，图5给出了三轴转向架侧置式单元闸瓦制动装置安装分布示意，左右侧闸瓦制动器对称布置。由于机车在直线运行时左右侧受力状态具有对称性，因此本文以转向架轮对左轮制动缸全部失灵，即右轮施加闸瓦压力而左轮闸瓦压力为0来模拟制动故障状态。为反映不均衡闸瓦压力的影响规律和作用效果，仿真过程并未施加轨道激励，闸瓦力施加方式如图6所示，图中FLx，FRx分别表示第位轮对左、右侧车轮所受闸瓦压力的大小。

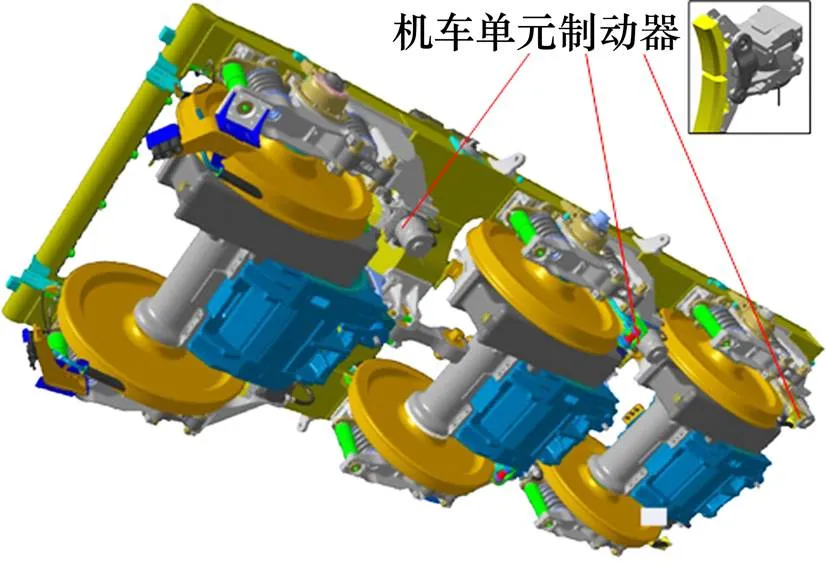
图5 三轴转向架单元制动器布置

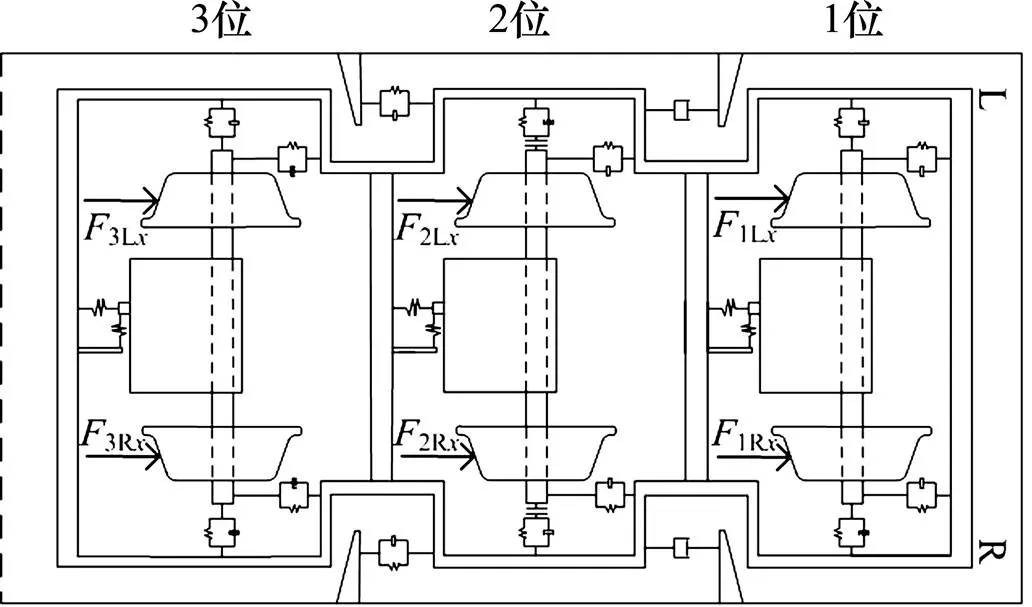
图6 闸瓦压力施加模拟方案

仿真方案选取各轮对左轮发生制动故障，只有右轮制动，并选取机车紧急制动时的运行状态，此时闸瓦压力将达到最大，同时机车前后转向架对称布置，故只需前转向架各轮对施加闸瓦压力，计算工况设置如表2所示。

表2 计算工况

同时等间隔以10 kN为差值，工况1，2和3施加的闸瓦压力依次递减(闸瓦压力从51.92 kN减至1.92 kN)，设置仿真分析方案，得到不同闸瓦压力作用下动态行为最大幅值统计，以此研究在不同闸瓦压力作用下对轮对动态行为的影响程度。

2 运动姿态机理分析

下面从蠕滑理论角度，说明闸瓦压力改变轮对运行状态的基本原理。当对轮对外侧施加一个闸瓦压力Lx时(在轮对内侧施加闸瓦压力同外侧机理一致仅受力方向相反)，轮对会产生一个顺时针方向的正向力矩，首先以弹性约束单轮对为例，如图7所示，考虑其静平衡条件下的受力状态和动作过程。当轮对承受顺时针力矩时，轮对势必相应产生一个正向摇头角w，由轮轨蠕滑理论可知，轮轨横向蠕滑力(横向蠕滑系数为22)与摇头角满足式(2)，因此作用于轮对上的合成横蠕滑力F为正向，推动轮对正向移动，产生位移w，之后由于踏面具有锥度，右轮滚动半径增大，左轮滚动半径减小(车轮名义滚动半径为0)，左、右轮对间形成式(3)给出的纵向蠕滑力(纵向蠕滑系数为11)，且其合成的蠕滑力矩与力矩方向相反，纵向蠕滑力矩的逐渐增大直至与力矩相互抵消，轮对才达到新的平衡状态，当轮对为弹性约束状态时，蠕滑力矩与弹性约束力矩将同时作为反力矩以抵消力矩。

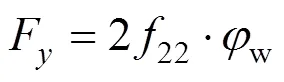
(3)

3 直线运行状态下轮对运动分析

3.1 不同工况条件下轮对横移响应对比分析

为了对比同一个转向架不同轮对产生不均衡闸瓦压力后，确定动态性能恶化最严重工况，本节根据上述计算工况分析不同轮对上施加闸瓦压力的轮对横向运动状态。

图8给出了不均衡闸瓦压力施加在1位右轮时所有轮对横移动态行为，由图8可见，在紧急制动状态下闸瓦压力为51.92 kN时，1，2，3位轮对横移量分别为5.94，3.15和4.03 mm，1位轮对横移量分别比2和3位横移量大46.97%，32.15%，闸瓦压力对Ⅱ端所有轮对横移量基本无影响，且4和6位轮对横移量幅值基本一致为0.17 mm，5位轮对横移量幅值为0.20 mm。Ⅰ端所有轮对横移量随着闸瓦压力的增大而增大，但增幅依次减小，当闸瓦压力从1.92 kN增至51.92 kN时，相应的轮对横移量整体增幅为：1位5.90 mm，2位3.10 mm，3位4.02 mm，Ⅱ端轮对的横移动态响应则几乎不受闸瓦压力改变而发生明显变化。

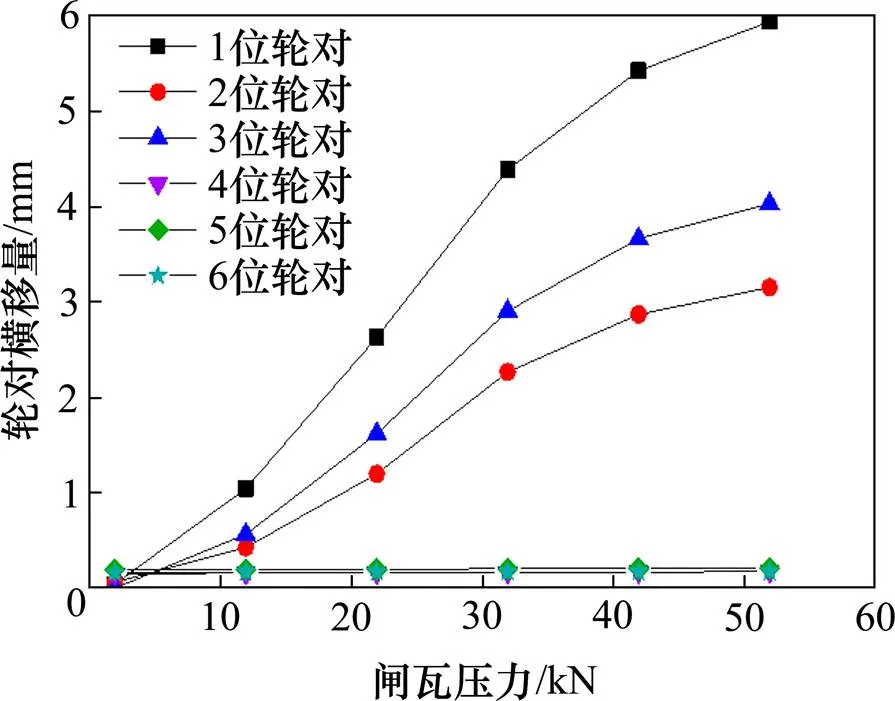
图8 工况1条件下轮对横移动态行为

在工况1条件下，Ⅰ端1位轮对横移量最大，存在较大的安全隐患，同时Ⅱ端轮对响应很小几乎可以忽略不计，故下文着重研究Ⅰ端轮对并分析其动态行为规律。

图9反映了不均衡闸瓦压力施加在2位右轮时，不同闸瓦压力作用下横移最大值统计结果，由图9可以看出，闸瓦压力为51.92 kN时2位轮对横移量幅值最大达4.90 mm，1和3位轮对横移量幅值分别为0.74 mm和0.50 mm，与2位轮对相比，1和3位轮对横移量基本可以忽略不计，且1位轮对横移方向与2和3位轮对横移方向相反；同时2位轮对横移量随着闸瓦压力的增大而增大，且增幅尤为明显，1和3位轮对横移动态响应受闸瓦压力改变的影响很小，轮对横移量均在1 mm以下。

图10给出了不均衡闸瓦压力施加在3位右轮时，不同闸瓦压力作用下横移量最大值统计结果，根据图10可知，紧急制动状态下1和2位轮对横移量幅值较大，幅值分别为5.71 mm和5.04 mm，3位轮对横移量较小幅值为1.18 mm，且随着闸瓦压力的增大Ⅰ端所有轮对横移量均呈现出增大的趋势，且由于1和2位横移量较大，在此激扰下轮缘贴靠的可能性大大增加。

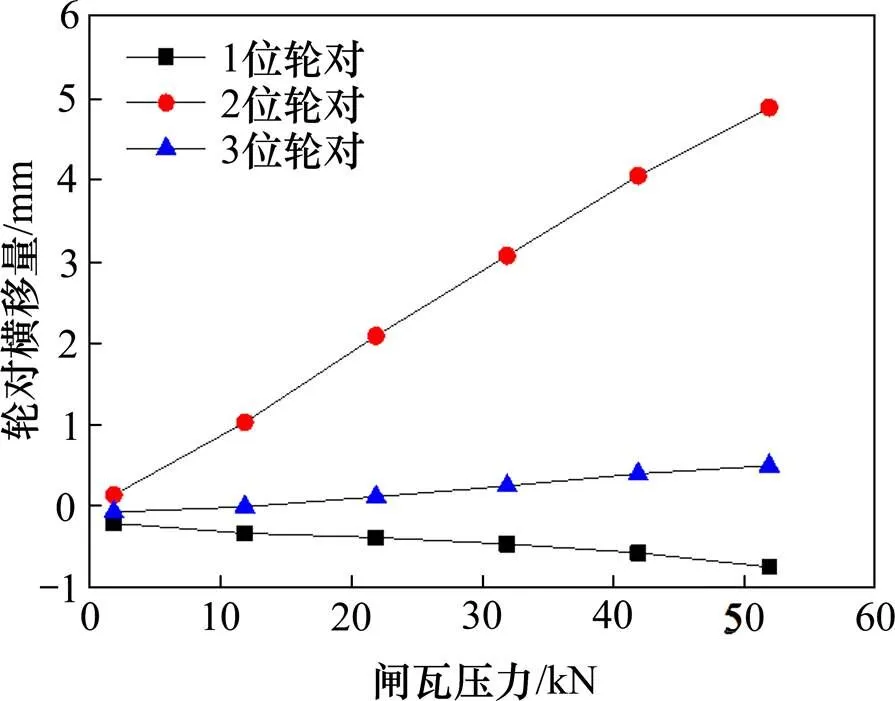
图9 工况2条件下轮对横移动态行为

图10 工况3条件下轮对横移动态行为

因此，当不均衡闸瓦压力施加在1位右轮时各轮对横移响应最明显，且以1位轮对横移量最大，幅值为5.94 mm，存在较大安全隐患，故下文着重分析工况1条件下摇头运动状态，以此反映在安全隐患最大工况下，摇头响应动态行为规律。

3.2 最严重工况下轮对摇头响应分析

本节分析轮对摇头动态响应，给出随闸瓦压力改变摇头角幅值变化规律，得出不均衡闸瓦压力对摇头运动影响程度。

图11反映了摇头角动态行为响应规律，由图11可知，在紧急制动状态下Ⅰ端各轮对摇头角幅值依次分别为9.8×10−4，2.1×10−4和1.3×10−4rad，不均衡闸瓦压力施加在1位右轮上，故1位轮对摇头角动态响应最为剧烈，其幅值较2和3位轮对摇头角分别大78.57%和86.73%；且Ⅰ端所有轮对随闸瓦压力的增大，幅值均有明显增加，1位轮对摇头角响应随闸瓦压力的改变更为敏感，摇头角的变化速率更快，1位轮对与2和3位轮对摇头方向相反，与1位轮对相比较2和3位摇头角的增长速率敏感性有很大降低。

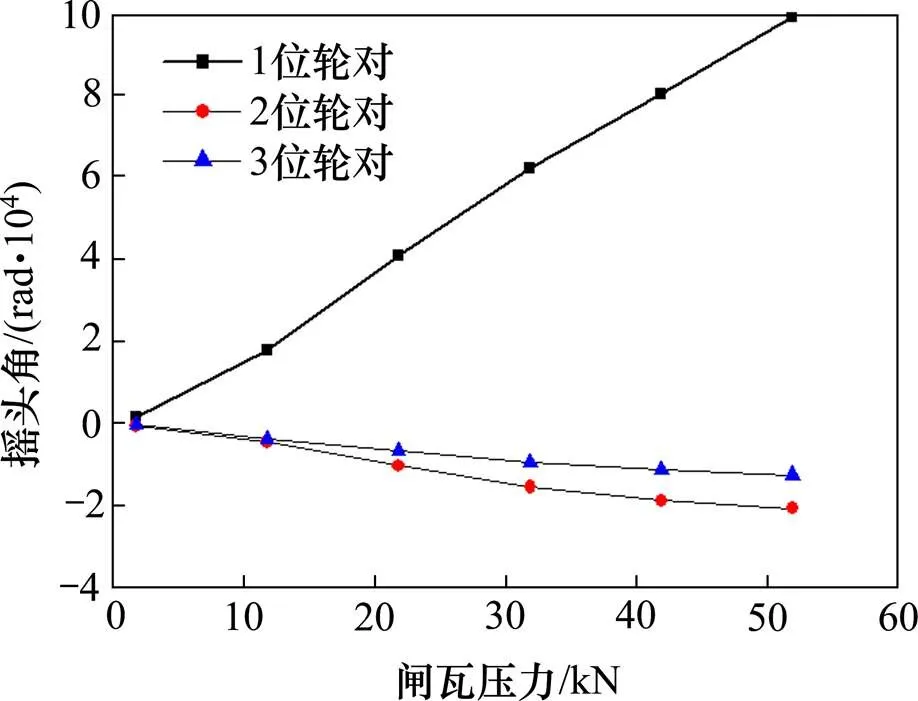
图11 摇头动态行为

通过对轮对横移量、摇头角在不同闸瓦压力作用下幅值变化规律分析不难发现，制动时闸瓦压力对轮对运动姿态影响，以故障端转向架响应最为剧烈且以端位轮对发生故障时，受闸瓦压力变化最明显，其轮对横移量以及摇头角动态行为响应更甚，潜在安全隐患较大。

4 曲线通过轮对横移响应分析

根据前文所述，在直线运行状态下，产生不均衡闸瓦压力作用，1位轮对运动状态最为剧烈，无轨道激励条件下，轮对横移、摇头响应均呈强相关表现，车辆存在较大潜在安全隐患。本节给出了车辆过曲线时，前文所述各工况下轮对横移动态响应，轮对摇头运动这里不在赘述，同时对应增加不同轮对内轮制动失效，外轮正常制动工况，以此对比曲线通过时，内外轮闸瓦制动分别失效时轮对横移响应的变化规律，根据文献[23] 中已有重载铁路设计规范要求，仿真线路条件设置为：曲线半径800 m，曲线200 m，直线100 m，缓和曲线70 m，超高120 mm，速度90 km/h。

图12给出了内、外轮分别在闸瓦压力作用下，轮对横移动态响应幅值变化规律，从图12(a)可知，紧急制动状态下，Ⅰ端转向架只有1位内轮发挥制动作用时，横移响应为最剧烈工况，1位轮对横移量最大达10.39 mm，且随着闸瓦压力的增加，1，2和3位轮对同样呈现增大的趋势，Ⅱ端转向架各轮对，对闸瓦压力改变横移响应没有明显变化；从图12(b)可以看出，在紧急制动状态下，Ⅰ端转向架在3位外轮发挥制动作用时对车辆横移运动影响较大，此工况下1位轮对同样为横移响应最剧烈轮对，横移幅值达10.21 mm，但轮对横移量随闸瓦压力的增大改变量甚小，基本可以忽略不计。

(a) 内轮施加不均衡闸瓦压力横移响应；(b) 外轮施加不均衡闸瓦压力横移响应

通过对曲线运行状态下机车轮对横移响应计算分析可知，所有考核工况中，以1位内轮、3位外轮制动器发挥制动作用时，对机车运行状态影响较大，且同样可以得出，曲线通过时不均衡闸瓦压力的大小改变对无故障端转向架动态响应变化影响甚微。

5 结论

1) 制动过程中六轴重载机车Ⅰ，Ⅱ端转向架，在同一个转向架中，两侧端位任意一端(即1位与6位轮对)出现闸瓦压力不均衡制动故障时，对出现故障转向架影响最甚，而对另一端无故障转向架影响很小。

2) 直线运行状态下，当端位轮对出现不均衡制动故障时，轮对横移动态响应较为明显，紧急制动时工况1计算条件下,1位轮对横移量幅值已经达到5.94 mm，与其他轮对相比潜在安全隐患更大；在不均衡闸瓦压力作用制动过程中，随着踏面闸瓦压力的增大，轮对横移量、摇头角均随之增大。

3) 机车以制动状态通过曲线，不同轮对外侧、内侧制动器失效时，2种条件下，1位、3位轮对处制动故障对机车动态行为影响最明显，一致表现为1位轮对横移达到最大。

[1] 黄鹏飞, 王国建. 电力机车闸瓦偏磨的原因及其处理[J]. 机车电传动, 2000(3): 46. HUANG Pengfei, WANG Guojian. Causes and handing for bias-wearing of braking-shoe of electric locomotive[J]. Electric Drive for Locomotive, 2000(3): 46.

[2] 张英勇. 单元制动器不制动故障的原因分析和防止措施[J]. 铁道机车车辆工人, 2003(9): 6−9. ZHANG Yingyong. Cause analysis and preventive measures for non-brake failure of unit brakes[J]. Railway Locomotive ＆ Rolling Stock Workers, 2003(9): 6−9.

[3] 王国建. HXD2C型机车单元制动器不缓解故障原因分析及对策[J]. 电力机车与城轨车辆, 2012, 35(4): 85−86. WANG Guojian. Cause analysis of brake unit device un-release of braking fault and countermeasure on type HXD2C locomotive[J]. Electric Locomotives ＆ Mass Transit Vehicles, 2012, 35(4): 85−86.

[4] 王雪萍, 张军, 朱黄石, 等. 机车用单元制动器悬挂连杆的断裂问题分析[J]. 北京建筑大学学报, 2018, 34(2): 55−59. WANG Xueping, ZHANG Jun, ZHU Huangshi, et al. Analysis of fracture problem of suspended connecting rod in locomotive unit brake[J]. Journal of Beijing University of Civil Engineering and Architecture, 2018, 34(2): 55− 59.

[5] 魏伟, 赵连刚. 两万吨列车纵向动力学性能预测[J]. 大连交通大学学报, 2009, 30(2): 39−43. WEI Wei, ZHAO Liangang. Prediction of longitudinal dynamic coupler force of 20000 ton connected train[J]. Journal of Dalian Jiaotong University, 2009, 30(2): 39− 43.

[6] 魏伟, 张东芹, 张军. 重载列车纵向冲动机理及参数影响[J]. 大连交通大学学报, 2011, 32(1): 1−6. WEI Wei, ZHANG Dongqin, ZHANG Jun. Study of longitudinal impulse mechanism and parameters impact of heavy haul train[J]. Journal of Dalian Jiaotong University, 2011, 32(1): 1−6.

[7] 王开云, 翟婉明. 纵向压力作用下重载机车与轨道的动态相互作用[J]. 西南交通大学学报, 2009, 44(1): 7− 12. WANG Kaiyun, ZHAI Wanming. Dynamic interaction between heavy locomotive and track under longitudinal force of coupler[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 7−12.

[8] 王开云, 翟婉明, 封全保, 等. 重载机车车钩自由角对轮轨动态安全性能的影响[J]. 中国铁道科学, 2009, 30(6): 72−76. WANG Kaiyun, ZHAI Wanming, FENG Quanbao, et al. Effect of coupler free angle on wheel/rail dynamic safety performance of heavy haul locomotive[J]. China Railway Science, 2009, 30(6): 72−76.

[9] 阳光武, 肖守讷, 马卫华. 制动力对机车直线运行安全性的影响[J]. 西南交通大学学报, 2010, 45(5): 657−662. YANG Guangwu, XIAO Shoune, MA Weihua. Effect of coupler compression force on locomotive safety on tangent track[J]. Journal of Southwest Jiaotong University, 2010, 45(5): 657−662.

[10] 刘鹏飞, 王开云, 翟婉明. 驱动工况下重载机车与轨道动态相互作用[J]. 西南交通大学学报, 2014, 49(1): 15− 20. LIU Pengfei, WANG Kaiyun, ZHAI Wanming. Dynamics interaction between heavy-haul locomotive and track under driving conditions[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 15−20.

[11] 刘鹏飞, 王开云, 张大伟. 牵引及制动操纵对重载机车轮轨动力作用的影响[J]. 中国铁道科学, 2017, 38(2): 96−104. LIU Pengfei, WANG Kaiyun, ZHANG Dawei. Influence of traction and braking operation on wheel-rail dynamic interaction for heavy haul locomotive[J]. China Railway Science, 2017, 38(2): 96−104.

[12] Durali M, Shadmehri B. Nonlinear analysis of train derailment in severe braking[J]. Journal of Dynamic Systems, Measurement, and Control, 2003, 125(1): 48− 53.

[13] Wilson N, Fries R, Witte M, et al. Assessment of safety against derailment using simulations and vehicle acceptance tests: A worldwide comparison of state-of-the- artassessment methods[J]. Vehicle System Dynamics 2011; 49(7): 1113–1157.

[14] MA W, LUO S, SONG R. Coupler dynamic performance analysis of heavy haul locomotives[J]. Vehicle System Dynamics, 2012, 50(9): 1435−1452.

[15] QU Tianwei, MA Weihua, WU Dong, et al. Influence of coupler and buffer on dynamics performance of heavy haul locomotive[J]. Open Mechanical Engineering Journal, 2015, 9(1):1033−1038.

[16] GAO Guangjun, CHEN Wei, ZHANG Jie, et al. Analysis of longitudinal forces of coupler devices in emergency braking process for heavy haul trains[J]. Journal of Central South University, 2017, 24(10): 2449−2457.

[17] ZOU R, LUO S, MA W. Simulation analysis on the coupler behaviour and its influence on the braking safety of locomotive[J]. Vehicle System Dynamics, 2018, 56(11): 1−21.

[18] ZHAI W, WANG K, CAI C. Fundamentals of vehicle– track coupled dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1349−1376.

[19] 翟婉明, 刘鹏飞, 王开云, 等. HXD2C重载机车一系参数调整前后的动力学性能分析[R]. TTRI−2011−01, 成都: 西南交通大学列车与线路研究所, 2011. ZHAI Wanming, LIU Pengfei, WANG Kaiyun, et al. Dynamic performance analysis of HXD2C heavy haul locomotive before and after primary parameter adjustment[R]. TTRI−2011−01, Chengdu: Institute of Trains and Lines, Southwest Jiaotong University, 2011.

[20] 邹瑞明. 组合式重载列车中部机车运行安全性研究[D].成都: 西南交通大学, 2015. ZOU Ruiming. Research on the running safety of middle locomotive of combined heavy haul train[D]. Chengdu: Southwest Jiaotong University, 2015.

[21] 周浩, 张齐, 于海霞. HXD2型大功率交流传动电力机车制动能力分析[J]. 铁道机车车辆, 2008, 28(增1): 251−253. ZHOU Hao, ZHANG Qi, YU Haixia. HXD2 high-power electric locomotive brake capability analyzing[J]. Electric Locomotives & Mass Transit Vehicles, 2008, 28(Suppl 1): 251−253.

[22] 闫剑. 机车踏面制动器试验系统研究[D]. 成都: 西南交通大学, 2015. YAN Jian. Research on test system for tread brakes of the locomotive[D]. Chengdu: Southwest Jiaotong University, 2015.

[23] TB 10625—2017, 重载铁路设计规范[S]. TB 10625—2017, Code for design of heavy haul railway[S].

Wheel-rail dynamic behavior of heavy-haul locomotive under asymmetric brake shoe pressure

CAO Yunqiang, LIU Pengfei, ZHANG Kailong, LIU Hongjun, GAO Hao

(School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In order to study the influence of unbalanced brake-shoe pressure on the dynamic behavior of heavy-haul locomotive wheel track, the typical HXD six-axle heavy-haul locomotive in Chinese actual operation was taken as the research object. The heavy-haul locomotive model was established in the multi-body dynamics software UM with a comprehensive consideration of various nonlinear mechanical relationships. The results show that the dynamic behavior of the heavy-haul locomotive was more affected when the 1st wheelset had an unbalanced braking fault in straight line running condition emergency braking state. At this time the 1st wheelset transverse-quantity, the yaw angle were all the maximum amplitudes. Compared with other wheelsets, the maximum transverse-quantity and yaw angle of 1st wheelset increased by 46.97% and 86.73%, respectively. When the vehicle passed the curve, it had a large impact on the dynamic behavior of the vehicle under the normal braking conditions of 1st inner wheel or 3rd outer wheel. Under these two conditions, the dynamic behavior of the vehicle was greatly affected, and the 1st wheelset response was also the most severe in each assessment condition. It can be seen that the 1st (6th) wheelset had a large safety hazard in all possible failure wheelsets and the wheel flange was more likely to close when the fault occurs.

heavy-haul locomotive; dynamic behavior; multibody dynamics; asymmetric brake shoe pressure; brake failure

10.19713/j.cnki.43−1423/u.T20190927

U270.1

A

1672 − 7029(2020)07 − 1808 − 09

2019−10−21

国家自然科学基金青年基金资助项目(51605315，11790282)；河北省自然科学基金面上资助项目(E2018210052)

刘鹏飞(1986−)，男，山西大同人，副教授，博士，从事机车车辆动力学研究；E−mail：lpfswjtu@163.com

(编辑 阳丽霞)