基于ARIMA模型的高铁浮动票价与票额分配优化方法

姚加林，皮珊

基于ARIMA模型的高铁浮动票价与票额分配优化方法

姚加林，皮珊

(中南大学 交通运输学院，湖南 长沙 410075)

针对我国铁路单一的票价体系和确定性票额分配方式问题，探索高铁列车票价与票额的综合优化方法；依据时间序列分析原理，考虑客流的随机性，构建ARIMA客流预测表达式，将该表达式嵌入Log-Linear需求与价格的函数关系式中，结合票价制定规则、列车定员等约束，构建以铁路运输收益最大为目标的高铁列车浮动票价与票额分配综合优化模型；以G13列车为例进行计算分析，算例结果表明该模型能提高铁路运输收益，为高铁票价与票额的综合优化提供一定参考依据。

ARIMA模型；客流量预测；Log-Linear需求函数；浮动票价

目前，铁路运输主要采用单一的票价体系，即以一定的客票票价率，采取递远递减的形式确定。而铁路客票分配则是基于确定性的票额分配方式，一般按照担当局长途旅客优先的原则进行初期分 配[1]。单一的票价体系与确定性的票额分配方式缺乏整体协同性，既不能对市场做出有效的判断，也不能很好地提高铁路运输收益。因此铁路运输票价与票额的综合优化问题也成为铁路运营管理领域的热点研究问题之一[2]。国内外专家学者对票价、票额问题做了大量研究，刘帆洨等[3]通过对同一时期不同区间的旅客购票需求强度进行研究，提出了非线性回归支持向量机的预测模型，以天为单位对区间内旅客购票需求进行预测。Ciancimino等[4]研究了票额为确定型需求下的线性票额分配模型。William[5-6]等研究了基于乘客行为的席位控制策略，并与基于客流预测的控制策略进行对比，分析2种策略的优缺点。Ongprasert[7]从运输效益出发，考虑列车上座率以及旅客公平性，构建铁路运输效益模型。赵翔等[8]研究了不同列车多种停站方案的票额分配问题。张旭等[9]研究了民航竞争影响下高速铁路多等级定价动态差别定价模型。胡万欣等[10]通过分析高速铁路与民航运输之间的博弈关系，构建了一个以社会福利最大为上层目标，高铁、民航企业效益为下层目标的双层规划模型。但是这些研究都是独立进行，没有将票价与票额结合起来，缺乏整体协同性。因此，学者们开始考虑研究票额与票价的综合优化问题。YOU[11]在客流预测的基础上研究多级票价的制定问题。赵翔等[11]研究了高速列车折扣票价与票额分配组合优化模型。宋文波等[13]基于收益管理理论，结合高铁运输组织的特点，研究了高速铁路单列车动态定价与票额分配综合优化模型。上述票价与票额的综合优化研究成果中，对于客流的需求多假设服从正太分布或者泊松分布，对客流需求的随机性考虑不足。此外，上述研究成果大多采用效用函数来表示客流量与票价之间的关系，而该函数灵敏度难以估计，且参数的选择与确定需要大量样本。为此，本文运用时间序列分析法，将客流量分类为具有规律性和季节性的客流量(确定项)和随机客流量(随机项)，采用ARIMA模型拟合得到客流预测表达式，引入Log-Linear指数需求函数来表达票价与票额之间的函数关系，结合票价制定、列车定员要求等各类约束，构建基于ARIMA模型的高铁列车浮动票价与票额分配的综合优化模型，并以京沪高铁G13次列车为例进行计算分析。

1 模型构建

1.1 问题描述

高速铁路运输是一个具有多OD，多区段的复杂运输网络，本文重点研究单列车的浮动票价与票额分配问题。图1表示某列车的运行径路，从始发站a出发，经过中间停靠站b和c，到达终点站d。高铁列车浮动票价与票额分配就是依据各OD旅客在不同票价下对于运输的需求，充分利用列车席位能力进行各OD票额分配，最终使铁路运输收益达到最大的目的。

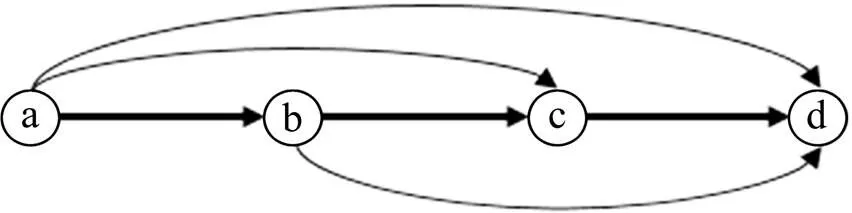
图1 列车运行径路

1.2 需求函数参数和预测表达式的确定

在经济学中，一种商品的需求是指消费者在一定时期内在各种可能价格水平下，愿意而且能够购买的该商品数量。而需求函数则表示一种商品的需求数量和影响该需求数量的各种因素之间的相互关系，是一个多元函数[14]。本文中所涉及的票额即为需求，票价即为价格。

常用表示价格与需求的函数有线性需求函数、指数需求函数和logit需求函数。而指数函数中的Log-Linear函数的需求值恒为正数，因此无需考虑需求的取值而对票价范围进行额外的约束。基于此考虑，本文采用Log-Linear需求函数来描述需求与价格之间的关系，Log-Linear需求函数的一般表达式为：

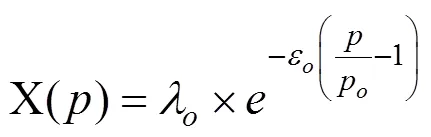
其中：表示需求密度；表示价格弹性，反映一定时期内当一种商品的价格变化1%时所应引起的该商品需求量变化的百分比。p表示实际票价，通过12306铁路官方售票软件查询可知，表示高铁定价。

考虑到本文研究的是单位时间(1 d)内票额需求量与高铁票价之间的函数关系，因此将该表达式中需求密度用需求期望值(x)代替计算，而需求期望值(x)则采用ARIMA模型预测得出，改造后的需求函数表达式为：

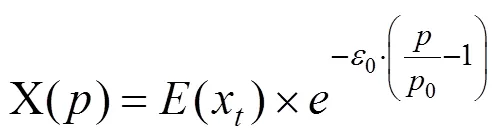
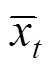
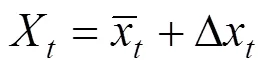
1.3 浮动票价与票额分配综合优化模型

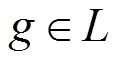
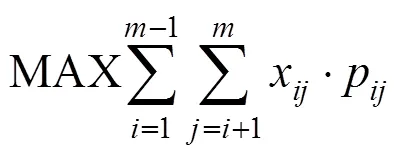
其中：x表示列车在区间()的票额分配数；p表示列车在()区间的定价；A表示区间OD占用情况，为0-1变量，列车占用区间()取值为1，否则为0；C表示列车在区间()的能力约束，即列车定员数；而p表示OD各区段票价之和；p表示OD任意一区段票价。式(4)表示列车定员约束；式(5)表示票价和票额的函数关系，(X)为区间()用ARIMA客流量预测得出的票额期望值，p表示某区间实际票价，表示OD间票价的价格弹性系数；式(6)表示票额的整数约束；式(7)表示票价的浮动范围；式(8)表示组成该OD的各分区段运价之和大于该OD的票价，式(9)表示该OD票价要大于组成此OD的票价之和减去任一区段票价，2式一起表示票价制定中递远递减的规则。

2 ARIMA模型求解

在进行ARIMA模型拟合前，首先需对原始序列进行分析，判断序列是否规律性变化以及是否为长期增长趋势。其次，依据时间序列分析原理可知，序列的前后数据之间存在时间上的相依性，因此在进行模型拟合时应当选取同一趋势的相连数据。传统时间序列模型是将随机项纳入预测误差范围，由于预测误差范围波动较大，本文将随机客流纳入ARIMA预测模型中。

差分自回归移动平均模型(ARIMA模型)是将非平稳的时间序列进行差分平稳化后，结合模型确定规则，构建合适的时间序列模型并进行预测分析的方法，一般记作：ARIMA(,,)，其中为自回归项，为差分项，为移动平均项。

以G13次列车2015年客票销售数据为例进行分析，确定预测表达式，具体方法步骤如下：

Step 1：分析原始序列是否具有的季节变化规律及长期增长趋势，若没有，则不适合使用时间序列分析法。

首先对各OD进行客流分析，由图2可知，G13次列车运输旺季在寒暑假2个时期，运输淡季在5月和9月，存在季节性规律且客流量总体呈增长的趋势。

Step 2：检验原始序列的平稳性。若原始序列不平稳，则需要进行差分处理，并再次进行平稳性检验，直至序列平稳。

对G13次高铁2015年票额销售的分析可知，该序列波动较大(图3所示)，需要做差分处理，使数据平稳化，该序列经过一阶差分处理后为平稳时间序列(图4)，此时该序列值为1。

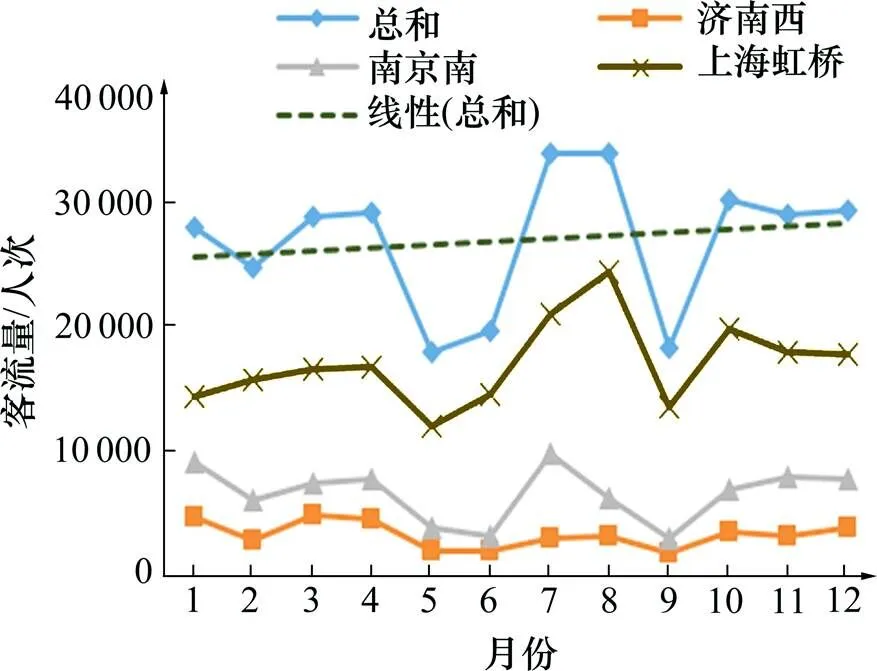
图2 G13次列车2015年各月客流量

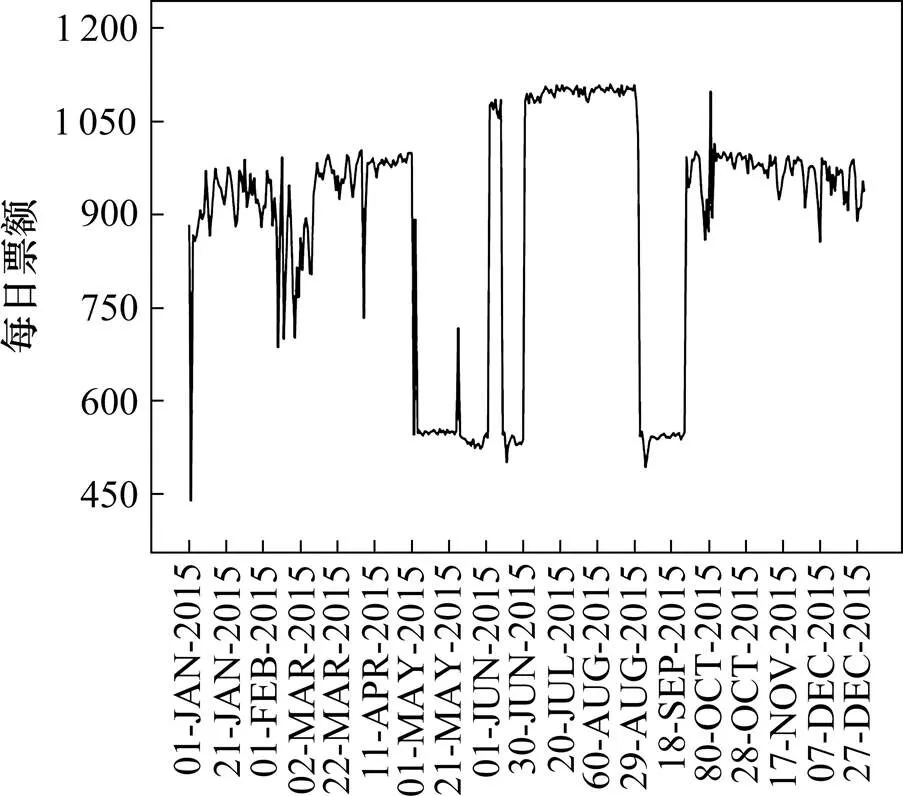
图3 客票销售原序列

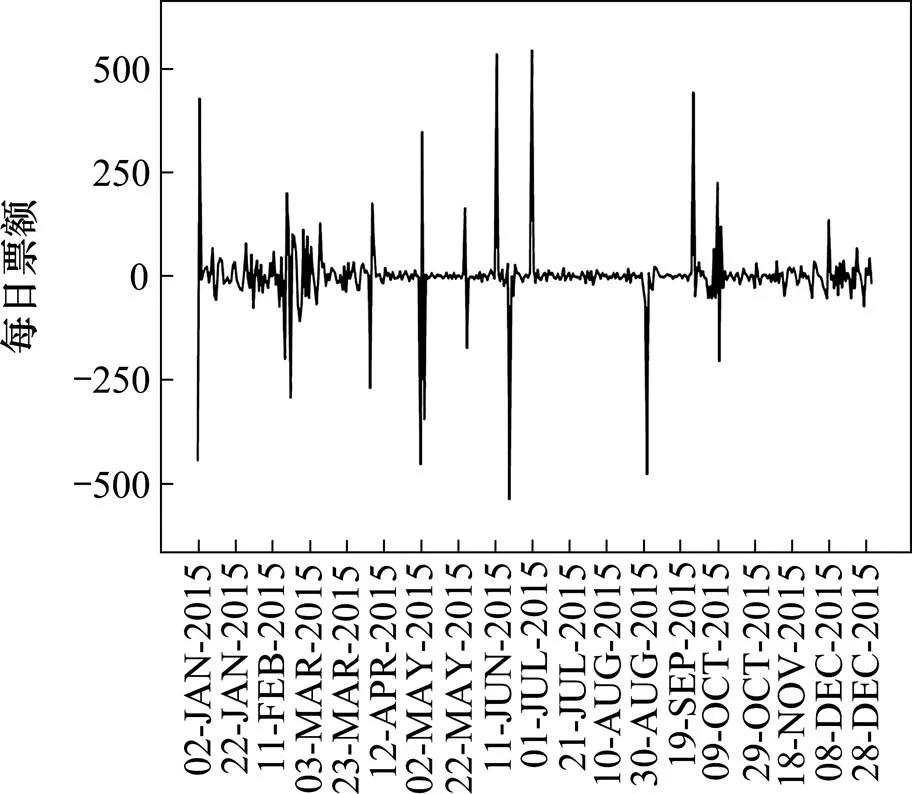
图4 一阶差分序列

Step 3：模型识别与参数估计。利用SPSS软件进行拟合，通过自相关函数(ACF)图和偏自相关函数(PACF)图，分析ACF和PACF截尾或拖尾的情况：若序列的PACF是截尾，而ACF是拖尾，则序列选取AR模型；若PACF是拖尾，而ACF是截尾，则序列选取MA模型；若PACF和ACF均是拖尾，则序列选取ARMA模型。再结合选取BIC最小系数原则，最终确定和值。

截取G13次列车北京南−上海虹桥区段2015年6~8月数据，利用SPSS软件进行进一步拟合，预测。最终得到的自相关函数(图5)和偏自相关函数(图6)，差分后的序列ACF呈一步截尾，PACF呈一步截尾。最终拟合结果显示为ARIMA(0,1,1)的BIC系数最小为7.978，移动平均系数为0.193，常数项为6.169。因此可知确定项的表达式为：

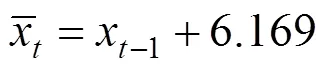
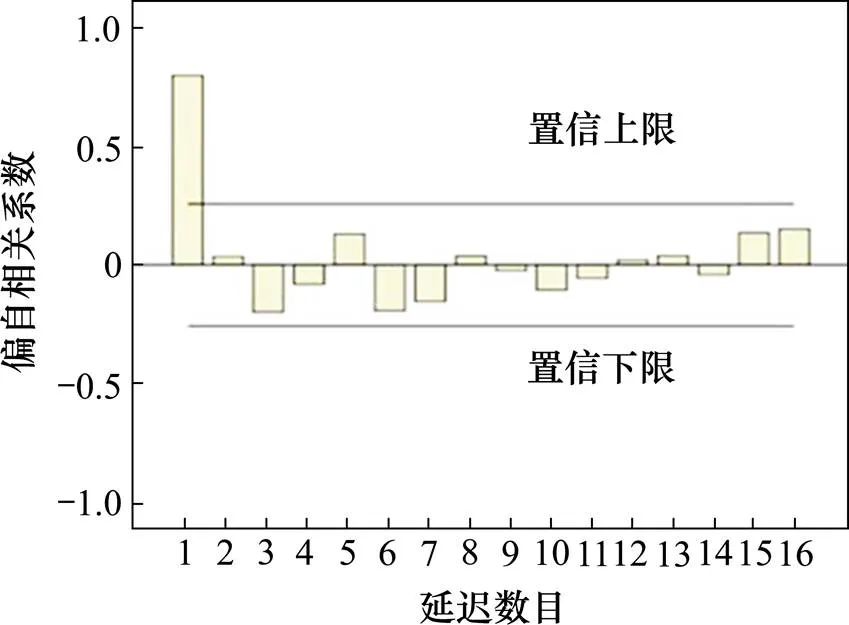
图6 偏自相关函数图

Step 4：假设检验。判断残差的自相关函数(ACF)图和偏自相关函数(PACF)图，若为白噪声序列，则模型通过检验，同时，对残差分布进行拟合，确定其分布函数的各项参数。G13列车残差拟合分布为图7所示。

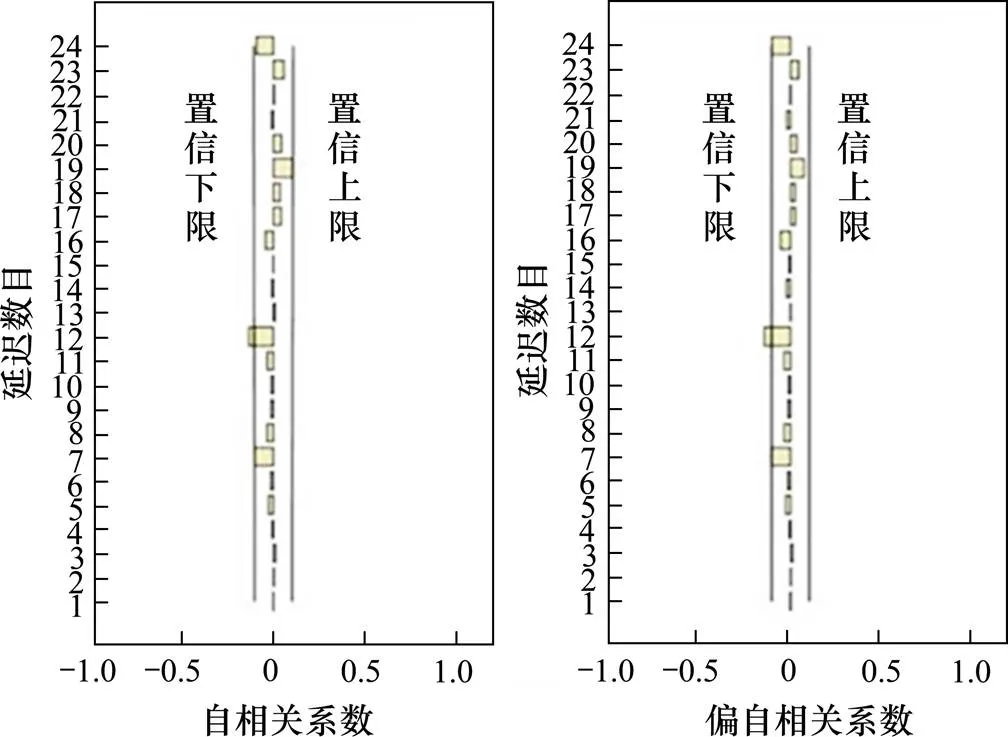
图7 残差自相关函数和偏自相关函数图

最终拟合的随机项符合均值为−0.25，标准差为1.604的正态分布。因此随机项的表达式为：

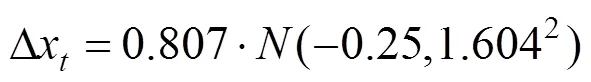
Step 5：预测分析。确定客流预测的基本表达式(同式(3))。

综上可知，G13次列车北京南−上海虹桥区段的客流量预测模型为：

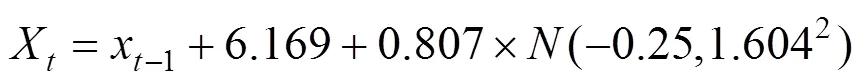
关于利用SPSS统计分析软件对ARIMA模型拟合的详细过程参见文献[15−16]。

3 案例分析

以京沪线上2015年北京南至上海的G13次列车为例计算，该列车的运行线路上有4个客运站，分别为北京南、济南西、南京南和上海虹桥。G13次列车2等座定员871人。列车票价以2等座票价为基础，上浮动值为5%，下调10%，四舍五入取值，如表1所示。

G13次列车各OD间客流量预测表达式依照第2节中所介绍的预测方法同理得出，同时，基于该表达式计算出8月1日各OD间预测客流量，如表2所示。

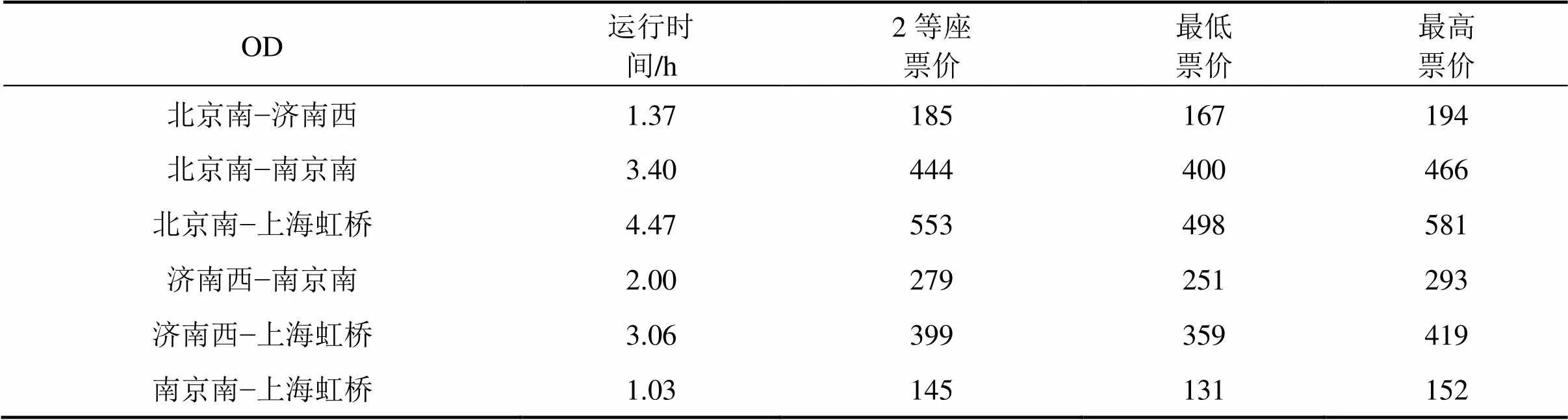
表1 G13次列车票价及票价调整范围

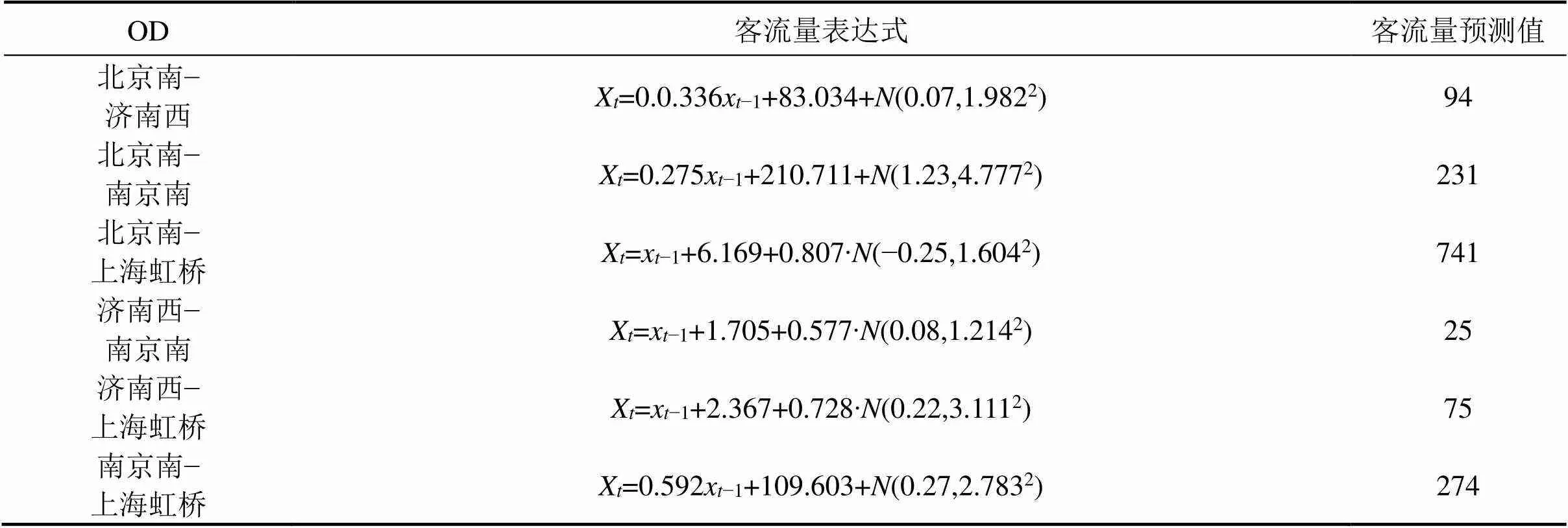
表2 G13次列车客流量预测表达式

各OD间需求弹性系数参考文献[17]取值，如表3所示。

运用Lingo软件进行编程求解，得到票额分配和最终定价结果。总收益为494 297元。从表4可以看出，G13次列车总收益对比没进行浮动票价措施的情况增长了3.79%；客座率在优化后达到98.06%，列车运能得到充分利用；北京南−南京南和南京南−上海虹桥区段的客票分配较少，客流满足率低，一方面是因为本文的目标函数是各区段收益总和最大，而北京南−济南、济南西−南京南2个区段的收益(169+293=462元)大于北京南−南京南的收益(400元)。另一方面，票额分配满足长途优先原则，且南京南−上海虹桥的需求的价格弹性较小，因此在分配方式上优先考虑了弹性较大的长途区段，将票额分配给了北京南−上海虹桥和北京南−济南西2个区间，最终得到表4的分配方案。

表 3 需求弹性系数

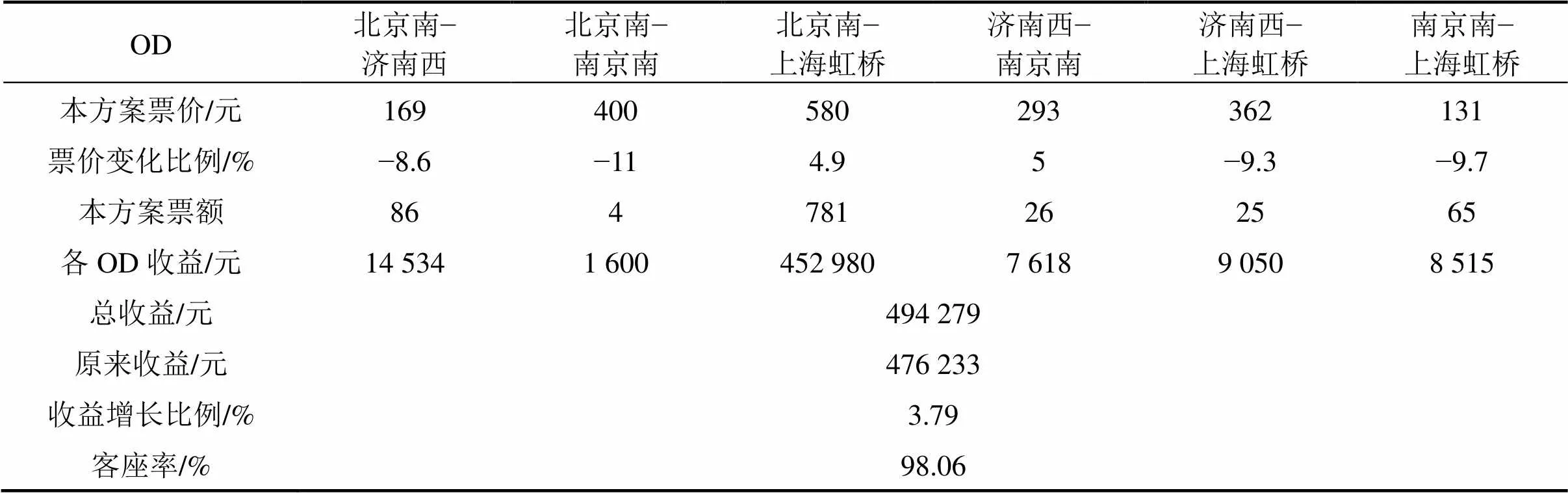
表 4 最终优化方案

4 结论

1) 结合时间序列理论与Log-Linear需求函数，考虑客流量的随机性，构建一个高铁列车浮动票价与票额分配综合优化模型；将客流分类为确定性客流和随机性客流，建立ARIMA预测表达式，引入Log-Linear需求函数，结合票价制定、票价浮动范围、列车定员等各约束，运用lingo软件计算出铁路运输收益最大的票价和票额分配方案。

2) 以列车G13为例，用本文的方法进行计算分析，优化后客座率达98.06%，运输收益提高了3.79%。本文研究对象主要为单列车，今后在不断的运输实践过程中将进一步研究多列车以及全路的综合优化模型。

[1] 韩潇. 铁路客运运价问题研究[J]. 铁道运输与经济, 2001, 23(7): 9−10. HAN Xiao. The research on railway passenger transport price problem[J].Railway Transportation and Economy, 2001, 23(7): 9−10.

[2] 李建海. 高速铁路票价优化研究[D]. 成都: 西南交通大学, 2016. LI Jianhai. The research on ticket price optimization of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2016.

[3] 刘帆洨, 彭其渊. 铁路旅客购票需求预测模型研究[J].交通运输工程与信息学报, 2018, 16(2): 50−56. LIU Fanxiao, PENG Qiyuan. Forecasting model for railway passenger ticketing demand[J]. Journal of Transportation Engineering and Information, 2018, 16(2): 50−56.

[4] Ciancimino A, Inzerillo G, Lucidi S, et al. A mathematical programming approach for the solution of the railway yield management problem[J]. Transportation Science, 1999, 33(2): 168−181.

[5] William L Cooper. Asymptotic behavior of an allocation policy for revenue management[J]. Operations Research, 2002, 50(4): 720−727.

[6] Joern Meissner, Arne Strauss. Improved bid prices for choice-based network revenue management[J]. European Journal of Operational Research, 2012, 217(2): 417−427.

[7] Ongprasert S. Passenger behavior on revenue management systems of inter-city transportation[D]. Japan: Kochi University of Technology, 2006.

[8] 赵翔, 赵鹏, 李博. 多列车多停站方案条件下高速铁路票额分配研究[J]. 铁道学报, 2016, 38(11): 9−15. ZHAO Xiang, ZHAO Peng, LI Bo. Research on high- speed railway ticket allocation under condition of multiple trains and multiple trains stop plans[J]. Journal of the China Railway Society, 2016, 38(11): 9−15.

[9] 张旭, 陈秉智, 李振福, 等. 民航竞争影响下高速铁路动态差别定价研究[J]. 铁道学报, 2017, 39(10): 19−25. ZHANG Xu, CHEN Bingzhi, LI Zhenfu, et al. Study on dynamic differential pricing for high-speed rail under influence of competition from civil aviation[J]. Journal of the China Railway Society, 2017, 39(10): 19−25.

[10] 胡万欣, 操杰, 张艳. 市场化环境下的高速铁路与民航客运博弈定价优化[J]. 大连交通大学学报, 2016, 37(4): 14−19. HU Wanxin, CAO Jie, ZHANG Yan. Game pricing optimization model of high speed train and aviation in transport market[J].Journal of Dalian Jiaotong University, 2016, 37(4): 14−19.

[11] YOU P S. An efficient computational approach for railway booking problems[J]. European Journal of Operational Research, 2006, 185(2): 811−824.

[12] 赵翔, 赵鹏, 姚向明, 等. 高速列车折扣票价与票额分配组合优化模型[J]. 东南大学学报(自然科学版), 2018, 48(4): 759−765. ZHAO Xiang, ZHAO Peng, YAO Xiangming, et al. An integrated optimization model of discount fare and ticket allocation for high-speed train[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(4): 759− 765.

[13] 宋文波, 赵鹏, 李博. 高速铁路单列车动态定价与票额分配综合优化研究[J]. 铁道学报, 2018, 40(7): 10−16. SONG Wenbo, ZHAO Peng, LI Bo. Research on comprehensive optimization of dynamic pricing and seat allocation for high-speed single train[J]. Journal of the China Railway Society, 2018, 40(7): 10−16.

[14] 胡金荣, 刘堂发. 微观经济学[M]. 北京: 人民邮电出版社, 2015. HU Jinrong, LIU Tangfa. Microeconomics[M]. Beijing: People Post Press, 2015.

[15] 宇传华. SPSS与统计分析[M]. 北京: 电子工业出版社, 2007. YU Chuanhua. SPSS and statistical analysis[M]. Beijing: Electronic Industry Press, 2007.

[16] 李庆扬, 关冶, 白峰杉. 数值计算原理[M]. 北京: 清华大学出版社, 2000. LI Qingyang, GUAN Ye, BAI Fengshan. Principle of numerical calculation[M]. Beijing: Tsinghua University Press, 2000.

[17] 郑金子. 高速铁路票价动态优化方法的研究[D]. 北京:北京交通大学, 2017. ZHENG Jinzi. Research on ticket fare dynamic optimization method for high-speed railway[D]. Beijing: Beijing Jiaotong University, 2017.

The optimization method of floating ticket price and ticket allocation of high-speed railway based on ARIMA model

YAO Jialin, PI Shan

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

This paper aims to explore the comprehensive optimization method of high-speed railway fare and ticket amount for the single fare system of China’s railway and deterministic ticket amount allocation in China. Based on the principle of time series analysis, this paper considered the randomness of passenger flow, constructs the ARIMA passenger flow prediction expression which embed in the Log-Linear demand and price function. And a comprehensive optimization model for floating fares and ticket allocation of high-speed railway single trains with the maximum benefit of railway transportation was constructed. Taking G13 train as an example, the calculation results show that the model can improve the railway transportation revenue and provide a reference for the comprehensive optimization of high-speed rail fare and ticket amount.

ARIMA model; passenger flow forecast; Log-Linear demand and price function; floating fares

10.19713/j.cnki.43−1423/u.T20190882

U2-9

A

1672 − 7029(2020)07 − 1655 − 07

2019−10−11

国家自然科学基金面上资助项目(71471179)

姚加林(1961−)，男，湖南娄底人，副教授，从事交通运输规划与管理等研究；E−mail：yaojialn@csu.edu.cn

(编辑 阳丽霞)