基于数据场聚类的拉林铁路隧道施工风险评估

张欢，郝伟，顾伟红

基于数据场聚类的拉林铁路隧道施工风险评估

张欢，郝伟，顾伟红

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

为了明确高寒地区复杂的施工环境以及恶劣的气候条件对拉林铁路隧道施工带来的风险所属等级，提出一种基于数据场聚类的隧道施工风险评估模型。针对拉林铁路隧道工程的施工特点，分析隧道施工主要的施工风险与固有风险，构建符合拉林铁路地质特征的隧道施工风险评价指标体系。使用模糊评语集对风险指标进行风险概率和风险损失描述，对描述结果进行定量转化后，用基于数据场的高斯混合模型聚类确定各风险因素等级。运用该模型对位于拉林铁路的巴玉隧道施工风险进行评价，并与传统的K-means聚类结果进行比较，证明高斯混合模型的评价结果更加精准。

拉林铁路；隧道施工；施工安全；数据场；聚类分析；高斯混合模型

目前川藏铁路的建设受到了社会各界的关注，川藏铁路的顺利通车，对我国西部经济的快速发展和民族团结具有重大意义。然而高海拔和特殊气候带来的复杂环境和地质问题对川藏铁路的修建带来了众多挑战[1−2]。拉林铁路作为川藏铁路的重要组成部分，位于青藏高原东南部，海拔在2 800~ 3 700 m之间。山高谷深，气候极端恶劣，是典型的高寒地区地貌。拉林铁路段计划修建隧道47座，桥隧比高达70%以上[2]，因此隧道施工安全受到了建筑行业及学术界的重视。在此之前学者们也对隧道施工安全做了大量的研究。张东明等[3]以超前地质预报体为基础，利用模糊层次评价方法建立了深埋长隧道的地质灾害风险评估体系。顾伟红等[4]采用基于熵权的模糊综合评估模型对铁路隧道TBM 施工关键风险进行评估。郭发蔚等[5]利用贝叶斯网络对隧道施工的各风险事件所属等级进行评估。魏立伟等[6]采用模糊网络分析法构建了典型隧道施工安全风险评价模型。目前针对高寒地区独有的环境与地质条件进行隧道施工风险评估的研究较少，并且多数研究停留在数学计算建立评价模型，对当代信息社会日渐火热的大数据平台与人工智能平台的利用程度不够，未能很好地处理风险评估的随机性与不确定性；有些研究注重整体的风险等级评估，忽略了不同风险源的评价，不利于后期开展专项风险评估，而高寒地区隧道施工风险专项评估是必不可少的。基于此，本文提出基于数据场聚类的拉林铁路隧道施工风险评估模型[7]。传统的专家打分法在对指标进行评价的时候具有主观性强的特点，并且由于参与专家人数多且涉及领域的区别，只简单求取平均值作为指标分值的传统方法过于片面，因此本文采用模糊评语集对风险事件进行描述，充分考虑风险事件对应风险级别的模糊性与不确定性，并且对不同的专家根据其知识经验赋予相应的权重，从而使评价数据更具有代表性。而数据场可以填补数据不完备所带来的缺陷，直观的体现数据与数据之间的联系，便于后期的专项风险评估与应对[8]。

1 隧道施工风险评价指标体系

1.1 风险评价标准的构建

风险评价标准的合理划分有利于后期对各指标的风险评估及对不同等级风险的专项应对，因此本文参考《铁路隧道风险评估与管理暂行规定》中的风险度量与评价标准，并在其基础上进行完善，采用相应的定性语言描述风险，并对不同风险等级给定数域，将定性语言转化成定量描述，可以将隧道施工安全评价等级划分为以下5个等级。具体划分见表1。

表1 评价等级标准

1.2 评价指标体系的构建

拉林铁路隧道工程具有工程规模大，施工难度高，施工环境恶劣等特点，受复杂的环境与地质条件影响，在施工的过程中存在很多潜在危险源。不少地段同时面临着活动断裂、滑坡崩塌、高热高温、高地应力等诸多地质难题[9]。本文参考《铁路隧道风险评估与管理暂行规定》、《铁路隧道工程施工技术指南》[10]及《川藏铁路沿线及邻区环境工程地质问题概论》[11]等相关规范及文献，结合拉林铁路隧道工程的实际施工特点，并在充分征询现场施工技术专家与高校学者意见的基础上，根据系统性、目标性、全面性原则，制定相应的施工风险评价指标体系，如表2所示。

1.3 模糊评语集及其转化

1.3.1 定义评语集

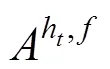
1.3.2 指标评语的转化

专家(=1=1,2,…,)依据自己的知识和经验针对不同风险因指标模糊评语h进行选择评价，得到专家指标评语统计结果，并按照式(1)计算各风险指标的广义隶属度。

由于不同专家之间有一定的知识和经验差距，给出的指标评语在一定程度上也存在着不可靠性，基于此，本文根据各专家职称和项目经验赋予相应的指标权重，使评价结果更具有可靠性。参与问卷调查的专家一共有10位，如表4。

表2 隧道施工风险评价指标体系

表3 模糊评语集定义

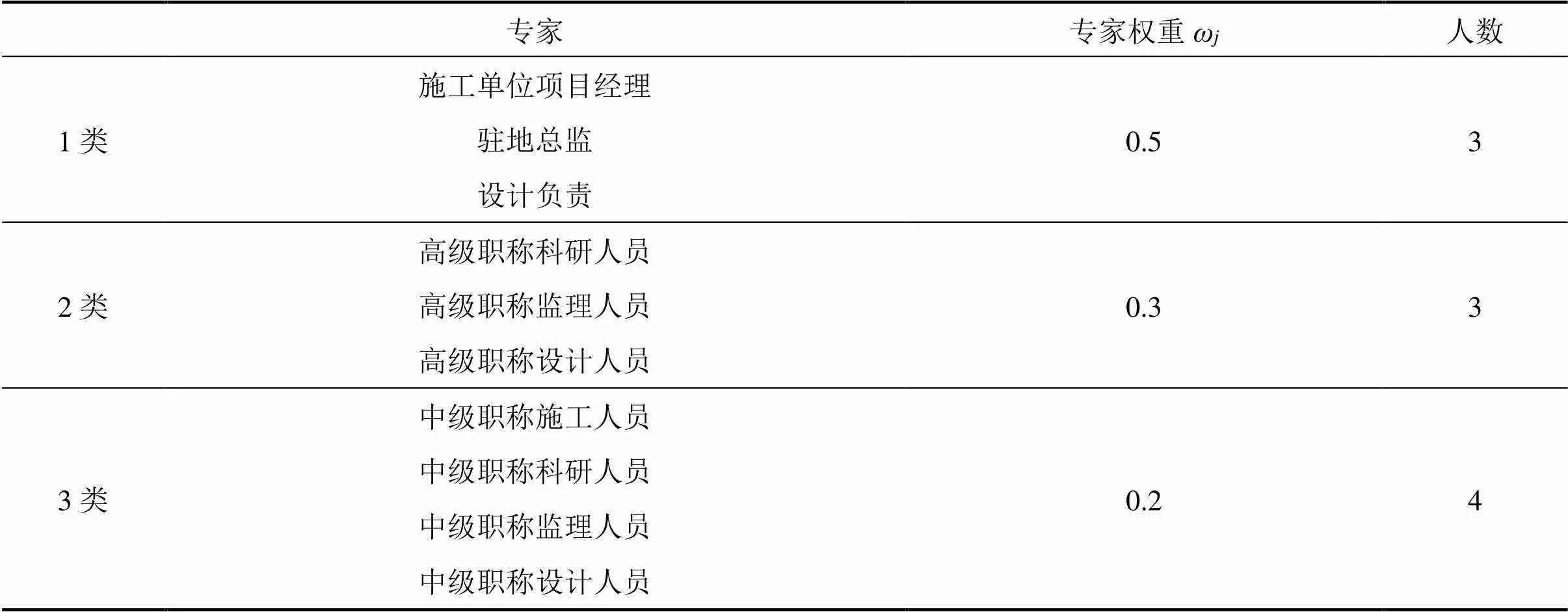
表4 专家权重分配

综合考虑了专家权重后的广义隶属度为：

2 高斯混合模型

所谓高斯混合模型(Gauss Mixture Mode，GMM)[13]是指对数据样本的概率密度分布进行估计，以几个高斯模型的加权作为估计模型。每个高斯模型就代表了一个类，因此模型数量要在模型训练之前确定。

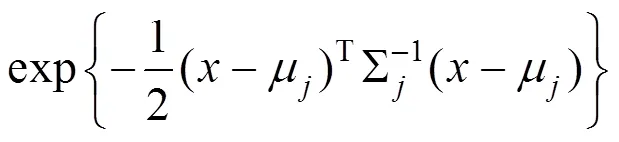
假设有个高斯分布，以一定的概率混合，则得到了高斯混和模型，即：

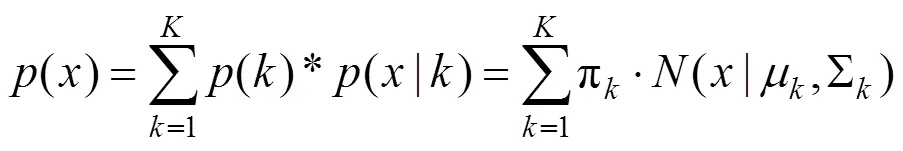
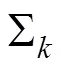
高斯混合模型的概率密度函数为：

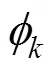
GMM通常采用EM(Expectation Maximum)算法[14]对GMM 参数进行估计。算法流程为：

1) 初始化参数

2) E-step

令的后验概率如式(6)所示。

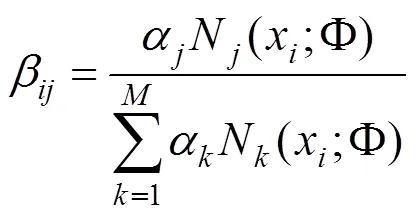
3) M-step

更新权值得：

更新均值得：

更新方差矩阵：

4) 收敛条件

3 高斯混合模型的改进

由以上可知，传统的高斯混合聚类模型只能对聚类簇数已知的样本进行评价，而这些实际操作中往往无法确定，这也是传统EM算法最大的不足[15]。基于此，本文提出了用数据场对EM算法进行改进。引入数据场思想，计算出每个数据对象的势值，势值越大的数据对象，说明其受其他数据点共同作用越大，另一个侧面反映该点周围的数据点越多，该点就有可能成为聚类中心，因此可以以势值极大点作为样本的聚类中心，而势值极大点的分类个数就是聚类个数。

基于数据场改进的高斯混合聚类模型综合了人工智能与数据挖掘的优点，一方面具有对不全面的数据进行补充的优势，另一方面可以有效的检索风险之间的关联性并将其进行分类，并利用计算机运算代替了传统的人工数据计算过程，是土木工程领域当前发展的一个新方向。

3.1 数据场的建立

场的概念最早是由英国的物理学家法拉第提出来，表示一种传递物体间的非接触相互作用的媒介[16]。李德毅根据物理学中的场论思想，将物质粒子间的相互作用及其场描述方法引入抽象的数域空间，提出数据场的概念。

如果把每个样本的观测向量看作是一个数据点，那么个样本就构成了维特征空间里的个数据点。设存在于空间里的每个数据点周围都存在一个作用场，且受到其他对象的联合作用，这样就在空间里确定了数据集的数据场[17]。引入势函数描述数据场的属性时，空间任一点的势值为：

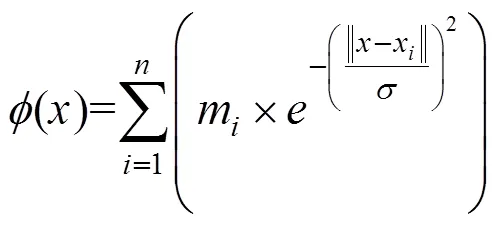
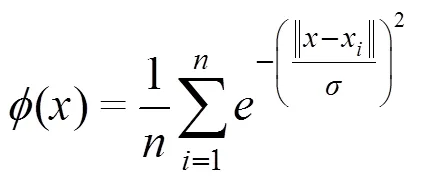
3.2 改进的高斯混合模型聚类流程

基于数据场改进的高斯混合模型隧道施工风险评估的具体步骤如下：

2) 邀请相关领域专家根据施工现场实际情况以及风险等级划分标准对各评价指标进行模糊评语描述；

3) 根据式(1)~(2)对评价指标的模糊评语进行定量转化；

4) 根据式(8)计算每个数据对象x的势值；

5) 画出势值分布图并找到极大值点，设置极大值点个数为聚类个数；

6) 利用高斯混合模型进行聚类分析。

4 工程实例

拉林铁路巴玉隧道位于桑加峡谷区中下游段，隧道进口里程DK190+388，进口段坡度为45°~75°，出口里程 DK203+461，出口段坡度为45°~55°，隧道全长13 073 m，其中单线隧道 12 482 m，双线隧道384 m，三线隧道 207 m，隧道最大埋深约2 080 m。隧址海拔平均高度为3 560 m。线路纵坡为−1.0‰/262 m，−9.8‰/1 190 m，−10.2‰/9 740 m，−6‰/1 450 m和0/431 m的单坡面。加桑峡谷气候干旱少雨，年平均气温 8.8 ℃，极端最低气温−17.6 ℃，极端最高气温29 ℃，年最大雨量 705.7 mm，最大积雪厚度12 cm，冻土厚度16 cm。工程区岩性单一，地层以花岗岩、闪长岩等坚硬岩石为主，地质构造复杂，存在岩爆、地热、放射性、危岩落石以及冻害等不良地质[18]。

4.1 指标评语的转化

本文假定各风险之间相互独立，即在不考虑某一确定风险因素被其他风险因素影响的前提下，专家依据评语集={微小、较小、一般、较大、重大}对指标进行选择评价，对收集到的10位专家评语做统计分析，结果如表5所示。

R44h4,h3h4,h3h4,h4h4,h2h5,h3h4,h3h5,h3h3,h3h3,h4h5,h4 R51h4,h4h4,h3h3,h4h4,h3h2,h4h2,h3h3,h3h2,h4h4,h4h3,h4 R52h4,h4h3,h4h3,h3h2,h4h4,h4h4,h3h2,h4h2,h5h4,h3h3,h2 R53h3,h3h4,h2h3,h4h2,h5h4,h3h2,h4h3,h4h3,h4h3,h4h2,h4 R54h1,h4h2,h3h2,h4h1,h4h1,h5h2,h4h1,h4h1,h4h2,h3h2,h4 R61h5,h4h4,h4h5,h5h5,h4h3,h5h4,h4h5,h5h5,h4h5,h4h3,h4 R62h1,h4h2,h4h2,h4h1,h5h1,h4h2,h3h2,h4h2,h3h1,h3h1,h4 R63h5,h4h4,h3h5,h3h4,h4h3,h5h4,h3h5,h3h5,h4h3,h4h4,h4 R64h4,h4h3,h4h3,h5h4,h4h3,h5h4,h3h3,h4h4,h4h4,h3h3,h4 R65h3,h5h4,h4h3,h5h3,h4h3,h5h4,h4h5,h4h4,h4h3,h4h4,h4 R66h2,h4h2,h4h2,h3h3,h4h3,h3h2,h4h2,h3h3,h4h2,h2h3,h2 R67h2,h4h3,h4h2,h5h3,h4h3,h5h2,h4h2,h5h3,h4h3,h4h2,h5 R68h3,h4h2,h4h2,h5h3,h5h3,h4h4,h5h3,h5h2,h4h2,h4h3,h5

依据式(1)~(2)对表5中的指标模糊评语描述进行定量转化，得到的结果如表6所示。

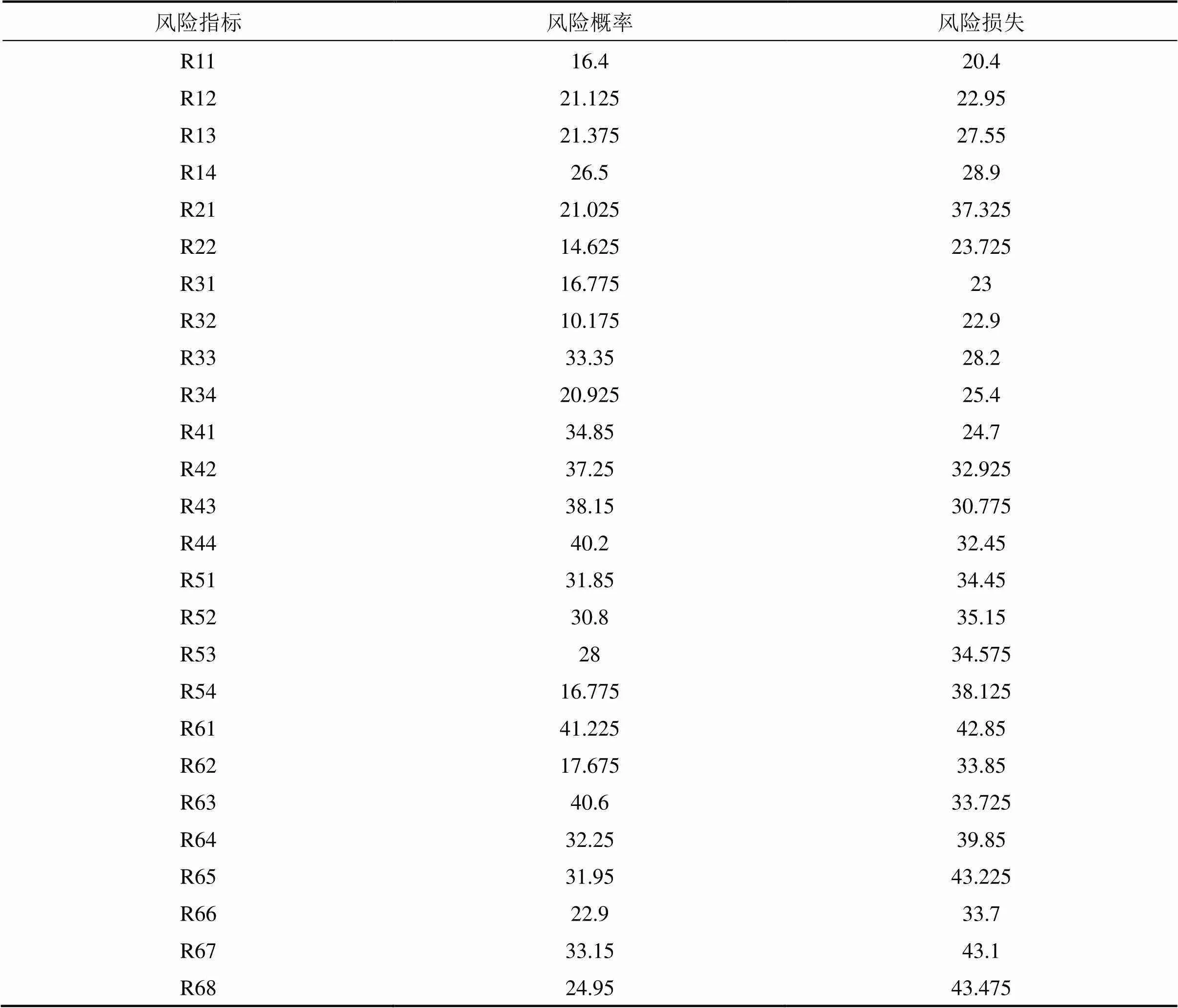
表6 指标评语转化成果

4.2 基于数据场的高斯混合模型聚类结果

按照前述的势值计算方法运用Matlab计算样本势值，得到如图1所示势值分布图。

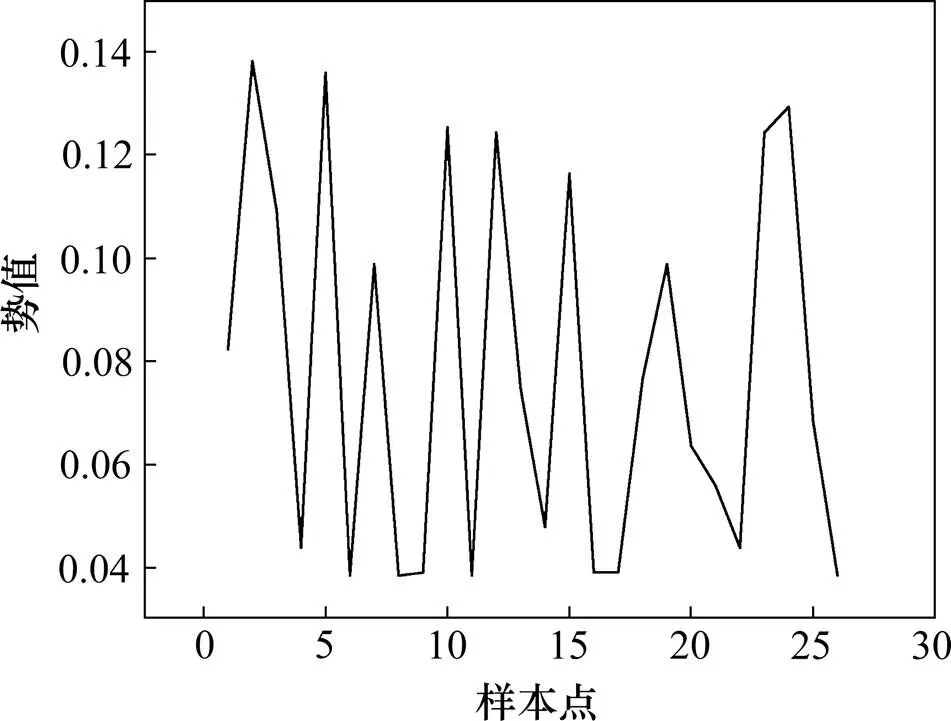
图1 势值分布图

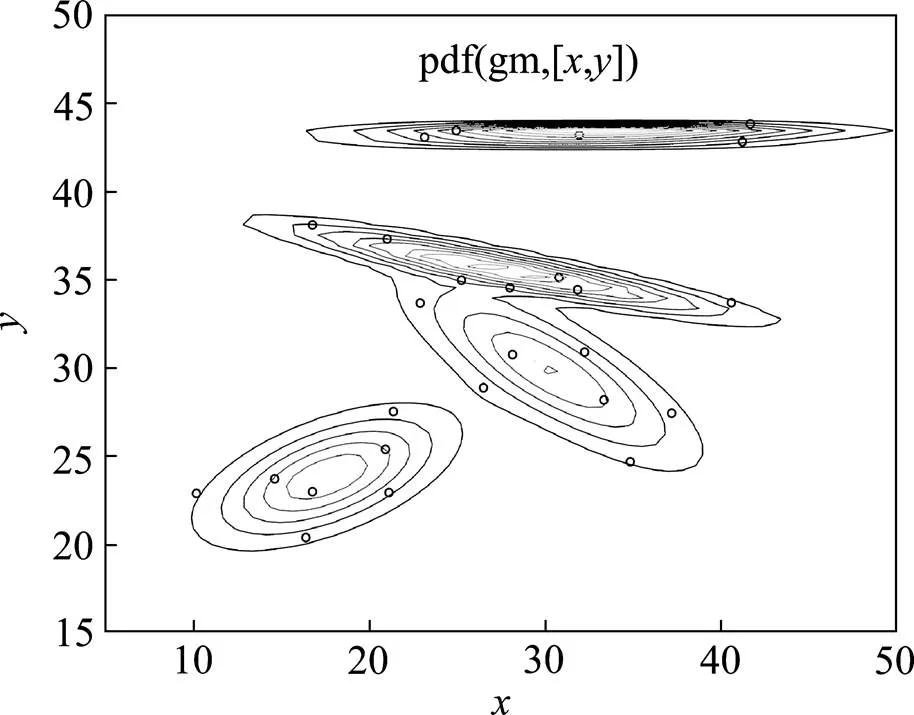
图2 高斯混合聚类图

由图1可以看出有4类极大值，因此初始数据样本有3个聚类中心，可将样本所属风险分为4个等级，在Matlab中运用高斯混合模型进行聚类分析多次运行后得出完整的聚类结果图，结果如图2所示，其中轴为风险概率，轴为风险损失。

为更好地体现出改进后的高斯混合模型聚类优势，将其与传统K-means聚类方法结果进行对比，K-means聚类结果如图3所示。

两者输出聚类结果如表7和表8所示。

由以上分析比较可见，基于数据场的高斯混合模型聚类结果准确性明显高于传统的 K-means聚类。从以上风险分级结果可看出，工程地质风险因素中的岩爆，活动断裂以及高地温等风险都属于重大风险，隧道自然坡度，埋深，危岩落石等固有风险，以及施工过程中易产生有害气体、放射性物质等施工作业环境风险均属于较大风险，这也与巴玉隧道地应力大，岩石坚硬，易发生岩爆；地温高，易产生有害气体等地质特点相吻合，且这些地质特点不利于钻爆等施工作业。为应对岩爆风险，可以循环采取爆破—静止—掘进的施工方法进行作业，在开挖面经常洒冷水或钻孔高压注水以改善围岩物理力学性能；为应对高地温风险，施工时可在隧道衬砌内设计耐高温绝缘隔热材料，并做好施工过程中的通风工作；针对施工过程中无法绕避的滑坡崩塌和活动断裂区需要开展专题研究工作，进行稳定性评价，给出合理的处理意见；施工过程中施工机械保养与警示不足带来的风险属于一般风险，在施工过程中要做好施工前的机械检查工作；相对来说，在此隧道施工过程中，存在安全管理不完善和基础支护工作不足等风险较小，由于围岩多为坚硬岩石，发生软岩大变形的风险也较小，与实际工程情况相符。

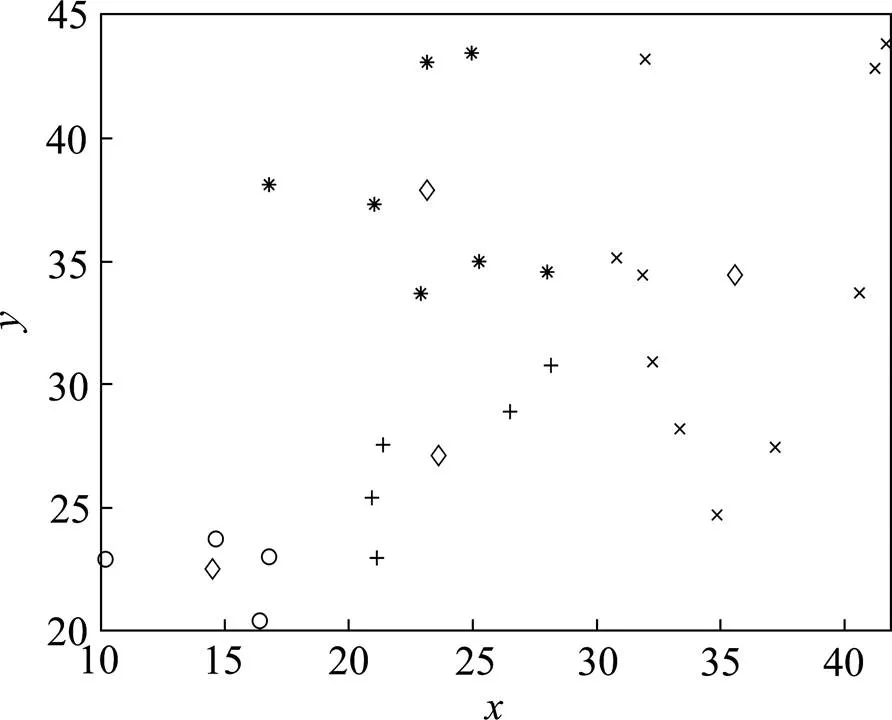
图3 K-means聚类结果图

表7 高斯混合模型聚类输出结果

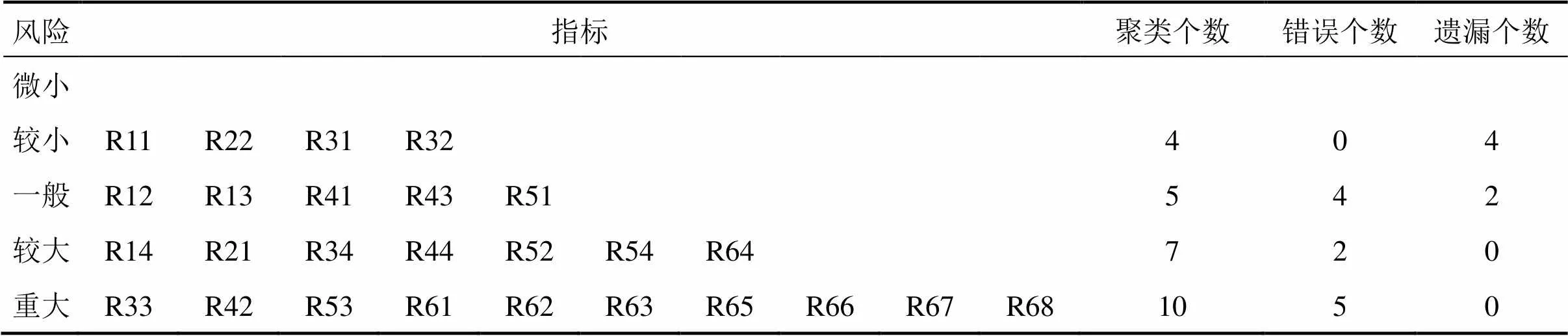
表8 K-means聚类输出结果

5 结论

1) 根据拉林铁路独特的高寒区气候与地质环境，结合铁路隧道施工主要特点，对拉林铁路展开项目风险识别，确定项目中潜在的基本风险事件，较为准确、全面地反映了隧道施工风险系统的结构；运用模糊评语集对隧道施工风险进行描述，并根据经验和阅历赋予被调查专家相应的权重，很大程度上降低了专家打分的主观随意性；最后采用基于数据场改进的高斯混合模型对各风险指标进行聚类分析，得到较为准确的评价结果，为拉林铁路隧道施工风险研究提供一定的参考。

2) 在建立风险指标体系时，虽较为全面的考虑了隧道自身特点和管理、机械、环境以及地质风险因素，但并不能保证各项风险指标之间的独立性，因此后续可以进一步考察各指标之间的相互影响程度以及携带信息熵的重叠程度，提高风险评价体系的可靠性。

3) 相比传统聚类算法，本文采用的基于数据场的高斯混合模型聚类具有计算原理科学，计算步骤简洁以及计算结果准确的优点。但是在计算势值的过程中需要预先设定影响因子的值，如何确定使算法更加完善，是后续可以进行研究的方向。

[1] 宋章, 张广泽, 蒋良文, 等. 川藏铁路主要地质灾害特征及地质选线探析[J]. 铁道标准设计, 2016, 60(1): 14− 19. SONG Zhang, ZHANG Guangze, JIANG Liangwen, et al. The main geological disaster characteristics and geological route selection of Sichuan-Tibet Railway[J]. Railway Standard Design, 2016, 60(1): 14−19.

[2] 杨德宏. 川藏铁路昌都至林芝段主要工程地质问题分析[J/OL]. 铁道标准设计: 1−8 [2019−07−18]. YANG Dehong. Analysis of main engineering geological problems in Changdu-Linzhi section of Sichuan-Tibet railway[J/OL]. Railway Standard Design: 1−8 [2019− 07−18].

[3] 张东明, 白永杰, 白鑫, 等. 深埋长隧道施工地质灾害风险模糊层次评价[J]. 安全与环境学报, 2018, 18(1): 50−55. ZHANG Dongming, BAI Yongjie, BAI Xin, et al. Fuzzy hierarchical assessment of geological disaster risk in deep-buried long tunnel construction[J]. Journal of Safety and Environment, 2018, 18(1): 50−55.

[4] 顾伟红, 王恩茂, 张文达. 铁路隧道TBM施工风险评估[J]. 安全与环境学报, 2018, 18(3): 843−848. GU Weihong, WANG Enmao, ZHANG Wenda. Risk assessment of TBM construction for railway tunnels[J]. Journal of Safety and Environment, 2018, 18(3): 843− 848.

[5] 郭发蔚, 王宏辉. 基于Bayesian隧道施工风险模糊综合评估方法[J]. 铁道科学与工程学报, 2016, 13(2): 401−406. GUO Fawei, WANG Honghui. Fuzzy comprehensive evaluation method based on Bayesian tunnel construction risk[J]. Journal of Railway Science and Engineering, 2016, 13(2): 401−406.

[6] 魏利伟, 王峰, 张强. 青藏高原典型隧道施工安全风险评价研究[J]. 价值工程, 2019, 38(16): 42−45. WEI Liwei, WANG Feng, ZHANG Qiang. Study on the risk assessment of typical tunnel construction in Qinghai- Tibet plateau[J]. Value Engineering, 2019, 38(16): 42−45.

[7] 李德毅, 刘常昱, 杜鹢, 等. 不确定性人工智能[J]. 软件学报, 2004(11): 1583−1594. LI Deyi, LIU Changyu, DU Yu, et al. Uncertainty artificial intelligence[J]. Journal of Software, 2004(11): 1583−1594.

[8] 李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J].计算机研究与发展, 1995(6): 15−20. LI Deyi, MENG Haijun, SHI Xuemei. Subordinate cloud and subordinate cloud generator[J]. Computer Research and Development, 1995(6): 15−20.

[9] 张敏, 张广泽, 蒋良文, 等. 川藏铁路雅鲁藏布江缝合带地质选线研究[J]. 资源信息与工程, 2019, 34(1): 164−166. ZHANG Min, ZHANG Guangze, JIANG Liangwen, et al. Study on geological line selection of Yarlung Zangbo River suture zone on Sichuan-Tibet Railway[J]. Resource Information and Engineering, 2019, 34(1): 164−166.

[10] TZ 204—2008, 铁路隧道工程施工技术指南[S]. TZ 204—2008, Guidelines for construction technology of railway tunnel engineering[S].

[11] 郭长宝, 张永双, 蒋良文, 等. 川藏铁路沿线及邻区环境工程地质问题概论[J]. 现代地质, 2017, 31(5): 877− 889. GUO Changbao, ZHANG Yongshuang, JIANG Liangwen, et al. An Introduction of environmental engineering geological problems among Sichuan-Tibet Railway and its Adjacent Areas[J]. Modern Geology, 2017, 31(5): 877−889.

[12] 王华牢, 李宁, 王皓. 隧道施工塌方风险评估与控制措施[J]. 交通运输工程学报, 2010, 10(4): 34−38. WANG Hualao, LI Ning, WANG Hao. Risk assessment and control measures of tunnel collapse[J]. Journal of Transportation Engineering, 2010, 10(4): 34−38.

[13] Gionis A, Mannila H, Tsaparas P. Clustering aggregation [J]. Acm Transactions on Knowledge Discovery from Data, 2005, 1(1): 4.

[14] 陈英. 高斯混合模型聚类及其优化算法研究[D]. 南昌: 华东交通大学, 2015.CHEN Ying. Clustering of Gauss mixture model and its optimal algorithms[D]. Nanchang: East China Jiaotong University, 2015.

[15] 任恒妮. 大数据K-means聚类算法的研究与应用[J]. 信息技术, 2019, 43(11): 20−23. REN Hengni. Research and application of K-means clustering algorithm for big data[J]. Information Technology, 2019, 43(11): 20−23.

[16] WANG S, WANG D, LI Caoyuan , et al. Clustering by fast search and find of density peaks with data field[J]. Chinese Journal of Electronics, 2016, 25(3): 397−402.

[17] 陈玉雯. 基于高斯混合模型聚类的变量选择及应用[D]. 兰州: 兰州大学, 2016. CHEN Yuwen. Variable selection and application based on Gauss mixture model clustering[D]. Lanzhou: Lanzhou University, 2016.

[18] 王栋, 李天斌, 蒋良文, 等. 川藏铁路某超深埋隧道地应力特征及岩爆分析[J]. 铁道工程学报, 2017, 34(4): 46−50. WANG Dong, LI Tianbin, JIANG Liangwen, et al. In-situ stress characteristics and rockburst analysis of an ultra-deep tunnel on Sichuan-Tibet Railway[J]. Journal of Railway Engineering, 2017, 34(4): 46−50.

Construction risk assessment of Lhasa-Linzhi railway tunnel based on data field clustering

ZHANG Huan, HAO Wei,GU Weihong

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to clarify the risk level of complex construction environment and harsh climate conditions for Lhasa-Linzhi Railway tunnel construction in alpine region, a tunnel construction risk assessment model based on data field clustering was proposed. According to the construction characteristics of tunnel engineering in Lhasa-Linzhi Railway, the main Construction risk and inherent risk of tunnel construction were analyzed, and the risk evaluation index system of tunnel construction in line with the geological characteristics of Lhasa-Linzhi Railway was constructed. The risk probability and risk loss of risk indicators were described by using fuzzy comment set. After quantitative transformation of the description results, the risk factors were classified by Gaussian mixture model clustering based on data field. Finally, the construction risk of Bayu tunnel in Lhasa-Linzhi Railway was evaluated by using the model, and compared the result with the traditional K-means clustering method. The study is proved that the evaluation results of Gaussian mixture model are more accurate.

Lhasa-Linzhi Railway; tunnel construction; construction safety; data field; cluster analysis; Gauss mixture model

10.19713/j.cnki.43−1423/u.T20190855

U45

A

1672 − 7029(2020)07 − 1874 − 09

2019−09−23

长江学者和创新团队发展计划滚动资助项目(IRT-15R29)；国家自然科学基金资助项目(51668037)

郝伟(1968−)，女，甘肃兰州人，副教授，从事建设工程项目管理及经济评价研究；E−mail：862535923@qq.com

(编辑 蒋学东)